Q-Faktor und Bandbreite eines Resonanzkreises

Der Q- oder Qualitätsfaktor eines Schwingkreises ist ein Maß für die „Güte“ oder Qualität eines Schwingkreises. Ein höherer Wert für diese Gütezahl entspricht einer schmaleren Bandbreite, die in vielen Anwendungen wünschenswert ist. Formaler ausgedrückt ist Q das Verhältnis von gespeicherter Leistung zu Verlustleistung in der Reaktanz bzw. dem Widerstand der Schaltung:

Q =Pgespeichert /Pverloren =I
2
 X/I
2
 R Q =X/R wobei:X =Kapazitive oder induktive Reaktanz bei Resonanz R =Serienwiderstand. 

Diese Formel gilt für Serienresonanzkreise und auch für Parallelresonanzkreise, wenn der Widerstand in Reihe mit der Induktivität liegt. Dies ist in praktischen Anwendungen der Fall, da es sich hauptsächlich um den Widerstand der Induktivität handelt, der den Q begrenzt.

Hinweis: Einige Texte zeigen möglicherweise, dass X und R in der „Q“-Formel für einen Parallelschwingkreis vertauscht sind. Dies ist richtig für einen großen Wert von R parallel zu C und L. Unsere Formel ist richtig für ein kleines R in Reihe mit L.

Eine praktische Anwendung von „Q“ besteht darin, dass die Spannung über L oder C in einem Serienresonanzkreis das Q-fache der gesamten angelegten Spannung beträgt. In einem Parallelschwingkreis ist der Strom durch L oder C das Q-fache des gesamten angelegten Stroms.

Serien-Resonanzkreise

Ein Reihenschwingkreis sieht bei der Resonanzfrequenz wie ein Widerstand aus. Da die Definition von Resonanz X_L . ist =X_C , heben sich die reaktiven Komponenten auf, sodass nur der Widerstand zur Impedanz beiträgt.

Die Impedanz ist auch bei Resonanz minimal. Unterhalb der Resonanzfrequenz sieht der Serienresonanzkreis kapazitiv aus, da die Impedanz des Kondensators auf einen Wert größer als die abnehmende induktive Reaktanz ansteigt, wodurch ein kapazitiver Nettowert verbleibt.

Oberhalb der Resonanz erhöht sich die induktive Reaktanz, die kapazitive Reaktanz nimmt ab und hinterlässt eine induktive Nettokomponente.

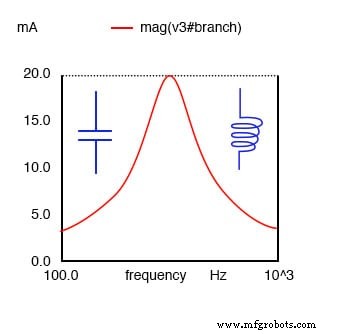
HINWEIS:

Bei Resonanz erscheint der Serienresonanzkreis rein ohmsch. Unterhalb der Resonanz sieht es kapazitiv aus. Oberhalb der Resonanz erscheint es induktiv. Der Strom ist bei Resonanz maximal, die Impedanz minimal. Der Strom wird durch den Widerstandswert eingestellt. Über oder unter der Resonanz steigt die Impedanz.

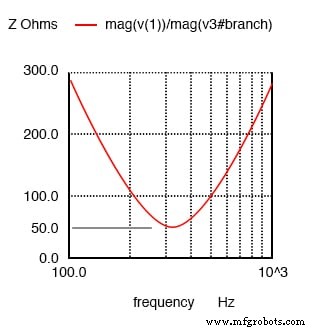
Impedanz ist bei Resonanz in einem Serienresonanzkreis minimal.

Die Resonanzstromspitze kann durch Variieren des Reihenwiderstands verändert werden, was den Q-Wert verändert. Dies beeinflusst auch die Breite der Kurve. Eine Schaltung mit niedrigem Widerstand und hohem Q hat eine schmale Bandbreite im Vergleich zu einer Schaltung mit hohem Widerstand und niedrigem Q.

Bandbreite in Bezug auf Q und Resonanzfrequenz:

 BW =fc /Q Wobei fc =Resonanzfrequenz Q =Gütefaktor

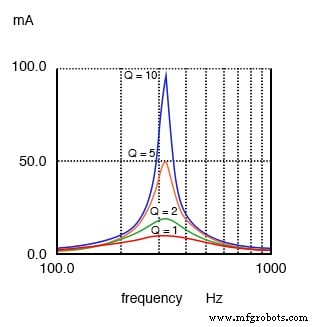
Ein Resonanzkreis mit hohem Q hat eine schmale Bandbreite im Vergleich zu einem niedrigen Q

Die Bandbreite wird zwischen den 0,707 Stromamplitudenpunkten gemessen. Die 0,707 Strompunkte entsprechen den halben Leistungspunkten, da P =I ² R, (0.707) ² =(0.5).

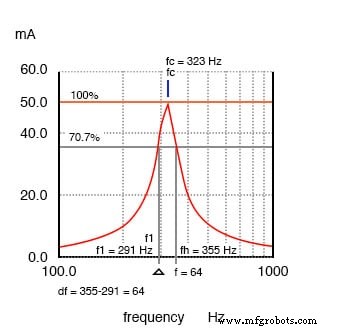
Bandbreite, Δf wird zwischen den 70,7% Amplitudenpunkten des Serienresonanzkreises gemessen.

 BW =Δf =fh -fl =fc /Q Wobei:fh =hohe Bandkante fl =untere Bandkante fl =fc - Δf/2 fh =fc + Δf/2 Wobei fc =Mittenfrequenz (Resonanzfrequenz)

In der obigen Abbildung beträgt der 100%-Strompunkt 50 mA. Der 70,7 %-Wert beträgt 0,707 (50 mA) =35,4 mA. Die aus der Kurve abgelesenen oberen und unteren Bandkanten betragen 291 Hz für fl und 355 Hz für f_h . Die Bandbreite beträgt 64 Hz und die Halbwertspunkte liegen bei ± 32 Hz der Mittenresonanzfrequenz:

 BW =Δf =fh -fl =355-291 =64 fl =fc - Δf/2 =323-32 =291 fh =fc + Δf/2 =323+32 =355

Da BW =fc/Q:

Q =f_c /BW =(323 Hz)/(64 Hz) =5

Parallele Resonanzkreise

Die Impedanz eines Parallelschwingkreises ist bei der Resonanzfrequenz maximal. Unterhalb der Resonanzfrequenz sieht der Parallelschwingkreis induktiv aus, da die Impedanz der Induktivität niedriger ist und den größeren Stromanteil zieht.

Oberhalb der Resonanz nimmt die kapazitive Reaktanz ab, zieht den größeren Strom und nimmt somit eine kapazitive Charakteristik an.

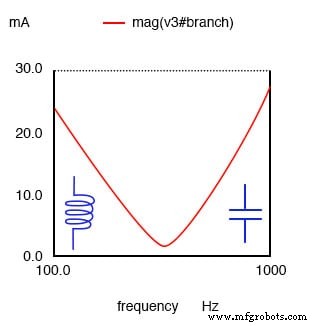
Ein Parallelschwingkreis ist bei Resonanz ohmsch, unterhalb der Resonanz induktiv, oberhalb der Resonanz kapazitiv.

Die Impedanz ist bei Resonanz in einem Parallelschwingkreis maximal, nimmt jedoch oberhalb oder unterhalb der Resonanz ab. Die Spannung hat bei Resonanz einen Spitzenwert, da die Spannung proportional zur Impedanz ist (E=IZ).

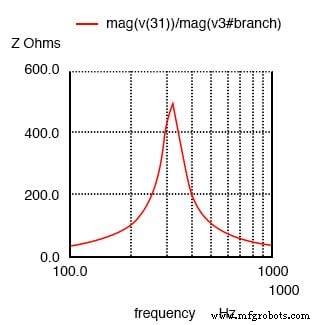
Parallelschwingkreis:Impedanzspitzen bei Resonanz.

Ein niedriger Q aufgrund eines hohen Widerstands in Reihe mit der Induktivität erzeugt eine niedrige Spitze auf einer breiten Ansprechkurve für einen Parallelschwingkreis. Ein hoher Q ist auf einen niedrigen Widerstand in Reihe mit der Induktivität zurückzuführen. Dies erzeugt einen höheren Peak in der schmaleren Ansprechkurve. Der hohe Q wird erreicht, indem der Induktor mit einem Draht mit größerem Durchmesser (kleinere Dicke) und niedrigerem Widerstand gewickelt wird.

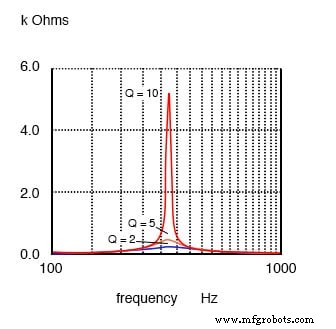
Die parallele Resonanzantwort variiert mit Q.

Die Bandbreite der parallelen Resonanzkurve wird zwischen den Halbleistungspunkten gemessen. Dies entspricht den 70,7 % Spannungspunkten, da die Leistung proportional zu E ² . ist . ((0.707) ² =0.50) Da die Spannung proportional zur Impedanz ist, können wir die Impedanzkurve verwenden.

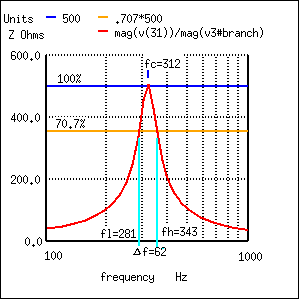
Bandbreite, Δf wird zwischen den 70,7% Impedanzpunkten eines Parallelschwingkreises gemessen.

In der obigen Abbildung beträgt der 100%-Impedanzpunkt 500 . Der Wert von 70,7 % beträgt 0707(500)=354 Ω. Die aus der Kurve abgelesenen oberen und unteren Bandkanten betragen 281 Hz für fl und 343 Hz für fh. Die Bandbreite beträgt 62 Hz und die Halbwertspunkte liegen bei ± 31 Hz der Mittenresonanzfrequenz:

BW =Δf =fh -fl =343-281 =62 fl =fc - f/2 =312-31 =281 fh =fc + Δf/2 =312+31 =343

Q =fc/BW =(312 Hz)/(62 Hz) =5

VERWANDTE ARBEITSBLÄTTER:

• Resonanz-Arbeitsblatt
• Arbeitsblatt zur algebraischen Substitution von Stromkreisen