Frequenz- und Phasenmessung

Eine wichtige elektrische Größe ohne Äquivalent in Gleichstromkreisen ist die Frequenz .

Die Frequenzmessung ist in vielen Wechselstromanwendungen sehr wichtig, insbesondere in Wechselstromsystemen, die für einen effizienten Betrieb mit einer Frequenz und nur einer Frequenz ausgelegt sind.

Wenn der Wechselstrom von einem elektromechanischen Generator erzeugt wird, ist die Frequenz direkt proportional zur Wellendrehzahl der Maschine, und die Frequenz könnte einfach durch Messen der Wellendrehzahl gemessen werden.

Wenn die Frequenz jedoch in einiger Entfernung von der Lichtmaschine gemessen werden muss, sind andere Messmethoden erforderlich.

Methode der Frequenzmessung

Mit dem Prinzip der mechanischen Resonanz

Eine einfache, aber grobe Methode zur Frequenzmessung in Energiesystemen verwendet das Prinzip der mechanischen Resonanz. Jedes physikalische Objekt mit der Eigenschaft der Elastizität (Federbarkeit) hat eine Eigenfrequenz, bei der es bevorzugt schwingt.

Die Stimmgabel ist ein großartiges Beispiel dafür:Wenn Sie einmal darauf schlagen, vibriert sie weiter mit einem für ihre Länge spezifischen Ton. Längere Stimmgabeln haben niedrigere Resonanzfrequenzen:Ihre Töne sind auf der Tonleiter tiefer als kürzere Stimmgabeln.

Stellen Sie sich eine Reihe von Stimmgabeln in progressiver Größe vor, die nebeneinander angeordnet sind. Sie sind alle auf einem gemeinsamen Sockel montiert, und dieser Sockel wird mittels eines Elektromagneten mit der Frequenz der gemessenen Wechselspannung (oder des gemessenen Stroms) in Schwingung versetzt.

Welche Stimmgabel in der Resonanzfrequenz der Frequenz dieser Schwingung am nächsten ist, neigt dazu, am stärksten (oder am lautesten) zu zittern. Wenn die Zinken der Gabeln dünn genug wären, könnten wir die relative Bewegung der einzelnen Gabeln anhand der Länge der Unschärfe sehen, die wir sehen würden, wenn wir jede einzelne aus der Endansichtsperspektive inspizieren.

Nun, machen Sie eine Sammlung von "Stimmgabeln" aus einem Blechstreifen, der in einem Muster ähnlich einem Rechen geschnitten ist, und Sie haben das vibrierende Blatt Frequenzmesser:

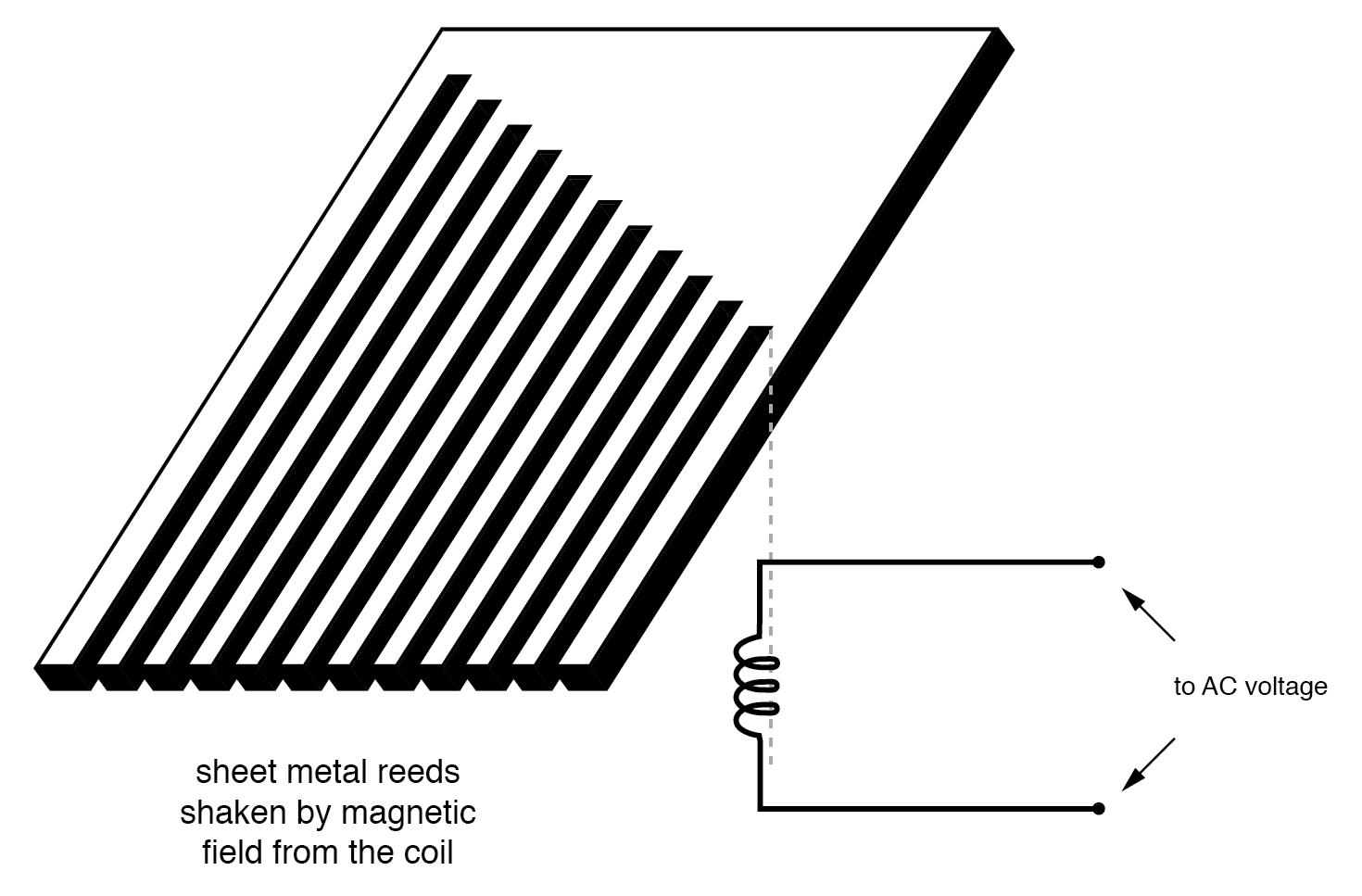
Vibrierendes Zungenfrequenzmesser-Diagramm.

Der Benutzer dieses Messgeräts betrachtet die Enden all dieser Zungen mit ungleicher Länge, während sie gemeinsam mit der Frequenz der an die Spule angelegten Wechselspannung geschüttelt werden. Diejenige, die der angelegten Wechselspannung in der Resonanzfrequenz am nächsten ist, vibriert am stärksten und sieht in etwa so aus:

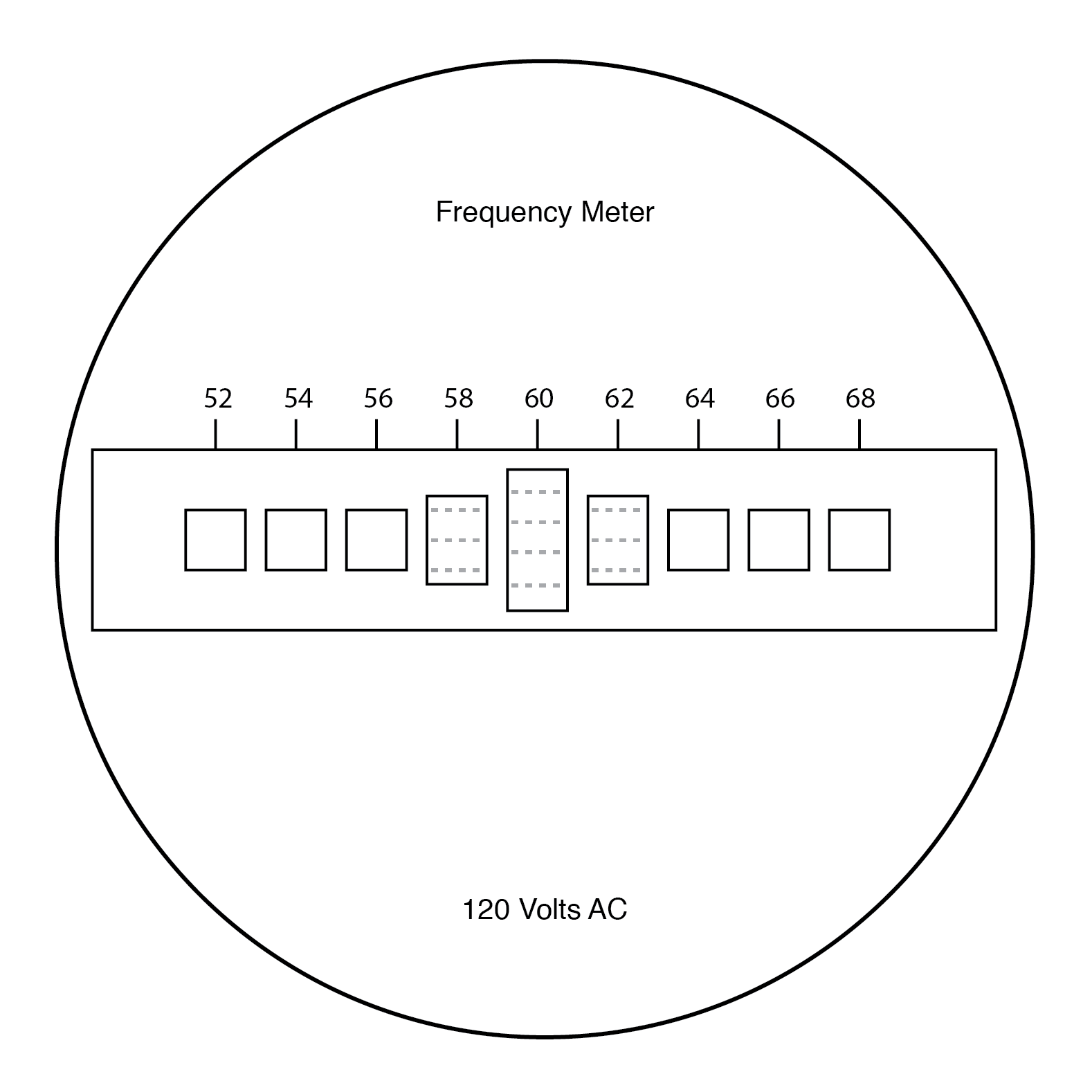
Vibrierende Zungenfrequenzmesser-Frontplatte.

Schwingblattmesser sind natürlich keine Präzisionsinstrumente, aber sie sind sehr einfach und daher leicht herzustellen, um robust zu sein. Sie werden oft an kleinen motorbetriebenen Generatorsätzen gefunden, um die Motordrehzahl so einzustellen, dass die Frequenz ungefähr 60 (50 in Europa) Hertz beträgt.

Eine Form von Tank Circuit verwenden

Reed-Messgeräte sind zwar ungenau, ihr Funktionsprinzip jedoch nicht. Anstelle von mechanischer Resonanz können wir elektrische Resonanz ersetzen und einen Frequenzmesser mit einer Induktivität und einem Kondensator in Form eines Schwingkreises (Parallelinduktivität und Kondensator) konstruieren. Siehe Abbildung unten.

Eine oder beide Komponenten sind einstellbar, und ein Messgerät wird in den Stromkreis eingefügt, um die maximale Amplitude der Spannung zwischen den beiden Komponenten anzuzeigen.

Die Einstellknöpfe sind so kalibriert, dass sie die Resonanzfrequenz für jede gegebene Einstellung anzeigen, und die Frequenz wird von ihnen abgelesen, nachdem das Gerät für die maximale Anzeige auf dem Messgerät eingestellt wurde.

Im Wesentlichen handelt es sich um eine abstimmbare Filterschaltung, die ähnlich einer Brückenschaltung eingestellt und dann gelesen wird (die für einen „Null“-Zustand abgeglichen und dann gelesen werden muss).

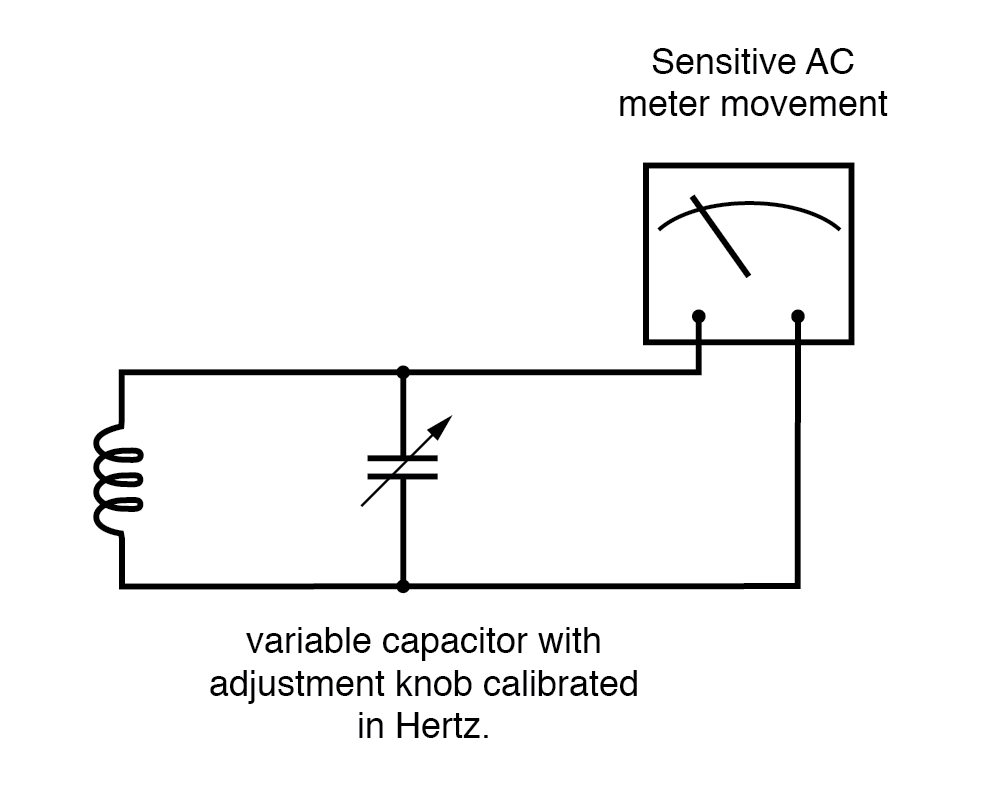
Resonanzfrequenzmesser "spitzen", wenn die L-C-Resonanzfrequenz auf die Testfrequenz abgestimmt ist.

Diese Technik ist bei Amateurfunkern beliebt (oder zumindest vor dem Aufkommen kostengünstiger digitaler Frequenzinstrumente namens Zähler ), vor allem, weil keine direkte Verbindung zum Stromkreis erforderlich ist.

Solange die Induktivität und/oder der Kondensator genügend Streufeld (magnetisch bzw. elektrisch) vom zu prüfenden Stromkreis abfangen können, um eine Anzeige des Messgeräts zu bewirken, funktioniert es.

Bei der Frequenz wie bei anderen Arten der elektrischen Messung sind die genauesten Messmethoden normalerweise diejenigen, bei denen eine unbekannte Größe mit einem bekannten Standard verglichen wird , das Grundinstrument, das nichts weiter tut, als anzuzeigen, wann die beiden Größen einander gleich sind.

Dies ist das Grundprinzip der DC (Wheatstone)-Brückenschaltung und ein solides messtechnisches Prinzip, das in allen Wissenschaften angewendet wird. Wenn wir Zugang zu einem genauen Frequenznormal haben (eine Wechselspannungsquelle, die sehr genau auf einer einzelnen Frequenz hält), sollte die Messung einer unbekannten Frequenz im Vergleich relativ einfach sein.

Quarzkristall verwenden

Für diesen Frequenzstandard wenden wir unsere Aufmerksamkeit wieder der Stimmgabel oder zumindest einer moderneren Variante davon namens Quarzkristall zu .

Quarz ist ein natürlich vorkommendes Mineral mit einer sehr interessanten Eigenschaft namens Piezoelektrizität . Piezoelektrische Materialien erzeugen bei körperlicher Belastung eine Spannung über ihre Länge und verformen sich physisch, wenn eine externe Spannung über ihre Länge angelegt wird.

Diese Verformung ist in den meisten Fällen sehr, sehr gering, aber sie existiert.

Quarzgestein ist elastisch (federnd) innerhalb des kleinen Biegebereichs, den eine externe Spannung erzeugen würde, was bedeutet, dass es eine eigene mechanische Resonanzfrequenz hat, die sich als elektrisches Spannungssignal manifestieren kann.

Mit anderen Worten, wenn ein Quarzchip angeschlagen wird, "klingelt" er mit seiner eigenen einzigartigen Frequenz, die durch die Länge des Chips bestimmt wird, und diese Resonanzschwingung erzeugt eine äquivalente Spannung an mehreren Punkten des Quarzchips, die abgegriffen werden kann durch Drähte, die an der Oberfläche des Chips befestigt sind.

Umgekehrt neigt der Quarzchip am stärksten zu Schwingungen, wenn er durch eine angelegte Wechselspannung mit genau der richtigen Frequenz „erregt“ wird, genau wie die Zungen eines Schwingblatt-Frequenzmessers.

Quarzsteinsplitter können für die gewünschten Resonanzfrequenzen präzise geschnitten werden, und dieser Chip wird sicher in einer Schutzhülle mit Drähten befestigt, die zum Anschluss an einen externen Stromkreis verlängert werden.

Als solches verpackt wird das resultierende Gerät einfach als Kristall bezeichnet (oder manchmal „xtal “). Das schematische Symbol ist in der folgenden Abbildung dargestellt.

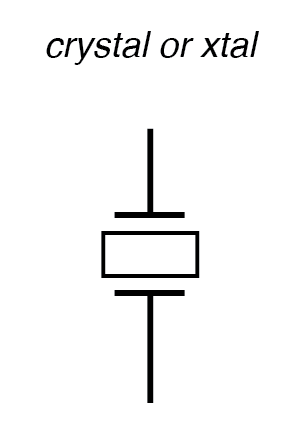
Kristall (frequenzbestimmendes Element) schematisches Symbol.

Elektrisch entspricht dieser Quarzchip einem Reihen-LC-Schwingkreis. (Abbildung unten) Die dielektrischen Eigenschaften von Quarz tragen ein zusätzliches kapazitives Element zum Ersatzschaltbild bei.

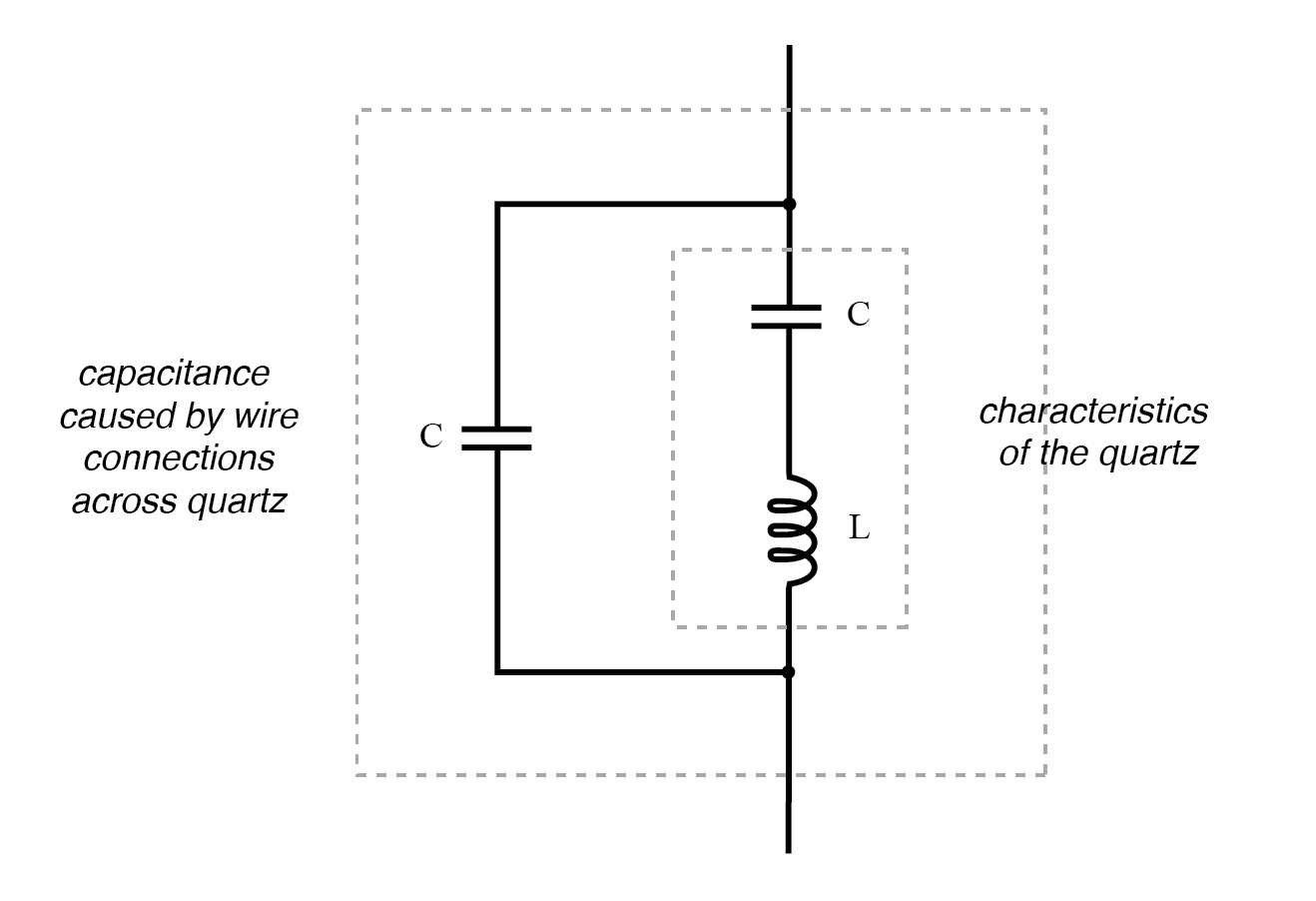
Quarzquarz-Ersatzschaltung.

Die in Reihe gezeigten „Kapazität“ und „Induktivität“ sind lediglich elektrische Äquivalente der mechanischen Resonanzeigenschaften des Quarzes:Sie existieren nicht als diskrete Komponenten innerhalb des Kristalls. Die parallel angezeigte Kapazität aufgrund der Drahtverbindungen über den dielektrischen (isolierenden) Quarzkörper ist real und hat einen Einfluss auf das Resonanzverhalten des gesamten Systems.

Eine vollständige Diskussion der Quarzdynamik ist hier nicht erforderlich, aber was man über Quarze verstehen muss, ist diese Resonanzkreis-Äquivalenz und wie sie innerhalb einer Oszillatorschaltung ausgenutzt werden kann, um eine Ausgangsspannung mit einer stabilen, bekannten Frequenz zu erreichen.

Kristalle haben als Resonanzelemente normalerweise ein viel höheres „Q“ (Qualität )-Werte als Schwingkreise aus Induktivitäten und Kondensatoren, hauptsächlich aufgrund des relativen Fehlens von Streuwiderständen, wodurch ihre Resonanzfrequenzen sehr definiert und präzise sind.

Da die Resonanzfrequenz ausschließlich von den physikalischen Eigenschaften von Quarz (einer mechanisch sehr stabilen Substanz) abhängt, ist die zeitliche Änderung der Resonanzfrequenz bei einem Quarzkristall sehr, sehr gering. So funktioniert Quarzwerk Uhren erhalten ihre hohe Ganggenauigkeit:durch einen elektronischen Oszillator, der durch die Resonanz eines Quarzkristalls stabilisiert wird.

Für Laboranwendungen kann jedoch eine noch größere Frequenzstabilität erwünscht sein. Um dies zu erreichen, kann der fragliche Kristall in eine temperaturstabilisierte Umgebung (normalerweise ein Ofen) gebracht werden, wodurch Frequenzfehler aufgrund von Wärmeausdehnung und -kontraktion des Quarzes eliminiert werden.

Für den ultimativen Frequenzstandard jedoch übertrifft nichts bisher die Genauigkeit eines einzelnen schwingenden Atoms. Dies ist das Prinzip der sogenannten Atomuhr , das ein in einem Vakuum schwebendes Quecksilberatom (oder Cäsiumatom) verwendet, das durch äußere Energie angeregt wird, um mit seiner eigenen einzigartigen Frequenz zu schwingen.

Die resultierende Frequenz wird als Radiowellensignal erfasst und bildet die Grundlage für die genauesten Uhren, die der Menschheit bekannt sind. Nationale Standardlabore auf der ganzen Welt unterhalten einige dieser hochgenauen Uhren und senden Frequenzsignale basierend auf den Schwingungen dieser Atome, damit Wissenschaftler und Techniker sich einstellen und für Frequenzkalibrierungszwecke verwenden können.

Praktischer Teil

Jetzt kommen wir zum praktischen Teil:Sobald wir eine Quelle haben der genauen Frequenz, wie vergleichen wir diese mit einer unbekannten Frequenz, um eine Messung zu erhalten?

Eine Möglichkeit besteht darin, eine CRT als Frequenzvergleichsvorrichtung zu verwenden. Kathodenstrahlröhren haben typischerweise Mittel zum Ablenken des Elektronenstrahls sowohl in der horizontalen als auch in der vertikalen Achse.

Wenn Metallplatten verwendet werden, um die Elektronen elektrostatisch abzulenken, befinden sich links und rechts des Strahls ein Plattenpaar sowie ein Plattenpaar über und unter dem Strahl, wie in der Abbildung unten gezeigt.

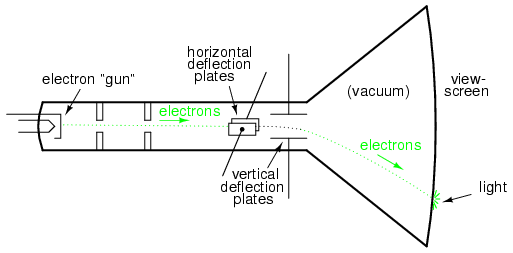
Kathodenstrahlröhre (CRT) mit vertikalen und horizontalen Ablenkplatten.

Wenn wir zulassen, dass ein AC-Signal den Strahl nach oben und unten ablenkt (verbinden Sie diese AC-Spannungsquelle mit den „vertikalen“ Ablenkplatten) und ein anderes AC-Signal den Strahl nach links und rechts ablenken (mit dem anderen Paar Ablenkplatten), werden die Muster auf dem Bildschirm der Kathodenstrahlröhre erzeugt werden, die das Verhältnis angibt dieser beiden Wechselstromfrequenzen.

Diese Muster werden Lissajous-Figuren genannt und sind ein übliches Mittel zur vergleichenden Frequenzmessung in der Elektronik.

Wenn die beiden Frequenzen gleich sind, erhalten wir auf dem Bildschirm der Kathodenstrahlröhre eine einfache Figur, deren Form von der Phasenverschiebung zwischen den beiden Wechselstromsignalen abhängt. Hier ist eine Auswahl von Lissajous-Figuren für zwei Sinuswellensignale gleicher Frequenz, die so dargestellt werden, wie sie auf der Vorderseite eines Oszilloskops (einem Wechselspannungsmessgerät mit einer Kathodenstrahlröhre als „Bewegung“) erscheinen würden.

Das erste Bild zeigt die Lissajous-Figur, die aus zwei perfekt phasengleichen Wechselspannungen besteht:

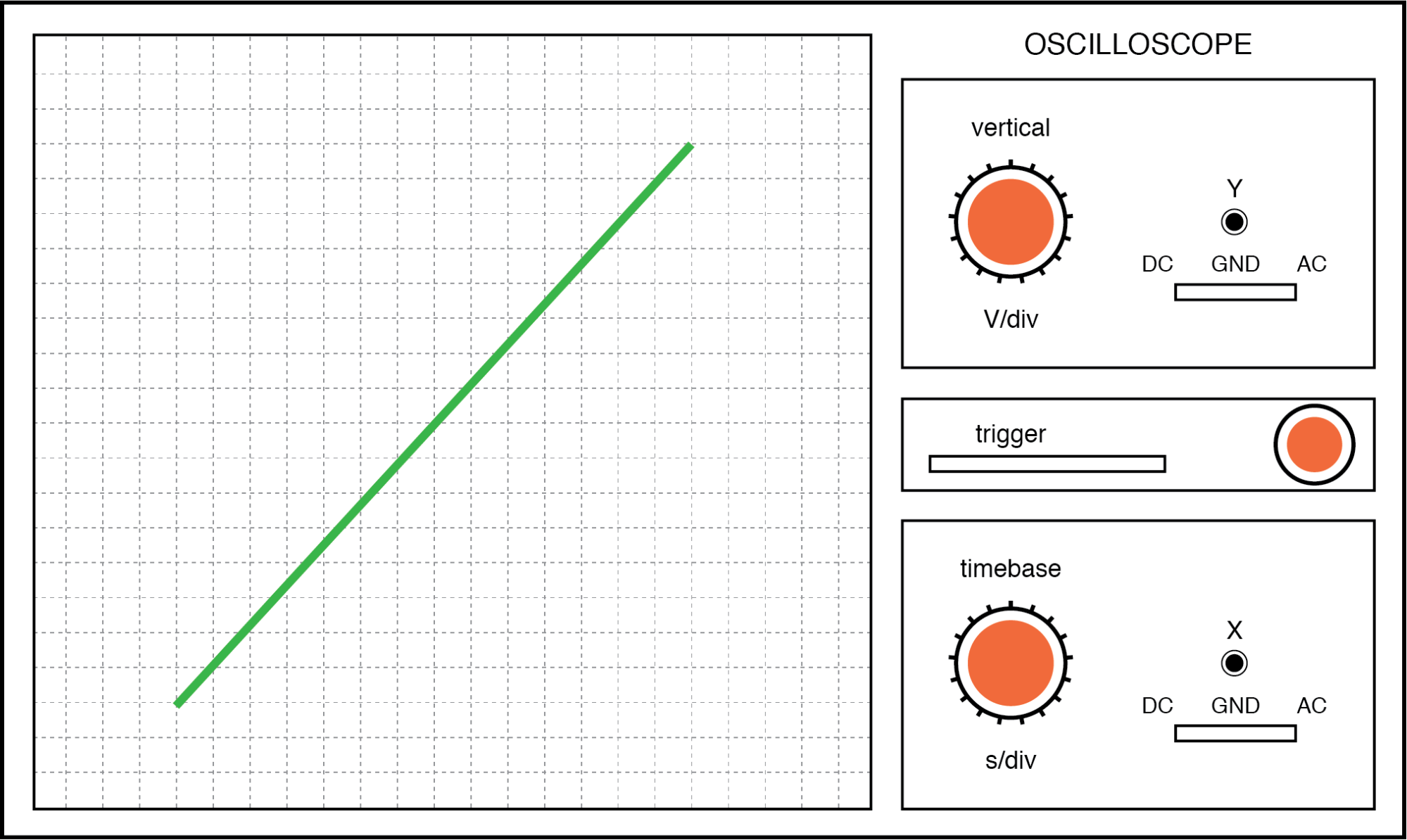
Lissajous-Figur:gleiche Frequenz, null Grad Phasenverschiebung.

Wenn die beiden Wechselspannungen nicht phasengleich sind, wird keine Gerade gebildet. Stattdessen nimmt die Lissajous-Figur das Aussehen eines Ovals an und wird perfekt kreisförmig, wenn die Phasenverschiebung zwischen den beiden Signalen genau 90° beträgt und ihre Amplituden gleich sind:

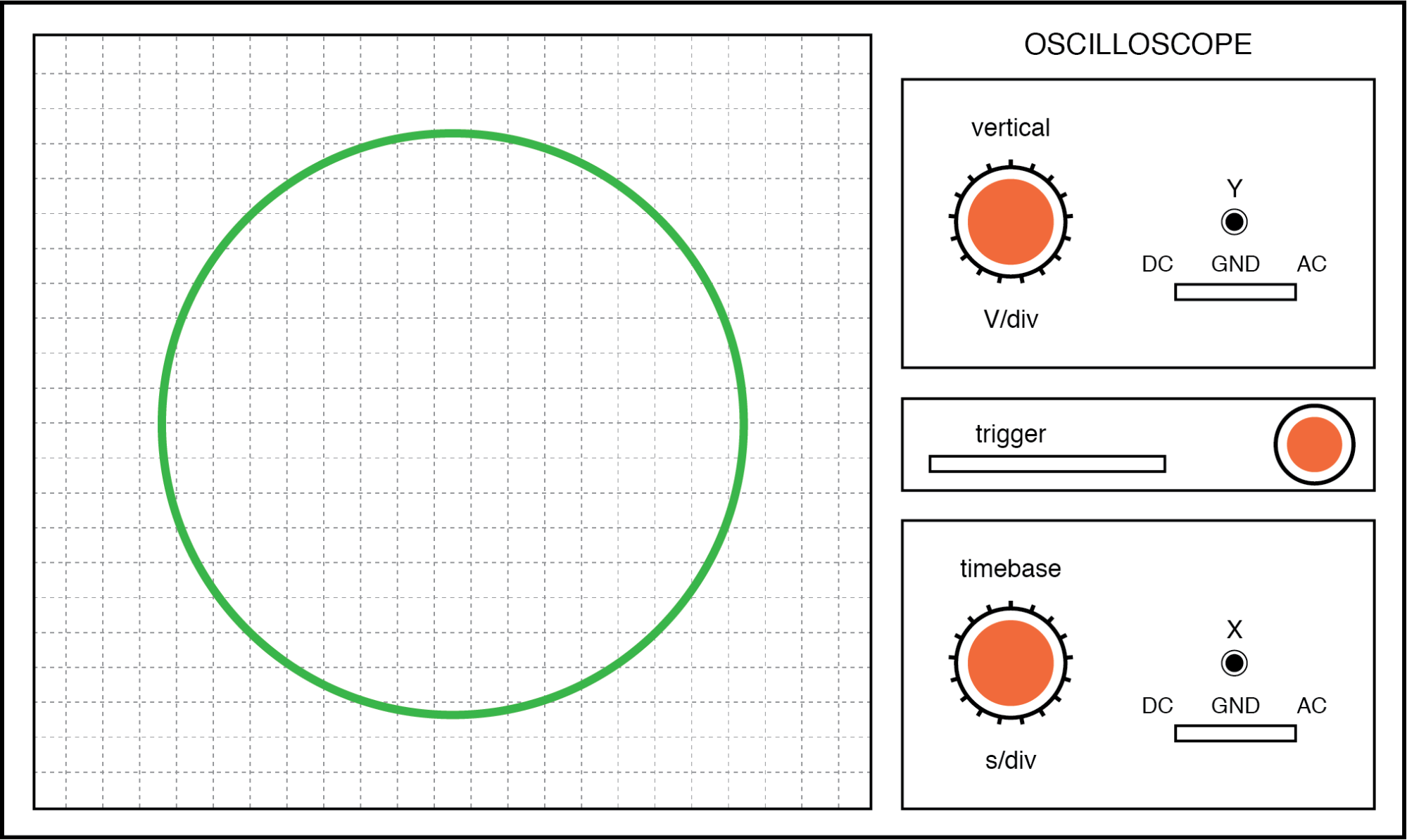
Lissajous-Figur:gleiche Frequenz, 90 oder 270 Grad Phasenverschiebung.

Wenn sich die beiden AC-Signale schließlich in der Phase direkt gegenüberliegen (180°-Verschiebung), erhalten wir wieder eine Linie, nur diesmal ist sie in die entgegengesetzte Richtung ausgerichtet:

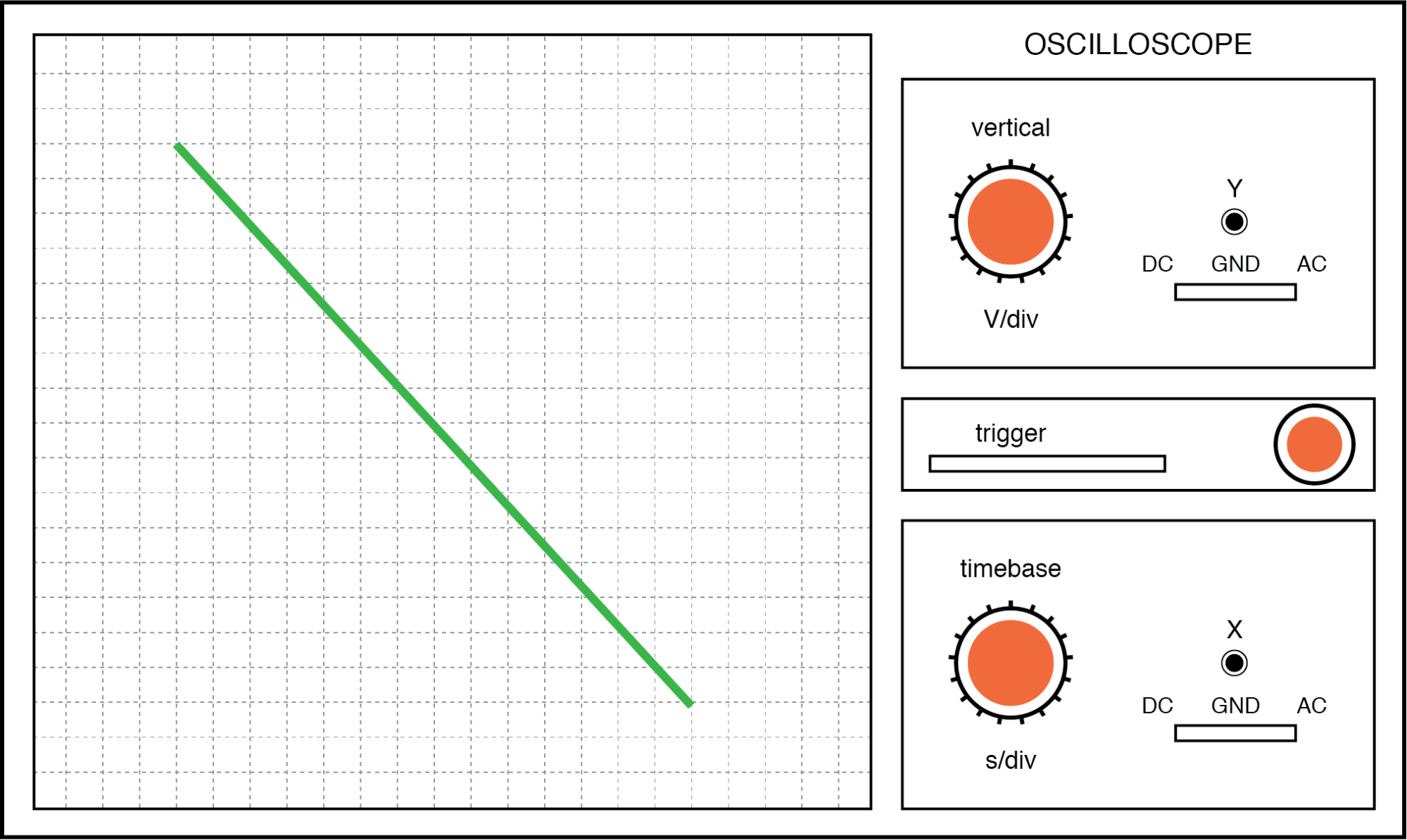
Lissajous-Figur:gleiche Frequenz, 180 Grad Phasenverschiebung.

Wenn wir mit Signalfrequenzen konfrontiert werden, die nicht gleich sind, werden Lissajous-Figuren um einiges komplexer. Betrachten Sie die folgenden Beispiele und sie erhalten vertikale/horizontale Frequenzverhältnisse:

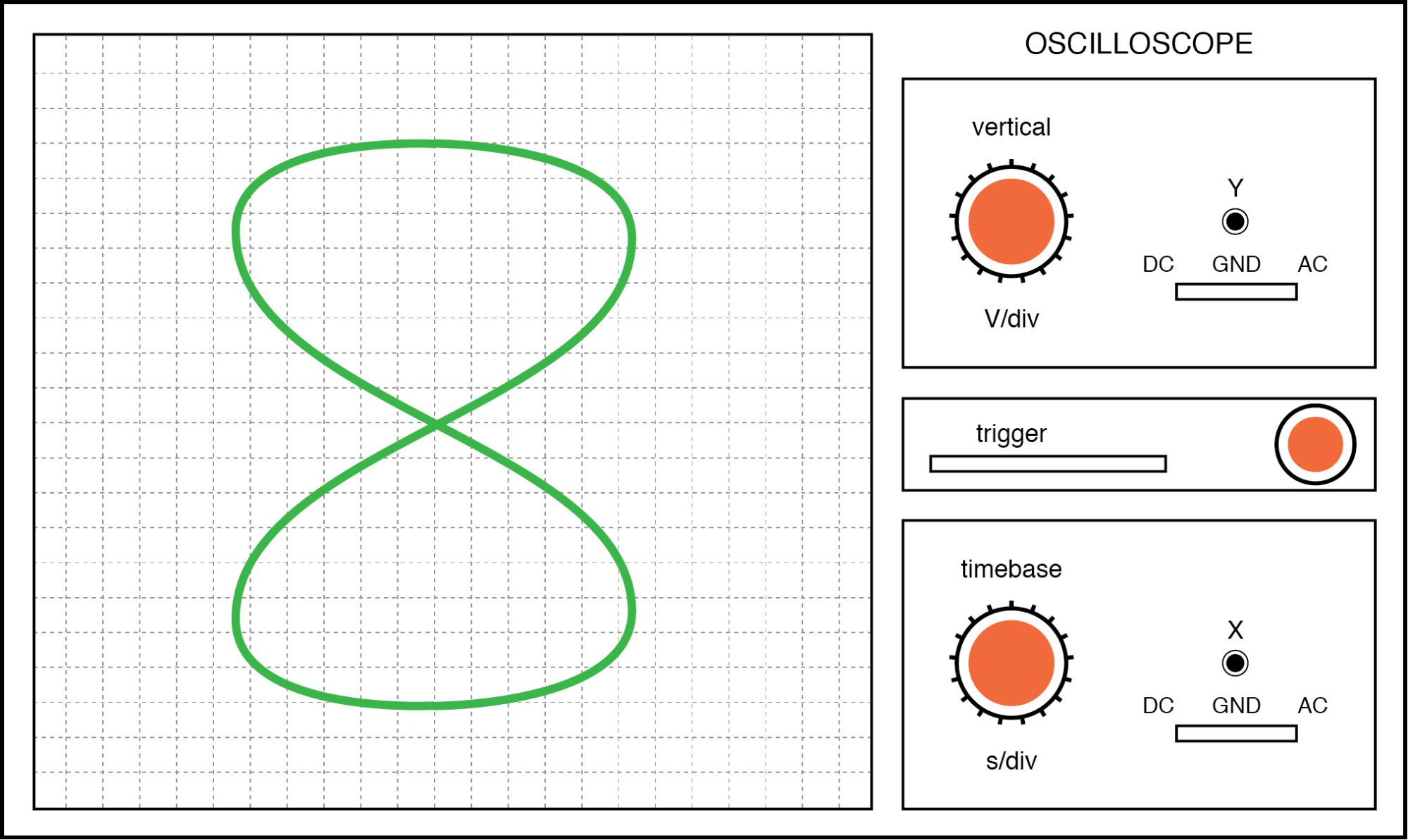
Lissajous-Figur:Die horizontale Frequenz ist doppelt so hoch wie die vertikale.

Je komplexer das Verhältnis zwischen horizontalen und vertikalen Frequenzen ist, desto komplexer ist die Lissajous-Figur. Betrachten Sie die folgende Abbildung eines 3:1-Frequenzverhältnisses zwischen horizontal und vertikal:

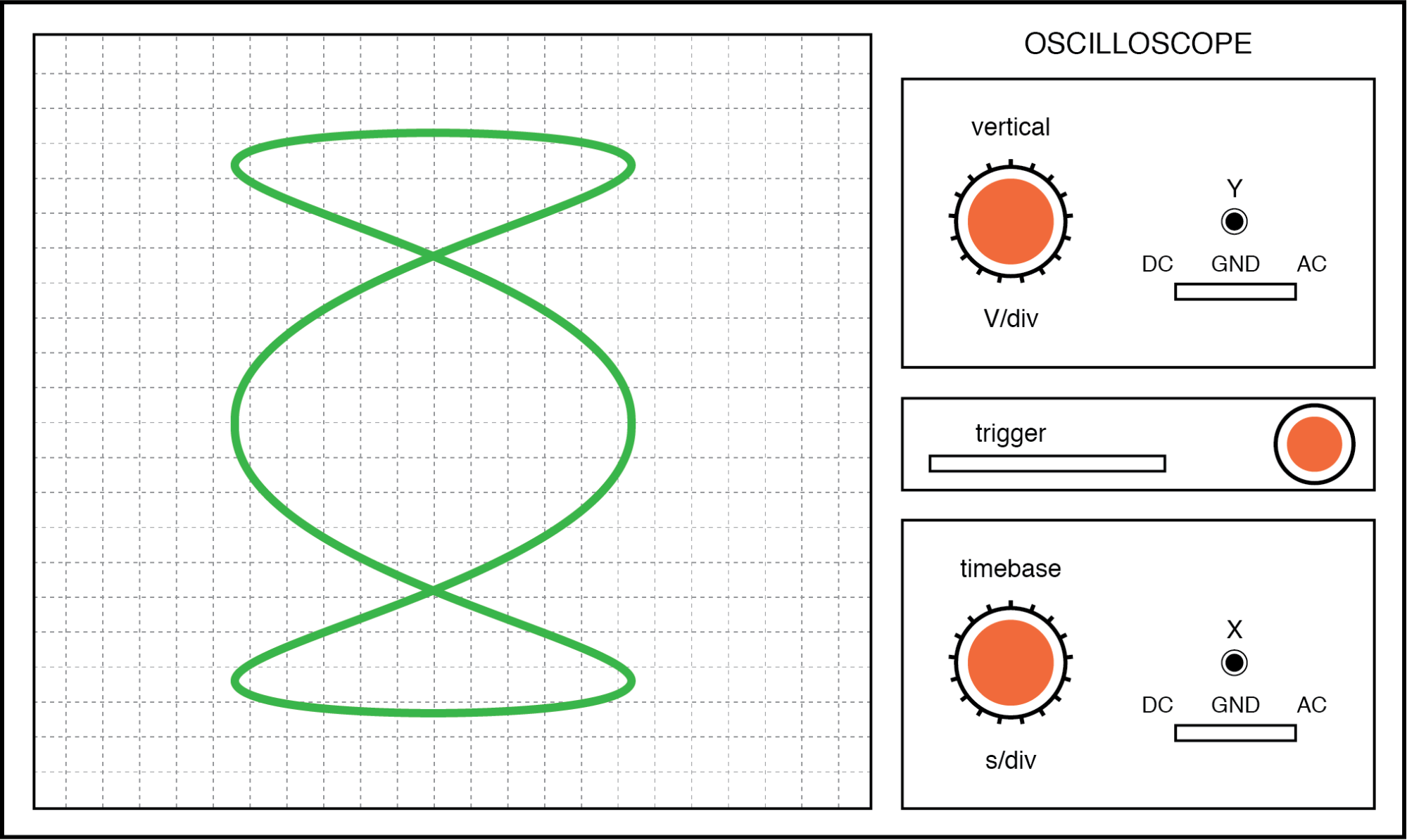
Lissajous-Figur:Die horizontale Frequenz ist dreimal so hoch wie die vertikale.

. . . und ein Frequenzverhältnis von 3:2 (horizontal =3, vertikal =2) in der Abbildung unten.

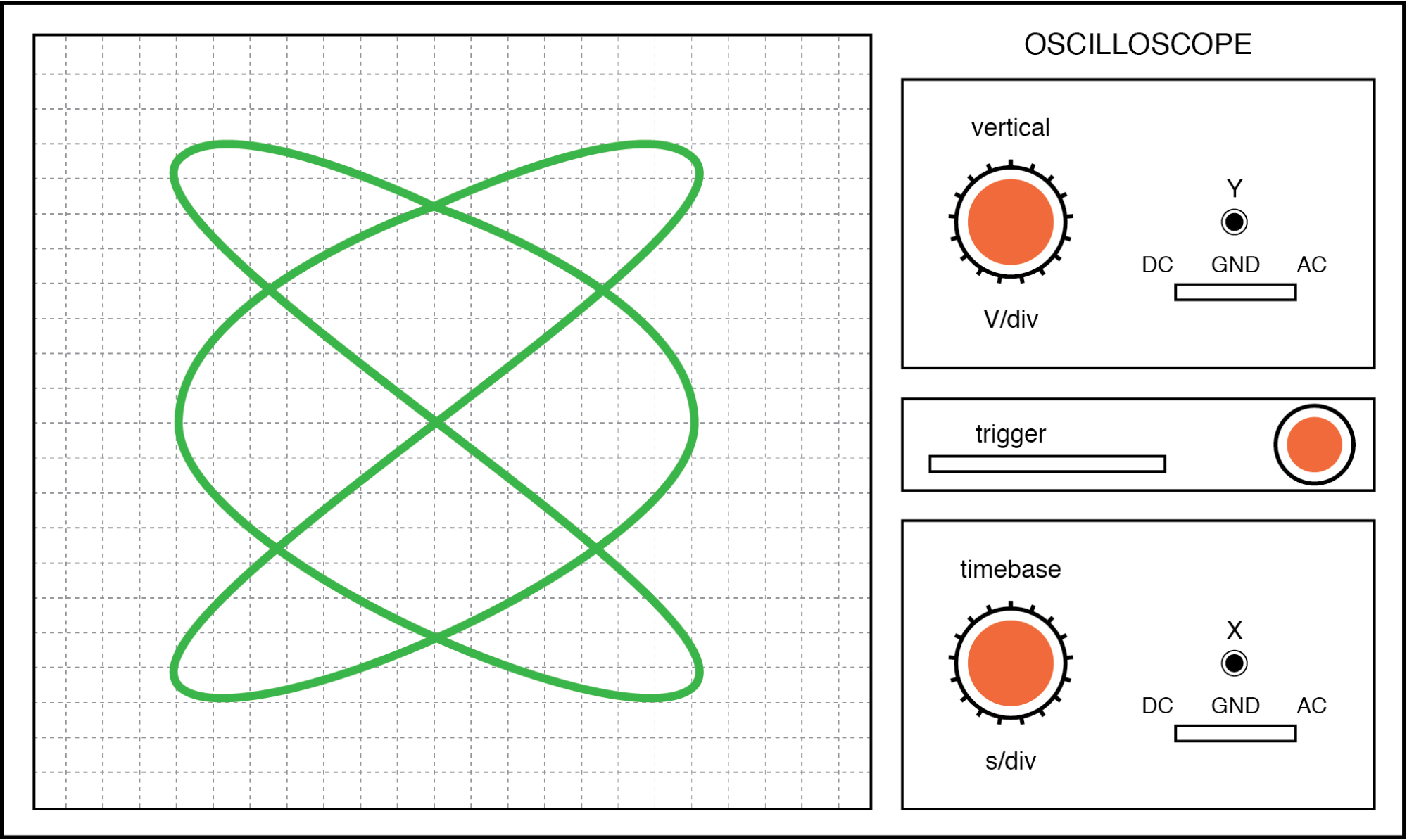
Lissajous-Figur:Das horizontale/vertikale Frequenzverhältnis beträgt 3:2.

In Fällen, in denen die Frequenzen der beiden AC-Signale nicht genau ein einfaches Verhältnis zueinander haben (aber nahe dran sind), scheint sich die Lissajous-Figur zu „bewegen“ und ändert langsam die Ausrichtung, während der Phasenwinkel zwischen den beiden Wellenformen zwischen 0° und rollt 180°.

Wenn die beiden Frequenzen in einem exakten ganzzahligen Verhältnis zueinander stehen, bleibt die Lissajous-Figur auf dem Bildschirm der CRT stabil.

Die Physik von Lissajous-Figuren beschränkt ihre Nützlichkeit als Frequenzvergleichstechnik auf Fälle, in denen die Frequenzverhältnisse einfache ganzzahlige Werte sind (1:1, 1:2, 1:3, 2:3, 3:4 usw.).

Trotz dieser Einschränkung sind Lissajous-Zahlen ein beliebtes Mittel zum Frequenzvergleich, wo immer ein zugängliches Frequenznormal (Signalgenerator) existiert.

RÜCKBLICK:

• Einige Frequenzmesser arbeiten nach dem Prinzip der mechanischen Resonanz und zeigen die Frequenz durch relative Oszillation zwischen einem Satz einzigartig abgestimmter „Blätter“ an, die bei der gemessenen Frequenz geschüttelt werden.
• Andere Frequenzmesser verwenden elektrische Resonanzkreise (normalerweise LC-Schwingkreise), um die Frequenz anzuzeigen. Eine oder beide Komponenten sind einstellbar, mit einem genau kalibrierten Einstellknopf, und ein empfindliches Messgerät misst die maximale Spannung oder den maximalen Strom am Resonanzpunkt.
• Die Häufigkeit kann auf vergleichende Weise gemessen werden, wie es bei der Verwendung einer CRT zur Erzeugung von Lissajous-Figuren der Fall ist. Referenzfrequenzsignale können mit hoher Genauigkeit durch Oszillatorschaltungen erzeugt werden, die Quarzkristalle als Resonanzvorrichtungen verwenden. Für höchste Präzision können Atomuhrsignalstandards (basierend auf den Resonanzfrequenzen einzelner Atome) verwendet werden.