Cramers Regelrechner – 2- und 3-Gleichungssystem

Cramers Regel und Rechner für die lineare Schaltungsanalyse | Schritt für Schritt mit gelösten Beispielen

Heute stellen wir Ihnen eine weitere einfache, aber leistungsstarke Schaltungsanalysetechnik vor, die als „Cramer-Regel bekannt ist „.

• SUPERMESH-Schaltungsanalyse | Schritt für Schritt mit gelöstem Beispiel

Aktualisierung: Wir haben den Online-Rechner für Cramer-Regeln hinzugefügt, mit dem Sie sowohl das System mit zwei Gleichungen als auch das System mit drei Gleichungen lösen können. Überprüfen Sie beide Cramer-Regelrechner in beiden Abschnitten des Beitrags. Danke

Nachfolgend finden Sie das Schritt-für-Schritt-Tutorial mit gelösten Beispielen, das erläutert, wie Sie einen komplexen elektrischen Schaltkreis und ein komplexes Netzwerk nach der Cramer-Regel lösen können.

Cramers Rule Calculator for 2×2 (Two Equations System)

Beispiel 2: Verwenden Sie Mesh Analysis, um die drei Mesh-Ströme in der Schaltung unten zu bestimmen. Verwenden Sie zur Vereinfachung die Cramersche Regel.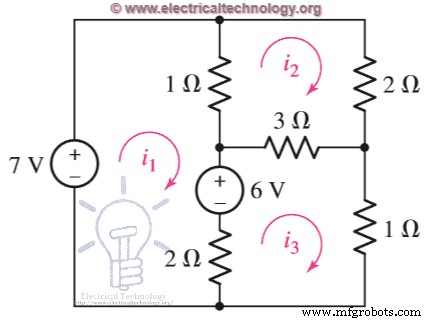 Wenden Sie zuerst die KVL nacheinander auf jedes Mesh an und schreiben Sie seine Gleichungen. -7+1(ich ₁ –ich ₂ ) +6+2(ich ₁ –ich ₃ ) =0         1(ich ₂ –ich ₁ ) + 2i ₂ + 3(ich ₂ –ich ₃ ) =0      2(ich ₃ –ich ₁ ) – 6+3(i ₃ –ich ₂ ) + 1ich ₃ =0 Vereinfachen,     3i ₁ –ich ₂ – 2ich ₃ =1                    … Gleichung….. (1)  –i ₁ + 6ich ₂ – 3ich ₃ =0                    … Gleichung….. (2) -2i ₁ – 3ich ₂ + 6ich ₃ =6                    … Eq….. (3) Schreiben Sie nun die obigen Gleichungen in Matrixform. 3ich ₁ – ich ₂ – 2ich ₃ =1   –i ₁ + 6ich ₂ – 3ich ₃ =0-2i ₁ – 3ich ₂ + 6ich ₃ =6  Nun finden wir die Koeffizientendeterminante von ∆. Wie werden wir das tun? Sehen Sie sich zur besseren Erklärung einfach die folgende Abbildung an. Klicken Sie auf das Bild, um es zu vergrößern  Der vollständige Schritt wird also unten gezeigt. ∆ =+3 (6 x 6) – (- 3 x –3) – (-1 (- 1 x 6)-(-2 x –3) + (-2 (-1 x –3) – (-2 x 6)∆ =81 -12 -30 =39 Finden Sie nun das ∆₁ auf die gleiche Weise wie oben erklärt. Aber ersetzen Sie einfach die erste Spalte der Matrix durch die „Antwortspalte“. Einzelheiten finden Sie in der unten gezeigten Abbildung. 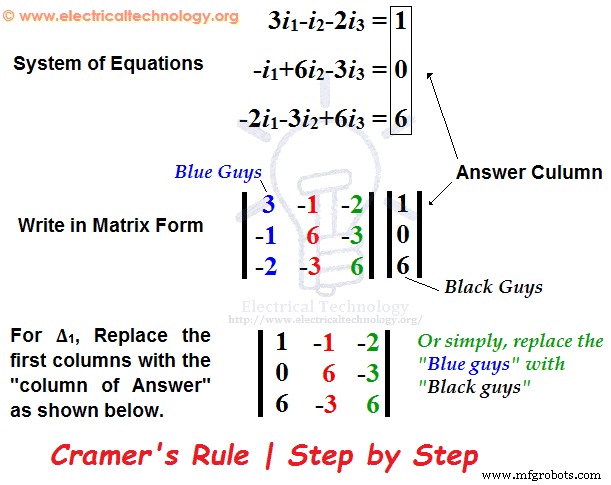Also, hier ist der vollständige Schritt, um ∆₁ zu finden . Hier haben wir die „Blue Guys“ in der ersten Spalte durch „Black Guys“ ersetzt :). 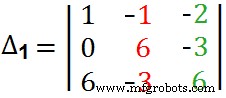=+1(36-9) – (–1[0+18]) –2(0- 36)=27 + 18 + 72∆₁ =117 Suchen Sie erneut das ∆₂ mit der gleichen Methode wie zuvor beschrieben. Ersetzen Sie einfach die zweite Spalte der Matrix durch die „Antwortspalte“, d. h. ersetzen Sie die „Roten“ in der mittleren Spalte durch „Schwarze“, wie unten gezeigt. 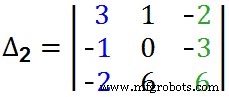=+3 (0 +18) -1[(-6)-(+6)] –2 (-6-0)=54+12+12 =78∆₂ =78 Finde schließlich das letzte ∆₃ . Ersetzen Sie einfach die dritte Spalte durch die „Antwortspalte“, d. h. ersetzen Sie die „Grünen Jungs“ in der dritten Spalte durch „Schwarze Jungs“, wie unten gezeigt. =+3 (6 x 6) – (-3 x 0) – [-1(-1 x 6) – (-2 x 0)] + [1(-1) x (-3) – (-2) x (6)]=108 + 6 + 15∆₃ =117 Jetzt lösen und finden Sie die unbekannten Werte des Stroms, d. h. i ₁ , ich ₂ und ich ₃ .Wie die Cramersche Regel besagt, sind Variablen, d.h. i ₁ =∆1/∆₁ , ich ₂ =∆/∆₂ und ich ₃ =∆/∆₃ . Daher ich ₁ =∆1/∆₁ =117/39ich ₁ =3A Und ich ₂ ,ich ₂ ==∆/∆₂ =78/39i ₂ =2A Und schließlich ich ₃ ;ich ₃ =∆/∆₃ =117/39ich ₃ =3A. Ich hoffe, dass Sie die Cramer-Regel sehr gut verstanden haben und Ihnen das Schritt-für-Schritt-Tutorial gefallen hat. Bitte vergessen Sie nicht, mit Ihren Freunden zu teilen. Geben Sie außerdem Ihre E-Mail-Adresse in das unten stehende Feld ein, um sich anzumelden. Wir werden Ihnen also weitere Tutorials wie das obige zusenden. Vielen Dank.

Zugehörige Beiträge und Schaltungsanalyse-Tools:

• Der Satz von Norton. Einfaches Schritt-für-Schritt-Verfahren mit Beispiel (Bildansichten)
• Der Satz von Thevenin. Einfaches Schritt-für-Schritt-Verfahren mit Beispiel (Bildansichten)
• Rechner für Elektro- und Elektroniktechnik online
• 10+ Design- und Simulationstools für Elektro-/Elektronikingenieure online
• Leiterplattendesign:So entwerfen Sie eine Leiterplatte (Schritt für Schritt und Bildansichten)
• 15 unverzichtbare Android-Apps für Elektro- und Elektronikingenieure und Studenten
• SUPERNODE Schaltungsanalyse | Schritt für Schritt mit gelöstem Beispiel
• SUPERMESH-Schaltungsanalyse | Schritt für Schritt mit gelöstem Beispiel
• Rechner für Elektro- und Elektronikingenieure