MATLAB-Integration
Integration befasst sich mit zwei grundsätzlich unterschiedlichen Arten von Problemen.
-
Beim ersten Typ ist die Ableitung einer Funktion gegeben und wir wollen die Funktion finden. Daher kehren wir den Prozess der Differenzierung im Grunde um. Dieser umgekehrte Prozess ist als Anti-Differenzierung oder Finden der primitiven Funktion oder Finden eines unbestimmten Integrals bekannt .
-
Die zweite Art von Problemen besteht darin, eine sehr große Anzahl sehr kleiner Mengen zu addieren und dann eine Grenze zu nehmen, wenn sich die Größe der Mengen Null nähert, während die Anzahl der Terme gegen unendlich tendiert. Dieser Prozess führt zur Definition des bestimmten Integrals .
Bestimmte Integrale werden zum Ermitteln von Fläche, Volumen, Schwerpunkt, Trägheitsmoment, von einer Kraft verrichteter Arbeit und in zahlreichen anderen Anwendungen verwendet.
Unbestimmtes Integral mit MATLAB finden
Wenn die Ableitung einer Funktion f(x) f'(x) ist, dann sagen wir per Definition, dass ein unbestimmtes Integral von f'(x) in Bezug auf x f(x) ist. Zum Beispiel, da die Ableitung (nach x) von x 2 2x ist, können wir sagen, dass ein unbestimmtes Integral von 2x gleich x 2 ist .
In Symbolen −
f'(x 2 ) =2x , also
∫ 2xdx =x 2 .
Unbestimmtes Integral ist nicht eindeutig, weil Ableitung von x 2 + c ist für jeden Wert einer Konstanten c ebenfalls 2x.
Dies wird symbolisch als −
ausgedrückt∫ 2xdx =x 2 +c .
Wobei c eine 'willkürliche Konstante' genannt wird.
MATLAB stellt ein int bereit Befehl zur Berechnung des Integrals eines Ausdrucks. Um einen Ausdruck für das unbestimmte Integral einer Funktion abzuleiten, schreiben wir −
int(f);
Zum Beispiel aus unserem vorherigen Beispiel −
syms x int(2*x)
MATLAB führt die obige Anweisung aus und gibt das folgende Ergebnis zurück −
ans = x^2
Beispiel 1
Lassen Sie uns in diesem Beispiel das Integral einiger häufig verwendeter Ausdrücke finden. Erstellen Sie eine Skriptdatei und geben Sie den folgenden Code ein −
syms x n int(sym(x^n)) f = 'sin(n*t)' int(sym(f)) syms a t int(a*cos(pi*t)) int(a^x)
Wenn Sie die Datei ausführen, zeigt sie das folgende Ergebnis an −
ans = piecewise([n == -1, log(x)], [n ~= -1, x^(n + 1)/(n + 1)]) f = sin(n*t) ans = -cos(n*t)/n ans = (a*sin(pi*t))/pi ans = a^x/log(a)
Beispiel 2
Erstellen Sie eine Skriptdatei und geben Sie den folgenden Code ein −
syms x n int(cos(x)) int(exp(x)) int(log(x)) int(x^-1) int(x^5*cos(5*x)) pretty(int(x^5*cos(5*x))) int(x^-5) int(sec(x)^2) pretty(int(1 - 10*x + 9 * x^2)) int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2) pretty(int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2))
Beachten Sie, dass hübsch Funktion gibt einen Ausdruck in einem besser lesbaren Format zurück.
Wenn Sie die Datei ausführen, zeigt sie das folgende Ergebnis an −
ans =
sin(x)
ans =
exp(x)
ans =
x*(log(x) - 1)
ans =
log(x)
ans =
(24*cos(5*x))/3125 + (24*x*sin(5*x))/625 - (12*x^2*cos(5*x))/125 + (x^4*cos(5*x))/5 - (4*x^3*sin(5*x))/25 + (x^5*sin(5*x))/5
2 4
24 cos(5 x) 24 x sin(5 x) 12 x cos(5 x) x cos(5 x)
----------- + ------------- - -------------- + ------------
3125 625 125 5
3 5
4 x sin(5 x) x sin(5 x)
------------- + -----------
25 5
ans =
-1/(4*x^4)
ans =
tan(x)
2
x (3 x - 5 x + 1)
ans =
- (7*x^6)/12 - (3*x^5)/5 + (5*x^4)/8 + x^3/2
6 5 4 3
7 x 3 x 5 x x
- ---- - ---- + ---- + --
12 5 8 2
Ermittlung eines bestimmten Integrals mit MATLAB
Per Definition ist ein bestimmtes Integral im Grunde der Grenzwert einer Summe. Wir verwenden bestimmte Integrale, um Flächen wie die Fläche zwischen einer Kurve und der x-Achse und die Fläche zwischen zwei Kurven zu finden. Bestimmte Integrale können auch in anderen Situationen verwendet werden, in denen die erforderliche Menge als Grenzwert einer Summe ausgedrückt werden kann.
Der int Funktion kann für die definitive Integration verwendet werden, indem Sie die Grenzen übergeben, über die Sie das Integral berechnen möchten.
Zu berechnen
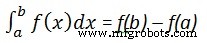
wir schreiben,
int(x, a, b)
Zum Beispiel, um den Wert von zu berechnen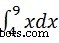 
wir schreiben −
int(x, 4, 9)
MATLAB führt die obige Anweisung aus und gibt das folgende Ergebnis zurück −
ans = 65/2
Das Folgende ist das Oktaväquivalent der obigen Berechnung −
pkg load symbolic
symbols
x = sym("x");
f = x;
c = [1, 0];
integral = polyint(c);
a = polyval(integral, 9) - polyval(integral, 4);
display('Area: '), disp(double(a));
Octave führt den Code aus und gibt das folgende Ergebnis zurück −
Area: 32.500
Eine alternative Lösung kann mit der von Octave bereitgestellten quad()-Funktion wie folgt gegeben werden −
pkg load symbolic
symbols
f = inline("x");
[a, ierror, nfneval] = quad(f, 4, 9);
display('Area: '), disp(double(a));
Octave führt den Code aus und gibt das folgende Ergebnis zurück −
Area: 32.500
Beispiel 1
Lassen Sie uns die Fläche berechnen, die zwischen der x-Achse und der Kurve y =x 3 eingeschlossen ist −2x+5 und die Ordinaten x =1 und x =2.
Die benötigte Fläche wird durch −
angegeben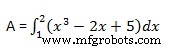
Erstellen Sie eine Skriptdatei und geben Sie den folgenden Code ein −
f = x^3 - 2*x +5;
a = int(f, 1, 2)
display('Area: '), disp(double(a));
Wenn Sie die Datei ausführen, zeigt sie das folgende Ergebnis an −
a = 23/4 Area: 5.7500
Das Folgende ist das Oktaväquivalent der obigen Berechnung −
pkg load symbolic
symbols
x = sym("x");
f = x^3 - 2*x +5;
c = [1, 0, -2, 5];
integral = polyint(c);
a = polyval(integral, 2) - polyval(integral, 1);
display('Area: '), disp(double(a));
Octave führt den Code aus und gibt das folgende Ergebnis zurück −
Area: 5.7500
Eine alternative Lösung kann mit der von Octave bereitgestellten quad()-Funktion wie folgt gegeben werden −
pkg load symbolic
symbols
x = sym("x");
f = inline("x^3 - 2*x +5");
[a, ierror, nfneval] = quad(f, 1, 2);
display('Area: '), disp(double(a));
Octave führt den Code aus und gibt das folgende Ergebnis zurück −
Area: 5.7500
Beispiel 2
Finde die Fläche unter der Kurve:f(x) =x 2 cos(x) für −4 ≤ x ≤ 9.
Erstellen Sie eine Skriptdatei und schreiben Sie den folgenden Code −
f = x^2*cos(x);
ezplot(f, [-4,9])
a = int(f, -4, 9)
disp('Area: '), disp(double(a));
Wenn Sie die Datei ausführen, zeichnet MATLAB den Graphen −
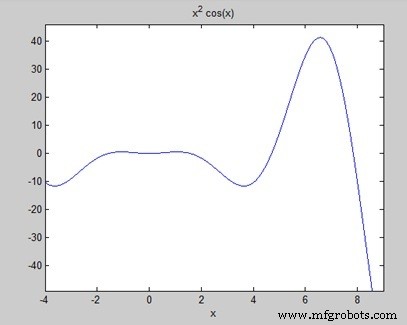
Die Ausgabe ist unten angegeben −
a = 8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9) Area: 0.3326
Das Folgende ist das Oktaväquivalent der obigen Berechnung −
pkg load symbolic
symbols
x = sym("x");
f = inline("x^2*cos(x)");
ezplot(f, [-4,9])
print -deps graph.eps
[a, ierror, nfneval] = quad(f, -4, 9);
display('Area: '), disp(double(a));
MATLAB