MATLAB - Transformationen

MATLAB bietet Befehle zum Arbeiten mit Transformationen, wie z. B. Laplace- und Fourier-Transformationen. Transformationen werden in Wissenschaft und Technik als Werkzeug zur Vereinfachung der Analyse und zur Betrachtung von Daten aus einem anderen Blickwinkel verwendet.

Beispielsweise ermöglicht uns die Fourier-Transformation, ein Signal, das als Funktion der Zeit dargestellt wird, in eine Funktion der Frequenz umzuwandeln. Die Laplace-Transformation ermöglicht es uns, eine Differentialgleichung in eine algebraische Gleichung umzuwandeln.

MATLAB stellt den Laplace bereit , Fourier und fft Befehle zum Arbeiten mit Laplace-, Fourier- und Fast-Fourier-Transformationen.

Die Laplace-Transformation

Die Laplace-Transformation einer Funktion der Zeit f(t) ist durch das folgende Integral −

gegeben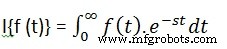

Die Laplace-Transformation wird auch als Transformation von f(t) nach F(s) bezeichnet. Sie können sehen, dass dieser Transformations- oder Integrationsprozess f(t), eine Funktion der symbolischen Variablen t, in eine andere Funktion F(s) mit einer anderen Variablen s umwandelt.

Die Laplace-Transformation verwandelt Differentialgleichungen in algebraische. Um eine Laplace-Transformation einer Funktion f(t) zu berechnen, schreiben Sie −

laplace(f(t))

Beispiel

In diesem Beispiel berechnen wir die Laplace-Transformation einiger häufig verwendeter Funktionen.

Erstellen Sie eine Skriptdatei und geben Sie den folgenden Code ein −

syms s t a b w

laplace(a)
laplace(t^2)
laplace(t^9)
laplace(exp(-b*t))
laplace(sin(w*t))
laplace(cos(w*t))

Wenn Sie die Datei ausführen, zeigt sie das folgende Ergebnis an −

ans =
   1/s^2

ans =
   2/s^3

ans =
   362880/s^10

ans =
   1/(b + s)
  
ans =
   w/(s^2 + w^2)
  
ans =
   s/(s^2 + w^2)

Die inverse Laplace-Transformation

MATLAB ermöglicht es uns, die inverse Laplace-Transformation mit dem Befehl ilaplace zu berechnen .

Zum Beispiel

ilaplace(1/s^3)

MATLAB führt die obige Anweisung aus und zeigt das Ergebnis an −

ans =
   t^2/2

Beispiel

Erstellen Sie eine Skriptdatei und geben Sie den folgenden Code ein −

syms s t a b w

ilaplace(1/s^7)
ilaplace(2/(w+s))
ilaplace(s/(s^2+4))
ilaplace(exp(-b*t))
ilaplace(w/(s^2 + w^2))
ilaplace(s/(s^2 + w^2))

Wenn Sie die Datei ausführen, zeigt sie das folgende Ergebnis an −

ans =
   t^6/720

ans =
   2*exp(-t*w)

ans =
   cos(2*t)

ans =
   ilaplace(exp(-b*t), t, x)

ans =
   sin(t*w)

ans =
   cos(t*w)

Die Fourier-Transformationen

Fourier-Transformationen transformieren üblicherweise eine mathematische Funktion der Zeit, f(t), in eine neue Funktion, die manchmal mit oder F bezeichnet wird, deren Argument die Frequenz mit Einheiten von Zyklen/s (Hertz) oder Bogenmaß pro Sekunde ist. Die neue Funktion ist dann als Fourier-Transformation bzw. Frequenzspektrum der Funktion f bekannt.

Beispiel

Erstellen Sie eine Skriptdatei und geben Sie den folgenden Code ein −

syms x 
f = exp(-2*x^2);     %our function
ezplot(f,[-2,2])     % plot of our function
FT = fourier(f)      % Fourier transform

Wenn Sie die Datei ausführen, zeichnet MATLAB das folgende Diagramm −

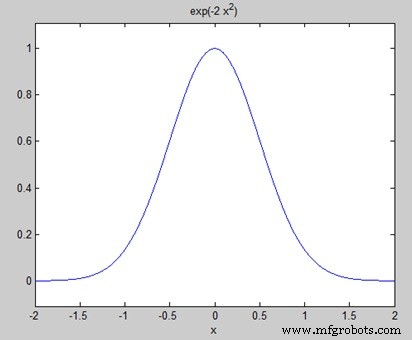
Das folgende Ergebnis wird angezeigt −

FT =
   (2^(1/2)*pi^(1/2)*exp(-w^2/8))/2

Darstellung der Fourier-Transformation als −

ezplot(FT)

Ergibt den folgenden Graphen −

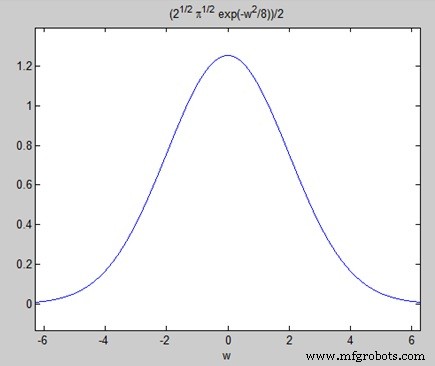
Inverse Fourier-Transformationen

MATLAB stellt den ifourier bereit Befehl zur Berechnung der inversen Fourier-Transformation einer Funktion. Zum Beispiel

f = ifourier(-2*exp(-abs(w)))

MATLAB führt die obige Anweisung aus und zeigt das Ergebnis an −

f =
   -2/(pi*(x^2 + 1))