Verstehen lokaler Minima in neuronalen Netzwerkschulungen

In diesem Artikel wird eine Komplikation beschrieben, die Ihr Perceptron daran hindern kann, eine angemessene Klassifizierungsgenauigkeit zu erreichen.

In der Serie über neuronale Netze von AAC haben wir eine breite Palette von Themen im Zusammenhang mit dem Verständnis und der Entwicklung von mehrschichtigen neuronalen Perceptron-Netzen behandelt. Informieren Sie sich vor dem Lesen dieses Artikels über lokale Minima über den Rest der folgenden Serie:

1. Wie man eine Klassifikation mit einem neuronalen Netzwerk durchführt:Was ist das Perzeptron?
2. So verwenden Sie ein einfaches Beispiel für ein neuronales Perceptron-Netzwerk zum Klassifizieren von Daten
3. Wie man ein grundlegendes neuronales Perceptron-Netzwerk trainiert
4. Einfaches neuronales Netzwerk-Training verstehen
5. Eine Einführung in die Trainingstheorie für neuronale Netze
6. Lernrate in neuronalen Netzen verstehen
7. Fortgeschrittenes maschinelles Lernen mit dem mehrschichtigen Perzeptron
8. Die Sigmoid-Aktivierungsfunktion:Aktivierung in mehrschichtigen neuronalen Perzeptronnetzwerken
9. Wie man ein mehrschichtiges neuronales Perceptron-Netzwerk trainiert
10. Verstehen von Trainingsformeln und Backpropagation für mehrschichtige Perzeptronen
11. Neurale Netzwerkarchitektur für eine Python-Implementierung
12. So erstellen Sie ein mehrschichtiges neuronales Perceptron-Netzwerk in Python
13. Signalverarbeitung mit neuronalen Netzen:Validierung im neuronalen Netzdesign
14. Trainings-Datasets für neuronale Netze:So trainieren und validieren Sie ein neuronales Python-Netz
15. Wie viele versteckte Schichten und versteckte Knoten benötigt ein neuronales Netzwerk?
16. So erhöhen Sie die Genauigkeit eines neuronalen Hidden-Layer-Netzwerks
17. Integration von Bias-Knoten in Ihr neuronales Netzwerk
18. Lokale Minima beim Training neuronaler Netzwerke verstehen

Das Training neuronaler Netzwerke ist ein komplexer Prozess. Glücklicherweise müssen wir es nicht perfekt verstehen, um davon zu profitieren:Die von uns verwendeten Netzwerkarchitekturen und Trainingsverfahren führen tatsächlich zu funktionalen Systemen, die eine sehr hohe Klassifikationsgenauigkeit erreichen. Es gibt jedoch einen theoretischen Aspekt der Ausbildung, der, obwohl er etwas abstrus ist, unsere Aufmerksamkeit verdient.

Wir nennen es „das Problem der lokalen Minima“.

Warum verdienen lokale Minima unsere Aufmerksamkeit?

Naja, ich bin mir nicht sicher. Als ich zum ersten Mal von neuronalen Netzen hörte, hatte ich den Eindruck, dass lokale Minima tatsächlich ein erhebliches Hindernis für ein erfolgreiches Training sind, zumindest wenn es sich um komplexe Input-Output-Beziehungen handelt. Ich glaube jedoch, dass die neuere Forschung die Bedeutung lokaler Minima herunterspielt. Vielleicht haben neuere Netzwerkstrukturen und Verarbeitungstechniken die Schwere des Problems gemildert, oder vielleicht haben wir einfach ein besseres Verständnis dafür, wie neuronale Netzwerke tatsächlich zur gewünschten Lösung navigieren.

Am Ende dieses Artikels werden wir uns den aktuellen Status der lokalen Minima noch einmal ansehen. Vorerst beantworte ich meine Frage wie folgt:Lokale Minima verdienen unsere Aufmerksamkeit, weil sie uns erstens helfen, tiefer darüber nachzudenken, was wirklich passiert, wenn wir ein Netzwerk über Gradientenabstieg trainieren, und zweitens, weil lokale Minima – oder zumindest waren —wird als erhebliches Hindernis für die erfolgreiche Implementierung neuronaler Netze in realen Systemen angesehen.

Was ist ein lokales Minimum?

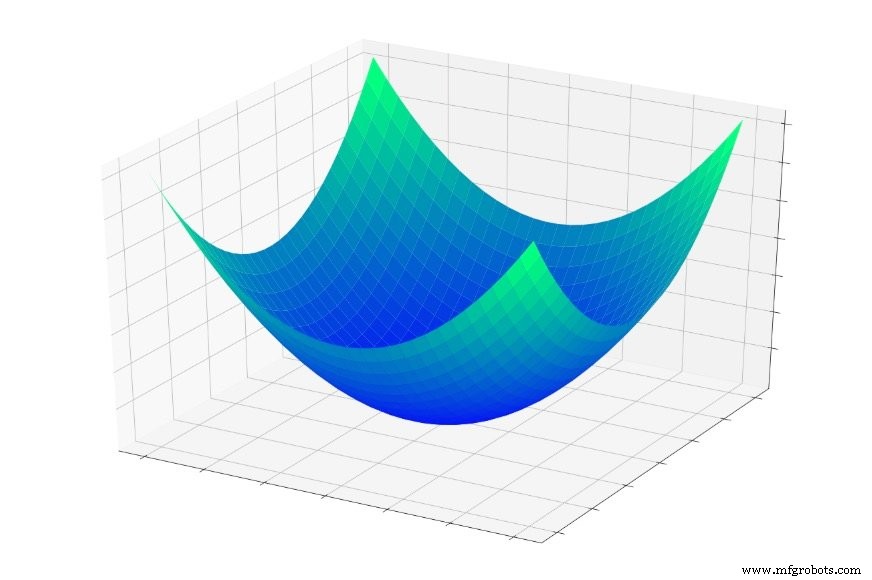
In Teil 5 betrachteten wir die unten gezeigte „Fehlerschüssel“ und ich beschrieb das Training im Wesentlichen als Suche nach dem tiefsten Punkt in dieser Schüssel.

(Hinweis :In diesem Artikel basieren meine Bilder und Erklärungen auf unserem intuitiven Verständnis dreidimensionaler Strukturen, aber denken Sie daran, dass die allgemeinen Konzepte nicht auf dreidimensionale Beziehungen beschränkt sind. Tatsächlich verwenden wir häufig neuronale Netze, deren Dimensionalität zwei Eingabevariablen und eine Ausgabevariable weit überschreitet.)

Wenn Sie in diese Schüssel springen würden, würden Sie jedes Mal nach unten rutschen. Egal wo du anfängst , landen Sie am tiefsten Punkt der gesamten Fehlerfunktion. Dieser tiefste Punkt ist das globale Minimum . Wenn ein Netzwerk auf das globale Minimum konvergiert hat, hat es seine Fähigkeit zur Klassifizierung der Trainingsdaten optimiert und theoretisch , das ist das grundlegende Ziel des Trainings:die Gewichte weiter zu modifizieren, bis das globale Minimum erreicht ist.

Wir wissen jedoch, dass neuronale Netze in der Lage sind, äußerst komplexe Input-Output-Beziehungen anzunähern. Die obige Fehlerschüssel passt nicht gerade in die Kategorie „extrem komplex“. Es ist einfach ein Diagramm der Funktion \(f(x,y) =x^2 + y^2\).

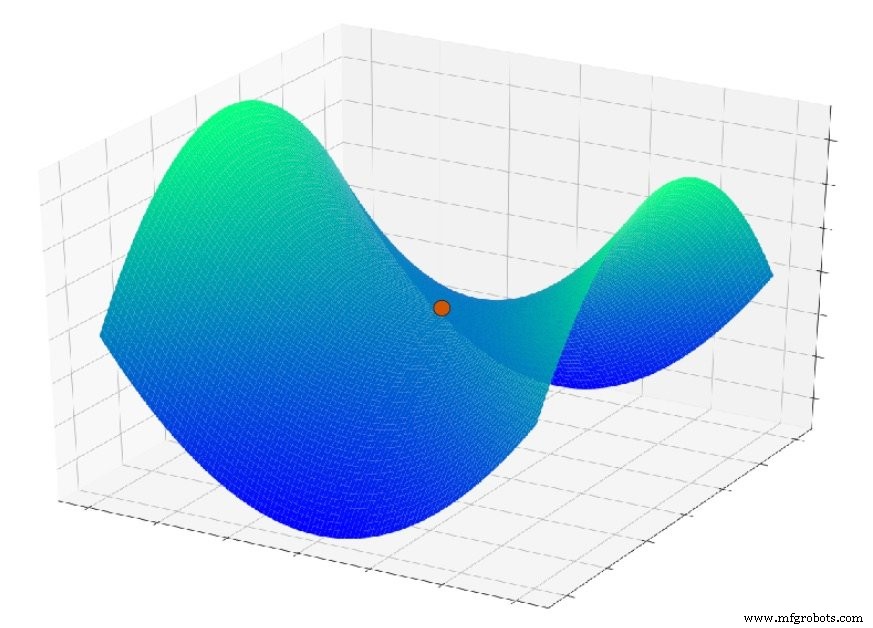
Aber jetzt stellen Sie sich vor, die Fehlerfunktion sieht ungefähr so ​​aus:

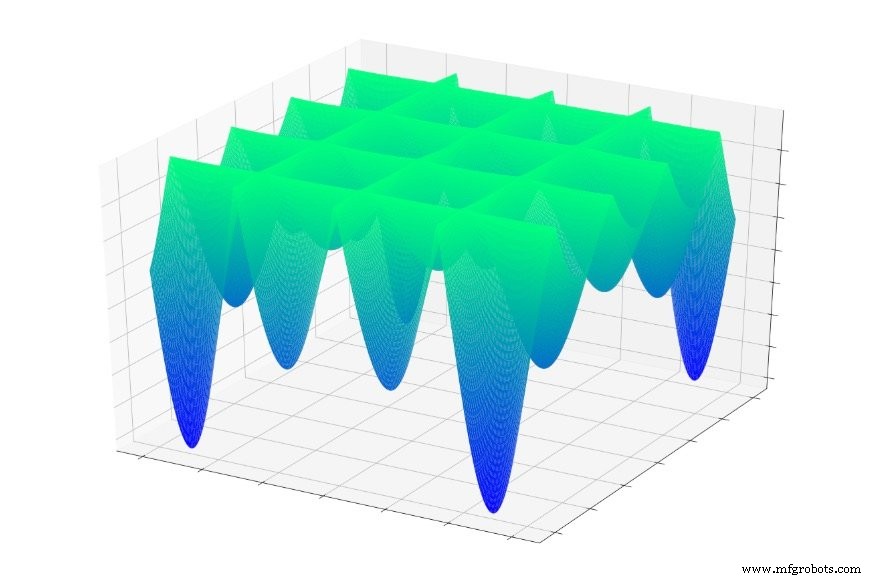
Oder dies:

Oder dies:

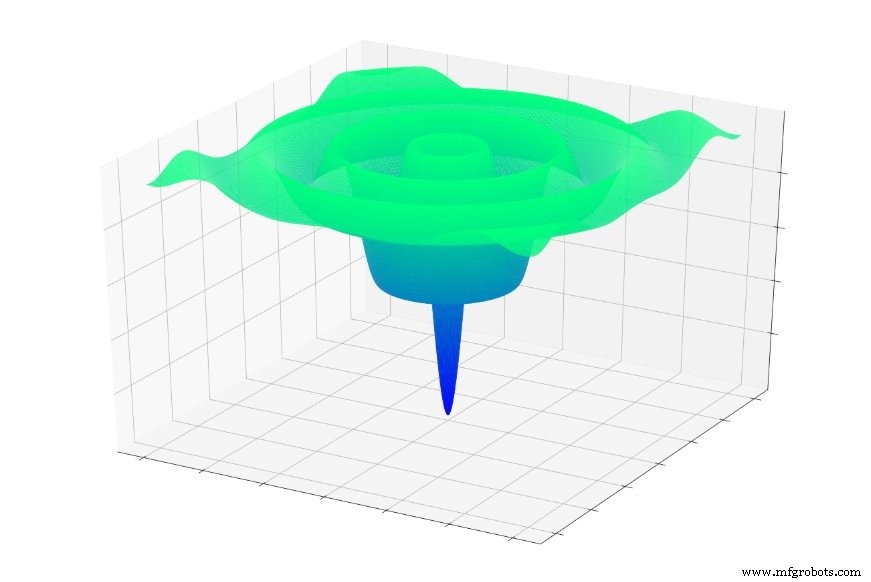
Wenn Sie zufällig in eine dieser Funktionen gesprungen sind, rutschen Sie oft in ein lokales Minimum ab. Sie befinden sich am tiefsten Punkt eines lokalisierten Abschnitts des Diagramms, befinden sich jedoch möglicherweise nicht in der Nähe des globalen mindestens.

Das gleiche kann einem neuronalen Netz passieren. Der Gradientenabstieg basiert auf lokalem Informationen, von denen wir hoffen, dass sie ein Netzwerk in Richtung global führen werden Minimum. Das Netzwerk hat keine Vorkenntnisse über die Eigenschaften der gesamten Fehleroberfläche, und wenn es einen Punkt erreicht, der wie der Boden der Fehleroberfläche aussieht, basierend auf lokalen Informationen , es kann keine topografische Karte herausziehen und feststellen, dass es bergauf zurückfahren muss um den Punkt zu finden, der tatsächlich niedriger ist als alle anderen.

Wenn wir einen grundlegenden Gradientenabstieg implementieren, sagen wir dem Netzwerk:„Finde den Grund einer Fehleroberfläche und bleib dort.“ Wir sagen nicht:„Finden Sie den Grund einer Fehleroberfläche, notieren Sie Ihre Koordinaten und wandern Sie dann weiter bergauf und abwärts, bis Sie die nächste finden. Lass es mich wissen, wenn du fertig bist.“

Wollen wir wirklich das globale Minimum finden?

Es ist vernünftig anzunehmen, dass das globale Minimum die optimale Lösung darstellt, und zu dem Schluss zu kommen, dass lokale Minima problematisch sind, da das Training in einem lokalen Minimum „blockieren“ könnte, anstatt sich dem globalen Minimum zu nähern.

Ich denke, dass diese Annahme in vielen Fällen gültig ist, aber relativ neue Forschungen zu Verlustoberflächen neuronaler Netzwerke legen nahe, dass hochkomplexe Netzwerke tatsächlich von lokalen Minima profitieren können, da ein Netzwerk, das das globale Minimum findet, übertrainiert wird und daher weniger sein wird effektiv bei der Verarbeitung neuer Eingangs-Samples.

Ein weiteres Problem, das hier ins Spiel kommt, ist ein Oberflächenmerkmal, das als Sattelpunkt bezeichnet wird; Sie können ein Beispiel in der Grafik unten sehen. Es ist möglich, dass im Kontext echter neuronaler Netzwerkanwendungen Sattelpunkte in der Fehleroberfläche tatsächlich ein ernsteres Problem darstellen als lokale Minima.

Schlussfolgerung

Ich hoffe, dass Ihnen diese Diskussion über lokale Minima gefallen hat. Im nächsten Artikel werden wir einige Techniken besprechen, die einem neuronalen Netzwerk helfen, das globale Minimum zu erreichen (wenn es tatsächlich das ist, was wir wollen).