So bauen Sie einen Variations-Autoencoder mit TensorFlow

Lernen Sie die wichtigsten Teile eines Autoencoders, wie ein Variations-Autoencoder ihn verbessert und wie Sie einen Variations-Autoencoder mit TensorFlow erstellen und trainieren.

Im Laufe der Jahre haben wir gesehen, wie viele Bereiche und Branchen die Leistungsfähigkeit der künstlichen Intelligenz (KI) genutzt haben, um die Grenzen der Forschung zu verschieben. Datenkomprimierung und -rekonstruktion sind keine Ausnahme, wo die Anwendung künstlicher Intelligenz verwendet werden kann, um robustere Systeme aufzubauen.

In diesem Artikel werden wir uns einen sehr beliebten Anwendungsfall von KI ansehen, um Daten zu komprimieren und die komprimierten Daten mit einem Autoencoder zu rekonstruieren.

Autoencoder-Anwendungen

Autoencoder haben die Aufmerksamkeit vieler Leute im Bereich des maschinellen Lernens auf sich gezogen, eine Tatsache, die durch die Verbesserung von Autoencodern und die Erfindung mehrerer Varianten deutlich wurde. Sie haben einige vielversprechende (wenn nicht sogar state-of-the-art) Ergebnisse in verschiedenen Bereichen wie neuronaler maschineller Übersetzung, Wirkstoffforschung, Bildrauschunterdrückung und einigen anderen erbracht.

Teile des Autoencoders

Autoencoder lernen wie die meisten neuronalen Netze, indem sie Gradienten rückwärts ausbreiten, um einen Satz von Gewichtungen zu optimieren – aber der auffälligste Unterschied zwischen der Architektur von Autoencodern und der der meisten neuronalen Netze ist ein Engpass. Dieser Engpass ist ein Mittel, um unsere Daten in eine Darstellung niedrigerer Dimensionen zu komprimieren. Zwei weitere wichtige Teile eines Autoencoders sind der Encoder und der Decoder.

Die Verschmelzung dieser drei Komponenten bildet einen "Vanille"-Autoencoder, obwohl komplexere einige zusätzliche Komponenten haben können.

Schauen wir uns diese Komponenten unabhängig voneinander an.

Encoder

Dies ist die erste Stufe der Datenkomprimierung und -rekonstruktion und kümmert sich tatsächlich um die Datenkomprimierungsstufe. Der Codierer ist ein neuronales Feed-Forward-Netzwerk, das Datenmerkmale (wie Pixel im Fall der Bildkomprimierung) aufnimmt und einen latenten Vektor mit einer Größe ausgibt, die kleiner ist als die Größe der Datenmerkmale.

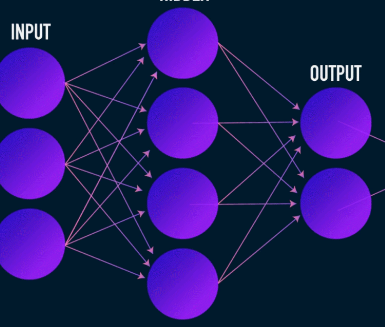
Bild mit freundlicher Genehmigung von James Loy

Um die Rekonstruktion der Daten robust zu machen, optimiert der Codierer seine Gewichtungen während des Trainings, um die wichtigsten Merkmale der Eingabedatendarstellung in den kleinen latenten Vektor zu pressen. Dadurch wird sichergestellt, dass der Decoder über genügend Informationen über die Eingabedaten verfügt, um die Daten mit minimalem Verlust zu rekonstruieren.

Latenter Vektor (Engpass)

Der Engpass oder die latente Vektorkomponente des Autoencoders ist der wichtigste Teil – und er wird noch wichtiger, wenn wir seine Größe auswählen müssen.

Die Ausgabe des Encoders liefert uns den latenten Vektor und soll die wichtigsten Merkmalsdarstellungen unserer Eingabedaten enthalten. Es dient auch als Eingabe für den Decoderteil und gibt die nützliche Darstellung zur Rekonstruktion an den Decoder weiter.

Wenn Sie eine kleinere Größe für den latenten Vektor wählen, erhalten wir eine Darstellung der Eingabedaten-Features mit weniger Informationen über die Eingabedaten. Die Wahl einer viel größeren latenten Vektorgröße spielt die ganze Idee der Komprimierung mit Autoencodern herunter und erhöht auch die Rechenkosten.

Decoder

Diese Phase schließt unseren Datenkompressions- und Rekonstruktionsprozess ab. Genau wie der Encoder ist auch diese Komponente ein neuronales Feed-Forward-Netzwerk, sieht jedoch strukturell etwas anders aus als der Encoder. Dieser Unterschied rührt von der Tatsache her, dass der Decoder als Eingabe einen latenten Vektor von geringerer Größe als die Ausgabe des Decoders verwendet.

Die Funktion des Decoders besteht darin, eine Ausgabe aus dem latenten Vektor zu erzeugen, die der Eingabe sehr nahe kommt.

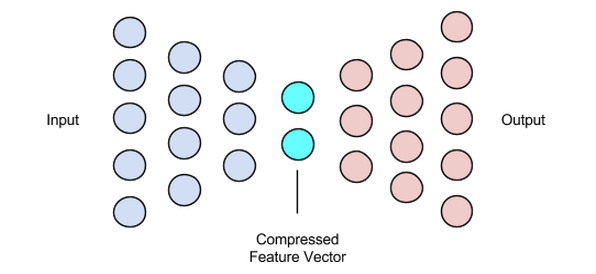
Bild mit freundlicher Genehmigung von Chiman Kwan

Training von Autoencodern

Normalerweise bauen wir beim Training von Autoencodern diese Komponenten zusammen, anstatt sie unabhängig voneinander zu bauen. Wir trainieren sie Ende-zu-Ende mit einem Optimierungsalgorithmus wie dem Gradientenabstieg oder dem ADAM-Optimierer.

Verlustfunktionen

Ein erwähnenswerter Teil des Autoencoder-Trainingsverfahrens ist die Verlustfunktion. Die Datenrekonstruktion ist eine Generierungsaufgabe und im Gegensatz zu anderen maschinellen Lernaufgaben, bei denen unser Ziel darin besteht, die Wahrscheinlichkeit der Vorhersage der richtigen Klasse zu maximieren, steuern wir unser Netzwerk so, dass eine Ausgabe nahe der Eingabe erfolgt.

Wir können dieses Ziel mit mehreren Verlustfunktionen wie l1, l2, mittlerer quadratischer Fehler und einigen anderen erreichen. Was diese Verlustfunktionen gemeinsam haben, ist, dass sie die Differenz (d. h. wie weit oder identisch) zwischen Eingabe und Ausgabe messen, wodurch jede von ihnen zu einer geeigneten Wahl wird.

Autoencoder-Netzwerke

Während dieser ganzen Zeit haben wir ein mehrschichtiges Perzeptron verwendet, um sowohl unseren Encoder als auch unseren Decoder zu entwerfen – aber es stellt sich heraus, dass wir spezialisiertere Frameworks wie Convolutional Neural Networks (CNNs) verwenden können, um mehr räumliche Informationen über unsere Eingabedaten zu erfassen im Fall der Bilddatenkompression.

Überraschenderweise hat die Forschung gezeigt, dass rekurrente Netzwerke, die als Autoencoder für Textdaten verwendet werden, sehr gut funktionieren, aber darauf werden wir im Rahmen dieses Artikels nicht eingehen. Das Konzept eines Codierer-latenten Vektor-Decodierers, das in dem mehrschichtigen Perzeptron verwendet wird, gilt immer noch für Faltungs-Autocodierer. Der einzige Unterschied besteht darin, dass wir Decoder und Encoder mit Faltungsschichten konzipieren.

Alle diese Autoencoder-Netzwerke würden für die Komprimierungsaufgabe ziemlich gut funktionieren, aber es gibt ein Problem.

Die von uns besprochenen Netzwerke haben null Kreativität. Was ich mit null Kreativität meine, ist, dass sie nur Ergebnisse generieren können, die sie gesehen oder mit denen sie trainiert wurden.

Wir können ein gewisses Maß an Kreativität fördern, indem wir unser Architekturdesign ein wenig optimieren. Das Ergebnis wird als Variations-Autoencoder bezeichnet.

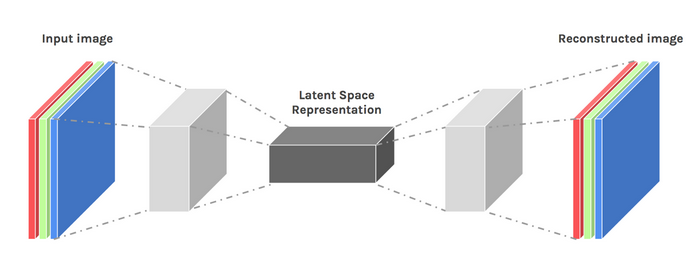
Bild mit freundlicher Genehmigung von Dawid Kopczyk

Variationaler Autoencoder

Der Variations-Autoencoder führt zwei wesentliche Designänderungen ein:

• Anstatt die Eingabe in eine latente Kodierung zu übersetzen, geben wir zwei Parametervektoren aus:Mittelwert und Varianz.
• Ein zusätzlicher Verlustterm, der KL-Divergenzverlust genannt wird, wird der anfänglichen Verlustfunktion hinzugefügt.

Die Idee hinter dem Variations-Autoencoder ist, dass unser Decoder unsere Daten rekonstruieren soll, indem er latente Vektoren verwendet, die aus Verteilungen abgetastet werden, die durch einen Mittelwertvektor und einen vom Encoder erzeugten Varianzvektor parametrisiert sind.

Das Abtasten von Merkmalen aus einer Verteilung gewährt dem Decoder einen kontrollierten Raum zum Generieren. Nach dem Training eines Variations-Autoencoders generiert der Encoder jedes Mal, wenn wir einen Vorwärtsdurchlauf mit Eingabedaten durchführen, einen Mittelwert- und Varianzvektor, der für die Bestimmung der Verteilung verantwortlich ist, von der der latente Vektor abgetastet werden soll.

Der Mittelwertvektor bestimmt, wo die Kodierung der Eingabedaten zentriert werden sollte, und die Varianz bestimmt den radialen Raum oder Kreis, aus dem wir die Kodierung auswählen möchten, um eine realistische Ausgabe zu erzeugen. Das bedeutet, dass unser Variations-Autoencoder bei jedem Vorwärtsdurchlauf mit denselben Eingabedaten verschiedene Varianten der Ausgabe generieren kann, die um den Mittelwertvektor und innerhalb des Varianzraums zentriert sind.

Zum Vergleich:Wenn wir einen Standard-Autoencoder betrachten und versuchen, eine Ausgabe zu generieren, auf die das Netzwerk nicht trainiert wurde, erzeugt er unrealistische Ausgaben aufgrund von Diskontinuitäten im latenten Vektorraum, den der Encoder erzeugt.

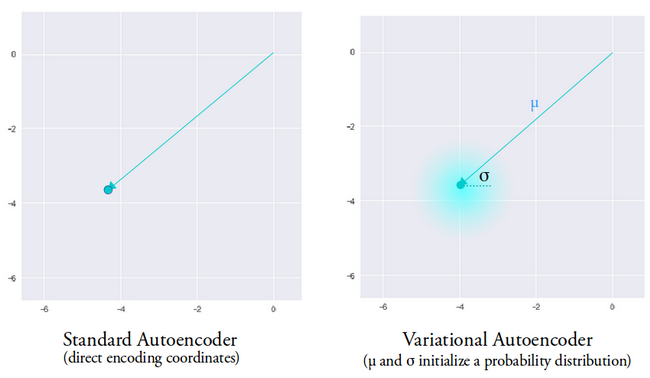
Bild mit freundlicher Genehmigung von Irhum Shafkat

Da wir nun ein intuitives Verständnis eines Variations-Autoencoders haben, sehen wir uns an, wie man einen in TensorFlow erstellt.

TensorFlow-Code für einen Variations-Autoencoder

Wir beginnen unser Beispiel damit, dass wir unseren Datensatz vorbereiten. Der Einfachheit halber verwenden wir den MNIST-Datensatz.

(train_images, _), (test_images, _) =tf.keras.datasets.mnist.load_data()

train_images =train_images.reshape(train_images.shape[0], 28, 28, 1).astype('float32')

test_images =test_images.reshape(test_images.shape[0], 28, 28, 1).astype('float32')

# Normalisieren der Bilder auf den Bereich von [0., 1.]

train_images /=255.

test_images /=255.

# Binarisierung

train_images[train_images>=.5] =1.

train_images[train_images <.5] =0.

test_images[test_images>=.5] =1.

test_images[test_images <.5] =0.

TRAIN_BUF =60000

BATCH_SIZE =100

TEST_BUF =10000

train_dataset =tf.data.Dataset.from_tensor_slices(train_images).shuffle(TRAIN_BUF).batch(BATCH_SIZE)

test_dataset =tf.data.Dataset.from_tensor_slices(test_images).shuffle(TEST_BUF).batch(BATCH_SIZE)

Datensatz abrufen und für die Aufgabe vorbereiten.

Klasse CVAE(tf.keras.Model):

def __init__(self, latent_dim):

super(CVAE, selbst).__init__()

self.latent_dim =latent_dim

self.inference_net =tf.keras.Sequential(

[

tf.keras.layers.InputLayer(input_shape=(28, 28, 1)),

tf.keras.layers.Conv2D(

filter=32, kernel_size=3, strides=(2, 2), aktivierung='relu'),

tf.keras.layers.Conv2D(

filter=64, kernel_size=3, strides=(2, 2), aktivierung='relu'),

tf.keras.layers.Flatten(),

# Keine Aktivierung

tf.keras.layers.Dense(latent_dim + latent_dim),

]

)

self.generative_net =tf.keras.Sequential(

[

tf.keras.layers.InputLayer(input_shape=(latent_dim,)),

tf.keras.layers.Dense(Einheiten=7*7*32, Aktivierung=tf.nn.relu),

tf.keras.layers.Reshape(target_shape=(7, 7, 32)),

tf.keras.layers.Conv2DTranspose(

filter=64,

kernel_size=3,

Schritte=(2, 2),

padding="SAME",

activation='relu'),

tf.keras.layers.Conv2DTranspose(

filter=32,

kernel_size=3,

Schritte=(2, 2),

padding="SAME",

activation='relu'),

# Keine Aktivierung

tf.keras.layers.Conv2DTranspose(

filter=1, kernel_size=3, Strides=(1, 1), padding="SAME"),

]

)

@tf.function

def sample(self, eps=None):

wenn eps None ist:

eps =tf.random.normal(shape=(100, self.latent_dim))

return self.decode(eps, apply_sigmoid=True)

def encode(self, x):

mean, logvar =tf.split(self.inference_net(x), num_or_size_splits=2, axis=1)

Rückgabewert, logvar

def reparametrieren(self, mean, logvar):

eps =tf.random.normal(shape=mean.shape)

Rückgabe eps * tf.exp(logvar * .5) + Mittelwert

def decode(self, z, apply_sigmoid=False):

logits =self.generative_net(z)

wenn apply_sigmoid:

probs =tf.sigmoid(logits)

Rückgabeprobleme

Rückgabeprotokolle

Die beiden Code-Snippets bereiten unser Dataset vor und bauen unser Variations-Autoencoder-Modell auf. Im Modellcode-Snippet gibt es einige Hilfsfunktionen zum Codieren, Sampling und Decodieren.

Umparametrierung für die Berechnung von Gradienten

Es gibt eine Reparametrisierungsfunktion, die wir nicht besprochen haben, die aber ein sehr wichtiges Problem in unserem Variations-Autoencoder-Netzwerk löst. Denken Sie daran, dass wir während der Decodierungsstufe die latente Vektorcodierung aus einer Verteilung abtasten, die durch den vom Codierer erzeugten Mittelwert und Varianzvektor gesteuert wird. Dies erzeugt kein Problem bei der Vorwärtsausbreitung von Daten durch unser Netzwerk, verursacht jedoch ein großes Problem bei der Rückwärtsausbreitung von Gradienten vom Decoder zum Encoder, da der Abtastvorgang nicht differenzierbar ist.

Einfach ausgedrückt können wir keine Gradienten aus einer Sampling-Operation berechnen.

Ein netter Workaround für dieses Problem besteht darin, den Reparametrisierungstrick anzuwenden. Dies funktioniert, indem zuerst eine standardmäßige Gaußsche Verteilung von Mittelwert 0 und Varianz 1 erzeugt wird und dann eine differenzierbare Additions- und Multiplikationsoperation an dieser Verteilung mit dem Mittelwert und der Varianz, die vom Encoder generiert werden, durchgeführt wird.

Beachten Sie, dass wir die Varianz im Code in den Logarithmusraum umwandeln. Damit soll die numerische Stabilität gewährleistet werden. Der zusätzliche Verlustterm, der Kullback-Leibler-Divergenzverlust, wird eingeführt, um sicherzustellen, dass die von uns generierten Verteilungen so nah wie möglich an einer Standard-Gaußschen Verteilung mit Mittelwert 0 und Varianz 1 liegen.

Die Mittelwerte der Verteilungen auf Null zu setzen stellt sicher, dass die von uns generierten Verteilungen sehr nahe beieinander liegen, um Diskontinuitäten zwischen den Verteilungen zu vermeiden. Eine Varianz nahe 1 bedeutet, dass wir einen moderateren (d. h. nicht sehr großen und nicht sehr kleinen) Raum haben, um Codierungen zu generieren.

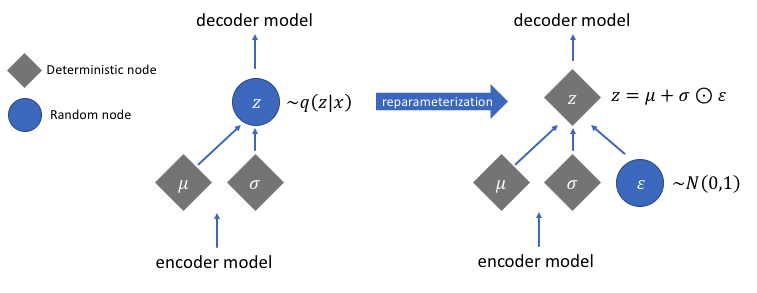
Bild mit freundlicher Genehmigung von Jeremy Jordan

Nach Durchführung des Reparametrisierungstricks ist die Verteilung, die durch Multiplizieren des Varianzvektors mit einer Standard-Gauß-Verteilung und Addieren des Ergebnisses zum Mittelwertvektor erhalten wird, der Verteilung sehr ähnlich, die unmittelbar durch den Mittelwert- und Varianzvektor gesteuert wird.

Einfache Schritte zum Erstellen eines Variations-Autoencoders

Lassen Sie uns dieses Tutorial abschließen, indem wir die Schritte zum Erstellen eines Variations-Autoencoders zusammenfassen:

1. Baue die Encoder- und Decoder-Netzwerke auf.
2. Anwenden eines Neuparametrierungstricks zwischen Encoder und Decoder, um eine Rückwärtsausbreitung zu ermöglichen.
3. Trainieren Sie beide Netzwerke durchgängig.

Den vollständigen oben verwendeten Code finden Sie auf der offiziellen TensorFlow-Website.

Ausgewähltes Bild von Chiman Kwan modifiziert