Kleinwinkelstreuung von nanoskaligen Fettfraktalen

Einführung

Viele hierarchische Strukturen, die auf Nano- und Mikroskala erzeugt werden, haben geometrische Eigenschaften, die bei Skalenerweiterungen invariant sind, Selbstähnlichkeit aufweisen und somit fraktale Eigenschaften aufweisen [1, 2]. Obwohl die jüngsten Fortschritte in den Materialwissenschaften und der Nanotechnologie die Herstellung verschiedener künstlicher deterministischer Fraktale im Nano-/Mikrobereich ermöglichen, mit einer exakten Selbstähnlichkeit [3–7], erzeugt die überwiegende Mehrheit der natürlichen Prozesse zufällige, statistisch selbstähnliche Fraktale. Eine gute Näherung in den Strukturstudien natürlicher fraktaler Formationen kann durch Rückgriff auf deterministische fraktale Modelle mit der gleichen fraktalen Dimension wie bei den zufälligen erfolgen. Dieser Ansatz wurde erfolgreich verwendet, um zu zeigen, dass die Übertragung über zufällige fraktale Oberflächen der Reaktion deterministischer Modellgeometrien sehr nahe kommt [8]. Durch die Einführung von Polydispersität in den Konstruktionsalgorithmus eines deterministischen Fraktales können ähnliche Kleinwinkelstreuungsintensitäten (SAS) erhalten werden, wie sie zufälligen Fraktalen entsprechen [9]. Darüber hinaus ist ein „deterministischer“ Ansatz rechnerisch effizienter, da er eine analytische Beschreibung verschiedener Eigenschaften wie fraktale Form, Strukturfaktoren und Trägheitsradius ermöglicht.

Eine der zuverlässigsten Methoden zur Bestimmung der strukturellen Eigenschaften von deterministischen und zufälligen Fraktalen [10, 11] ist die Wellenbeugung im Kontext der Kleinwinkelstreuung an nano- oder mikrostrukturierten Materialien unter Verwendung von Neutronen oder elektromagnetischen Wellen (x -Strahl, Licht usw.) [12]. Aus diesem Grund besteht eine der grundlegenden Aufgaben der theoretischen Beschreibungen in Verbindung mit experimentellen Bestimmungen in diesem Forschungsgebiet darin, den Zusammenhang zwischen der Struktur von Fraktalen und ihrem entsprechenden Beugungsspektrum bzw. Streuintensitätsverteilung vs. Streuwellenvektor aufzuzeigen. Viele experimentelle und theoretische Studien wurden in diese Richtung durchgeführt [13–21].

Unter Verwendung von theoretischen Standardberechnungen und Interpolation ist der Parameter, der aus dieser Art von experimentellen Messungen bestimmt wird, die massenfraktale Dimension D _m (siehe Anhang 1), mit D _m D _s , mit d −1<D _s <d . Wir haben mit d . bezeichnet die euklidische Dimension, in die das Fraktal eingebettet ist. Die massenfraktale Dimension beschreibt die Art und Weise, wie die Masse M (r ) variiert, wenn es in eine Scheibe mit dem Radius r . eingebettet ist . Der erhaltene Massenradius Beziehung \(M(r)\propto r^{D_{\mathrm {m}}}\) führt zum Verhalten der Streuintensität \(I(q)\propto q^{-D_{\mathrm {m} }}\). Offensichtlich D _m kann mit dem Exponenten der Potenzgesetzabhängigkeit der Streuintensität als Funktion des Streuwellenvektors q . identifiziert werden [18, 22]. Je höher der Wert von D _m , desto kompakter ist die Struktur. In ähnlicher Weise gehorcht im Fall eines Oberflächenfraktals seine Oberflächenverteilung \(S(r)\propto r^{2-D_{\mathrm{s}}}\), und somit \(\phantom {\dot{ i}\!}I(q)\propto q^{-(2\mathrm{d}-D_{\mathrm{s}})}\) [19, 23]. Arbeiten im dreidimensionalen euklidischen Raum, D _s nähert sich dem Minimum von zwei, wenn die Oberfläche fast vollkommen glatt ist. Es neigt zu maximal drei, wenn es so gefaltet ist, dass es den Raum fast vollständig ausfüllt.

Viele experimentelle Beugungsintensitäten von verschiedenen chemisch synthetisierten und biologischen Systemen sind auf einer doppelten logarithmischen Skala durch eine Abfolge von Potenzgesetzzerfällen gekennzeichnet, die durch Bereiche konstanter Intensität verschachtelt sind. Dieses Verhalten lässt sich für einige Polymergele [24], Glykosidhydrolase für Cellobiosesubstrat [25], Polyelektrolytkomplex-Koazervate [26] oder nanoporösen Kohlenstoff [27] nachweisen. Obwohl das klassische Beaucage-Modell [28] grundlegende strukturelle Informationen über diese Systeme liefern kann (dh Massen- oder Oberflächenfraktaldimensionen und die Gesamtgröße jeder Strukturebene), ist aufgrund der großen Anzahl von Konfigurationen, die ein fester Wert der fraktalen Dimension. Dieses Problem wurde kürzlich teilweise von Cherny et al. [29] im Kontext der Small Angle Scattering (SAS)-Modelle. Es wurde gezeigt, dass für deterministische Massenfraktale mit einer einzigen Skala zusätzliche Informationen erhalten werden können, wie z. Dieser Ansatz wurde außerdem erfolgreich verwendet, um neue Modelle für fette Fraktale zu entwickeln, wenn Abfolgen von Potenzgesetzzerfällen in den Streuverteilungen vorhanden sind. Es kann auf Strukturen angewendet werden, bei denen die Gesamtgröße der Grundkomponenteneinheiten in der gleichen Größenordnung wie die Abstände zwischen ihnen ist [30, 31].

Das in diesem Artikel vorgestellte theoretische Modell kombiniert frühere Modelle, um ihre Anwendbarkeit zu erweitern. Es beschreibt Abfolgen von Potenzgesetzzerfällen mit willkürlich abnehmenden Werten der Streuexponenten, und durch Bereiche konstanter Intensität verschachtelt. Unser Modell ist auch in der Lage, detailliertere Informationen über jede Strukturebene im Nano-/Mikrofraktal zu liefern. Zu diesem Zweck betrachten wir ein fettes Fraktal, repräsentiert durch ein zweidimensionales deterministisches Massenfraktal mit einem Skalierungsfaktor, der von der Iteration abhängig ist, aber mit nicht verschwindender Oberfläche im Grenzbereich einer großen Anzahl von Iterationen, also mit einem positiven Lebesgue-Maßnahme. Wir leiten analytische Ausdrücke der fraktalen Form- und Strukturfaktoren ab und zeigen, wie die fraktalen Dimensionen und Skalierungsfaktoren auf jeder Strukturebene bestimmt werden.

Theoretischer Hintergrund

Betrachtet man ein Array ähnlich orientierter, identischer Beugungsaperturen, hier mit Σ . bezeichnet , enthält N transparente Regionen, gekennzeichnet mit j , muss eine Summation über die von jeder Apertur erhaltenen Amplituden berücksichtigt werden. Die bekannte Frequenzverteilung der Beugungsamplitude einer einzelnen Apertur (Gl. (37) in Anhang 2) kann also umgeschrieben werden als [32]:

Die Koordinaten eines Punktes im lokalen Rahmen des j Blende sind (x _j ,y _j ) und T (x,y ) stellt die individuelle Transmissionsfunktion dar, die jedem transparenten Bereich entspricht. Man kann Summation mit Integration austauschen, weil in unserem Fall die Aperturen durch dieselbe individuelle Verteilungsfunktion beschrieben werden, so dass Gl. (1) kann umgeschrieben werden als:

Der Integralfaktor aus der vorherigen Gleichheit stellt die Fourier-Transformation der Verteilungsfunktion jeder der identischen Aperturen dar, wie oben erwähnt. Diese Amplitude wird durch den die Summation enthaltenden Faktor moduliert, der die Fourier-Transformation von Dirac-Delta-Verteilungen der Form \(A_{\delta}~=~\sum_{j~=~1}^{N}(x~ -~x_{j})(y~-~y_{j})\). Somit wird auch die räumliche Verteilung der Aperturen innerhalb des Arrays berücksichtigt. Somit ist Gl. (2) kann in der Form umgeschrieben werden, die als Array-Theorem [32] bekannt ist:

Die Intensitätsverteilung des gebeugten Bildes in der Fourier-Ebene wird zu:

Erwartungsgemäß entspricht der erste Faktor im Produkt der Streuintensität eines einzelnen Lochs, während der zweite die Verteilung dieser Löcher innerhalb der Beugungsapertur aufzeigt Σ . Diese Größen werden auch als Formfaktor F . bezeichnet (p,q ) bzw. der Strukturfaktor S (p,q ). Aus diesem Grund werden die in der gesamten Arbeit erhaltenen Ergebnisse mit der folgenden Form der Streuintensität ausgedrückt:

Fat Fractal Model and Method

Die detaillierte Vorgehensweise zur Konstruktion eines dünnen (regulären) Cantor-Fraktales ist bekannt [33]. Hier wird nur das Hauptbauverfahren zusammengefasst. Es wird ein Ansatz von oben nach unten gewählt. Beginnend mit einem Anfangsquadrat (oder einer anderen euklidischen Form) der Kante l ₀ (bei m =0), deren Mittelpunkt mit dem Ursprung des kartesischen Koordinatensystems zusammenfällt und Kanten parallel zu den Koordinatensystemachsen liegen, erfüllt jeder Punkt im Quadrat die Bedingungen −l ₀ /2≤x l ₀ /2 und −l ₀ /2≤y l ₀ /2. Bei der ersten Iteration (m =1), wird das Quadrat in vier weitere Quadrate geteilt, mit Kantenlänge \(\beta_{\mathrm{s}}^{(1)}l_{0}\). Wir bezeichneten mit \(\beta_{\mathrm{s}}^{(1)} \equiv (1-\gamma_{1})/2\), mit \(0 <\beta_{\mathrm{ s}}^{(1)} <1/2\), der Skalierungsfaktor der ersten Iteration, und mit γ ₁ der Bruchteil der abgetragenen Länge an dieser Stelle, wie in Abb. 1 a, b) für m . zu sehen ist =1. Die Zahl zwischen (⋯), die als oberer Index erscheint, quantifiziert die Iterationszahl. Sie darf nicht als Exponent einer Potenzfunktion interpretiert werden. Hinsichtlich des Skalierungsfaktors sind die Positionen der vier Quadrate durch die Vektoren \(\boldsymbol{a}_{j}~=~\left\{\pm\beta_{\mathrm{t}}^{ (1)}l_{0}, \pm\beta_{\mathrm{t}}^{(1)}l_{0}\right\}\) mit allen möglichen Vorzeichenkombinationen, wobei \(\beta_{ \mathrm{t}}^{(1)}~=~\left (1-\beta_{\mathrm{s}}^{(1)}\right)/2\) wird verwendet, um Formulierungen weiter zu vereinfachen. Das Quadrat wurde aufgrund der Einfachheit der numerischen Berechnungen als Ausgangsform gewählt. Jede andere geometrische Form, beispielsweise ein Kreis, kommt in Betracht. Der Effekt der Wahl einer anderen Form wird nur in der Porod-Region des Formfaktors beobachtet, was den Rahmen dieses Papiers sprengen würde.

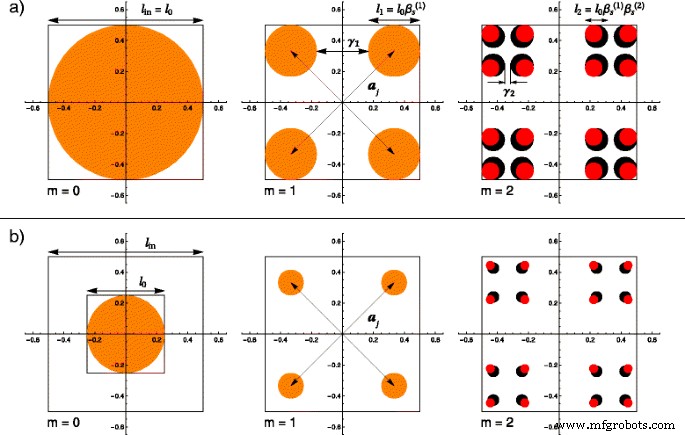
(Farbe online) Ein Vergleich zwischen regulären und fetten Fraktalen für die ersten beiden Iterationen, wobei die Grundform bei m =0 ist eine Scheibe mit dem Durchmesser l ₀ und die Fraktalgröße ist l _in :a l ₀ =l _in; b l ₀ =l _in /f , mit f =2. In beiden Fällen bei m =1 fallen die Strukturen wegen gleicher Skalierungsfaktoren \(\beta_{\mathrm{s}}^{(1)}\) zusammen. Beginnend mit m =2, das Fettfraktal hat einen größeren Skalierungsfaktor \(\left(\beta_{\mathrm {s}}^{(2)}> \beta_{\mathrm {s}}^{(1)}\ rechts)\), und daher haben Scheiben einen größeren Durchmesser (schwarze Scheiben ) als bei regulären Fraktalen (rote Scheiben ); a _j sind die Ortsvektoren und γ _ich sind die Bruchteile der entfernten Länge bei i Iteration

Die ersten beiden oben beschriebenen Schritte werden auch bei der Konstruktion der klassischen Version eines Fettfraktals angewendet, für Iterationen m =0 und m =1. Deshalb fallen diese beiden Strukturen bisher zusammen. Um das Fettfraktal zu erhalten, eine Modifikation des bei Iteration verwendeten Algorithmus m =1 muss durchgeführt werden, indem ein anderer Skalierungsfaktor bei m . gewählt wird =2, \(\beta_{\mathrm{s}}^{(2)} \equiv (1 - \gamma_{2})/2\). Wendet man den gesamten Algorithmus im Limit einer hohen Anzahl von Iterationen an [34, 35], erhält man wieder die klassische Version eines Fettfraktals. Aus der Konstruktion geht klar hervor, dass die reguläre Version des Fraktals wiederhergestellt wird, wenn die Skalierungsfaktoren bei jeder Iteration gleich \(\beta_{\mathrm{s}}^{(1)}~=~ \beta_{\mathrm{s}}^{(2)}~=~\cdots =\beta_{\mathrm{s}}^{(m)}\).

Um das konstante Plateau zwischen zwei Potenzgesetzzerfällen im Verhalten der SAS-Intensität zu erhalten, müssen wir berücksichtigen, dass die Abstände zwischen den Streueinheiten viel größer sind als ihre Gesamtgröße. Ein solcher Ansatz wurde erstmals im Zusammenhang mit Oberflächenfraktalmodellen verwendet [36, 37]. Unter Berücksichtigung des Verhältnisses f des Gesamtabstands zwischen den Streueinheiten l _in und ihre Gesamtgröße l ₀ , man hat:

Für Streuexperimente, die Plateaus konstanter Intensität zwischen zwei fraktalen Regionen zeigen, sind Werte von f ≫1 sollte gewählt werden. Bei Oberflächenfraktalen den Wert von f . erhöhen führt zu einer besseren Übereinstimmung zwischen der gesamten SAS-Intensität einerseits und der Näherung unabhängiger Streueinheiten andererseits [36, 37].

Anhand der obigen Überlegungen können die Unterschiede zwischen regulären und fetten Fraktalen beschrieben werden. Der Einfluss des Faktors f , oben eingeführt, auch visualisiert werden. Aus diesem Grund veranschaulichen wir in Abb. 1 den Vergleich grafisch anhand einer Scheibe mit dem Radius r ₀ l ₀ /2=l _in /(2f ) als unsere Grundform. Die Ergebnisse der ersten beiden Iterationen, die in jeder Zeile von Abb. 1 angezeigt werden, stellen die Strukturen dar, die für ein reguläres Fraktal (durch rote Scheiben markiert) und ein fettes Fraktal (dargestellt als schwarze Scheibe) erhalten wurden, die auch vollständig überlagert werden können ( als orangefarbene Scheiben markiert). In der mit Abb. 1 a bezeichneten Zeile ist der Faktor f wird als gleich der Einheit angesehen, so dass die klassischen Konstruktionen und fraktalen Formen erhalten werden. Die zweite Reihe der Abbildung, mit 1 b bezeichnet, zeigt den Einfluss des oben dargestellten Faktors. In diesen Berechnungen haben wir den willkürlichen Wert von f . gewählt =2. Man beobachtet, dass bei Iterationen m =0 und m =1, sowohl im a- als auch im b-Fall sind die erhaltenen Strukturen der regulären und dicken Cantor-Mengen identisch und vollständig überlagert. Dies ist aufgrund des gemeinsamen Skalierungsfaktors zu erwarten. Wie jedoch im letzten Bildpaar aus Abb. 1 zu sehen ist, beginnend mit m =2, sind die Radien der Scheiben des Fettfraktals größer, weil sein Skalierungsfaktor \(\beta_{\mathrm{s}}^{(2)}\) per Definition größer ist als der des regulären. Im letzten Bild aus Abb. 2 b ist die Größe der Scheiben aufgrund des nicht einheitlichen Wertes des Faktors f . viel kleiner als im Gegenstück aus Abb. 2 a .

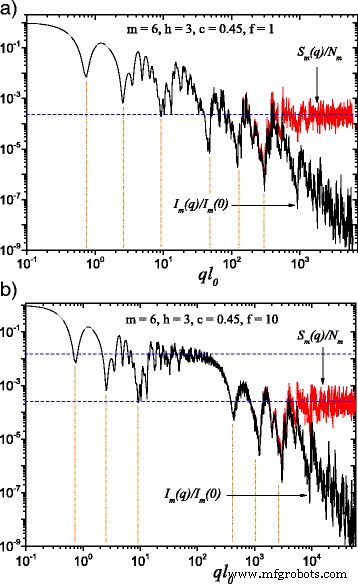
(Farbe online) Ein Vergleich der Streuintensität nach Gl. (22) (schwarze Kurven ) und Strukturfaktor gegeben durch Gl. (24) (rote Kurven ) um m =6 und über Orientierungen gemittelt nach Gl. (25). Hier, h =3 (d. h. der Skalierungsfaktor wird für drei aufeinanderfolgende Iterationen konstant gehalten), während die Grundform bei der Berechnung der Streuintensität ein Quadrat der Kantengröße l . ist ₀ :a l ₀ =l _in; b l ₀ =l _in /f (mit f =10). Wenn f ≠1, erscheint zwischen den beiden verallgemeinerten Potenzgesetz-Zerfällen ein Plateau konstanter Intensität (Abb. 2 b). Horizontale Linien bezeichnen die Asymptote des Strukturfaktors ≃1/N _m , während die Minimapositionen nach Gl. (26)

Um die Potenzgesetze selbst zu erhalten, muss man das klassische Fettfraktalmodell weiter verallgemeinern. Dies geschieht unter Berücksichtigung der Tatsache, dass die Skalierungsfaktoränderungen nicht bei jeder einzelnen Iteration vorgenommen werden, sondern jede zweite, dritte, oder allgemein gesagt alle h te Iteration. Der Anteil der entfernten Längen bei m Iteration ist:

mit 0<c <1. Die Funktion p _m ist definiert als:

für jeden positiven ganzzahligen Wert von m , mit h =1,⋯,m , wobei die Bodenfunktion ⌊⋯ ⌋ verwendet wurde. Somit entspricht der Skalierungsfaktor dem m Iteration ist gegeben durch:

Es ist jetzt klar, dass der Zweck der Funktion p _m besteht darin, den Skalierungsfaktor für h . konstant zu halten Iterationen (h <m ).

Die Komponenten der Positionsvektoren jedes Quadrats können geschrieben werden als:

während die Kantenlänge jedes Quadrats gegeben ist durch:

Der Faktor f ist in der Formel der Länge l . zu verwenden ₀ zu berücksichtigen, dass für Iterationen zwischen den (h +1) und m Mai nimmt die Größe der Quadrate in Bezug auf die Abstände zwischen ihnen ab:

wo h <m . Die Anzahl der Quadrate bei jeder Iteration beträgt:

Somit hat man auf jeder Skala, die als Iteration mit konstantem Skalierungsfaktor betrachtet wird, eine andere fraktale Dimension, die durch [29, 38, 39] gegeben ist:

Im Grenzfall einer großen Anzahl von Iterationen beträgt die fraktale Dimension der konstruierten fraktalen Menge [34]:

das ist der erwartete Wert für ein zweidimensionales Fettfraktal. Schließlich, wenn a _ich ist die relative Fläche, die bei i . entfernt wurde Iteration, dann \(\prod_{i=1}^{m}(1-a_{i})> 0\) falls \(\sum_{i=1}^{\infty} a_{i} <\infty \), und somit erfüllt das Modell die Definition und die Eigenschaften von Fettfraktalen [35].

Ergebnisse und Diskussion

Nach dem Babinet-Prinzip können wir schließen, dass bei m Iteration sind die Aperturen im Gitter die verbleibenden Quadrate im Fraktal, während die entfernten Teile für die Strahlung undurchlässig werden.

Monodisperse Streuintensität und Strukturfaktor

Um den analytischen Ausdruck der Streuintensität für das fette Cantor-Fraktal abzuleiten, schreiben wir zunächst die Rekursion der Gittertransmission für eine willkürliche Iteration entsprechend 1D Fall. Um m =0, wir haben

Unter Berücksichtigung des Konstruktionsalgorithmus des Fraktals ist die Transmission nach der ersten Iteration gegeben durch:

$$ \begin{aligned} T_{1}(l_{1}, x,) =T_{0}(l_{1}, x) \ast \delta\left(\frac{x-l_{0}\ beta_{\mathrm{t}}^{(1)}}{l_{1}}\right) + \\ T_{0}(l_{1}, x) \ast \delta\left(\frac{x +l_{0}\beta_{\mathrm{t}}^{(1)}}{l_{1}}\right),~~~~~~~~~~~~ \end{aligned} $$ (17)

wo δ (x −a ) ist die eindimensionale Dirac-Delta-Verteilung bei x =a . Das Symbol ∗ repräsentiert den Faltungsoperator. Daher bei m Iteration können wir schreiben:

$$ \begin{ausgerichtet} T_{m}(l_{m}, x) =T_{m-1}(l_{m}, x) \ast \delta\left(\frac{x-u_{m} }{l_{m}} \right) + \\ T_{m-1}(l_{m}, x, y) \ast \delta\left(\frac{x+u_{m}}{l_{m }} \right),~~~~~~~~~~~~ \end{ausgerichtet} $$ (18)

wobei \(u_{m}~=~l_{0}\beta_{\mathrm {t}}^{(m)}\prod_{j=1}^{m-1}\beta_{\mathrm {s}}^{(j)}\). Durchführen einer Fourier-Transformation an Gl. (18) findet man, dass die Streuamplitude bei m Iteration ist:

$$ A_{m}(p)=2^{m}\frac{\sin(\pi p l_{m})}{\pi p l_{m}}\prod\limits_{i=1}^{ m}\cos(2\pi p u_{i}). $$ (19)

Seit dem 2D Das Fettfraktalmodell ist ein direktes Produkt zweier eindimensionaler Fettfraktale, seine Fourier-Transformation kann als Produkt zweier eindimensionaler Fourier-Transformationen geschrieben werden. Daher kann die zweidimensionale Streuamplitude geschrieben werden als:

$$ A_{m}(p,s)\äquiv. A_{m}(p) A_{m}(s), $$ (20)

und somit

$$ \begin{ausgerichtet} A_{m}(p, s) =N_{m}\frac{\sin(\pi p l_{m})}{\pi p l_{m}}\frac{\sin (\pi s l_{m})}{\pi s l_{m}} \times \\\prod\limits_{i=1}^{m}\cos(2\pi p u_{i})\cos (2\pi s u_{i}), \end{ausgerichtet} $$ (21)

damit wird die Streuintensität:

$$ \begin{ausgerichtet} I_{m}(p, s) =\left(\frac{\sin(\pi p l_{m})}{\pi p l_{m}}\frac{\sin( \pi s l_{m})}{\pi s l_{m}} \right)^{2} \times \\ N_{m}^{2} \left(\prod\limits_{i=1}^ {m}\cos(2\pi p u_{i})\cos(2\pi s u_{i}) \right)^{2}. \end{ausgerichtet} $$ (22)

Der erste Faktor in der vorherigen Gleichung, der die Beugungsintensität aufgrund des Formfaktors darstellt, wie in Gl. (5):

$$ F_{m}(p, s) =\left(\frac{\sin(\pi p l_{m})}{\pi p l_{m}}\frac{\sin(\pi s l_{ m})}{\pi s l_{m}} \right)^{2}, $$ (23)

entspricht der Streuintensität, die von einem einzelnen Quadrat der Kante l . erhalten wird _m . Der zweite Faktor, der die Beugungsintensität aufgrund des Strukturfaktors repräsentiert, wie in Gl. (5):

$$ S_{m}(p, s) =N_{m}^{2}\left(\prod\limits_{i=1}^{m}\cos(2\pi p u_{i})\cos (2\pi s u_{i}) \right)^{2}, $$ (24)

beschreibt die Verteilung der Quadrate. Die gesamte Streustrahlungsintensität ist das Produkt von F _m (p,s ) und S _m (p,s ).

Der Potenzgesetzabfall der Intensität, wie er in Gl. (22), wird erhalten, nachdem der Durchschnitt über alle Orientierungen durchgeführt wurde [29]. Bei gleicher Wahrscheinlichkeit für jede Orientierung kann der Durchschnitt im Fall von zweidimensionalen Fraktalen berechnet werden, indem über alle Richtungen des Streuvektors integriert wird q =(p,s ):

$$ \langle f(p, s) \rangle =\frac{1}{2\pi} \int_{0}^{2\pi}f(q,\phi)\mathrm{d}\phi, $ $ (25)

wo p =q cosϕ und s =q Sündeϕ . Somit ist die Streuintensität I (q ) erhält man als Funktion des Impulsübertragungsmoduls q ≡|q |.

Denn nach der Definition des Strukturfaktors gilt \(S_{m}(0)~=~N_{m}^{2}\), wobei N _m ist die Anzahl der Quadrate, wie in Gl. (13), das Standardverfahren der Normalisierung S _m (0) =1 kann übernommen werden, wie in [11, 29] beschrieben.

Die berechneten Ergebnisse für die monodisperse Streuintensität I _m (q ) und Strukturfaktor S _m (q ), mit m =6, sind in Abb. 2 für das klassische Fettfraktal (f =1 in Abb. 2 a) und für das in dieser Arbeit entwickelte erweiterte Fettfraktalmodell (f =10 in Abb. 2 b). Um die Abb. 2 b zu erhalten, betrachteten wir h =3 so dass der Skalierungsfaktor \(\beta_{\mathrm{s}}^{(1)}\) der ersten drei Iterationen konstant gehalten wurde, dann hatte er einen anderen konstanten Wert \(\beta_{\ mathrm {s}}^{(2)}\) für die nächsten drei Iterationen. Wie erwartet, in beiden Fällen (für f =1 und f =10), können die Unterschiede zwischen Streuintensität einerseits und Strukturfaktor andererseits beobachtet werden, wenn \(q\gtrsim 1/l_{m}\). In diesem Bereich hat die Streuintensität einen Potenzgesetzabfall I (q )∝q ⁻³ . Der Strukturfaktor hat einen asymptotischen Wert, der zu 1/N . tendiert _m , dargestellt durch die horizontale Linie in Abb. 2 a oder die untere horizontale Linie in Abb. 2 b [29, 33].

Eine Abfolge von zwei verallgemeinerten Potenzgesetzzerfällen, erkennbar als Überlagerung von Maxima und Minima, über einem einfachen Potenzgesetzzerfall, ist in Abb. 2 a zu sehen. Aber in Abb. 2b, ein Bereich mit ungefähr konstanter Intensität, im Bereich 20≲ql ₀ ≲100, klar unterschieden werden kann, eingeschlossen von den zwei aufeinanderfolgenden verallgemeinerten Potenzgesetzzerfällen. Dies liegt an der Verringerung der Quadratgröße um eine Größenordnung (f =10) im Vergleich zu den Abständen zwischen ihnen. Dieser Bereich, der in Abb. 2b um die obere horizontale Linie beobachtbar ist, hat die Asymptote 1/N ₃ , der gleiche wie der Strukturfaktor des klassischen Fettfraktals, zeigt ein ähnliches Verhalten wie bei der Betrachtung nur der ersten drei Iterationen.

Außerdem ist in Fig. 2 zu sehen, dass die Anzahl der Minima bei jeder Skala mit der Anzahl der Iterationen des konstanten Skalierungsfaktors übereinstimmt. Diese Minima treten auf, wenn die Strahlung, die durch verschiedene Quadrate innerhalb des Fraktals geht, interferiert und gegenphasig ist, und somit die am häufigsten angetroffenen Abstände zwischen den Mittelpunkten von Quadraten (2u _m ) sind gleich mit π /q . Deshalb erhält man die ungefähren Positionen der Minima aus der Beziehung:

$$ q_{i} \simeq \frac{\pi}{2 u_{i}},~~~~i=1, \cdots, m $$ (26)

in Fig. 2 durch vertikale Linien angedeutet. Bei den ersten sechs Iterationen beobachtet man eine recht gute Übereinstimmung zwischen den mit Gl. (26), und diejenigen, die in der Streuintensität oder dem Strukturfaktor gefunden werden. Diese Näherung kann bei höheren Iterationen weniger genau sein, sobald die Iterationszahl einen bestimmten Wert überschreitet, da in diesen Fällen immer mehr Distanzen mit den am häufigsten vorkommenden vergleichbar sind. Trotzdem wird diese Näherung in der Praxis recht gut funktionieren, wo man kaum erwarten kann, mehr als vier oder fünf solcher Minima zu unterscheiden.

Für jede einzelne Skala in einem bestimmten Bereich 1/(2u _ich )≲q ≲1/(2u _{ich +1} ), wird das Beugungsmuster nur durch die Interferenz der i . erzeugt fraktale Iteration. Damit kann gezeigt werden, dass innerhalb dieses Intervalls die Funktionen I _m (q )q ^D und S _m (q )q ^D sind logarithmisch [29], wobei D ist die fraktale Dimension, die einer gegebenen Skala entspricht. Insbesondere für die in den Fign. 2 und 3, die Funktionen I _m (q )q ^−1.1 und S _m (q )q ^−1.1 sind logarithmisch mit der Periode \(1/\beta_{\textrm{s}}^{(1)}\) für die ersten drei Iterationen, während I _m (q )q ^−1,51 und S _m (q )q ^−1,51 sind logarithmisch periodisch mit \(1/\beta_{\textrm{s}}^{(2)}\) für die zweite Gruppe von drei Iterationen.

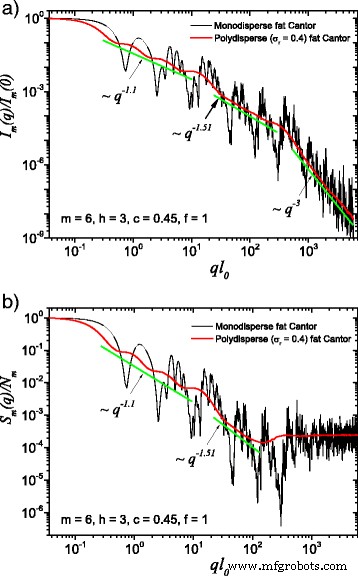
(Farbe online) Ein Vergleich zwischen monodispersen und polydispersen Systemen:a Streuintensität (Gl. (22)); b Strukturfaktor (Gl. (24)), gemittelt über alle Orientierungen des Fraktals, nach Gl. (25). Hier, f =1, m =6, h =3 (d. h. der Skalierungsfaktor wird für drei aufeinanderfolgende Iterationen konstant gehalten), und die Grundform ist ein Quadrat der anfänglichen Kantenlänge l ₀ =l _in . In beiden Fällen verwischt die Polydispersität monodisperse Streukurven und die fraktalen Dimensionen können auf jeder Strukturebene wiederhergestellt werden

Ähnlich wie bei deterministischen Massenfraktalen ist Gl. (26) kann verwendet werden, um mehrere strukturelle Parameter zu erhalten, die Fettfraktale charakterisieren. Erstens stimmt die Gesamtzahl der Minima mit der Gesamtzahl der fraktalen Iterationen überein. Abbildung 2 zeigt, dass das Fraktal aus drei Iterationen mit Skalierungsfaktor \(\beta_{\textrm{s}}^{(1)}\) und drei Iterationen mit Skalierungsfaktor \(\beta_{\textrm{s}) besteht }^{(2)}\). Zweitens aus der Periodizität dieser Minima (oder aus der Periodizität von I _m (q )q ^D und S _m (q )q ^D ) können die Skalierungsfaktoren wiederhergestellt werden. In Abb. 2 b kann der Skalierungsfaktor \(\beta_{\textrm{s}}^{(1)}\) aus der Periodizität der Minima bei ql ₀ ≃7,25 und 90, während der Skalierungsfaktor \(\beta_{\mathrm{s}}^{(2)}\) aus der Periodizität der Minima bei ql ₀ ≃400,1000 und 2500. Darüber hinaus kann die Länge des Zwischenplateaus zwischen fraktalen Regionen als Hinweis auf das Verhältnis verwendet werden (f ) der Abstände zwischen Streueinheiten und ihrer Gesamtgröße. In Abb. 2 b entspricht dieser Bereich 13≲ql ₀ ≲130.

Polydisperse Streuintensität und Strukturfaktor

In diesem Teil unserer Arbeit können wir nun berücksichtigen, dass die Gittergrößen einer Verteilungsfunktion D . gehorchen _N (l ₀ ), so definiert, dass D _N (l ₀ )dl ₀ gibt die Wahrscheinlichkeit an, dass die Größe des fraktalen Gitters im Intervall liegt (l ₀ ,l ₀ +dl ₀ ). Dieser Schritt führt Polydispersität in unser Fettfraktalmodell ein. Wir veranschaulichen dies, indem wir eine logarithmische Normalverteilung wählen:

$$ D_{\mathrm{N}}(l_{0}) =\frac{1}{\sigma l_{0} (2\pi)^{1/2}}e^{-\frac{\left (\log(l_{0}/\mu)+\sigma^{2}/2\right)^{2}}{2\sigma^{2}}}, $$ (27)

mit relativer Varianz \(\sigma_{\mathrm{r}} =\left(\left\langle l_{0}^{2} \right\rangle_{D} - \mu^{2}\right)^ {1/2}/\mu\), Mittelwert μ =〈l ₀ 〉 _D , and variance \(\sigma =\left (\log \left (1+\sigma _{\mathrm {r}}^{2}\right)\right)^{1/2}\). Using Eqs. (21) and (27) one obtains the polydisperse intensity averaged over the distribution function:

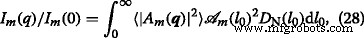
wo 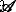is the corresponding area at m th iteration. The structure factor is calculated in a similar manner, but without the term 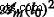[29].

The computed results in the case of polydisperse (red curves) and monodisperse (black curves) scattering intensities (labeled by a) and structure factors (labeled by b) can be seen in Figs. 3 and 4. The difference between them is given by the value of the f Faktor. In Fig. 3, the classical construction of a fat fractal was used so that f =1, while taking into account the smaller sizes of the basic units leads to the choice of f =10 in Fig. 4. Polydispersity is calculated for a relative variance of σ _r =0.4. It can be seen that the oscillations are smeared out, the overall amplitude decreases, so that the scattering curves become smoother [29, 40]. However, for this particular value of σ _r , the positions of main minima and maxima are still observable.

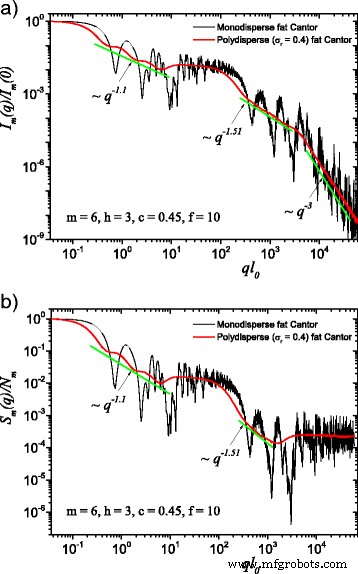
(Color online) A comparison between monodisperse and polydisperse systems:a scattering intensity (Eq. (22)); b structure factor (Eq. (24)), averaged over all orientations of the fractal, according to Eq. (25). Here, f =10 (and thus, a region of constant intensity appears at about 20≲ql ₀ ≲100), m =6, h =3 (i.e., the scaling factor is kept constant for three consecutive iterations), and the basic shape is a square of initial edge length l ₀ =l _in . For both cases, the polydispersity smears out monodisperse scattering curves, and the fractal dimensions can be recovered at each structural level

More generally, for small values of σ _r (i.e., small enough that the oscillations are observable), the estimation given by Eq. (26) can be still used. Hence, the number of fractal iterations, the scaling factor at each structural level, the ratio of the distances between scattering units, and their overall size can be recovered. When σ _r is increased to high enough values so that oscillations are completely smeared out, the scattering curves become simple power-law decays. Since we used a narrow bell-shaped distribution, the scattering exponent is preserved. Moreover, it gives, for each power-law decay, the fractal dimension of that particular structural level. This is in good agreement with the theoretical estimation of Eq. (14). This is also in accordance with experimental setups, where almost every scattering curve has a certain degree of polydispersity. Thus, our developed fat fractal model, with an interleaved region of constant intensity, recovers the fractal dimension at each structural level from polydisperse experimental data.

Schlussfolgerungen

In this article, we suggest a theoretical model that generalizes the standard one for nanoscale fat fractals. It is characterized by the fact that the initial edge size of the elementary unit shape is taken to be much smaller than that of the overall size of the fractal, and thus, much smaller than the distances between the elementary units inside the fractal. Figure 1 b illustrates the basic model, when a quotient of 1/2 is considered in-between these quantities, respectively.

Based on this model, an analytical formula is calculated and presented, in Eq. (22) for the scattering intensity and in Eq. (24) for the structure factor. Averaging over all possible orientations is done according to Eq. (25). These averaged quantities are characterized, on a double logarithmic scale, by the presence of two structural levels, and thus by two power-law decays interleaved by a region of constant intensity, represented by a plateau, as seen in Figs. 2 b and 4. This plateau coincides with the asymptotic region of the structure factor of the fat fractal, as if we would have considered only the contribution from the first structural level, when the scaling factor was kept constant. The asymptotic values of the plateaus can be used to obtain the number of scattering units for each structural level. The length of the plateau is controlled by the value of f . The power-law decays encompassing the plateau are obtained by keeping constant the scaling factors for a finite number of iterations, in our case, as an example, for three out of a total of six. The slope of the second power-law decay is higher because the values of scaling factors, by definition, increase at each structural level, and this is confirmed by our numerical computations, as can be seen in Figs. 2, 3, and 4.

We also described the polydisperse case of the fat fractal model. Here, the sizes of the composing units obey, as an example, a log-normal distribution function. We obtained smoothed curves for the scattering intensities and structure factors. The monodisperse scattering curves as well as the polydisperse ones, with small enough values of the relative variance, allow to obtain the scaling factors at each structural level, while the scattering exponents in the polydisperse curve give the fractal dimensions at each structural level. The chosen value of 0.4 for the relative variance is meant to illustrate the case in which one can still observe some minima in the scattering characteristics, and the curves still retain a shape close to power-law decays.

The results obtained in the framework of the suggested model can be used to reveal structural properties of fractal materials characterized by a regular law of changing of the fractal dimensions. The proposed model is also a very versatile one because it can be extended to include other features such as different shapes of the elementary unit, more than two structural levels, or it can be adapted to work in other Euclidean dimensions. These results are useful for a detailed description of experimental diffraction data in the context of small-angle scattering obtained from various complex nano- and micro- scaled hierarchical structures.

Appendix

fractal dimension

Mass and, respectively, surface fractal dimensions are probably the most important quantities that characterize a fractal. Actually, we will deal only with deterministic mass fractals, and we shall refer to mass fractal dimension, simply as the fractal dimension (D _m ).

In general terms, the mass-radius relation can be rewritten as [2]:

where the scaling law correction A (r ) tends to a constant value if r →∞ .

If it is known a priori that the structure is a fractal in the high number limit, the fractal dimension can be found straight from the first iteration. To illustrate this procedure, let us consider a fractal of size l ₀ , composed of k elementary units at the first iteration, each of size β _s l ₀ , where β _s is a scaling factor. Since the mass-radius relation, given by Eq. (29), is equivalent with the scale-invariance relation [2]:

one can write M (l ₀ )=kM (β _s l ₀ ). Unter Verwendung von Gl. (29), one obtains a direct method to compute the fractal dimension, via:

fraunhofer diffraction and the array theorem

Let us consider a two-dimensional diffracting aperture Σ , laid in the (x,y ) plane, illuminated in the positive z Richtung. In an observation plane (u,v ), parallel to Σ , the complex-valued amplitude of the obtained diffraction image, computed using the framework of scalar theory of diffraction, according to the Huygens-Fresnel principle, can be written as [41]:

In the previous formula, \(r =\sqrt {z^{2}+(u-x)^{2}+(v-y)^{2}}\) is the distance between two arbitrarily points taken, respectively, from the plane containing Σ and from the observation plane. For the Fraunhofer diffraction model to be applicable, this distance must satisfy the condition of being much bigger than the wavelength λ .

Performing a binomial expansion of the square root in Eq. (32) and retaining only the first two terms, one obtains [41]:

This approximation leads to the Fresnel diffraction integral:

where the prefactor P (u,v ) is given by

und k =2π /λ . Considering, in addition, that the condition z ≫k Max(x ² +y ² )/2 is satisfied, one has \(\text {Exp}{\left (\frac {k}{2z}(x^{2}+y^{2})\right)} \simeq 1\). Rewriting Eq. (34), the Fraunhofer approximation becomes:

Denoting the spatial frequencies with p =u /(λ z ) and s =v /(λ z ) and ignoring the multiplicative phase factor P (u,v ) preceding the integral in Eq. (36), the amplitude becomes simply the Fourier transform of the distribution of the Σ aperture. Considering that the illumination is made using a monochromatic, unit-amplitude plane-wave, at normal incidence, and that the field distribution across the aperture is equal to its transmission function T (x,y ), one obtains the frequency distribution of the diffraction amplitude in the phase space: