Schätzung der Superkondensator-Energiespeicherung basierend auf fraktionierten Differentialgleichungen

Hintergrund

Heute sind Superkondensatoren die Hauptkomponenten vieler Geräte und Systeme, z. B. Notstrom- und Stromrückgewinnungssysteme sowie Automobilanwendungen, Hybridfahrzeuge und viele andere. Die Fähigkeit, Ladung ohne chemische Reaktionen zu akkumulieren, führt dazu, dass solche Elemente im Vergleich zu typischen Batterien eine hundertmal höhere Anzahl von Lade-/Entladezyklen aufweisen [1]. Darüber hinaus machen sie hohe Lade-/Entladeraten effektiv für Anwendungen in Energierückgewinnungssystemen, die beispielsweise im Verkehr oder in erneuerbaren Energiequellen verwendet werden [2, 3]. Bei all diesen Anwendungen ist der Schlüsselparameter die Information über die Menge der akkumulierten Energie im Superkondensator [4, 5]. Leider ist die bekannte Beziehung für typische Kondensatoren, die es ermöglicht, die Informationen zu bestimmen, d. h. (1/2)C U ² , kann nicht verwendet werden [6]. Die Menge der akkumulierten Energie kann nicht allein anhand der Spannung an den Kondensatorklemmen bestimmt werden. Der Hauptgrund hierfür ist der mit der Ladungsumverteilung verbundene Diffusionsprozess [1, 7]. Aus diesem Grund haben viele Forscher versucht, ein Superkondensatormodell zu entwickeln, das es ermöglicht, das Verhalten eines realen Systems abzuschätzen. Derzeit verwenden Forscher hauptsächlich die Kombinationen typischer elektronischer Elemente, z. B. RC vierpolige oder Reihen- und Parallelkombinationen solcher Elemente. Alle diese Modelle gehen jedoch von einer Beziehung zwischen Superkondensatorstrom und -spannung an seinem Anschluss in Form einer typischen Differentialgleichung ganzer Ordnung aus [3–5, 7].

Es stellt sich jedoch heraus, dass durch die Anwendung der Bruchrechnung [8, 9] einige völlig neue Möglichkeiten der Energieabschätzung in solchen Systemen erreicht werden können. Die Differenzintegralrechnung nicht ganzzahliger Ordnung wurde vor über 300 Jahren vorgeschlagen, aber wichtige Implementierungsprobleme hängen mit dem Aufkommen von Computern und ihrer Verwendung bei der Modellierung zeitdiskreter dynamischer Systeme zusammen [10–14]. Die Anwendung der Bruchrechnung auf das Problem der Parameterschätzung von Superkondensatoren ist kein neues Thema. Auf diesem Gebiet gibt es viele Veröffentlichungen [15–25]. Die Autoren haben die Aufgabe, Parameter sowohl im Frequenz- als auch im Zeitbereich zu schätzen [26].

Dieses Papier ist eine erweiterte Version der Konferenzpräsentation des Autors [27], in der ein Ansatz mit gebrochener Ordnung kurz vorgestellt wurde, um die im Superkondensator akkumulierte Energie abzuschätzen.

Eine genaue Schätzung der Parameter der Superkondensatoren ist auch für die Beurteilung ihrer Zuverlässigkeit von größter Bedeutung [28–31]. Permanente Degradationsprozesse innerhalb des Superkondensators können den äquivalenten Serienwiderstand und die Kapazität verändern. Somit ermöglicht eine genaue Bestimmung dieser Parameter basierend auf der vorgeschlagenen Methode auch eine genaue Bewertung der Leistung des Kondensators.

Dieses Papier beginnt mit einigen Vorbemerkungen im Zusammenhang mit der Integration und Differenzierung nach gebrochener Ordnung. Als nächstes stellt es die Parameterschätzungsmethode vor, die während der Tests verwendet wurde, und schlägt eine neue Energieberechnungsmethode basierend auf der Bruchrechnung vor. Der Abschnitt Ergebnisse und Diskussion stellt die berechnete Energie für verschiedene Szenarien dar und vergleicht sie mit Referenzwerten (gemessenen Werten). Schlussfolgerungen und Beiträge sind im Abschnitt Schlussfolgerungen zusammengefasst.

Methoden

Die Verwendung poröser Materialien in Superkondensatoren und die spezielle Art der Ladungsakkumulation führen dazu, dass die traditionellen Ansätze, die auf Ableitungsmodellen ganzer Ordnung basieren, nicht genau genug sind. Viele Forscher haben verschiedene Lösungen in Form einer Kombination von typischen RC . vorgeschlagen Elemente mit konstanten oder variablen Werten [4, 7]. Es stellt sich jedoch heraus, dass mit Differentialrechnungen nicht ganzzahliger Ordnung zur Definition der Beziehungen zwischen Strom und Spannung des Superkondensators eine deutlich bessere Genauigkeit erzielt werden kann [17, 19]. Darüber hinaus kann eine solche Lösung zu einer sehr einfachen Modellstruktur führen, während sie eine sehr hohe Genauigkeit bietet [18].

Bruchordnungsdifferenz–Integralrechnung

Die Differentialrechnung nach gebrochener Ordnung ist seit über 300 Jahren bekannt. Allerdings hat es erst in den letzten Jahren seine Popularität bei der Modellierung physikalischer Phänomene und Prozesse gebracht. Es wird angenommen, dass die Beschreibung der Dynamik mit einer Ableitung oder einem Integral nicht ganzzahliger Ordnung eine der effektivsten Methoden zur Modellierung realer Eigenschaften vieler komplexer Phänomene und industrieller Prozesse sein kann, insbesondere basierend auf neuartigen Materialien und Technologien [10, 12, 13 , 32–34].

Differential- oder Integralrechnung nicht ganzzahliger Ordnung ist eine Verallgemeinerung der klassischen Analysis auf die Ordnung α das gehört zur Menge der reellen Zahlen \(\mathcal{R}\). Der Differo–Integraloperator der Ordnung \(\alpha\in\mathcal{R}\) der Funktion f (t ) auf der Strecke [a ,t ] kann wie folgt geschrieben werden

unter der Annahme, dass die Funktion f (t ) ist mehrfach differenzierbar und integrierbar. Für den Operator (1) gibt es viele Definitionen seiner Realisierung. Solche Definitionen unterscheiden sich in Eigenschaften und Anwendungsgebieten. Am bekanntesten sind die Riemann-Liouville-, Caputo- und Grünwald-Letnikov (GL)-Definitionen [34]. Letzteres wird in dieser Arbeit in der Form

wobei das Binomial \(\alpha \choose j\) wie folgt definiert ist

Um ein Bruchmodell zu diskreten Zeitpunkten zu erhalten, wird die GL-Definition in diskreter Form vereinfacht als

Es gibt mehrere Diskretisierungsschemata für die GL Gl. (4). Zu den beliebtesten zählen Rückwärtsdifferenzen (Euler), Trapez (Tustin) und Al Alaoui-Operatoren. Unter Verwendung des Euler-Verfahrens wird die fraktionale Ableitung zu diskreten Zeitpunkten k kann als

Die unendliche Summe der vorherigen Abtastwerte muss in realen Systemen aufgrund des begrenzten Speichers und der begrenzten Rechenzeit auf einen endlichen Wert begrenzt werden. Nun ist die abgeschnittene oder zeitdiskrete Näherung endlicher Länge von GL

wo f (l )=0 für l <0 und L ist die Länge des Modells (6) [23]. Eine Verringerung der Anzahl der Abtastwerte führt zu einer verringerten Berechnungsgenauigkeit. Dies ist wichtig für Systeme, die in einer kontinuierlichen Zeit arbeiten. Einige andere Arten von Lösungen sind Algorithmen, die fraktionale Differo-Integrale mit Modellen ganzer Ordnung approximieren. Ein Beispiel hierfür sind die rekursiven Filter von Oustaloup [35]. Ein weiteres effektives Modell mit endlicher Länge ist die FFLD, eine Kombination aus dem verkürzten Modell (6) und einer Laguarre-basierten Differenz [24, 36, 37].

Alle Ergebnisse der Identifizierung sowie der Energiemessungen werden basierend auf allen Proben im (langen) Beobachtungsfenster L . gewonnen , d. h. mit höchster Genauigkeit. Abbildung 1 zeigt die nach (6) erhaltenen Sprungantworten der Integration und Differentiation für k =0,1,…,L und für verschiedene Werte der Integrations-/Differenzierungsordnung α . Angenommen verschiedene Werte der Ordnung α , kann man verschiedene physikalische Prozesse genauer modellieren, insbesondere Diffusionsprozesse.

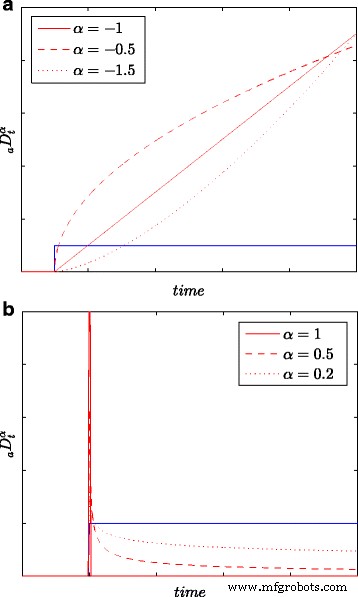
Sprungantworten zum Integrieren (a ) und Differenzierung (b ) Modelle mit verschiedenen Ordnungen α

Parameterschätzung für Bruchmodell

Die Ergebnisse aller in diesem Papier vorgestellten Energiemessungen und Identifizierungsverfahren wurden für einen Superkondensator erhalten, der von einer kontrollierten Spannungsquelle geladen wurde. In einem solchen System beträgt der Superkondensatorstrom i _C (t ) muss durch einen Widerstand R . begrenzt werden in Reihe mit dem Superkondensator C . geschaltet (Abb. 2). Die Schätzung aller Superkondensatorparameter erfolgt basierend auf der Quadripolantwort u _C (t ) zur Spannungsstufe u (t ) an seinem Eingang. Auswahl des geeigneten Werts der Ableitungsordnung α ermöglicht die Berücksichtigung eines Superkondensatormodells der physikalischen Phänomene im Zusammenhang mit Diffusionsprozessen, die mit der Ladungsumverteilung während der Lade- und Entladeprozesse verbunden sind. Der Parallelwiderstand r _P ermöglicht zusätzlich die Modellierung des Ableitstroms. Unter Verwendung der fraktionalen Differentialrechnung zum Modellieren von Superkondensatoren kann die Modellstruktur von geringer Komplexität sein. Für Superkondensatoren, die von der Spannungsquelle geladen werden, besteht ein Modell nur aus zwei Elementen, d. h. einem einfachen RC Vierpol (Abb. 2a). Bei kleinen Kapazitäten beträgt der Serienwiderstand r _S von Bedeutung ist (Abb. 2b), während der Ableitstrom I _L kann zusätzlich durch den Parallelwiderstand r . dargestellt werden _P (Abb. 2c). Unter Verwendung der Berechnung gebrochener Ordnung zum Modellieren des Superkondensators kann die Beziehung zwischen der Spannung an den Kondensatoranschlüssen und seinem Strom wie folgt ausgedrückt werden

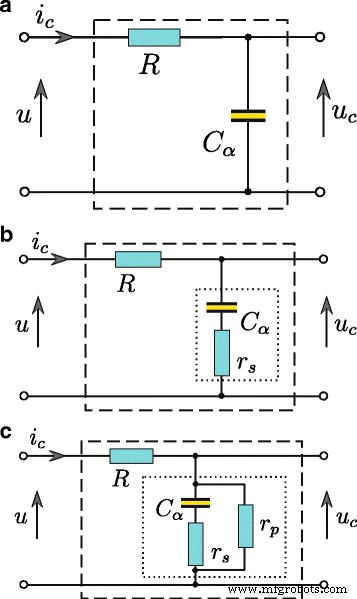
Superkondensator RC Modelle, Basismodell (a ), erweitert mit einem Serienwiderstand (b ) und mit zusätzlichem Parallelwiderstand (c )

wobei der Operator d ^α /dt ^α bedeutet einen Differenzierungsoperator der Ordnung α und die SI-Einheit von C _α ist [F/sec ^1−α ]. Die in Abb. 2a dargestellte grundlegende Superkondensatorkonfiguration kann als Trägheitssystem erster Ordnung behandelt und durch die Bruchübertragungsfunktion

wo T =R C _α . Berücksichtigung des Serienwiderstandes r _S (Abb. 2b) wird die Schaltung als phasenverzögertes Korrektursystem mit der Übertragungsfunktion behandelt (vgl. [24])

wo T ₁ =C _α (R +r _S ) und T ₂ =r _S C _α . Unter Berücksichtigung des Parallelwiderstands r _P repräsentiert den Leckstrom I _L (Abb. 2c) kann die Systemübertragungsfunktion ausgedrückt werden als

wo K =R /r _P +1, T ₁ =C (R r _s /r _P +R +r _S ) und T ₂ =r _S C . Im Zeitbereich gilt Gl. (10) kann als

Das Zeitverhalten des durch (11) definierten Modells wurde erhalten, indem es in die in Abb. 3 grafisch dargestellte Form transformiert wurde, wobei Integrations- und Differenzierungsoperationen von gebrochener Ordnung α . sind . Dieses Modell wurde während des Prozesses der Schätzung der Superkondensatorparameter verwendet. Der getestete Superkondensator wurde unter Verwendung des in Fig. 4a dargestellten Systems identifiziert. Das Steuerungsverfahren des Gesamtsystems wurde mit der Software Matlab/Simulink mit xPC Toolbox entwickelt. Das System bestand aus einem Desktop-PC (xPC Target) mit der installierten Messkarte NI-DAQ und einem Leitrechner (xPC Host). Die Computer waren über das Ethernet-Netzwerk miteinander verbunden. Das Laden und Entladen des Superkondensators erfolgte durch eine (spannungsgesteuerte) Spannungsquelle (Abb. 4b) mit einer Stromausbeute bis ± 3 A. Das Messsystem wurde mit der Abtastfrequenz von 100 Hz betrieben, während alle Messungen und analogen Steuersignale mit 16-Bit-Auflösung verarbeitet [25].

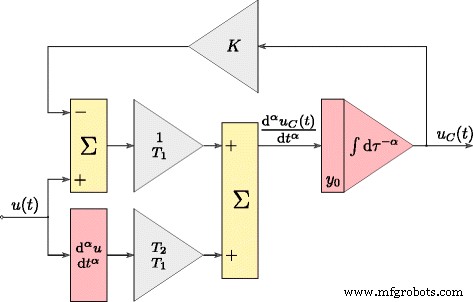
Matlab-Struktur des Superkondensatormodells im Zeitbereich

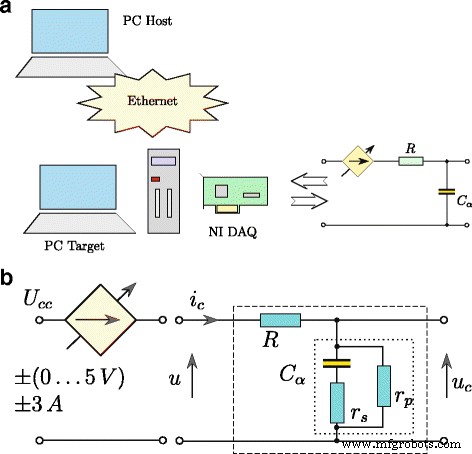
Aufbau des Messsystems (a ) und Superkondensator-Lade-/Entladeschema (b )

Die Hauptmethode zur Bestimmung der dynamischen Eigenschaften eines Systems basiert auf der Analyse der Sprungantwort [38]. In Bezug auf das Systemmodell ermöglicht dieses Verfahren die Schätzung seiner Parameter. Für diese Studie wurde das Sprungsignal mit verschiedenen Spannungen (0,5/1,0/1,5/2,0/2,7 V) und konstanter Dauer (500 s) verwendet (siehe Abb. 5 und Tabelle 2). Andererseits ist eine der typischen Anwendungen von Superkondensatoren die Akkumulation oder Abgabe von Energie in die Stromversorgungssysteme. In diesem Fall ist die Spannungsänderungsrate eher gering. Zur Simulation wurde das 400 mVpp und 0,03 rad/s Signal mit 2 V Offset verwendet (Abb. 6). Um zusätzlich den Einfluss der Spannungs- und Frequenzänderungen auf die geschätzten Parameter zu untersuchen, wurden verschiedene Werte der letzteren verwendet (siehe Tabelle 3).

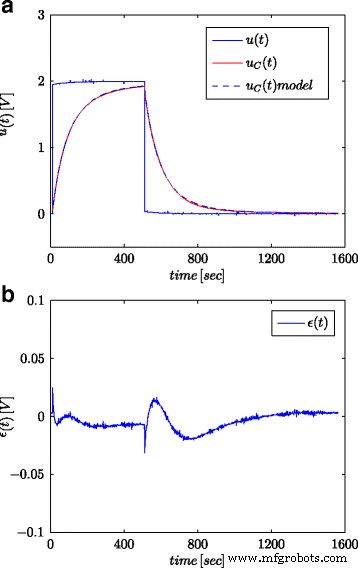
Sprungantworten für getesteten Superkondensator und sein Bruchmodell (a ) und der Modellantwortfehler (b )

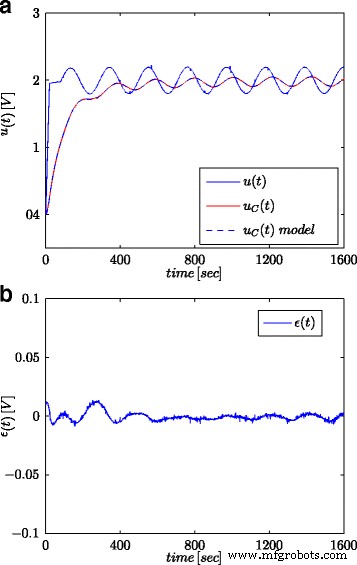
Sinuswellenantworten für getesteten Superkondensator und sein Bruchmodell (a ) und der Modellantwortfehler (b )

Es gibt verschiedene Methoden zur Schätzung von Modellparametern. Das Hauptziel des in dieser Arbeit angewandten Identifizierungsverfahrens im Zeitbereich war die Schätzung des Vektors unbekannter Parameter θ =[α ,C _α ,r _S ,r _P ] des Bruchmodells, das von (11) präsentiert wird. Die Methode der kleinsten Quadrate wurde verwendet, um den Anfangsfehler zu minimieren. Ein Optimierungskriterium beinhaltete die Minimierung des Standardfehlers \(\|\epsilon (k)\|_{2}^{2}\), wobei

wo du _C (k ) ist die gemessene Ausgangsspannung des getesteten Systems im Moment k , während \(\hat{u}_{C}(k)\) die Ausgangsspannung aus dem betrachteten Modell für das Eingangssignal u . ist (k ). Das Identifikationsproblem wird nun darauf reduziert, einen Parametervektor θ . zu finden Θ _Anzeige das würde das Quadratkriterium J minimieren so, dass

wo Θ _Anzeige bezeichnet die Menge der zulässigen Parameterwerte und N bedeutet die Simulationszeit. Es gibt viele Optimierungsalgorithmen, die verwendet werden können, um das Problem zu lösen (13). Die in diesem Papier präsentierten Ergebnisse wurden durch die Implementierung des genetischen Algorithmus in der Matlab-Umgebung erhalten.

Energieberechnung

Eine Änderung der im Superkondensator gespeicherten Energie hängt von der dem Kondensator pro Zeiteinheit zugeführten Leistung ab und kann wie folgt beschrieben werden

Indem die dem Kondensator zugeführte Leistung als Produkt aus Strom und Spannung an den Kondensatorklemmen ausgedrückt wird, ergibt sich die Energieänderung zu einem gegebenen Zeitpunkt t kann ausgedrückt werden als

Die Gesamtenergie während des Zeitintervalls [t ₁ ,t ₂ ] kann durch Integration der Energieänderungen über diese Zeit erhalten werden

Bilanzierung von Gl. (7) kann der Gesamtenergiespeicher bestimmt werden als

Angenommen t ₁ =0 und \(E_{t_{1}}=0\), die im Superkondensator während des Zeitintervalls [0,t . gespeicherte Gesamtenergie ] ist

Beachten Sie, dass für α =1 Gl. (18) kann auf das klassische reduziert werden

Ergebnisse und Diskussion

Zunächst wurde das Verfahren zum Schätzen des Parametervektors des Superkondensatormodells unter Verwendung der Bruchrechnung durchgeführt. Die Schätzung wurde basierend auf dem in Fig. 2c dargestellten System durchgeführt, das an seinem Eingang einen Spannungssprung oder eine Sinuswelle erzeugte. Die Modellantworten wurden basierend auf (11) berechnet. Die Ergebnisse der beiden Identifizierungsverfahren sind sehr ähnlich, insbesondere im Fall der Bruchkapazität C _α und die gebrochene Ordnung α (siehe Tabelle 1). Einige Unterschiede in den Schätzungen des Serienwiderstands r _S kann eine Folge der Frequenzabhängigkeit sein. Das Stufensignal besteht aus vielen hochfrequenten Harmonischen, während die Sinuswelle nur eine – die 0,03 rad/s – umfasst. Die präsentierten Ergebnisse wurden für den kommerziellen Superkondensator Samwha Green-Cap EDLC(DB) mit einer Nennspannung von 2,7 V mit einer Nennkapazität von 100 F und 8 mΩ . erhalten maximaler äquivalenter Serienwiderstand (r _S ) bei 1 kHz.

Fig. 5a und 6a zeigen die gemessene Superkondensatorspannung und die berechneten Modellantworten für stufenförmige bzw. sinusförmige Signale, während 5b und 6b zeigen den Modellantwortfehler.

Alle erhaltenen Ergebnisse zeigen eine hohe Konsistenz zwischen Modellantworten und realen Messungen, obwohl relativ einfache Modelle vorgeschlagen wurden. Einige Diskrepanzen können aus der Tatsache resultieren, dass Modellparameter im System von Superkondensatoren, die mit der Stromquelle geladen und entladen werden, geschätzt werden sollten [25]. Auch sehr hohe Schätzungen von r _P könnte vermuten, dass dieser Widerstand aus dem Superkondensatormodell in Abb. 2c ausgeschlossen werden könnte. Diese sehr hohen Schätzungen und ihre hohen Diskrepanzen für verschiedene Eingaben weisen darauf hin, dass die zum Schätzen dieses Parameters verwendeten Testsignale nicht richtig sind. Als allgemeinste Form wurde das Modell (10) verwendet. Um jedoch alle seine Parameter genau zu bestimmen, mussten andere Verfahren und Testsignale verwendet werden. Der Wert von r _P charakterisiert den Ableitstrom I _L und sollte mit dem konstanten Spannungssignal bestimmt werden, aber für eine sehr lange Zeit – in der Größenordnung von mehreren Dutzend Stunden.

Obwohl das Hauptziel der Studie darin bestand, Energie zu messen, beeinflussten verschiedene Anregungsbedingungen weitgehend alle Parameterschätzungen (siehe Tabelle 2). Zum Beispiel hat die Zunahme der Spannungsstufenamplitude die fraktionale Integrationsordnung als Ergebnis der zunehmenden Wirkung der Diffusionsphänomene innerhalb des Superkondensators signifikant verändert. Aus Tabelle 2 ist auch ersichtlich, dass der Superkondensator ziemlich nichtlinear ist. Als Ergebnis der Änderungen der Integrationsordnung wird auch die Variation der Bruchkapazität beobachtet. Dies gilt auch für sinusförmige Erregung. Die Werte der geschätzten Parameter – insbesondere α und C _α —abhängig von Amplitude und Frequenz (siehe Tabelle 3). Für niedrige Frequenzen ist der Amplitudenwert wichtig, während sich der Superkondensator für höhere Frequenzen verhält, als würde er mit einer konstanten Spannung angeregt.

Energieberechnung

Fig. 7a und 8a zeigen gemessene Werte der Spannung und des Stroms des Superkondensators für die Konfiguration, wie sie in Fig. 4b dargestellt ist. Diese Werte wurden zur Berechnung der im Kondensator gespeicherten Gesamtenergie verwendet (gekennzeichnet als E ₁ in Abb. 7b und 8b) nach (16). Ebenso wie bei Parameteridentifikationsverfahren wurden die Berechnungen sowohl für den Spannungssprung als auch für die Sinuswelle am Systemeingang durchgeführt. Die so berechnete Energie für jede Zeit t wurde mit Energie verglichen, die auf der Grundlage der Spannung und Kapazität gemäß (19) berechnet wurde (gekennzeichnet als E ₃ in Abb. 7b und 8b) und Energie berechnet mit Bruchrechnung (gekennzeichnet als E ₂ in Abb. 7b und 8b) nach (18). Für Gl. (19) wurde ein Nennwert des Superkondensators angenommen (C _n ), während in (18) der Wert aus dem in Tabelle 1 dargestellten Schätzverfahren verwendet wurde. Abbildung 7b zeigt Ergebnisse von Messungen und Energieberechnungen für den Spannungssprung, während Abbildung 8b dieselben Größen für die Sinuswelle zeigt. Ähnliche Berechnungen wurden für verschiedene Spannungsstufen und sinusförmige Anregungen durchgeführt. Abbildung 9a, b zeigt ein Beispiel für gemessene und berechnete Energien für zwei Spannungsstufen von 0,5 V bzw. 2,7 V. Abbildung 10 zeigt die Energieänderungen für ein sinusförmiges Signal mit der Frequenz 0,03 rad/sec und unterschiedlichen Amplituden von 0,1/0,25/0,5 und 0,7 V. Es ist zu erkennen, dass die Unterschiede in den ermittelten Energiewerten Unterschieden in den Schätzwerten entsprechen der gebrochenen Ordnung α . Je größer die Differenz vom Wert − 1 ist, desto größer ist die Differenz der berechneten Energien.

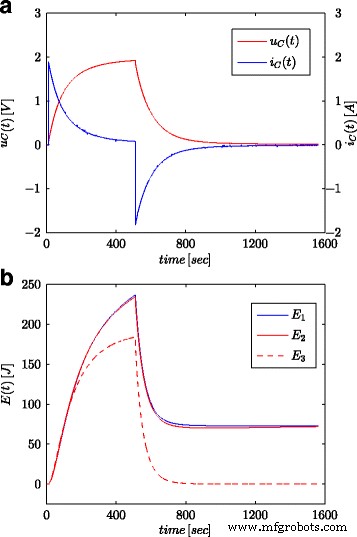
Sprungantworten für Superkondensatorspannung und -strom (a ) und berechnete Energiewerte (b )

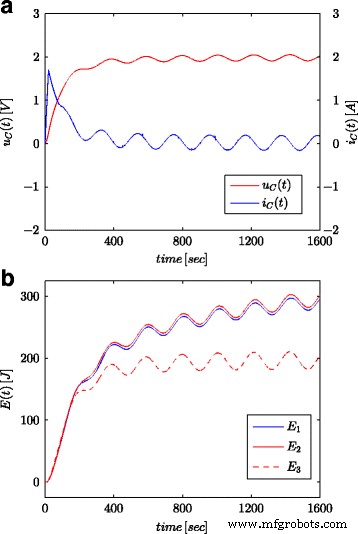
Sinusförmiges Verhalten für Superkondensatorspannung und -strom (a ) und berechnete Energiewerte (b )

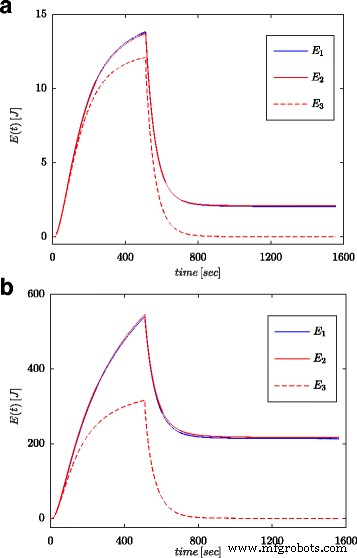
Berechnete Energiemengen für Stufenanregungen von 0,5 V (a ) und 2,7 V (b )

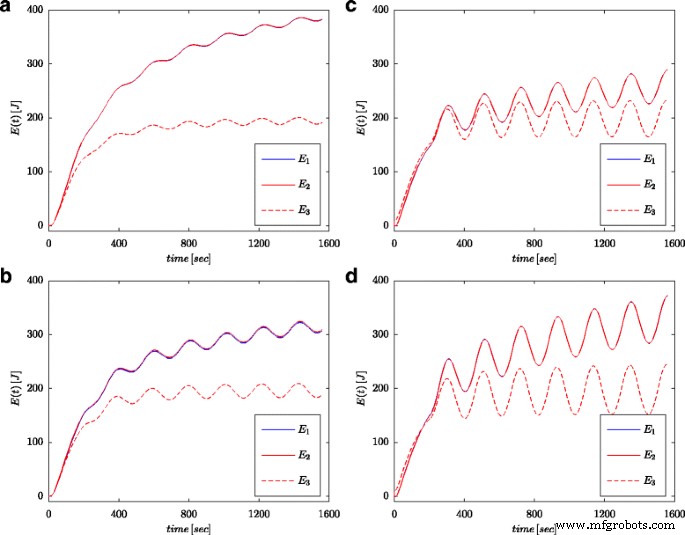
Berechnete Energiemengen für sinusförmige Anregungen mit Frequenz 0,03 rad/s und Amplituden 0,1 V (a ), 0,25 V (b ), 0,5 V (c ) und 0,7 V (d )

Diskussion

Die Verwendung von Elektroden aus porösem Material in Superkondensatoren in Form von Aktivkohle, die durch einen sehr dünnen Separator isoliert sind, und die Verwendung von Ladungsakkumulationsmechanismen als sogenannte Doppelschicht führt zu einer enormen Erhöhung ihrer Kapazität. Die Anwendung neuer Materialien und neuer Designlösungen führt jedoch dazu, dass traditionelle mathematische Berechnungen in Form von Ableitungen und Integralen ganzzahliger Ordnung ungenau erscheinen. Die durchgeführten Messungen und Berechnungen belegen die Natur von Superkondensatoren mit gebrochener Ordnung. Durch korrekte Schätzung der nicht ganzzahligen Ordnung α Ableitung/Integral kann man Phänomene und Prozesse, die innerhalb des Superkondensators auftreten, mit einfachen mathematischen Modellen genau modellieren.

Unter Berücksichtigung des durch (16) bestimmten reellen Wertes der akkumulierten Energie unterschätzt das Modell ganzzahliger Ordnung mit nominalen Parametern (19) die Energiemenge, während das Bruchmodell (18) fast denselben Wert anzeigt.

Die durchgeführten Tests und Messungen bezogen sich auf das Laden und Entladen des Superkondensators durch eine Spannungsquelle. Unter industriellen Bedingungen werden Superkondensatoren normalerweise durch Stromquellen geladen und entladen. Dies kann die Natur des Systems ändern, da der Kondensator kein Trägheitssystem mehr ist, sondern ein typisches integrierendes System wird. Die vom Autor durchgeführten Messungen weisen aber auch auf das Auftreten von Diffusionsprozessen in solchen Fällen hin. Jedenfalls wird hier die Nützlichkeit des Gründwald-Letnikov-Derivats/-Integrals bestätigt. Ein weiteres Problem hängt mit der Implementierung des GL-Differo-Integral-Operators zusammen, z. B. der endlichen oder abgeschnittenen GL-Differenz (6), die rechenaufwändig sein kann. In zukünftigen Untersuchungen werden wir die Approximatoren Oustaloup [35] und FFLD [24, 36, 37] vergleichen, um das Implementierungsproblem effektiv zu lösen.

Die Menge der Energiespeicherung im Superkondensator, die nur anhand des gemessenen Wertes der Superkondensator-Klemmenspannung und unter Verwendung von Modell (19) berechnet wird, ist nicht angemessen. Das Modell (19) ist nur gültig, wenn der Kondensatorstrom durch die ganzzahlige Ableitung der Kondensatorspannung (i _C (t )=du _C (t )/dt ). Für Superkondensatoren gilt dies konstruktionsbedingt und aufgrund der verwendeten Sondermaterialien nicht. Das gleiche Problem tritt jedoch bei sehr großen Superkondensatoren auf, die von einer Stromquelle geladen werden. Es gibt auch ganz neue Elemente wie Super-Batterien. In all diesen Anwendungen sind die Stromänderungen aufgrund der spezifischen Eigenschaften dieser Elemente nicht durch die ganzzahlige Ableitung der Klemmenspannung gekennzeichnet.

Schlussfolgerungen

In diesem Beitrag wurde ein neuer Ansatz zur Schätzung einer in Superkondensatoren akkumulierten Energiemenge vorgestellt. Die Analyse wurde unter Ausnutzung bestimmter einzigartiger Eigenschaften von Modellen gebrochener Ordnung durchgeführt. Es hat sich gezeigt, dass die Anwendung solch ausgeklügelter Modellierung zu sehr genauen Ergebnissen führt, die erhalten werden können, obwohl die Modelle selbst nicht von hoher Komplexität sind. Dies ist auf die natürliche Fähigkeit der Dynamik nicht ganzzahliger Ordnung zurückzuführen, Diffusionsprozesse zu modellieren, genau wie die Ladungsumverteilung in Superkondensatoren. Die Ergebnisse dieses Papiers haben die fraktionale Natur von Superkondensatoren bestätigt.