Metallfreie Halbmetallizität in B-dotierten gh-C3N4-Systemen

Hintergrund

Spintronische Bauelemente nutzen gleichzeitig die Ladungs- und Spinfreiheit von Elektronen und haben aufgrund ihrer möglichen Verwendung in Logik- und Speicherbauelementen zunehmende Aufmerksamkeit auf sich gezogen [1, 2]. Ihre Leistung hängt jedoch stark vom Spinpolarisationsverhältnis der Ströme ab. Es besteht daher ein dringender Bedarf an Materialien, die 100% spinpolarisierte Ströme erzeugen können. Halbmetallische Materialien, die dies auf Fermi-Niveau E können _F , gelten als ideale Materialien für spintronische Bauelemente [3,4,5,6]. Viele halbmetallische Ferromagnete, wie dotierte Manganite [7], Doppelperowskite [8] und Heusler-Verbindungen [9, 10], haben in den letzten Jahren große Aufmerksamkeit auf sich gezogen. Diese halbmetallischen Materialien enthalten jedoch normalerweise Übergangsmetalle (TM) und haben starke Spin-Bahn-Kopplungsstärken, was zu kurzen Spinrelaxationszeiten führt. Es ist daher notwendig, fortschrittliche TM-freie halbmetallische Materialien mit langer Spinrelaxationszeit zu entwickeln.

Zweidimensionale (2D) Atomkristalle mit planaren Oberflächen haben in letzter Zeit aufgrund ihrer möglichen Anwendung in Spintronikvorrichtungen viel Aufmerksamkeit auf sich gezogen [11,12,13,14,15,16,17,18,19,20,21,22 ,23,24]. Graphen und seine verschiedenen 2D-Analoga, wie hexagonales Bornitrid und Kohlenstoffnitrid, haben aufgrund ihrer außergewöhnlichen Eigenschaften, z. B. geringer Dimensionalität und Elektroneneinschluss, großes Potenzial für die Spintronik. Obwohl die meisten dieser Materialien von Natur aus nicht magnetisch sind, gibt es viele Möglichkeiten, wie beispielsweise Dotierung und Dehnung, um den halbmetallischen Ferromagnetismus zu erreichen. Zum Beispiel in B, Al und Cu eingebettetes g-C₃ . auf Trizainbasis N₄ (gt-C₃ N₄ ) wurden als halbmetallisch beschrieben [14]. Das graphenähnliche Kohlenstoffnitrid weist auch unter Zugspannung eine Halbmetallizität auf [17]. Darüber hinaus das auf Heptazin basierende g-C₃ N₄ (gh-C₃ N₄ ) hat viel Aufmerksamkeit erhalten [25,26,27,28,29,30,31,32,33].

Zahlreiche Forschungsarbeiten haben die elektronischen und magnetischen Eigenschaften von gh-C₃ . mit eingebautem Übergangsmetall untersucht N₄ Systeme [11, 28, 30]. Diese in Übergangsmetalle eingebetteten gh-C₃ N₄ Materialien wurden bei erhöhter Temperatur synthetisiert [34,35,36,37,38,39]. Theoretische Arbeiten zeigen, dass die Übergangsmetalle stärker mit gh-C₃ . binden können N₄ als bei Graphen und diese Systeme sind metallisch [30]. Indraniet al. haben die magnetischen Eigenschaften von C-Dope gh-C₃ . systematisch untersucht N₄ Systeme durch Dichtefunktionaltheorie (DFT)-Rechnungen [40]. Sie fanden heraus, dass all diese C-Dope gh-C₃ N₄ Systeme sind Ferromagnetismus, und eine hochenergetische Phase zeigt eine starke Halbmetallizität und eine Curie-Temperatur von 400 K. Vor kurzem haben Gao et al. [41] haben experimentell die Fähigkeit demonstriert, das B-dotierte gh-C₃ . herzustellen N₄ Nanoblätter, die Hochtemperatur-Ferromagnetismus und Halbmetallizität aufweisen. Trotz dieser frühen Arbeiten ist eine systematische theoretische Untersuchung des B-dotierten gh-C₃ N₄ wird vermisst. Einige grundlegende Fragen wie die Auswirkungen der Dotierungsposition und der B-Konzentration auf die elektronischen und magnetischen Eigenschaften von gh-C₃ N₄ auf Klärung warten. Darüber hinaus müssen auch die Auswirkungen von Belastungen untersucht werden.

In dieser Arbeit untersuchen wir systematisch die Auswirkungen von Dotierungspositionen, B-Konzentrationen und Dehnungen auf die elektronischen und magnetischen Eigenschaften des B-dotierten gh-C₃ N₄ System durch First-Principles-Berechnungen. Die Ergebnisse zeigen, dass im Grundzustand von B-dotiertem gh-C₃ . eine starke Halbmetallizität gefunden werden kann N₄ (B_C1 @gh-C₃ N₄ ). Nicht nur Dotierungspositionen, sondern auch Dotierungskonzentrationen spielen eine wichtige Rolle beim Induzieren von Halbmetallizität. Darüber hinaus ist die Halbmetallizität in B_C1 @gh-C₃ N₄ kann bis zu 5 % Druckspannung und 1,5 % Zugspannung aushalten. Das B-dotierte gh-C₃ N₄ Systeme sind daher vielversprechend für die Spintronik.

Berechnungsmethoden

Eine tetragonale 28 a.u. Zelle mit zwei primitiven Zellen von gh-C₃ N₄ wie in Fig. 1 gezeigt, wurde verwendet, um das B-dotierte gh-C₃ . zu simulieren N₄ System. Die geometrische Strukturrelaxation und die statische elektronische Strukturberechnung werden unter Verwendung des VASP-Pakets [42, 43] durchgeführt, das auf der Dichtefunktionaltheorie (DFT) basiert. Es werden die generalisierte Gradienten-Approximation (GGA) der Perdew-Burke-Ernzerhof (PBE) [44] und die Projektor-Augmented-Wave-(PAW)-Potentiale verwendet. Die Grenzenergie wird auf 500 eV eingestellt und ein 1 × 9 × 15 Monkhorst-Pack-k-Punkte-Raster wird gewählt, um ein Gleichgewicht zwischen Rechenzeit und Genauigkeit zu erreichen. Alle Geometriestrukturen sind vollständig entspannt. Der Konvergenzschwellenwert ist auf 10 ^–6 . eingestellt eV in elektronischen Schritten und 5 × 10 ⁻³ eV/Å in Kraft. Um die Wechselwirkung zwischen zwei benachbarten periodischen Bildern zu vermeiden, wird der Vakuumbereich entlang des x -Richtung ist auf 15 Å eingestellt. Um die Auswirkungen von Dotierungskonzentrationen zu untersuchen, wird eine tetragonale 112-atomige Superzelle bestehend aus 2 × 2 × 1 tetragonalen Elementarzellen und einem 1 × 5 × 9 Monkhorst-Pack k-Punkte-Gitter verwendet.

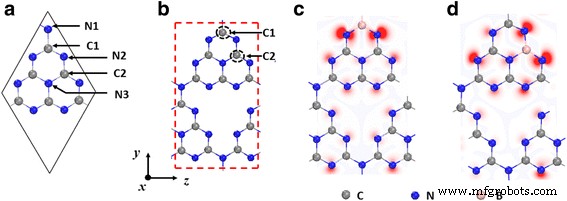
a Schematische Darstellung des makellosen gh-C₃ N₄ . Es gibt zwei unäquivalente C-Atome (C1 und C2) und drei unäquivalente N-Atome (N1, N2 und N3). b Die tetragonale 28 a.u. Zelle von gh-C₃ N₄ wird hier verwendet, um das B-dotierte gh-C₃ . zu simulieren N₄ (entsprechend 8,33 % Dotierungskonzentration). Die schwarzen gestrichelten Kreise zeigen die möglichen B-Dotierungsstellen an. c , d Die optimierten Strukturen von B_C1 @gh-C₃ N₄ und B_C2 @gh-C₃ N₄ , bzw. Verteilungen der Ladungsdichte des Spin-Up-Zustands minus des Spin-Down-Zustands für B_C1 @gh-C₃ N₄ und B_C2 @gh-C₃ N₄ werden auch hier angezeigt. Die roten und blauen Farben kennzeichnen die Spin-up- bzw. Spin-down-Gebühren

Ergebnisse und Diskussionen

In einem reinen gh-C₃ N₄ System gibt es zwei inäquivalente C-Atome (C1 und C2) und drei inäquivalente N-Atome (N1, N2 und N3), wie in Abb. 1a gezeigt. Wir finden die relaxierten Gitterparameter (a = b = 7.14 Å) des reinen gh-C₃ N₄ stimmen gut mit früheren experimentellen und theoretischen Berichten überein [40, 45]. Die Bandstruktur und die entsprechende Gesamtzustandsdichte (DOSs) von gh-C₃ N₄ sind in Abb. 2a dargestellt. Um die elektronischen Eigenschaften des gh-C₃ besser zu verstehen N₄ , die Ladungsverteilungen der Kantenbänder C ₁ , V ₁ , und die entsprechende lokale Zustandsdichte sind in Abb. 2b, c dargestellt. Es ist deutlich zu erkennen, dass die Unterseite des Leitungsbandes C ₁ wird dominiert von π ^* Zustände von C1-, C2- und N3-Atomen, die aus dem p _x Orbitale. Die Spitze des Valenzbandes V ₁ wird durch die nichtbindenden δ-Zustände von N2-Atomen und die π-Zustände von N3-Atomen bestimmt.

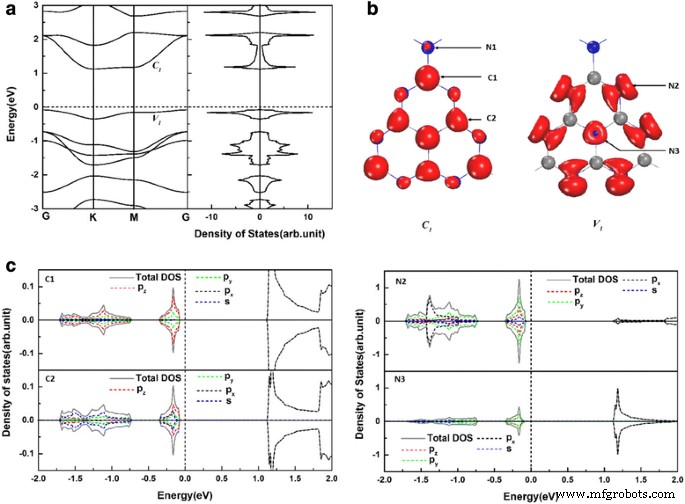
a Die elektronischen Bandstrukturen und die Gesamtzustandsdichte von unberührtem gh-C₃ N₄ . b Die Ladungsverteilungen der Kantenbänder C ₁ und V ₁ (indiziert in a ). c Die orbitalaufgelöste Elektronendichte von Zuständen projiziert auf C1-Atom, C2-Atom, N2-Atom und N3-Atom (indiziert in b ). Die Energie auf dem Fermi-Niveau wird auf Null gesetzt

Eine tetragonale Elementarzelle mit 28 Atomen gh-C₃ N₄ (entsprechend 8,333% Dotierungskonzentration) wird verwendet, um das B-dotierte gh-C₃ . zu simulieren N₄ wie in Abb. 1b (die rote gestrichelte Linie) gezeigt. Nach Berücksichtigung früher Berichte [31], dass die Substitution an den C-Zentren (C1 und C2) günstiger ist als an den N-Zentren (N1, N2 und N3), wurden nur die Konfigurationen von B, die C substituiert haben, untersucht, um ihre magnetischen Eigenschaften. Als Ergebnis werden die beiden unterschiedlichen B-dotierten gh-C₃ N₄ Isomere (B_C1 @gh-C₃ N₄ und B_C2 @gh-C₃ N₄ ) studiert. Die vollständig relaxierten Strukturen von B_C1 @gh-C₃ N₄ und B_C2 @gh-C₃ N₄ sind in Abb. 1c bzw. d angegeben.

Die strukturelle Stabilität hängt vom Ausmaß der Kohäsion ab und das System mit negativer und großer absoluter Kohäsionsenergie hat eine bessere Stabilität. Die kohäsiven Energien (E _coh ) von B_C1 @gh-C₃ N₄ und B_C2 @gh-C₃ N₄ wurden berechnet mit

wo E _tot ist die Gesamtenergie eines B-dotierten gh-C₃ N₄ System und E _ich ist die Energie eines isolierten Atoms für das Element i in derselben Zelle. Die M _ich und M sind die Nummern der i Spezies und die Gesamtzahl der Atome im B-dotierten gh-C₃ N₄ System bzw. Wir finden, dass die Kohäsionsenergien − 6.107 und − 6.097 eV pro Atom für B_C1 . betragen @gh-C₃ N₄ und B_C2 @gh-C₃ N₄ , bzw. Somit ist der B_C1 @gh-C₃ N₄ Phase ist energetisch günstig. Diese Schlussfolgerung stimmt gut mit der vorherigen Arbeit überein [31]. Um die relative Stabilität der beiden B-dotierten gh-C₃ . weiter zu untersuchen N₄ Systeme, die Kohäsionsenergien von 2D C₂ N und gh-C₃ N₄ , die experimentell synthetisiert wurden, berechnet und entsprechen − 6.813 bzw. − 6.091 eV pro Atom. Interessanterweise sind sowohl B_C1 @gh-C₃ N₄ und B_C2 @ gh-C₃ N₄ haben mittlere Kohäsionsenergien zwischen C₂ N und gh-C₃ N₄ . Folglich sollten sie eine mittlere strukturelle und mechanische Stabilität aufweisen.

Um die thermodynamische Machbarkeit und die relativen Energiekosten von B_C1 . zu bestimmen @gh-C₃ N₄ und B_C2 @gh-C₃ N₄ im Vergleich zu ihren makellosen 2D-Analoga wurden die Bildungsenergien auch mit

wo E _tot , M _ich , und M sind die gleichen wie bei der Berechnung der Kohäsionsenergie. μ _ich ist das chemische Potential des i te Art. Hier werden Graphen, rhomboedrisches Bor und gasförmiger Stickstoff verwendet, um die chemischen Potentiale μ . zu bestimmen _C , μ _B , und μ _N , bzw. Die berechneten Bildungsenergien betragen 0,222 und 0,232 eV pro Atom für B_C1 . @gh-C₃ N₄ und B_C2 @gh-C₃ N₄ , bzw. Zum Vergleich:Die Bildungsenergie von gh-C₃ N₄ beträgt 0,293 eV pro Atom. Außerdem ist das berechnete E _f Werte von B_C1 @gh-C₃ N₄ und B_C2 @gh-C₃ N₄ sind etwas niedriger als gh-C₃ N₄ , was auf diese B-dotierten gh-C₃ hinweist N₄ Isomere hergestellt werden können. Tatsächlich ist die Synthese von B-dotiertem gh-C₃ N₄ wurde berichtet [41].

Um die magnetischen Grundzustände von B_C1 . herauszufinden @gh-C₃ N₄ und B_C2 @gh-C₃ N₄ , haben wir die nicht-Spin-polarisierten (NSP), ferromagnetischen (FM) und antiferromagnetischen (AFM) Zustände untersucht. Die Ergebnisse zeigen, dass der FM-Zustand der Grundzustand für die beiden B-dotierten gh-C₃ . ist N₄ Systeme, und ihre magnetischen Momente sind beide 1,0 μ _B pro Elementarzelle, wie in Tabelle 1 gezeigt. Zum weiteren Verständnis des Magnetismus der beiden B-dotierten gh-C₃ N₄ Systeme, die spinabhängigen Ladungsdichten von B_C1 @gh-C₃ N₄ und B_C2 @gh-C₃ N₄ wurden untersucht und in Abb. 1c bzw. d dargestellt. Etwas anders als das C-dotierte gh-C₃ N₄ Systeme, bei denen die Spindichte hauptsächlich an den dotierten C-Plätzen liegt [40], die Spindichte von B-dotiertem gh-C₃ N₄ ist hauptsächlich an den zweifach koordinierten N2-Atomen lokalisiert, insbesondere an den N2-Atomen, die den Dotierstoff-B-Atomen benachbart sind, wie in Abb. 1c, d gezeigt. Da B-Dotierstoff ein Elektron weniger hat als das substituierte C-Atom, wird in B-dotiertem gh-C₃ . ein π-Defekt induziert N₄ System, was zu 1,0 μ . führt _B magnetisches Moment.

Um die Auswirkungen der B-Dotierung auf den gh-C₃ zu verstehen N₄ Systeme haben wir die Spin-polarisierte Bandstruktur und die Zustandsdichteberechnungen für B_C1 . durchgeführt @gh-C₃ N₄ und B_C2 @gh-C₃ N₄ , wie in Abb. 3a bzw. d gezeigt. Die Ergebnisse zeigen, dass die Asymmetrie zwischen Spin-Up- und Spin-Down-Dichten in B_C1 @gh-C₃ N₄ und B_C2 @gh-C₃ N₄ induziert einen offensichtlichen Magnetismus. Interessanterweise stellen wir, wie in Abb. 3a gezeigt, fest, dass B_C1 @gh-C₃ N₄ Systeme haben eine halbmetallische Eigenschaft, da einer der Spinkanäle metallisch ist, während der andere isolierend ist. Die Diagramme der Bandstruktur und der Gesamtzustandsdichte zeigen, dass die Spinaufspaltung nahe dem Fermi-Niveau auftritt und zwei Spin-Down-Bänder das Fermi-Niveau kreuzen, während die Spin-Up-Bänder eine Bandlücke von 1,23 eV aufweisen. Dies liegt hauptsächlich an den großen Hohlräumen im gh-C₃ N₄ Rahmen, die zur Lokalisierung elektronischer Zustände führen. Die Bandlücke im Spin-up-Kanal von B_C1 @gh-C₃ N₄ ist viel größer als die Lücken (in einem der Spinkanäle) von dotierten Manganiten [7], Doppelperowskiten [8], Heusler-Verbindungen [9, 10] und Graphen-Nanobändern [46]. Die halbmetallische Festigkeit des B_C1 @gh-C₃ N₄ vergleichbar mit dem C-dotierten gh-C₃ N₄ [40]. Ein so starkes halbmetallisches System ist sehr vielversprechend, da der Spin-Flip-Übergang von Ladungsträgern aus der thermischen Anregung nicht möglich ist. Um die Ursprünge der Halbmetallizität in B_C1 . weiter zu erforschen @gh-C₃ N₄ , die Ladungsverteilungen der beiden Spin-Down-Bänder über das Fermi-Niveau sind in Abb. 3b dargestellt. Wir sehen deutlich, dass die Halbmetallizität von B_C1 @gh-C₃ N₄ kommt hauptsächlich von den nichtbindenden δ-Zuständen von N2-Atomen. Die lokale Zustandsdichte (siehe Abb. 3c) zeigt auch, dass die Halbmetallizität von B_C1 @gh-C₃ N₄ stammt hauptsächlich aus dem p _z Bahnen von N2-Atomen zusammen mit einem Teilbeitrag von p _z Bahnen von B- und N1-Atomen. Sie stimmen gut mit den früheren Berichten zu gt-C₄ überein N₃ [2], wobei die N-Orbitale einen wesentlichen Beitrag zur Halbmetallizität leisten. Für den B_C2 @gh-C₃ N₄ , die Bandstruktur- und Gesamtzustandsdichte-Diagramme (Abb. 3a) zeigen auch, dass die Spinaufspaltung nahe dem Fermi-Niveau auftritt. Der Spin-Majoritätszustand hat eine Bandlücke von 1,36 eV. Der Spin-Minoritätszustand weist jedoch eine Bandlücke von 0,016 eV auf. Die Ladungsverteilungen der Kantenbänder und die lokale Zustandsdichte für B_C2 @gh-C₃ N₄ zeigen, dass sowohl die Valenzbandkanten als auch die Leitungsbandkanten von B_C2 @gh-C₃ N₄ werden von den nichtbindenden δ-Zuständen dominiert, die hauptsächlich von den p _y und p _z Orbitale von N2-Atomen. Dies bedeutet, dass die nichtbindenden δ-Zustände von N2-Atomen gespalten werden, wenn ein B-Atom ein C-Atom in gh-C₃ . ersetzt N₄ System und bestimmen seine elektronischen Eigenschaften.

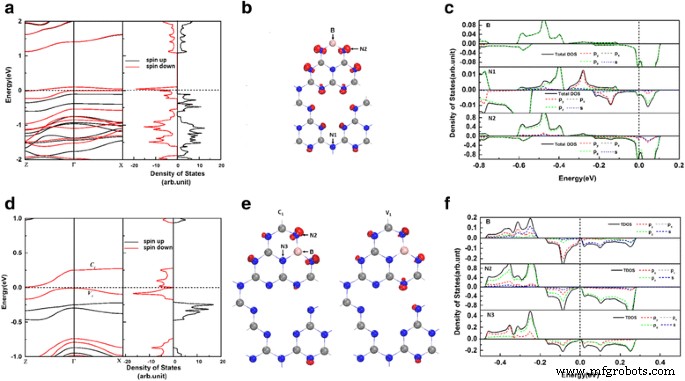
a Die spinabhängige Bandstruktur und die Gesamtzustandsdichte von B_C1 @gh-C₃ N₄ . b Die Ladungsdichten der beiden Bänder, die das Fermi-Niveau kreuzen. c Die orbitalaufgelöste Elektronendichte von Zuständen projiziert auf B-Atom, N1-Atom und N2-Atom (indiziert in b ) für B_C1 @gh-C₃ N₄ . d –f sind gleich mit a –c aber für B_C2 @gh-C₃ N₄ . Die Energie auf dem Fermi-Niveau wird auf Null gesetzt

Um die Abhängigkeit der Halbmetallizität im B_C1 . zu verdeutlichen @gh-C₃ N₄ Systeme auf Dotierungskonzentrationen wurde eine tetragonale 112-atomige Superzelle mit 2 × 2 × 1 tetragonalen Elementarzellen verwendet und drei verschiedene B-Dotierungskonzentrationen (2,083, 4,167 und 6,25 %) untersucht, wie in Abb. 4a, b . gezeigt . Wie wir in Abb. 4b sehen können, ist B_C1 @gh-C₃ N₄ kann die Halbmetallizität bei einer Dotierungskonzentration von 6,25% noch aufrechterhalten. Es verliert jedoch seine Halbmetallizität, wenn die Dotierungskonzentration 4,167% oder weniger beträgt.

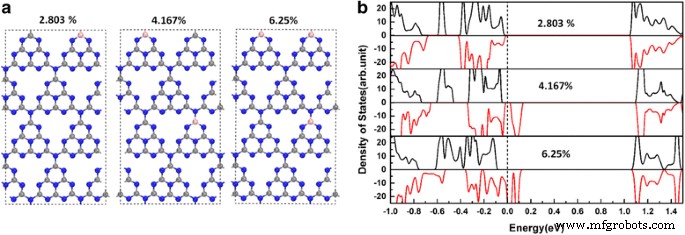
a Schematische Darstellungen der tetragonalen 112-atomigen Superzelle zur Simulation verschiedener Dotierungskonzentrationen von B_C1 @gh-C₃ N_4. b Die spinabhängige Gesamtzustandsdichte von B_C1 @gh-C₃ N₄ mit unterschiedlichen Dotierungskonzentrationen. Die Energie auf dem Fermi-Niveau wird auf Null gesetzt

Die Dehnungstechnologie wird üblicherweise verwendet, um die Spineigenschaften eines magnetischen Materials abzustimmen, und der Dehnungseffekt auf die Halbmetallizität eines Materials sollte untersucht werden. Hier haben wir die Zustandsdichteberechnungen für B_C1 . durchgeführt @gh-C₃ N₄ System unter der in-plain-biaxialen Dehnung. Es hat sich herausgestellt, dass die Halbmetallfestigkeit mit zunehmender biaxialer Zugspannung allmählich abnimmt. Es verliert die Halbmetallizität, wenn die biaxiale Zugspannung 1,5 % erreicht, wie in der Tafel von Abb. 5 gezeigt. Es hält jedoch die Halbmetallizität bis zu 5 % der biaxialen Druckspannung aufrecht (siehe die rechte Tafel von Abb. 5). Somit verhält sich dieses System bei äußerer Belastung gut.

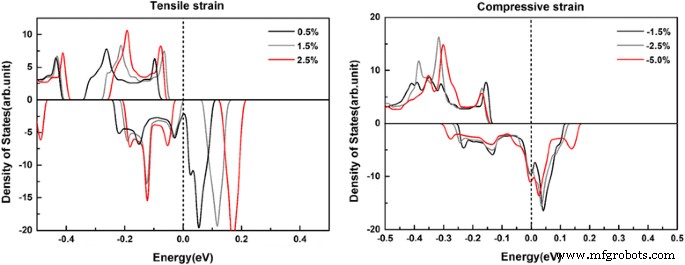
Die spinabhängige Gesamtzustandsdichte von B_C1 @gh-C₃ N₄ (mit 8,33% Dotierungskonzentration) unter in-plain biaxialer Zugbelastung (links) bzw. biaxialer Druckbelastung (rechts). Die Energie auf dem Fermi-Niveau wird auf Null gesetzt

Schlussfolgerung

Basierend auf Berechnungen der Dichtefunktionaltheorie wurde das B-dotierte gh-C₃ N₄ Systeme wurden auf mögliche Anwendungen in spintronischen Geräten untersucht. Ferromagnetismus wird in allen B-dotierten gh-C₃ . beobachtet N₄ Systeme. Außerdem wird eine starke Halbmetallizität nur in der Grundzustandsphase erreicht, d. h. B_C1 @gh-C₃ N₄ , die aus einer Spinaufspaltung der nichtbindenden δ-Zustände hochungesättigter 2-fach koordinierter N2-Atome resultiert. Bei niedrigen B-Dotierungskonzentrationen geht die Halbmetallität verloren. Somit spielen sowohl die selektive Dotierung als auch ihre Konzentration eine wichtige Rolle bei der Induktion von Magnetismus und Halbmetallizität. Die Halbmetallizität in B_C1 @gh-C₃ N₄ kann bis zu 5 % Druckspannung und 1,5 % Zugspannung aushalten. Diese Ergebnisse zeigen, dass das B-dotierte gh-C₃ N₄ Systeme könnten ein ferromagnetisches halbmetallisches Material für Magnetspeicher und Spintronikvorrichtungen sein.