Temperatur- und Druckabhängigkeiten der elastischen Eigenschaften von Tantal-Einkristallen unter <100> Zugbelastung:eine molekulardynamische Studie

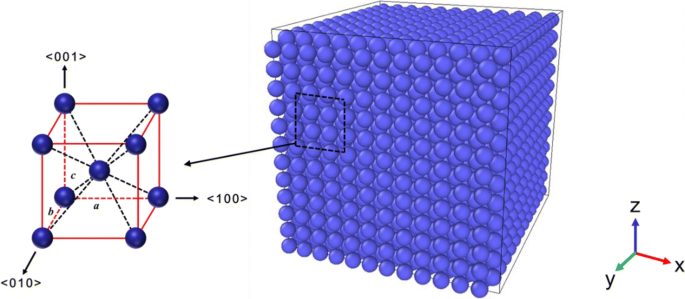
BCC-Struktur und Kartenskizze des kubischen Ta mit einer Kantenlänge von 3,96 nm. Die Kartenskizze ist die ursprüngliche Struktur in unseren aktuellen Simulationen

MD-Simulationsdetails

Unsere MD-Simulationen, über die in diesem Artikel berichtet wird, werden mit dem großskaligen atomaren/molekularen massiv parallelen Simulator (LAMMPS) durchgeführt [19]. Während des Prozesses der MD-Simulation wird die externe Kraft, die auf Ta-Atome ausgeübt wird, gemäß den interatomaren Potentialfunktionen zwischen diesen Atomen berechnet. In dieser Studie werden zwei verschiedene interatomare Potentiale betrachtet:das EAM-Potential von Zhou et al. [20] und Ravelo et al. [21] bzw. Beide Potentiale wurden zur Reproduktion einiger elastischer Eigenschaften von Ta verwendet, die in Tabelle 1 aufgeführt sind. Der Einfachheit halber werden sie als Ravelo-EAM- und Zhou-EAM-Potentiale bezeichnet.

Das elastische Verhalten von Strukturen mit kubischer Symmetrie wird vollständig durch ihre elastischen Konstanten beschrieben, C ₁₁ , C ₁₂ , und C ₄₄ . Der orientierungsabhängige Elastizitätsmodul für <100>-, <110>- und <111>-Einkristalle wird mit den verschiedenen Gleichungen berechnet [18]. In unserer Arbeit werden MD-Simulationen durchgeführt, um die Auswirkungen auf den Elastizitätsmodul unter <100> Zugbelastung zu untersuchen. Daher konzentrieren wir uns auf den Elastizitätsmodul für die <100 >-Orientierung und nehmen den Elastizitätsmodul von E ₁₀₀ berücksichtigen. Folglich betrachten wir die elastischen Konstanten C ₁₁ und C ₁₂ sowie die folgende Gleichung [22]:

Im Allgemeinen gibt es drei Methoden, um die elastischen Konstanten aus MD zu berechnen, einschließlich der Spannungsfluktuationsmethode, der Dehnungsfluktuationsmethode und der direkten Methode. In der vorliegenden Arbeit wird die direkte Methode, die der von Gao et al. [23] wird verwendet, um die elastischen Konstanten C . zu berechnen ₁₁ und C ₁₂ für zwei Arten von EAM-Potentialen, wie in Abb. 2 gezeigt.

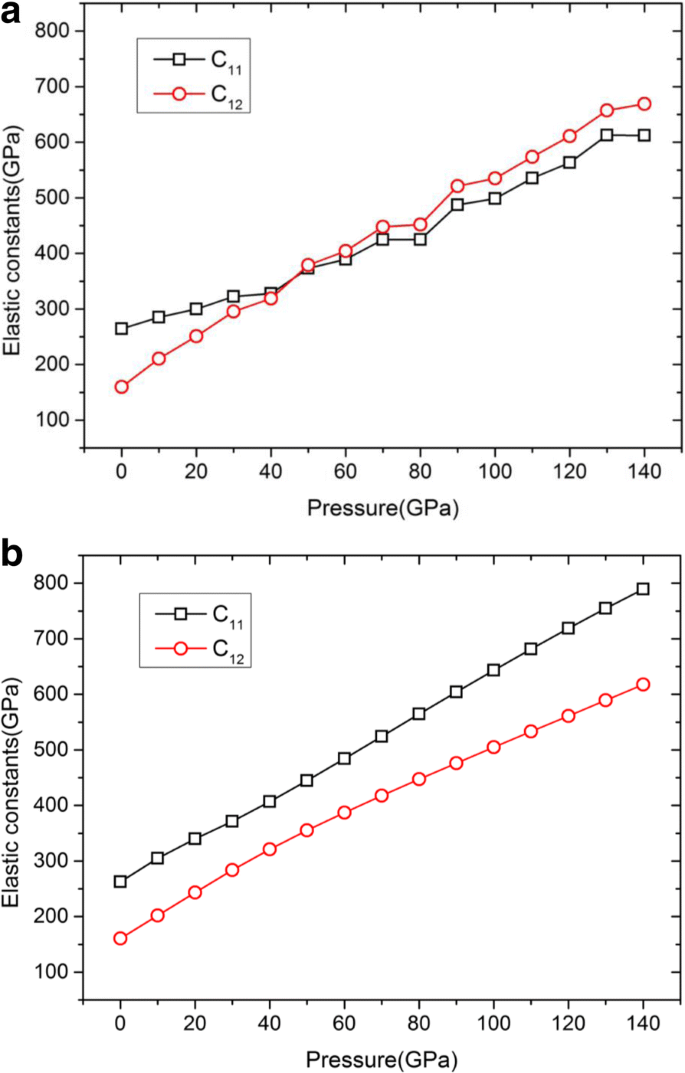
Druckabhängigkeit der elastischen Konstanten von C ₁₁ und C ₁₂ basierend auf den untersuchten Potenzialen. a Zhou-EAM. b Ravelo-EAM. In der vorliegenden Arbeit haben wir die direkte Methode verwendet, um die elastischen Konstanten C . zu berechnen ₁₁ und C ₁₂ für zwei Arten von EAM-Potentialen. Die C11/C12-Druckkurven für zwei Potentiale sind in a . dargestellt und b , bzw.

Aus Abb. 2a kann man entnehmen, dass die erhaltenen Kurven sowohl von C ₁₁ und C ₁₂ basierend auf dem Zhou-EAM-Potenzial kann mit dem zunehmenden Druck von bis zu 140 GPa nicht reibungslos weitergehen. Es gibt einen Übergangspunkt bei einem Druck von ~ 40 GPa, d. h. C ₁₁ = C ₁₂ , bei dem der Elastizitätsmodul von E ₁₀₀ wird nach Gl. (1). Außerdem E ₁₀₀ einen negativen Wert von mehr als 40 GPa darstellen, was verdächtig ist und den theoretischen und experimentellen Ergebnissen widerspricht [24, 25]. Daher schneidet das Zhou-EAM-Potenzial im hier betrachteten Bereich schlecht ab. Lassen Sie uns dann die Machbarkeit des Ravelo-EAM-Potenzials anhand der MD-Simulationsergebnisse von C . untersuchen ₁₁ und C ₁₂ basierend auf dem in Abb. 2b abgebildeten Ravelo-EAM-Potential. Numerische Ergebnisse zeigen, dass die Werte von C . umso größer sind, je höher der Druck ist ₁₁ und C ₁₂ , was gut mit dem Trend der sich mit dem Druck ändernden elastischen Konstanten durch DFT-Rechnungen übereinstimmt [9, 25]. Inzwischen sind die mit dem Ravelo-EAM-Potential berechneten Ergebnisse bemerkenswert, genauso wie die von Ruestes et al. [18]. Das Ravelo-EAM-Potential verhält sich unter hohem Druck gut und kann gleichzeitig auch die elastischen und mechanischen Eigenschaften von Ta unter dynamischer Verformung beschreiben [26]. Daher werden wir in den folgenden Abschnitten unsere Simulationen basierend auf dem Ravelo-EAM-Potenzial durchführen.

Nach der geometrischen Konstruktion führen wir eine Reihe relevanter MD-Simulationen durch. Bei den MD-Simulationen werden die periodischen Randbedingungen (PBC) in allen drei Richtungen der kubischen Modelle verwendet. Der Zeitschritt wird auf 1 fs und die Systemtemperatur auf 1.300, 600, 900, 1200 und 1500 K eingestellt, um die Temperaturabhängigkeit der elastischen Eigenschaften von Ta zu untersuchen. Zuerst wird das Modell unter Verwendung einer kanonischen Ensemble-MD-Simulation (NVT) um einen 50 ps-Relaxationsprozess entspannt, damit das System im lokalen Potenzialminimum liegt. Anschließend wurde eine isotherm-isobare (NPT) MD-Simulation verwendet, um einen spezifizierten hydrostatischen Druck im Bereich von 0 bis 140 GPa sicherzustellen, um die Auswirkungen des Drucks auf die elastischen Eigenschaften von Ta zu untersuchen [27]. Schließlich eine Zugbelastung mit einer Dehnungsrate von 5 × 10 ⁸ s ^− 1 bis 7,5 × 10 ⁹ s ^− 1 [28, 29] wird in x-Richtung von Ta kubisch angewendet. Währenddessen wird die NPT-Simulation in y- und z-Richtung mit dem gleichen Druck durchgeführt, der im zweiten Schritt aufgebracht wird. Daher gilt der hier berechnete Elastizitätsmodul für die <100>-Orientierung. Für alle MD-Simulationen werden die Modelle durch <100>Zugbelastung auf eine Dehnung von 15% in x-Richtung gestreckt.

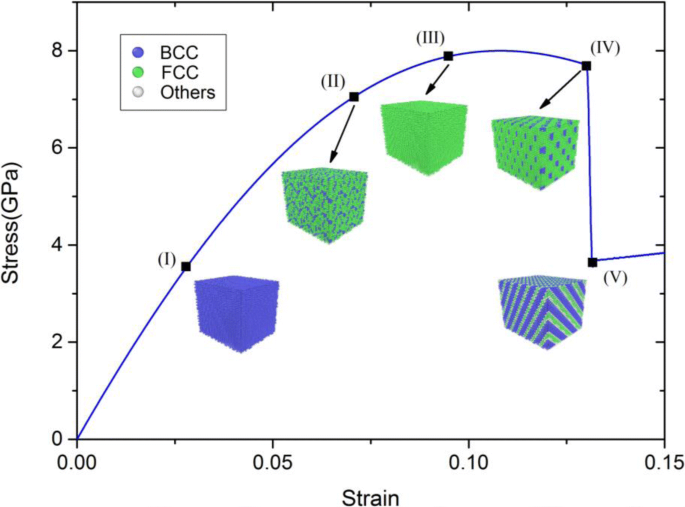
Spannungs-Dehnungs-Kurve von Ta bei Nulldruck und die entsprechenden Konfigurationen mit unterschiedlichen Dehnungen. Hinweise:Blaue, grüne und weiße Kugeln entsprechen BCC, FCC bzw. anderen Gitterstrukturen

Wie in Abb. 3 gezeigt, kann aus der Spannungs-Dehnungs-Kurve geschlossen werden, dass die Oberfläche in der Nähe der Konfiguration (IV) bricht. Zu Beginn der einachsigen Zugspannungen ändert sich die Spannung typischerweise linear mit der Dehnung und Abb. 3I zeigt, dass die atomaren Konfigurationen BCC-Strukturen beibehalten. Wenn die Dehnung zunimmt, beginnt der Phasenübergang von BCC- zu FCC-Strukturen bei einer Dehnung von ~ 7,4 % und endet bei einer Dehnung von ~ 9,8 %, wie in Abb. 3II bzw. II gezeigt. Und diese FCC-Strukturen halten das Maximum vor dem ersten Oberflächenbruch. Bei einer Dehnung von ~ 13,1% nehmen die Kantenlängen in y- und z-Richtung schlagartig ab, was zu einem Oberflächenbruch führt. Es ist bemerkenswert, dass Cluster in sehr kurzer Zeit auftreten, wie in Abb. 3IV gezeigt. Bei kontinuierlicher einachsiger Verformung bleibt die atomare Konfiguration streifenförmig, bis die Dehnung ~ 13,3% beträgt, was in Abb. 3V gezeigt ist.

In diesem Papier konzentrieren wir uns auf die Abhängigkeit der Zugeigenschaften von Modellgröße, Dehnungsrate, Temperatur und Druck, wie in diesem Abschnitt erörtert. Theoretisch wird das Modell im Stadium der elastischen Verformung linear gestreckt und der Elastizitätsmodul als Steigung des linearen Abschnitts der Spannungs-Dehnungs-Kurve definiert. Es zeigt sich, dass alle Modelle einen ähnlichen Streckprozess aufweisen und die Spannungs-Dehnungs-Kurven ähnliche Variationstendenzen aufweisen. Daher verwenden wir denselben Ansatz, um den Elastizitätsmodul von Ta verschiedener Modellgrößen und Dehnungsraten zu ermitteln.

Abhängigkeit von Größe und Belastungsrate

Tabelle 2 listet den Elastizitätsmodul und die Streckgrenze der verschiedenen Modellgrößen bei einer Temperatur von 1 K und einer Dehnungsrate von 5 × 10 ⁸ . auf s ^− 1 . Daraus lässt sich leicht schließen, dass die Modellgrößen keinen Einfluss auf den Elastizitätsmodul und die Fließspannung von Ta haben. Dies ist sehr einfach zu erklären, da der Elastizitätsmodul die Wechselwirkung zwischen Atomen beschreiben soll, während der Elastizitätsmodul nicht mit den Modellgrößen variiert. Aus Tabelle 2 ist ersichtlich, dass der Elastizitätsmodul ~ 139 GPa beträgt, was bemerkenswert dem Simulationsergebnis von 140 GPa entspricht [18].

Nach den bestehenden Refs. [28, 29], die meisten Dehnungsraten reichen von 10 ⁸ s ^− 1 bis 10 ¹⁰ s ^− 1 . In diesem Papier werden vier Dehnungsraten ausgewählt, um Zugsimulationen durchzuführen, einschließlich 5.0 × 10 ⁸ s ^− 1 , 7,5 × 10 ⁸ s ^− 1 , 5.0 × 10 ⁹ s ^− 1 , und 7,5 × 10 ⁹ s ^− 1 . Tabelle 3 listet den Elastizitätsmodul und die Streckgrenze bei einer Temperatur von 300 K und bei verschiedenen Dehnungsraten auf. Daraus kann leicht geschlossen werden, dass die Dehnungsrate keine offensichtlichen Auswirkungen auf den Elastizitätsmodul und die Fließspannung hat.

Inzwischen simulieren wir auch die Auswirkungen von Modellgröße und Dehnungsrate auf den Elastizitätsmodul und die Fließspannung unter verschiedenen Temperaturen und Drücken. Diese Simulationen kommen zum gleichen Ergebnis. Daher verwenden wir dieselbe Modellgröße von 3,96 nm und dieselbe Dehnungsrate von 5 × 10 ⁸ . s ^− 1 für die folgenden Simulationen.

Abhängigkeit von der Temperatur

Abbildung 4 zeigt die Spannungs-Dehnungs-Kurven bei verschiedenen Temperaturen bis 1500 K. Es ist zu erkennen, dass die Steigungen dieser Kurven, die den Elastizitätsmodul in <100>-Orientierung bezeichnen, d. h. E ₁₀₀ , während der elastischen Zugperiode und die Streckspannung nehmen mit steigender Temperatur allmählich ab. Nach der Theorie der Thermodynamik [31] erfüllt die gesamte kinetische Energie aller Atome des Systems im Allgemeinen die folgende Gleichung:

wo E _k die kinetische Gesamtenergie des Systems ist; N ist die Gesamtzahl der Atome; K _B ist die Boltzmann-Konstante; T ist die thermodynamische Temperatur. Daraus kann geschlossen werden, dass das System mit der höheren Temperatur eine größere kinetische Gesamtenergie enthält und sich die Atome schneller bewegen. Aus thermodynamischer Sicht werden die Atome aktiver und die Bewegung der Atome intensiver, was eine größere Amplitude in ihrer Gleichgewichtslage bedeutet. Beim Streckprozess wird die Anziehungskraft zwischen Atomen relativ reduziert und Atome entweichen leicht aus der Gleichgewichtslage, so dass die Spannung in x-Richtung bei gleicher Dehnung abnimmt. Daher ist der Elastizitätsmodul bei höherer Temperatur geringer als bei niedrigerer Temperatur. Darüber hinaus stimmt der Trend dieser Kurven gut mit frühen theoretischen und experimentellen Ergebnissen von Ta überein [6, 7, 32].

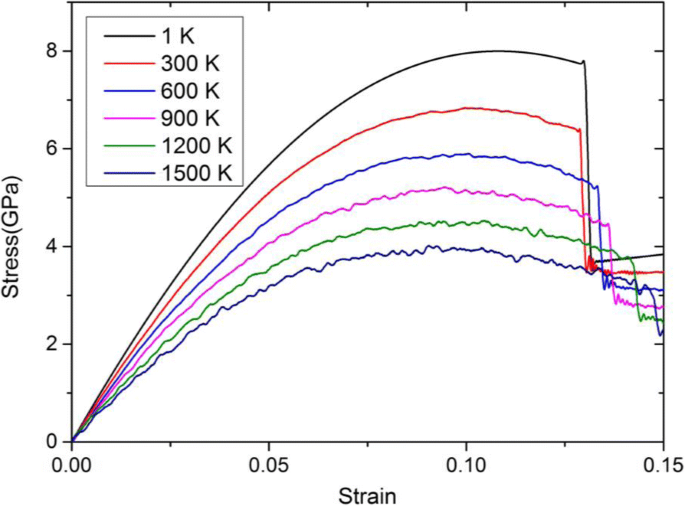
Spannungs-Dehnungs-Kurven des 3,96-nm-Ta-Modells bei einer Dehnungsrate von 5 × 10 ⁸ s ^− 1 und unterschiedliche Temperaturen von 1 bis 1500 K. Aus Fig. 4 ist ersichtlich, dass die Steigungen dieser Kurven, die den Elastizitätsmodul in <100>-Orientierung bezeichnen, d. h. E ₁₀₀ , während der elastischen Zugperiode und die Streckgrenze nehmen mit steigender Temperatur allmählich ab

Um die Beobachtung zu erleichtern, listet Tabelle 4 den Elastizitätsmodul und die Fließspannung von Ta bei verschiedenen Temperaturen auf. Der Elastizitätsmodul sinkt um ~ 42,3 % von 136,49 auf 76,67 GPa und die Streckgrenze sinkt um ~ 51 % von ~ 8 auf ~ 4 GPa, wenn die Temperatur von 1 auf 1500 K steigt.

Gemäß Tabelle 4 können wir weiter eine Parametrisierung der Temperaturabhängigkeit des Elastizitätsmoduls (E ₁₀₀ ) Ergebnisse als durchgezogene Linie in Abb. 5a dargestellt. Die Parametrierung lautet wie folgt:

$$ {E}_{100}=a+{b}^{\ast}T $$ (3)

wo E ₁₀₀ ist in (GPa) und T wird in (K ); a = 138,07 ± 0,92111 und b = − 0,04094 ± 0,00101. Diese Gleichung zeigt, dass E ₁₀₀ nimmt mit steigender Temperatur linear ab und wird für den Einsatz bis zu einer Temperatur von 0 bis 1500 K empfohlen. Aus Gl. (3), kann leicht erhalten werden, dass E ₁₀₀ erreicht 0 GPa bei einer Temperatur von T _kritisch = −a /b = 3372 K, was der Schmelztemperatur von Ta sehr nahe kommt [15].

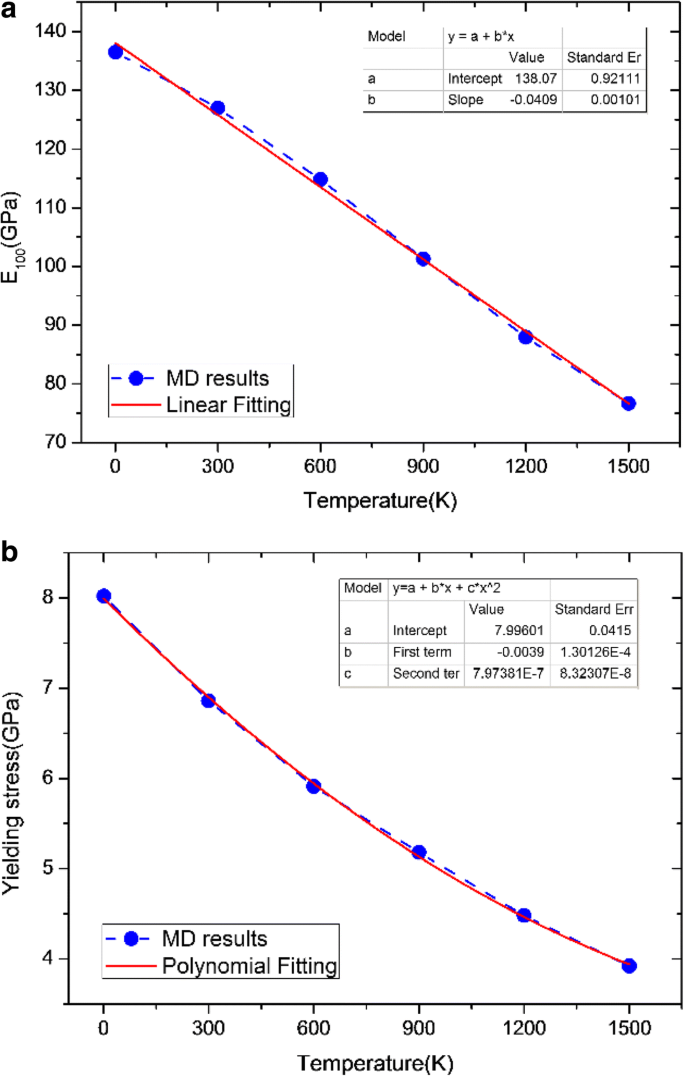
a Elastizitätsmodul und b Streckspannung gegen Temperatur für Ta. In Abb. 5 präsentieren wir auch eine Parametrisierung der Temperaturabhängigkeit des Elastizitätsmoduls (E ₁₀₀ ) Ergebnisse

Für die Streckgrenze ist die empfohlene Parametrisierung

$$ {Y}_{\mathrm{Belastung}}=a+{b}^{\ast}T+{c}^{\ast }{T}^2 $$ (4)

wobei Y _Stress ist in (GPa) und T wird in (K ); a =7,99610 ± 0,0415, b = − 0,0039 ± 1,30126 × 10 ^− 4 , und c =7,97381 × 10 ^− 7 ± 8,32307 × 10 ^− 8 . Aus Gl. (4) kann festgestellt werden, dass die Fließspannung wahrscheinlich mit der Temperatur abnimmt, die einem quadratischen Polynommodell entspricht, wie in Abb. 5b als durchgezogene Linie angegeben.

Abhängigkeit vom Druck

Wie im Abschnitt „Einführung“ erwähnt, wurden umfangreiche theoretische und experimentelle Anstrengungen zu den thermoelastischen Eigenschaften von Ta unter Hochdruckbedingungen unternommen. Im Gegensatz zu den statischen Methoden wenden wir eine dynamische Methode durch <100> Zugbelastung an, um die Druckabhängigkeit des Elastizitätsmoduls von E . zu untersuchen ₁₀₀ unter unterschiedlichem hydrostatischem Druck.

Abbildung 6 zeigt die Kurven des Elastizitätsmoduls von E ₁₀₀ gegen den Druck bis zu 140 GPa bei verschiedenen Temperaturen von 1 bis 1500 K. Während alle durchgezogenen Linien mit unterschiedlichen Farben durch ein dynamisches Verfahren bei verschiedenen Temperaturen erhalten werden, wird die gestrichelte Linie mit quadratischen Markierungen durch ein statisches Verfahren unter Verwendung von Gl. (1) basierend auf den Werten von C ₁₁ und C ₁₂ bei 0 K. Es ist offensichtlich, dass die Kurve bei 1 K, d Arbeit ist bei hohem Druck bis zu 140 GPa anwendbar.

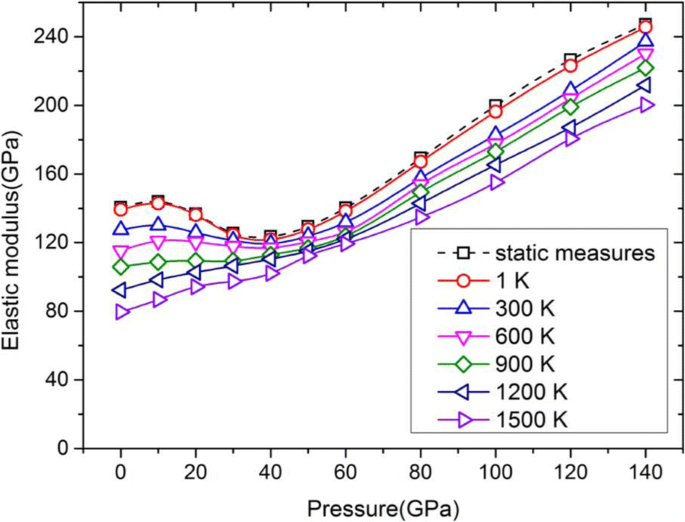
Elastizitätsmodul in <100> Orientierung von Ta bei verschiedenen Temperaturen und Drücken. Es ist erwähnenswert, dass der Elastizitätsmodul dieser Kurven E . ist ₁₀₀

Wie in Abb. 6 dargestellt, ist der Elastizitätsmodul von E ₁₀₀ bei einer Temperatur von nicht mehr als 600 K zeigt einen nach unten gerichteten konkaven Abschnitt, wenn der Druck von 20 auf 60 GPa ansteigt. Rüste et al. [18] berichteten unter Verwendung von MD-Simulationen über die elastischen Konstanten als Funktion des Drucks bis zu 60 GPa, und die Ergebnisse stimmen gut mit dem berechneten C . überein ₁₁ und C ₁₂ im vorliegenden Werk. Im Gegenzug wird der berechnete Elastizitätsmodul von E ₁₀₀ zeigt auch bei unseren Ergebnissen den gleichen Trend. Aber der berechnete Elastizitätsmodul von E ₁₀₀ aus DFT-Rechnungen [33] nimmt mit zunehmendem Druck allmählich zu, und in den Kurven wird kein nach unten konkaver Abschnitt gefunden. Wie kommt es zu dieser Inkonsistenz? Im Allgemeinen werden die in MD-Simulationen verwendeten Potenziale durch Anpassung von DFT-Rechnungen und experimentellen Ergebnissen erhalten. In diesem Sinne haben DFT-Berechnungen eine höhere Genauigkeit als die MD-Methode. Das Ravelo-EAM-Potential [21] wird konstruiert, indem Hochdruckeigenschaften in die passende DFT-Zustandsgleichungskurve (EOS) von Ta-Einkristallen eingeführt werden. Während des Anpassungsverfahrens wird die kalte Kurve von EOS erweitert, um Terme höherer Ordnung (kubisch und quartär) der Gitterkonstanten einzuschließen, was MD EOS sehr empfindlich gegenüber Termen der Gitterkonstanten höherer Ordnung macht. Mit anderen Worten, diese Inkonsistenz könnte darauf zurückzuführen sein, dass das Ravelo-EAM-Potenzial den EOS von Ta unter dem Druck von 20 bis 60 GPa nicht genau beschreiben konnte. Insgesamt kann gefolgert werden, dass die Kurven des Elastizitätsmoduls gegenüber dem Druck bei unterschiedlichen Temperaturen einen ähnlichen Trend aufweisen und der Elastizitätsmodul mit steigendem Druck über ~ 40 GPa allmählich ansteigt.