Molekulardynamiksimulation des Zerspanmechanismus im Hybridbearbeitungsprozess von einkristallinem Silizium

Einführung

Einkristallines Silizium ist ein wichtiges Halbleitermaterial, das aufgrund seiner hervorragenden optischen und mechanischen Eigenschaften in der Infrarotoptik, Mikroelektronik und Optoelektronik weit verbreitet ist [1, 2]. Aufgrund der Härte und Sprödigkeit von einkristallinem Silizium können jedoch während der mechanischen Bearbeitung mikroskopische Sprödbrüche und Schäden unter der Oberfläche erzeugt werden. Während des Mikrofräsprozesses können bearbeitungsbedingte Innenkantenausbrüche im Werkstück erzeugt werden [3]. Bei der Bearbeitung mit einkristallinem Diamantschneiden (SPDT) kann je nach Bearbeitungsparameter eine Schadschicht im Bereich von 200 bis 600 nm gebildet werden [4, 5]. Obwohl die Schadensschicht unter der Oberfläche durch Schleifen und Polieren auf etwa 50 nm verringert werden kann. Die Bearbeitungseffizienz und die Fähigkeit zur Herstellung komplexer Strukturen sind begrenzt. Um diese Probleme zu überwinden, wurden verschiedene unterstützende Bearbeitungstechnologien vorgeschlagen und getestet. Insbesondere das thermisch unterstützte Schneiden (TAC) [6] und das vibrationsunterstützte Schneiden (VAC) [7] haben aufgrund ihrer außergewöhnlichen Schneidleistung breite Aufmerksamkeit auf sich gezogen.

Bei spröden Werkstoffen wie einkristallinem Silizium kann der Übergang von spröde zu duktil durch eine Erhöhung der Bearbeitungstemperatur gefördert werden. Beim TAC-Prozess wird das Silizium-Werkstück thermisch erweicht, was eine Abnahme der Schnittkräfte [8] und der spezifischen Schnittenergie [9, 10] zur Folge hat. Unterdessen wird das Glühen der Hochdruckphasen in die kubische Siliziumphase sichtbar, wenn die Bearbeitungstemperatur erhöht wird [11]. Bei entsprechender Wahl der Bearbeitungsparameter kann durch TAC die gewünschte bearbeitete Oberfläche mit hoher Phasenreinheit und geringer Beschädigung unter der Oberfläche erreicht werden [12,13,14]. Neben der TAC ist das vibrationsunterstützte Schneiden (VAC) eine weitere fördernde Methode, um eine hochwertige Oberfläche auf einkristallinem Silizium zu erzielen. Diese Technik wird in der verarbeitenden Industrie seit den 1960er Jahren angewendet [15]. In der frühen Entwicklung dieser Technologie wird in der Zerspanung nur eine lineare Schwingungsbewegung in Nennschneidrichtung praktiziert, die als Linear Vibration Cutting (LVC) bezeichnet wird. 1994 wurde das elliptische Vibrationsschneiden (EVC) von Shamoto und Moriwaki [16] vorgeschlagen. Im Folgenden wurde die Zerspanbarkeit von EVC auf vielen spröden Materialien wie Silizium [17, 18], reaktionsgebundenem Siliziumkarbid [7], Wolframkarbid [19, 20] und gehärtetem Stahl [21] überprüft. Während des EVC-Prozesses können die Schäden unter der Oberfläche effektiv unterdrückt werden, da die transiente Schnitttiefe (DOC) viel kleiner ist als die nominale DOC [22]. Außerdem werden die Kontaktflächen zwischen Schneidwerkzeug und Werkstück aufgrund der Trennung in jedem Vibrationszyklus dem umgebenden Gas oder Fluid ausgesetzt, das die erzeugte Schneidwärme abführt. Daher kann der Verschleiß von Schneidwerkzeugen wie Adhäsion und thermochemische Reaktionen [23] effektiv unterdrückt werden.

Um die Zerspanbarkeit spröder Materialien weiter zu verbessern, wurden Experimente zur Hybridbearbeitung (HM) durchgeführt, bei denen der thermische und der Schwingungsassistent kombiniert wurden [24, 25]. Es wurde festgestellt, dass beim Schneiden von Inconel 718 durch das HM-Verfahren die bearbeitete Oberflächenrauheit effektiv verringert werden kann [26]. Durch Experimente und Finite-Elemente-Methode (FEM)-Simulationen kann beim HM-Prozess eine deutliche Reduzierung der Schnittkräfte und eine überlegene Oberflächengüte von Titanlegierungen erreicht werden [27]. Diese Ergebnisse demonstrieren die Durchführbarkeit des HM-Verfahrens bei der Präzisionsbearbeitung spröder Materialien. Es ist jedoch schwierig, die physikalischen Größen während des Bearbeitungsprozesses direkt zu beobachten und zu messen, da das Schneidwerkzeug mit hoher Frequenz vibriert und die Verformungszone eine hohe Temperatur hat. Darüber hinaus reicht bei der nanometrischen Oberflächenherstellung die vorübergehende Materialabtragsdicke normalerweise von Sub-Nanometern bis zu einigen Nanometern. Daher ist die traditionelle Kontinuumsdarstellung des Problems wie FEM fragwürdig, da die quantenmechanischen Effekte offensichtlich werden.

In den letzten Jahren wurde die Molekulardynamik (MD)-Simulation aufgrund ihrer Vorteile bei der Untersuchung von nanometrischen Schneidprozessen bei Untersuchungen des unterstützenden Bearbeitungsprozesses weit verbreitet [28,29,30]. Basierend auf früheren Simulationen von TAC [31] wird bei einer Erhöhung der Schnitttemperatur die Anisotropie der Schnittkraft, der spezifischen Schnittenergie und der Fließspannung deutlicher. Währenddessen ist die Scherkraft im Werkstück bei höherer Schnitttemperatur geringer, was zu engeren Scherzonen und größeren Scherebenenwinkeln führt [32]. Außerdem kann das Zeitspanvolumen mit steigender Schnitttemperatur verbessert werden, da mehr Späne entstehen [33]. Für den EVC-Prozess wurde durch MD-Simulation festgestellt, dass die Druckspannung und die Scherspannung im Deformationsbereich im Vergleich zum gewöhnlichen Schneiden stark verringert werden können [34], was für die Unterdrückung von Schäden unter der Oberfläche von Vorteil ist. Außerdem zeigt der EVC-Prozess eine deutliche Ausdünnung der Schneidspäne, was zu einer Erhöhung des Verhältnisses von ungeschnittener Spandicke zu geschnittener Spandicke führt [35]. Darüber hinaus wurde enthüllt, dass die Schwingungsparameter einschließlich Amplitudenverhältnisse, Schwingungsfrequenzen und Phasendifferenzen großen Einfluss auf die Abtragsleistung haben [34, 36].

Diese bemerkenswerten Errungenschaften haben das Verständnis des Bearbeitungsmechanismus für den unterstützenden Bearbeitungsprozess verbessert. Um Rechenzeit und Speicher zu sparen, sind die Simulationssysteme jedoch meist recht klein. In früheren Simulationen des EVC-Prozesses liegen die Schwingungsamplituden und der nominale DOC unter 5 nm [22, 36]. Daher beträgt die vorübergehende Materialabtragsdicke normalerweise weniger als 1 nm, was den tatsächlichen Materialabtragsprozess nicht genau beschreibt. Darüber hinaus wurde nicht über die MD-Simulationen des HM-Prozesses berichtet. Der Mechanismus des Materialabtragsprozesses und der Schadensbildung unter der Oberfläche während des HM-Prozesses ist noch unklar. Daher wird in diesem Beitrag eine MD-Simulation durchgeführt, um den Schneidmechanismus des HM-Prozesses aufzuzeigen. Das klassische Schnittmodell wird dahingehend modifiziert, dass die Schwingungsparameter viel näher an den experimentellen Werten liegen, z. Der Abtragsmechanismus in einem Schwingzyklus und der Einfluss einer erhöhten Schnitttemperatur werden untersucht. Die MD-Simulation wird mit dem berühmten Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) durchgeführt [37]. Zur Analyse der Simulationsergebnisse wird die Nachbearbeitungssoftware OVITO [38] verwendet.

Simulationsmethode

Details zum Schnittmodell

Abbildung 1 zeigt das schematische Diagramm des EVC-Prozesses, der ursprünglich von Shamoto et al. vorgestellt wurde. [39]. Die Werkzeugbahn kann wie folgt ausgedrückt werden:

wo x (t ) und z (t ) repräsentieren die Schneidwerkzeugverschiebung im x und z Richtungen. A _c und A _d sind die Schwingungsamplituden in Nenn-Schnittrichtung (x Richtung) und die nominelle DOC-Richtung (negativ z Richtung). Parameter f , v , φ , und t repräsentieren die Vibrationsfrequenz, die nominale Schnittgeschwindigkeit, die Phasendifferenz bzw. die Simulationszeit. Die Simulationszeit t _ich repräsentiert die Zeit des Punktes P _ich auf der Werkzeugbahn aus Abb. 1.

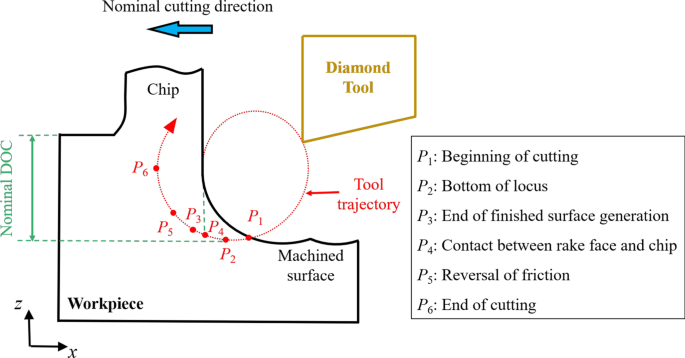
Das schematische Diagramm des EVC-Prozesses

Gemäß der geometrischen Beziehung [40] ist der Wert von t ₁ und t ₃ kann bestimmt werden durch:

Dann, t ₆ kann erreicht werden, wenn die vorübergehende Bewegungsrichtung des Diamantwerkzeugs parallel zur Werkzeugspanfläche ist:

wo γ ist der Spanwinkel des Diamantschneidwerkzeugs.

Das MD-Modell ist in Abb. 2 dargestellt. Das einkristalline Siliziumwerkstück wird als verformbarer Körper eingesetzt. Während das Diamantwerkzeug als starrer Körper betrachtet wird, kann der Werkzeugverschleiß in dieser Simulation vernachlässigt werden. Die Morphologie des Werkstücks im klassischen Schnittmodell wird entsprechend der Werkzeugtrajektorie im vorherigen Vibrationszyklus unter Berücksichtigung des Schneidenradius umgeformt. Die Werkzeugtrajektorie kann wie in Fig. 2b veranschaulicht bestimmt werden. P _o und P _b sind der Mittelpunkt und der unterste Punkt des Schneidenkreises. Wenn der Werkzeugkanteneffekt berücksichtigt wird, ist der Übergangsflächenerzeugungspunkt P _c während der Werkzeugbewegung entlang der Werkzeugschneide variiert. Die eigentliche fertige Oberfläche wird durch die Hülllinie der Schneide erzeugt. Wenn die Flugbahn von P _b wird durch Gl. (1) und (2), die Flugbahn von P _c kann berechnet werden durch [41]:

wo

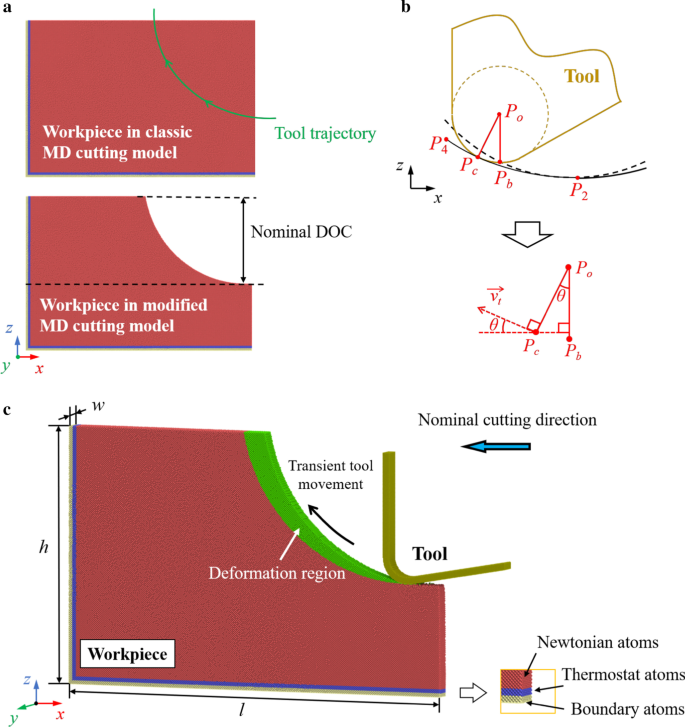
Schema des MD-Schnittmodells. a Modifikation des Werkstücks. b Bestimmung der Werkzeugbahn. c Die Morphologie des modifizierten MD-Modells. Grüne Atome repräsentieren den Deformationsbereich in einem Schwingungszyklus

Siliziumatome werden in drei Gruppen eingeteilt:Grenzatome, Thermostatatome und Newtonsche Atome. Die Grenzatome werden in ihren ausbalancierten Positionen fixiert, um das Werkstück während der Simulation zu halten. Die Thermostatatome werden auf Umgebungstemperatur gehalten, um die erzeugte Schneidwärme abzuleiten, während die Newtonschen Atome dem zweiten Newtonschen Gesetz folgen.

Einzelheiten zu den Simulationsparametern sind in Tabelle 1 aufgeführt. Die Länge l und Höhe h wurden bestimmt, um einen ausreichenden Abstand zwischen der Schneidzone und den festen Begrenzungen einzuhalten. Die periodische Randbedingung wird entlang des y . angewendet Richtung, um Bulk-Silizium zu imitieren. Die nominelle Schnittrichtung, der Span-/Freiwinkel und die Phasendifferenz wurden anhand des Versuchsaufbaus bestimmt [42]. Die Schwingungsamplitude und der nominale DOC werden vergrößert, um sich mit akzeptablen Simulationskosten dem experimentellen Maßstab anzunähern. Um die Dicke des entfernten Materials (grüne Atome in Abb. 2c) sicherzustellen, wurden das Geschwindigkeitsverhältnis und die Vibrationsfrequenz auf 40 bzw. 500 MHz eingestellt. Daher wurde die nominelle Schnittgeschwindigkeit mit 3,125 m/s festgelegt. Darüber hinaus werden Simulationen mit unterschiedlichen Schneidtemperaturen durchgeführt, um die Wirkung des thermischen Assistenten auf den Schneidmechanismus aufzuzeigen. Die Schnitttemperatur wird von 300 auf 1200 K erhöht, was während der TAC-wie laserunterstützten Bearbeitung realisierbar ist [4, 11].

In diesem modifizierten Modell wird nur die Schneidphase während des Vibrationszyklus simuliert und die Zeitschritte beim Trennen des Werkstücks mit Schneidwerkzeug gespeichert. Daher kann die Rechenleistung auf den transienten Schneidprozess konzentriert werden. Am wichtigsten ist, dass der vorübergehende Materialabtragsprozess genau beschrieben werden kann. Tabelle 2 zeigt einen Vergleich zwischen dem modifizierten Modell und dem klassischen MD-Modell.

Potenzielle Funktion

Bei der MD-Simulation ist es wichtig, ein robustes Potenzial zu verwenden, um die Wechselwirkung zwischen Atomen zu beschreiben. Für einkristallines Silizium haben Wissenschaftler viele Potenziale entwickelt, wie die modifizierte Embedded-Atom-Methode (MEAM) [45], Stillinger-Weber (SW) [46], Tersoff [47] und die ladungsoptimierte Vielteilchenmethode (COMB) [ 48] Potenziale. Unter diesen Potentialen hat das analytische Bindungsordnungspotential (ABOP) von Erhart und Albe [49] zunehmende Aufmerksamkeit auf sich gezogen. Es handelt sich um eine Drei-Körper-Potentialfunktion, die die Bildung und das Aufbrechen von Bindungen während der Bearbeitungssimulation ermöglicht. Nach früheren Untersuchungen [50] kann der ABOP sowohl die Dimer- als auch die Volumeneigenschaften von Silizium genau beschreiben. Inzwischen stimmen die mechanischen Eigenschaften von Silizium, das mit dem ABOP hergestellt wurde, gut mit den Experimenten überein [31], was für MD-Simulationen der nanoskaligen Bearbeitung wichtig ist. Daher wird in dieser Arbeit das ABOP-Potential verwendet, um die Silizium-Silizium- und Kohlenstoff-Kohlenstoff-Wechselwirkungen zu beschreiben. Inzwischen wird die Wechselwirkung von Silizium-Kohlenstoff durch das Morsepotential beschrieben, das sich in der nanoskaligen Schneidsimulation als effizientes Potential erwiesen hat [51, 52]. Die Morsepotentialfunktion kann wie folgt ausgedrückt werden:

wo D _M , a, und R _M repräsentiert die Kohäsionsenergie, das Elastizitätsmodul bzw. den Gleichgewichtsabstand zwischen den Atomen. Die Parameter für das Morsepotential sind [53]:D _M = 0,435 eV, a = 46.487 nm ⁻¹ , R _M = 0,19475 nm.

Ergebnisse und Diskussion

Schnittleistung

Bei der normalen Zerspanung kann der dominierende Materialabtragsmechanismus stark durch die unverformte Spandicke beeinflusst werden [54]. Bei kleinen unverformten Spandicken ist der vorherrschende Materialabtragsmechanismus die Extrusion. Die metallische stabile Phase (Si-II) kann durch den Hochdruckphasenübergang (HPPT) erzeugt werden, der die duktile Verformung von Silizium erleichtert. Bei Erhöhung der unverformten Spandicke kann das Material hauptsächlich durch Scherprozesse abgetragen werden. Da sich beim EVC-Prozess die Dicke des unverformten Spans ständig ändert, kann der Materialabtragsmechanismus in einem Vibrationszyklus vom Extrudieren zum Scheren übergehen. Abbildung 3 zeigt die Momentaufnahmen der Schnittsimulation bei 300 K. Die Kristallstruktur des Werkstücks wird durch die Common Neighbor Analysis (CNA) bestimmt [55]. Diese Analyse findet Atome, die in einem kubischen oder hexagonalen Diamantgitter angeordnet sind. Die Nicht-Diamant-Struktur in Abb. 3c, e enthält hauptsächlich die amorphe Phase (a-Si), Si-II und andere defekte Atome [56]. Diese Strukturen sind instabil und wandeln sich nach dem Schneiden in a-Si um. Aus Fig. 3b, c ist ersichtlich, dass das Material in der anfänglichen Schneidephase hauptsächlich durch Extrusion entfernt wird. In der Nähe der Werkzeugschneide ist ein vorübergehender Stagnationspunkt zu beobachten. Ähnlich wie beim gewöhnlichen Schneiden werden Materialien im Verformungsbereich durch den Staupunkt in Späne und komprimiertes Material geteilt. Mit fortschreitendem Schneidwerkzeug wird die unverformte Spandicke erhöht. Scherebenen und polykristalline Körner werden im Werkstück erzeugt, was darauf hindeutet, dass das Scheren zum vorherrschenden Materialabtragsmechanismus wird.

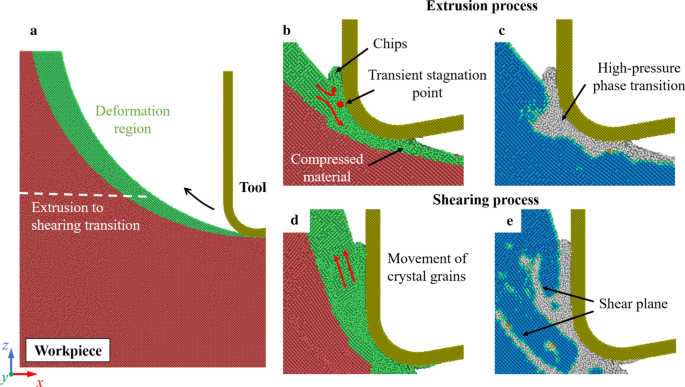
Übergang des Materialabtragsmechanismus. a Darstellung des Verformungsbereichs. b , d Extrusions- und Scherverfahren. c , e Identifizierung der Kristallstruktur im Werkstück. Blaue Atome repräsentieren die kubische Diamantstruktur, während sich die grauen Atome in der Nicht-Diamantstruktur befinden

Abbildung 4 zeigt die Werkstückmorphologie bei verschiedenen Schnitttemperaturen. Bei 300 K können während der Aufwärtsbewegung des Werkzeugs deutliche Risse und Brüche im Werkstück beobachtet werden. Bei spröden Materialien wie einkristallinem Silizium würde die Aufwärtsbewegung des Werkzeugs zu Materialabrissen und Fehlern im Werkstück führen, was in der EVC als spezifisches Problem betrachtet wird [42]. Obwohl diese Risse durch weitere Vibrationszyklen beseitigt werden können, wird die Bearbeitungsstabilität durch die Unregelmäßigkeit der Werkstückoberfläche beeinträchtigt. Wenn die Schnitttemperatur erhöht wird, wird die Erzeugung und Ausbreitung von Rissen wirksam unterdrückt. Aus Abb. 4d wird kein offensichtlicher Bruch erkannt, wenn die Schnitttemperatur auf 1200 K ansteigt. Es wird jedoch beobachtet, dass bei 900 K und 1200 K ein Anschwellen der bearbeiteten Oberfläche offensichtlich wird, wenn der Materialabtragsmechanismus in Scherung umgewandelt wird. Daraus kann geschlossen werden, dass das Quellen durch die Rotation dieser Kristallkörner bei hoher Temperatur verursacht werden kann, wenn mehr Kristallkörner in der Scherstufe erzeugt werden.

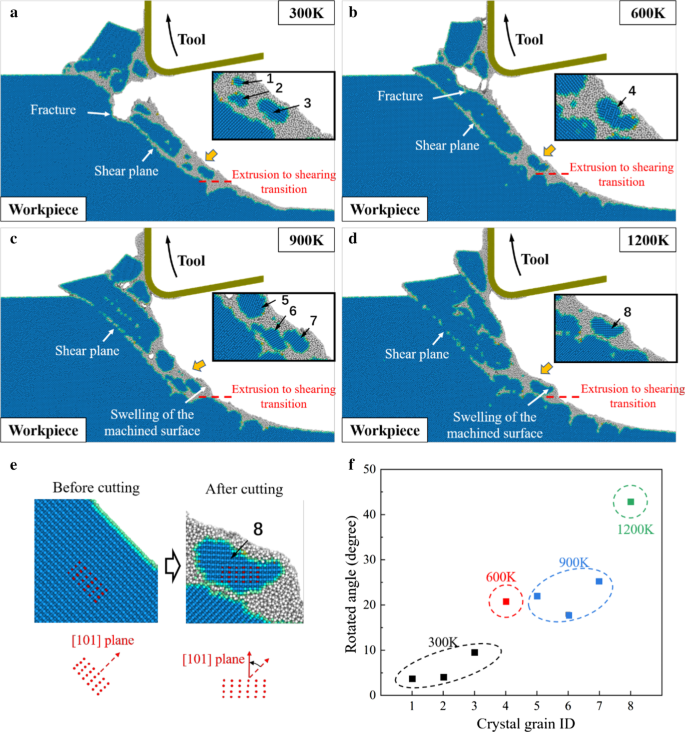
Werkstückmorphologie des HM-Prozesses bei a 300 K. b 600 K. c 900 K. Tag 1200 K. Blaue Atome stellen die kubische Diamantstruktur dar, während die grauen Atome eine Nicht-Diamantstruktur aufweisen. e Bestimmung des Rotationswinkels von Kristallkörnern. f Der Drehwinkel bei steigender Schnitttemperatur

Zur klaren Beschreibung dieser Drehung werden die Koordinaten von 24 markierten Atomen (rote Atome) in den Kristallkörnern verwendet, um den durchschnittlichen Drehwinkel zu berechnen, wie in Abb. 4e dargestellt. Der Rotationswinkel von 8 Kristallkörnern (nummeriert in Abb. 4a–d) ist in Abb. 4f zusammengefasst. Es kann beobachtet werden, dass der Drehwinkel bei erhöhter Temperatur offensichtlich erhöht wird. Während des HM-Prozesses kann die Viskosität von a-Si bei hoher Temperatur stark verringert werden und die Hochziehbewegung der Werkstückatome wird durch die Aufwärtsbewegung des Werkzeugs gefördert. Daher wird der Atomstrom im Werkstück verbessert und die Rotation der Kristallkörner kann erleichtert werden, was zum Aufquellen der bearbeiteten Oberfläche führt. Um die Rotation der Kristallkörner einzuschränken, sollte die Heizleistung kontrolliert werden, um eine Überhitzung des Werkstücks zu vermeiden. Außerdem sollten die Schwingungsparameter sorgfältig gewählt werden, z. B. sollten kleinere Nennschnittgeschwindigkeiten und höhere Schwingungsfrequenzen angewendet werden, um die Bildung von Kristallkörnern zu unterdrücken und das Aufquellen durch weitere Schwingungszyklen zu beseitigen. Wie in Abb. 5 dargestellt, mit geeigneten Schwingungsparametern P ₁ in der Extrusionsphase lokalisieren und die fertig bearbeitete Oberfläche wird durch Extrusion ohne Quellung erzeugt.

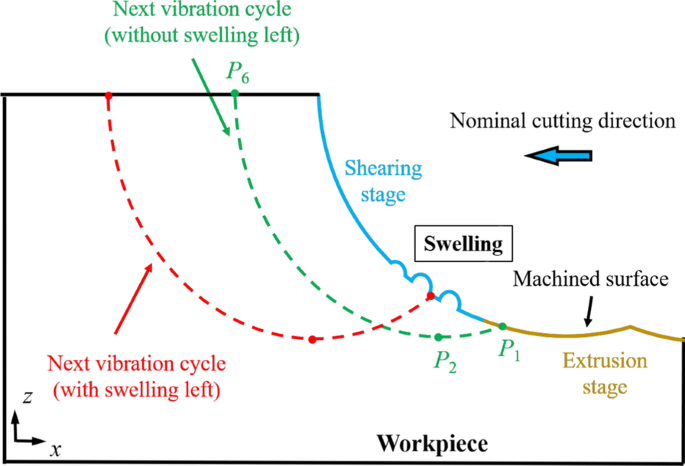
Beseitigung der Quellung im HM-Verfahren

Spannungsfeld im Werkstück

Um den Schneidmechanismus während des HM-Prozesses weiter zu untersuchen, wurde die Spannungsverteilung im Werkstück berechnet. In der MD-Simulation kann die hydrostatische Belastung wie folgt ausgedrückt werden:

wo σ _x , σ _y , und σ _z , sind Spannungstensoren aus LAMMPS-Ausgabedaten.

Die hydrostatische Spannungsverteilung während der Extrusions- und Scherphasen ist in Abb. 6 dargestellt. Die Spitzenwerte der Spannungen im Druck- und Zugbereich wurden markiert. Mit der Werkzeugbewegung verändert sich der Kontaktpunkt zwischen Werkzeug und Werkstück entlang des Schneidenzyklus, was zur Bewegung des Druckbereichs von der Werkzeugschneide zur Spanfläche führt. Nach früheren Berichten könnte die HPPT von der einkristallinen Siliziumphase (Si-I) zu Si-II bei Drücken ab 10–12 GPa erfolgen [57, 58]. In der Schnittsimulation bei 300 K erreichte die maximale Druckspannung in der Extrusions- und Scherphase 18,1 GPa bzw. 17,6 GPa. Dieses Ergebnis zeigt, dass die duktile Si-II-Phase während des Schneidens erzeugt werden kann und das HPPT noch in der Scherphase existiert. Darüber hinaus konzentriert sich die Zugspannung in der Extrusionsphase hauptsächlich in der Nähe des Kontaktbereichs zwischen der Werkzeugflankenfläche und der bearbeiteten Oberfläche als Ergebnis der Adhäsion von Siliziumatomen und der Werkzeugoberfläche. Wenn das Werkzeug in die Scherphase übergeht, wird der Zugbereich vergrößert und die Zugspannungskonzentration im unterirdischen Werkstück wird stark erhöht, was durch die Hochziehbewegung verursacht wird. Wenn die Schnitttemperatur erhöht wird, wird die plastische Verformbarkeit von einkristallinem Silizium verbessert und innere Spannungen im Werkstück verringert. Wenn die Temperatur von 300 auf 1200 K ansteigt, nahm die maximale Druckspannung in der Extrusions- und Scherphase um 16,6 % und 25 % ab. Obwohl die Zugspannungskonzentration in dem Werkstück unter der Oberfläche immer noch offensichtlich ist, ist der Spitzenwert der Zugspannung offensichtlich um mehr als 30% verringert. Es wurde berichtet, dass die Bruchzähigkeit von einkristallinem Silizium bei höheren Temperaturen effektiv erhöht werden kann [59]. Daher können Risse und Brüche, die durch den Abrisseffekt aufgrund der Aufwärtsbewegung des Werkzeugs verursacht werden, effektiv unterdrückt werden.

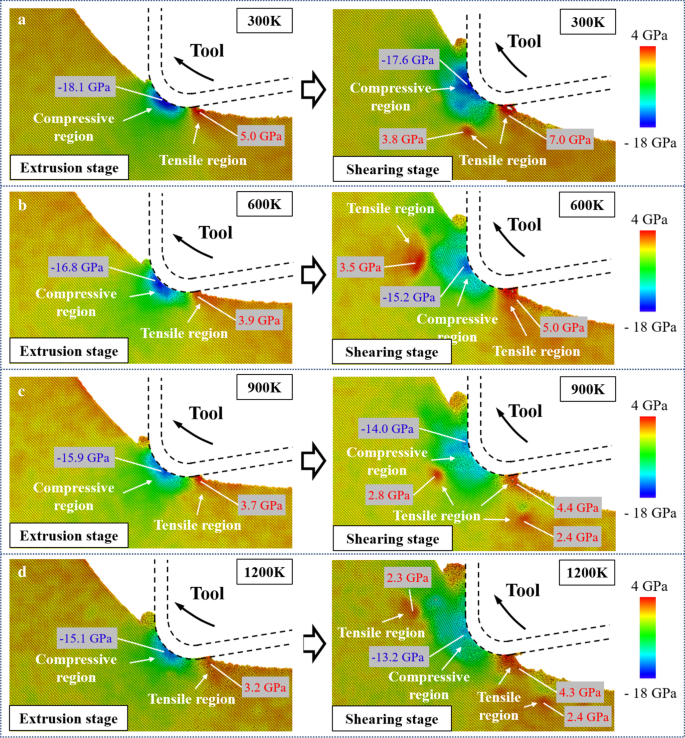
Die hydrostatische Spannungsverteilung bei:a 300 K. b 600 K. c 900 K. Tag 1200 K

Einkristallines Silizium hat eine Face Center Cubic (FCC) Kristallstruktur mit 12 Gleitsystemen. Basierend auf der Werkzeugbewegung sind die wichtigsten Gleitsysteme für die Schubverformung die (111)/[\(\stackrel{\mathrm{-}}{1}\)01] und (1\(\stackrel{\mathrm{- }}{1}\)1)/[\(\stackrel{\mathrm{-}}{1}\)01] Systeme. Daher ist die aufgelöste Schubspannungskomponente τ _s im (111)/[\(\stackrel{\mathrm{-}}{1}\)01] Schlupfsystem berechnet. Wie in Abb. 7 dargestellt, ist die aufgelöste Schubspannungskomponente τ _s in Richtung M der Gleitebene N kann durch Spannungstensoren berechnet werden durch:

wo a ₁ , b ₁ , c ₁ sind die Richtungskosinus der Normalenrichtung der Ebene N während a ₂ , b ₂ , c ₂ sind die Richtungskosinus der Gleitrichtung M . Während τ _xy , τ _xz , und τ _yz sind die Schubspannungstensoren aus den LAMMPS-Ausgabedaten.

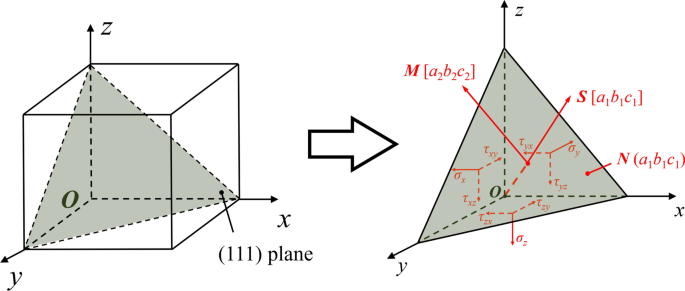
Darstellung der Spannungstensoren

Die Verteilung der aufgelösten Schubspannung τ _s ist in Abb. 8 dargestellt. Die Region mit positivem τ _s ist als Scherbereich definiert, da die Gleitbewegung entlang der [\(\stackrel{\mathrm{-}}{1}\)01]-Richtung gefördert wird, was den Materialabtrag durch Scherung erleichtert. Während die Region mit negativem τ _s wird als Schadensbereich angesehen, da die Gleitbewegung in die entgegengesetzte Richtung bevorzugt wird, was zur Bildung von unterirdischen Schäden im Werkstück führt. In der Extrusionsphase ist die Spannung im Scherbereich geringer als im Schadensbereich. Unter der bearbeiteten Oberfläche können durch Scherverformung verursachte Schäden im Untergrund entstehen [60]. Bei der Bewegung des Schneidwerkzeugs wird die Schubspannung entlang der [\(\stackrel{\mathrm{-}}{1}\)01]-Richtung allmählich erhöht, wodurch der Materialabtragsübergang vom Extrudieren zum Scheren bewirkt wird. Da sich außerdem die Position des Schadensbereichs entlang der Werkzeugbewegung nach oben bewegt, kann der erzeugte Schaden durch weitere Vibrationszyklen entfernt werden und bleibt nicht im Werkstück zurück. Wenn die Temperatur von 300 K auf 1200 K erhöht wird, verringerte sich die Schubspannung im Schadensbereich um 36,1 % bzw. 42,4 % in der Extrusions- und Scherstufe. Im Gegensatz dazu ist aufgrund der Aufwärtsbewegung des Werkzeugs die Abnahme der Schubspannung entlang der [\(\stackrel{\mathrm{-}}{1}\)01]-Richtung im Scherstadium viel weniger offensichtlich. Die kritische aufgelöste Scherspannung (CRSS) für die Gleitbewegung kann ausgedrückt werden als [61]:

wo U und ε repräsentieren die Aktivierungsenergie der Gleitbewegung und die Dehnungsrate. Parameter n und C sind Materialkonstanten. Daraus kann geschlossen werden, dass das CRSS mit steigender Temperatur offensichtlich verringert werden kann. Daher kann die Scherverformung in Richtung [\({\overline{\text{1}}}\)01] bei erhöhter Temperatur erleichtert werden.

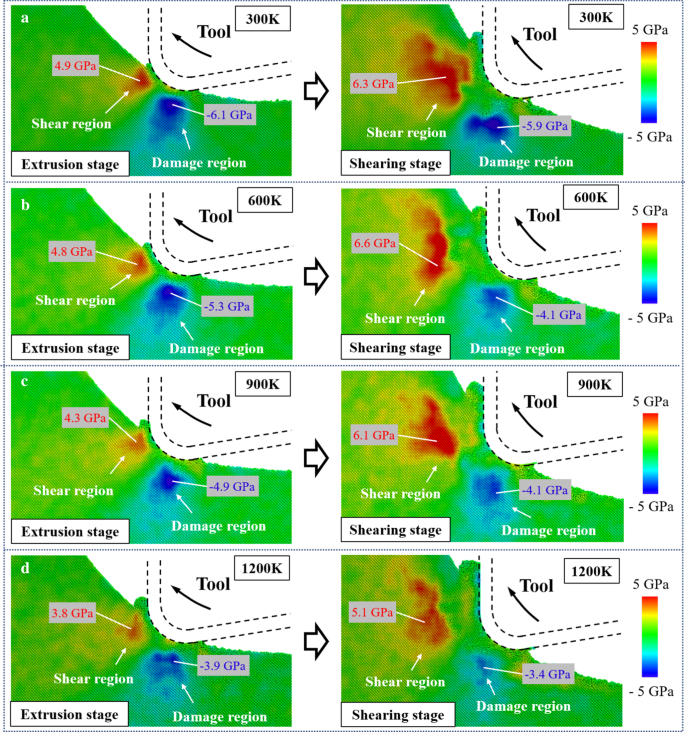
Die aufgelöste Schubspannungsverteilung bei:a 300 K. b 600 K. c 900 K. Tag 1200 K

Phasenübergang

Durch Erhöhung der Schnitttemperatur kann der Phasenübergang von Silizium stark beeinflusst werden. Die Relaxation von a-Si und der Übergang zu Si-I können bei einer geeigneten Temperatur gefördert werden [62]. In Abb. 4 wird das Schadensmuster in den Werkstücken bei hoher Temperatur schmaler. Eine detaillierte Betrachtung des Schadensbildes beim Schneiden bei 1200 K ist in Abb. 9a zu sehen. Es wird beobachtet, dass der erzeugte Schaden im Verformungsbereich nach dem Schneiden teilweise wiederhergestellt wird, was darauf hinweist, dass der Übergang von der Nicht-Diamantstruktur zu Si-I stattgefunden hat. Und mehr Si-I-Atome werden erzeugt, wenn die Schneidtemperatur erhöht wird, wie in Fig. 9b gezeigt. Darüber hinaus ist in Abb. 9c das konstruierte Oberflächennetz (rote Farbe) [63] des bearbeiteten Werkstücks bei 1200 K vorhanden. Es wird beobachtet, dass in dem unter der Oberfläche liegenden Werkstück einige Leerstellen gebildet werden. Da die Atome in der Si-I-Phase dichter gepackt sind, könnte der Übergang zu Si-I eine Schrumpfung des Materials verursachen, was Leerstellen im Werkstück induziert. Das Volumen der Leerstellen bei verschiedenen Temperaturen wird berechnet und ist in Abb. 9d dargestellt. Es wird beobachtet, dass bei Raumtemperatur fast keine Leerstellen erzeugt werden. Während eine deutliche Zunahme der Leerstellen festgestellt werden kann, wenn die Schnitttemperatur auf 900 K und 1200 K erhöht wird.

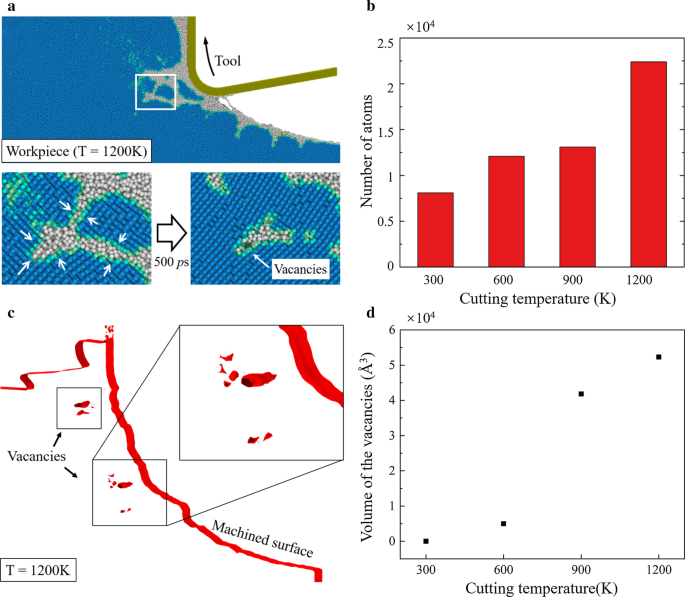
Entspannungsprozess und freie Stellen im Werkstück. a Momentaufnahme des Schadensbildes des Werkstücks bei 1200 K. b Anzahl der Atome, die von der Nicht-Diamant-Struktur in die Si-I-Phase umgewandelt wurden. c Konstruiertes Oberflächennetz des Werkstücks bei 1200 K. d Das Volumen der Leerstellen bei verschiedenen Temperaturen

Eine weitere Analyse der Leerstellen findet sich in Abb. 10. Ein Materialelement unter der bearbeiteten Oberfläche wird ausgewählt, um die Leerstellenerzeugung zu überwachen. Die Anzahl der Atome in der Nicht-Diamant-Struktur und die Spannungsentwicklung des Materialelements sind vorhanden. Daraus wird geschlossen, dass das Materialelement während des Schneidvorgangs zunächst gestaucht wird und dann durch die Aufwärtsbewegung des Werkzeugs auf Zug beansprucht wird. In der Zwischenzeit können bei 300 K zwei Spitzen der Schubspannung beobachtet werden, da die Schubspannung im Schadensbereich beim Passieren des Schneidwerkzeugs erhöht wird. Wenn die Schnitttemperatur erhöht wird, ist die Abnahme der Schubspannung deutlicher als die der Zugspannung. Bei 1200 K ist die zweite Spitze der Schubspannung fast verschwunden, während die Zugspannung während des Relaxationsprozesses im Materialelement dominant wird.

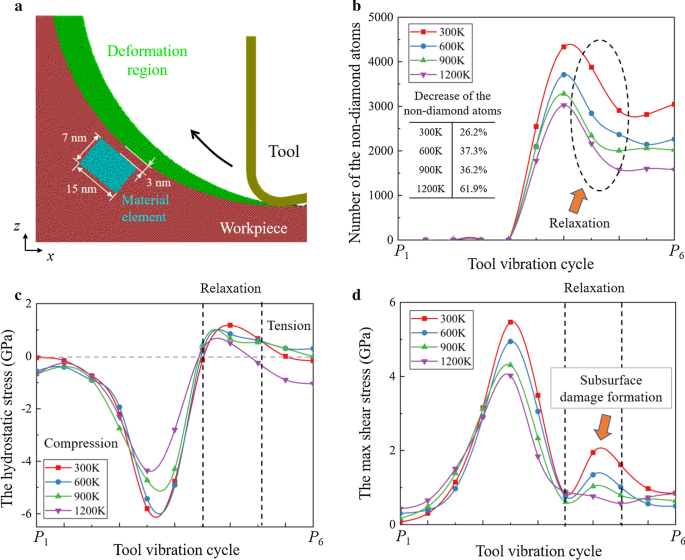
Entspannung während des HM-Prozesses. a Abbildung des materiellen Elements. b Statistik der Atome in Nicht-Diamant-Struktur im materiellen Element. c , d Spannungsverlauf des Materialelements

Um die Wirkung von Zugspannungen auf den Bildungsprozess der Leerstellen zu untersuchen, wurden Relaxationssimulationen von Siliziummassenproben durchgeführt. Wie in Abb. 11a gezeigt, besteht das ursprüngliche Modell aus 40 % Si-I-Atomen und 60 % a-Si-Atomen, das durch die Schmelz-Quench-Methode erzeugt wird [64]. Die Größe des Modells beträgt 21,7 nm × 8,1 nm × 26,1 nm in x , y , und z Richtung, die 230.400 Atome enthält. The initial interface between crystal and non-crystal region is set as (001) crystal plane. Periodic boundary condition is applied in three dimensions to mimic bulk materials. The constructed surface mesh of the relaxed model is present in Fig. 11b. Furthermore, to quantify the vacancies, the solid volume fraction is calculated as the ratio of the solid material volume and the total volume of the simulation sample, as shown in Fig. 11c. It is observed that when temperature is increased, the solid volume fraction decreased obviously under tensile stress. Therefore, to suppress the vacancies, the desired cutting temperature in HM process should be lower than that in ordinary TAC. Meanwhile, the vibration parameters should be optimized to reduce the tensile stress in subsurface workpiece.

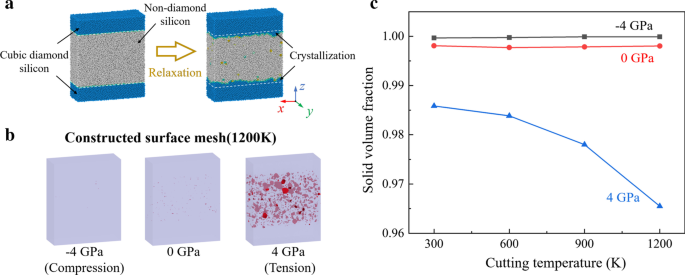
Relaxation simulation of silicon. a Scheme of MD relaxation simulation. b The surface mesh of the relaxed model at 1200 K. c The solid volume fraction curves

Schlussfolgerungen

In this paper, MD simulation is carried out to investigate the cutting mechanism of hybrid machining (HM) process. A modified cutting model is applied to reveal the material removal behavior and subsurface damage formation in one vibration cycle. The main conclusions were as follows:

1. (1)

   During HM process, the dominant material removal mechanism could transform from extrusion to shear in a single vibration cycle. With an increase of the cutting temperature, the generation and propagation of cracks can be effectively suppressed. However, the swelling appears when the dominant material removal mechanism becomes shearing, which is caused by the rotation of the crystal grains in workpiece.

2. (2)

   Based on the stress analysis, the dominant formation mechanism of the subsurface damage in one vibration cycle can be distinct. In the extrusion stage, the subsurface damage can be generated by the shear stress in the damage region. While in the shearing stage, tensile stress becomes dominant in subsurface damage formation. When the cutting temperature is increased, although the tensile stress concentration in the subsurface workpiece is still obvious, the peak value of the stresses is apparently decreased, which effectively suppress the cracks and fractures in workpiece.

3. (3)

   When the cutting temperature is increased, less subsurface damage is generated in the workpiece. However, due to the tensile stress, some vacancies can be generated in the workpiece when the cutting temperature is increased. Therefore, the desired cutting temperature during HM process should be lower than that in ordinary TAC and the vibration parameters should be set carefully to suppress the vacancies in the subsurface workpiece.

Verfügbarkeit von Daten und Materialien

The datasets used and analyzed in the current study can be obtained from the corresponding authors upon reasonable request.

Abkürzungen

TAC:

Thermal assisted cutting

VAC:

Vibration assisted cutting

LVC:

Linear vibration cutting

EVC:

Elliptical vibration cutting

DOC:

Depth of cut

HM:

Hybrid machining

FEM:

Finite-Elemente-Methode

MD:

Molekulardynamik

LAMMPS:

Groß angelegter atomarer/molekularer Massively-Parallel-Simulator

MEAM:

Modified embedded-atom method

SW:

Stillinger–Weber

COMB:

Charge optimized many-body

ABOP:

Analytical bond-order potential

Si-II:

Metallic stable phase

HPPT:

High-pressure phase transition

CNA:

Gemeinsame Nachbaranalyse

a-Si:

Amorphous phase

Si-I:

Single-crystal silicon phase

FCC:

Face Center Cubic

CRSS:

Critical resolved shear stress