Frequenzmodulierte Wellendielektrophorese von Vesikel und Zellen:Periodische Kehrtwendungen bei der Übergangsfrequenz

Hintergrund

Die Polarisierbarkeit eines elektrischen Phänotyps beruht hauptsächlich auf der Zellmembran und den zytoplasmatischen elektrischen Eigenschaften, die von der Frequenz des angelegten elektrischen Feldes abhängen. Dementsprechend können einzelne Zellen durch die Unterschiede in den dielektrischen Spektren unter Verwendung nichtinvasiver elektrischer Techniken identifiziert werden. Die elektrischen Techniken sind derzeit in der Lage, Zellen mit nützlichen Phänotypen aus unbekannten Proben zu trennen [1–15]. Diese bieten gegenüber anderen Trennmethoden den großen Vorteil, dass eine Zellmodifikation durch Antikörper oder eine Adhärenz an Fremdmaterial nicht erforderlich ist, wodurch die Möglichkeit einer Zellschädigung oder Aktivierung durch diese Sonden vermieden wird [1–16]. Die Charakterisierung der zellulären dielektrischen Eigenschaften wurde hauptsächlich unter Verwendung von entweder Impedanzspektroskopie [10, 12, 13] oder Wechselstrom-(AC)-Elektrokinetik wie Dielektrophorese (DEP), Wanderwellen-DEP (twDEP) und Elektrorotation [1, 9, 15]. Unter anderem konzentrieren wir uns auf die Erweiterung der AC-DEP-Methode, um eine neue Methode zur dielektrischen Charakterisierung zu entwickeln, die frequenzmodulierte (FM) Wellen anstelle von Wechselstromfeldern verwendet.

Im Allgemeinen tritt die DEP in einem elektrischen Feldgradienten auf, der eine elektrokinetische Kraft erzeugt, die auf jedes polarisierbare Objekt, geladen oder neutral, in der Richtung ausgeübt wird, die nicht nur durch den Gradientenvektor, sondern auch durch den Realteil des Clausius-Mossotti ( CM) Faktor [1–15, 17–21]. Zum Beispiel betrachten wir die durch das elektrische Wechselfeld induzierte DEP-Kraft E _AC (r ,t ), deren Raum-Zeit-Abhängigkeit als E . ausgedrückt wird _AC (r ,t )=A (r ) cosθ _AC (r ,t ) unter Verwendung des Amplitudenvektors A (r ) und die Phase θ _AC (r ,t ). Die AC-DEP-Kraft wird durch den räumlichen Gradienten der Amplitude erzeugt (d. h. ∇A ) multipliziert mit dem Realteil des CM-Faktors, wie oben erwähnt, während der räumliche Gradient der Phase (d. h. ∇θ _AC ) multipliziert mit dem Imaginärteil des CM-Faktors ergibt die Kraft von entweder twDEP oder Elektrorotation, die daher hinsichtlich der dielektrischen Charakterisierung komplementäre Informationen zur AC-DEP-Methode liefert [9, 15, 20, 21].

In diesem Brief wollen wir die durch ein FM-Feld induzierte DEP-Kraft formulieren und die AC- und FM-DEP-Methoden vergleichen, sodass weder das AC- noch das FM-Feld die räumliche Abhängigkeit der Phase berücksichtigt; daher setzen wir θ _AC (t )=2π f _AC t proportional zur angelegten Frequenz f _AC . Ein wesentliches Merkmal des AC-DEP ist, dass sowohl die Kraftrichtung als auch deren Stärke von f . abhängt _AC . Am bemerkenswertesten ist, dass die Kraftrichtung bei der Übergangsfrequenz f . umgekehrt wird _AC =f _X aufgrund des Vorzeichenwechsels des Realteils des CM-Faktors, der für die dielektrische Charakterisierung mit AC-DEP [1–15] zur Verfügung steht.

Die Frequenzabhängigkeit der AC-DEP-Kraft hat auch folgende Manipulationen ermöglicht [1–15, 22–31]:elektrisch steuerbares Einfangen, Fokussieren und Translation kolloidaler Partikel sowie die Fraktionierung und Charakterisierung von lebenden und/oder tote Zellen. Herkömmliche Systeme für die dielektrophoretische Anordnung und/oder Manipulation kolloidaler Partikel haben oft mikrogefertigte Elektroden verwendet, zwischen denen das elektrische Wechselfeld an kolloidale Suspensionen angelegt wurde, und profitierten von den jüngsten schnellen Fortschritten bei der Herstellung integrierter Halbleiterbauelemente [24-30] . Diese Technologie, die berührungslose Manipulation bietet, wird derzeit in eine Vielzahl von Lab-on-a-Chip-Systemen integriert, die den Vorteil einer genauen und wiederholbaren Handhabung bieten. Dennoch sind die On-Chip-Elektroden, die in Wechselfeldern hochintensive Spots erzeugen, nicht in der Lage, ihre Position unabhängig vom Probenhalter zu verändern, im Gegensatz zum frei positionierbaren Laserfokus bei der optischen Manipulation. Aus der Beschränkung von On-Chip-Systemen folgt, dass die früheren DEP-Verfahren einige Schwierigkeiten und Komplexität bei der Durchführung der Arten von Operationen aufwiesen, für die optische Pinzetten geeignet sind. Ein Kandidatenverfahren zur Überwindung dieser Schwierigkeiten ist die optische bildgesteuerte DEP [32].

Hier haben wir als einfachere Alternative eine der elektronischen Pinzettentechniken [22, 23, 33–38] für die bedarfsgesteuerte dielektrophoretische Montage und/oder Manipulation ohne optisches Gerät gewählt (siehe Abb. 1). Wie aus Fig. 1 ersichtlich ist, verwendet unser Stecksystem ein Paar Mikroelektrodennadeln, die durch Mikromanipulatoren gesteuert werden, um die externen elektrischen Felder in einer kolloidalen Suspension anzulegen. Die Elektrodensonden waren in kolloidalen Suspensionen aufgrund ihrer Steckform nicht feststehend, sondern beweglich. Es bleibt jedoch eine wesentliche Voraussetzung für die praktische Anwendung der dielektrischen Charakterisierung:Die Dauer, während der ein elektrisches Feld an die von salzigen Elektrolyten umgebenen Zellen angelegt wird, sollte minimiert werden. Bei der AC-DEP-Methode werden beispielsweise ineinandergreifende kammartige Elektroden verwendet, die in ein mikrofluidisches System eingebettet sind, so dass Wechselfelder verschiedener Frequenzen gleichzeitig in einer Zellsuspension angelegt werden können [24–30]. Während sich solche verfeinerten On-Chip-Systeme als relevant für die dielektrische Charakterisierung erwiesen haben, ist die Multi-Elektroden-Paar-Technik nicht auf das Ein-Elektroden-Paar-System anwendbar, das oft in der elektronischen Pinzetten-Technik verwendet wird [22, 23, 33–38]. .

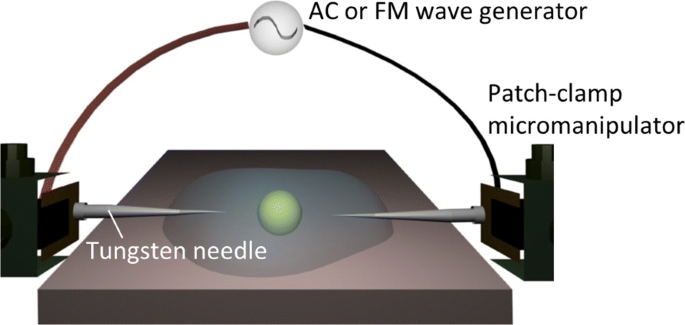
Versuchsaufbau. Ein Schema des dielektrophoretischen Manipulationssystems, das das elektrische Wechselstrom- oder FM-Feld veranschaulicht, das an ein Zielpartikel über ein Paar Elektrodennadeln angelegt wird, die von Patch-Clamp-Mikromanipulatoren gesteuert werden

Um simultane Mehrfrequenzmessungen mit dem Ein-Elektroden-Paar-System (Abb. 1) durchzuführen, sollte die Änderung des angelegten elektrischen Feldes untersucht werden. In diesem Schreiben sprechen wir die Verfügbarkeit von zeitvariabler DEP aufgrund einer FM-Welle (FM-DEP) der folgenden Form an:

wobei die Phase θ (t ) der FM-Welle bezieht sich auf die Momentanfrequenz f (t ) als 2π f (t )=d θ (t )/d t und

mit f _m bezeichnet die Modulationsfrequenz. Wir verwenden das Breitband-FM, das erfüllt, dass Δ f /f _m ≫1, so dass die Bedingungen von f _m /f (t ), f _m /f _c , f _m /Δ f ≪1 wird in der unten angegebenen theoretischen Formulierung als Breitbandgrenze (WBL) bezeichnet.

In diesem Brief wird besonderes Augenmerk auf den Zusammenhang zwischen der charakteristischen Frequenz von f _X und die Flugbahn von FM-DEP. Im nächsten Abschnitt beschreiben wir sowohl die verwendeten Materialien als auch Details des Plug-in-Systems zur Induktion von FM-DEP. Der dritte Abschnitt enthält die Ergebnisse und die Diskussion, die aus vier Teilen besteht. Zuerst untersuchen wir die Details der sich wiederholenden Kehrtwendungen einer einzelnen Leukämiezelle, indem wir die reziproke Flugbahn quantifizieren, deren Periodizität durch die Modulationsfrequenz f . erklärt wird _m , oder die periodische Schwingung von f (t ) gegeben durch Gl. (2). Als nächstes erklären wir die reziproke Trajektorie theoretisch, indem wir die zeitvariable dielektrophoretische Kraft herleiten, die gemäß der Momentanfrequenz f . moduliert (t ) des FM-Feldes, das die WBL-Bedingung erfüllt. Die erhaltene Form der dielektrophoretischen Kraft liefert die Gleichung, die die f . bestimmt _X aus den beobachteten Kehren. Drittens messen wir die Größe der dielektrophoretischen Kraft auf ein multilamellares Vesikel (MLV), das aufgrund der Anziehung des AC-DEP an einer Elektrodennadel befestigt war. Die Frequenzabhängigkeit der Kraft wurde mit der aus dem Realteil des CM-Faktors ermittelten Spektralgleichung angepasst, sodass f _X wurde als die charakteristische Frequenz bestimmt, bei der die Anziehungskraft aufgrund von AC-DEP verschwindet. Da die FM-DEP-Methode auch f . liefert _X Durch die Analyse der reziproken Trajektorie eines MLV beurteilen wir das Ausmaß der Koinzidenz zwischen den von AC- und FM-DEPs bewerteten Übergangsfrequenzen. Schließlich wurden sowohl die zytoplasmatischen Leitfähigkeiten als auch die Membrankapazitäten von drei Zellarten anhand von f . bewertet _X als ansteigende Funktion der Leitfähigkeit der Lösung, und die erhaltenen Werte wurden mit den in der Literatur angegebenen verglichen.

Methoden

Materialien

Zur Herstellung multilamellarer Vesikel (MLVs) verwendeten wir 1,2-Dioleoyl-sn-glycero-3-phosphatidylcholin (DOPC) als Lipide, bezogen von Avanti Polar Lipids. Die MLVs wurden durch das folgende Verfahren erhalten. Das DOPC (1 ml, 20 mM) gelöst in Chloroform/Methanol (2:1 v /v ) wurde mit N₂ . getrocknet Gas, und das Lösungsmittel wurde mehr als 12 h im Vakuum vollständig entfernt. Der durch die Verdunstung auf dem Glasfläschchen abgeschiedene dünne Film wurde mit entionisiertem Wasser rehydratisiert und mehrere Stunden bei 25 °C inkubiert.

Zwei in den Experimenten verwendete Zelllinien waren JKT-beta-del der menschlichen T-Zell-Leukämie (TL)-Linie und CCRF-SB der menschlichen B-Zell-Leukämie (BL)-Linie. Beide Arten von TL- und BL-Zellen wurden nach 1-wöchiger Inkubation in einem befeuchteten Inkubator verwendet, der 5 % . enthält CO₂ bei 37, so dass wir die Zellkonzentrationen im Bereich von 0,5×10 ⁶ . hatten bis 1×10 ⁶ Zellen/ml. Das RPMI 1640-Medium für die Zellkultur wurde mit 10 % fötalem Brovinserum und 100 mM Natriumpyruvat ergänzt. Die Zellen wurden durch Zentrifugation bei 370g . sedimentiert für 3 min zweimal, damit die Zellen vor dem Pipettieren in 1 ml des RPMI 1640 Mediums rein resuspendiert werden konnten. Die erhaltenen Zellsuspensionen wurden unter Verwendung der isotonischen 200 mM Saccharoselösung weiter verdünnt, um das Lösungsmittel mit der erforderlichen Leitfähigkeit vorzubereiten

Wir haben auch menschliche rote Blutkörperchen (RB) verwendet, die in den folgenden Suspensionen dispergiert waren. Frisch entnommene Vollblutproben wurden von gesunden Freiwilligen Anfang Zwanzig erhalten. Die Zellen, suspendiert in einer Mischung aus RPMI 1640-Medium und 3,1% Hämatokrit, wurden unter Verwendung der isotonischen 200 mM Saccharoselösung verdünnt, um das Lösungsmittel mit der erforderlichen Leitfähigkeit sowie die obigen Leukämiezellen vorzubereiten. Alle dielektrophoretischen Experimente mit den menschlichen RB-Zellen wurden innerhalb von 10 Minuten nach der Entnahme der Vollblutproben abgeschlossen.

Experimentelle Einrichtung

Die Leitfähigkeiten der Zellsuspensionen wurden mit einem Leitfähigkeitsmeßgerät (SevenMulti, Mettler-Toledo, Columbus, OH, USA) gemessen. Eine schematische Darstellung des verwendeten Stecksystems ist in Abb. 1 dargestellt. Ein externes elektrisches Feld mit einer AC- oder FM-Welle wurde über einen Arbitrary Waveform Generator (Agilent 33220A, Agilent Technologies, Santa Clara, CA, USA) mit einem Strom angelegt Verstärker (F30PV, FLC Electronics, Partille, Schweden), an den steckbare Mikroelektroden angeschlossen wurden. Die Mikroelektroden bestanden aus Wolframnadeln mit einem Spitzendurchmesser von 0,5 μ m, die unabhängig von zwei Sätzen von Patch-Clamp-Mikromanipulatoren (NMN-21, Narishige, Setagaya-ku, Tokio, Japan) gesteuert wurden. In allen folgenden Experimenten haben wir den Spitzenabstand bei 100 μ . gehalten m beim Anlegen der externen Felder an die obigen Suspensionen, und die maximale Stärke wurde auf 0,5 kV/cm eingestellt. Das Nadelpaar wurde in einen Probentropfen eingeführt, der an einem inversen optischen Mikroskop (TE2000-U, Nikon, Minato-ku, Tokio, Japan) angebracht war, und die lichtmikroskopischen Aufnahmen wurden unter Verwendung einer CCD-Kamera (Retiga Exi, QImaging, Surrey, British) aufgenommen Columbia, Kanada) mit einer Bildrate von 25 fps; übrigens wurde bestätigt, dass die Frequenzauflösung von FM-Wellen aufgrund der Bildfrequenz immer innerhalb der Fehlerbalken für alle Daten lag. A 50- μ Ein Tropfen Suspension wurde auf den Probentisch des inversen optischen Mikroskops aufgebracht, dessen Temperatur mit einem Wärmeregler auf 25 °C gehalten wurde.

Die Stecktechnik ermöglicht es dem einfachen System, verschiedene berührungslose Manipulationen an einer einzelnen Zelle vorzunehmen, beispielsweise diese berührungslos in einen engen Kanal zu schieben und in die gewünschte Richtung auszurichten. Obwohl es oft notwendig ist, die Zellen in einer isotonischen Lösung mit Salz zu behandeln, ist es am einfachsten, die obigen DEP-Manipulationen von Zellen durchzuführen, die von entionisiertem Wasser umgeben sind. In Zusatzdatei 1:Filme S1 bis S3 induzierte das Plug-in-System die AC-DEP von Diatomeenzellen, die in entionisiertem Wasser suspendiert waren. Aus Zusatzdatei 1:Filme S1 bis S3 können wir sehen, dass eine in salzfreiem Wasser dispergierte anisotrope Diatomeenzelle wie ein Post-it-Tag durch ein Paar Mikroelektroden manipuliert wurde, zwischen denen das elektrische Wechselfeld (1 kV/cm) angelegt wurde . Die berührungslosen Operationen bestehen aus drei Schritten:(i) Eine Zielzelle wurde zuerst parallel zu einer positiv geladenen Glaswand durch die Kombination von Dipolausrichtung bei einer Frequenz von 30 kHz und Positionsänderung jeder Mikroelektrode gedreht (Zusatzdatei 1:Film S1 ), (ii) haben wir anschließend die Frequenz auf 100 kHz geändert, um sie gegen die Wand zu drücken, um die Anfragezelle mit negativen Ladungen auf der Glasoberfläche elektrostatisch zu fixieren (Zusatzdatei 1:Film S2), und (iii) die AC-Frequenz wurde angepasst auf 20 MHz, um die AC-DEP in die entgegengesetzte Richtung zu induzieren, damit die elektrostatisch befestigte Zelle herausgezogen werden kann (Zusatzdatei 1:Film S3).

Ergebnisse und Diskussion

Experimentelle Beobachtung einer Leukämiezelle mit FM-DEP

Unsere steckbaren Mikroelektroden (siehe Abb. 1) ermöglichen das Anlegen des elektrischen Feldes an die weit über dem Probensubstrat schwebenden Partikel, was für die Auswahl geeigneter Zellen praktisch nützlich ist. Zum Beispiel zeigt zusätzliche Datei 1:Film S4, dass das Mikroelektrodenpaar so gesteuert wurde, dass es sich einer schwimmenden dreieckigen Diatomeenzelle nähert, an die wir das elektrische Wechselfeld mit seiner Frequenzsprung zwischen 100 und 500 kHz in Intervallen von 0,5 s angelegt haben. In Zusatzdatei 1:Film S4 sehen wir die dreieckige Zelle, die aufgrund des Frequenzsprungs auf einer Mikroelektrode aufprallt, als vorläufiges Ergebnis vor der folgenden Manipulation mit dem FM-DEP.

Zusätzliche Datei 1:Die Filme S5 und S6 zeigen typische Verhaltensweisen mehrerer TL-Zellen, die die FM-DEP erfahren, die denen von Säugerzellen ähneln, die mit einer elektronischen Pinzette unter Verwendung einer einzelnen Elektrode AC-DEP manipuliert werden [36]. Abbildung 2 zeigt eine der periodischen Trajektorien unter Verwendung des 3D-Plots von (x ,y ) entlang der t Achse, wobei eine relative Koordinate von (x ,y ) wird der temporären Zellposition zugeordnet, wobei der Ursprung von (0, 0) an einem bestimmten Punkt auf einer Mikroelektrodennadel zum Extrahieren der Zell-Elektroden-Konfiguration liegt. Während das x Achse stellt die Tangente an die Elektrodenoberfläche bei (0, 0) dar, die y Achse, senkrecht zur Tangente, spiegelt hauptsächlich die Projektion der nachfolgend erläuterten periodischen Kehrtwendungen wider. In Abb. 2 haben wir eine schwimmende TL-Zelle ausgewählt, an die wir das elektrische FM-Feld mit seiner Modulationsfrequenz f . angelegt haben _m eingestellt auf f _m =0,25 Hz im Bereich von 200 kHz ≤f (t )≤ 3 MHz. Weil wir das haben Δ f /f _m , f (t )/f _m <10 ⁻⁵ , gilt die WBL-Bedingung tatsächlich, wie nach Gl. (2).

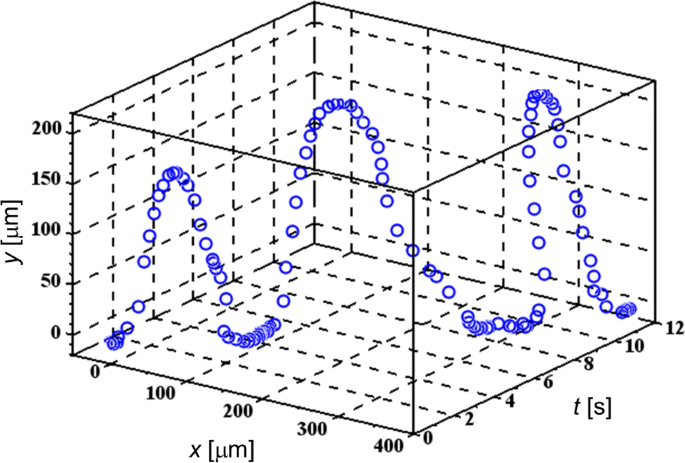
3D-Trajektorie einer gezielten TL-Zelle. Periodische Kehrtwendungen aufgrund der Frequenzmodulation werden für die TL-Zelle demonstriert, die der FM-DEP unterzogen wird

Aus Zusatzdatei 1:Filme S5 und S6 sowie Fig. 2 ist ersichtlich, dass die periodische Flugbahn aus drei Teilen des Verlassens, Annäherns und Verbleibens auf der Mikroelektrode besteht:(i) die Zelle verlässt die Mikroelektrode, (ii) es nähert sich der Mikroelektrode, nachdem es eine Kehrtwende gemacht hat, und (iii) es bleibt auf der Mikroelektrodenoberfläche. Die Zelle kann aufgrund des Lösungsmittelflusses oft nicht in die gleiche Position auf der Mikroelektrodenoberfläche zurückkehren, was nicht nur in Zusatzdatei 1:Film S6 zu beobachten ist, sondern auch durch die U-Turns mit der in die <. wandernden Zelle dargestellt wird i>x Richtung in Abb. 2. Trotz der Störung des Lösungsmittelflusses ist es möglich, die Momente zu unterscheiden, in denen die Zelle die Mikroelektrodenoberfläche verlässt bzw. die Kehrtwende in der periodischen Bahn durchführt. Dementsprechend können wir aus Abb. 2 sehen, dass diese Kehrtwendungen in Abständen von 4 s in Übereinstimmung mit der Modulationsfrequenz von 0,25 Hz oder der 4-s-Periode der Momentanfrequenz f . wiederholt werden (t ).

Theoretische Studie zum FM-DEP

Um die experimentellen Trajektorien, einschließlich der periodischen Kehrtwendungen, zu erklären, betrachten wir ein kugelförmiges Objekt als vereinfachtes Modell einer einzelnen Zelle, auf die ein beliebiges zeitvariables elektrisches Feld E (r ,t ) wird angewandt. Abbildung 3 zeigt schematisch die zeitabhängige DEP-Kraft, die auf ein kugelförmiges Objekt einwirkt [9]. Wie in Abb. 3 gezeigt, werden die Permittivität und die Leitfähigkeit innerhalb eines kugelförmigen Objekts durch ε . dargestellt _in und σ _in , und das tiefgestellte „out“, wie zum Beispiel ε _aus und σ _aus , bezeichnet das Äußere. Im Allgemeinen F _DEP (r ,t ) steht im Zusammenhang mit dem induzierten Dipolmoment p (r ,t ) als [17–19]

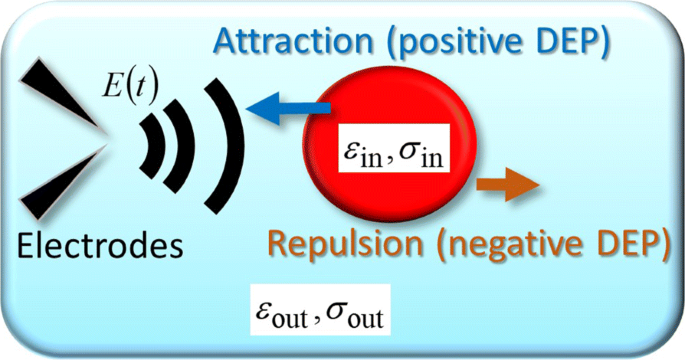
Theoretisches Modell. Schematische Darstellung der FM-DEP-Kraft, die auf eine Zelle ausgeübt wird, die als homogenes Kugelmodell mit der Permittivität und Leitfähigkeit von ε . modelliert wird _in und σ _in , bzw. Die Kugel ist von einem Elektrolytmedium mit einer Permittivität und Leitfähigkeit von ε . umgeben _aus und σ _aus , bzw. Das homogene Kugelmodell ist die Vereinfachung des kugelförmigen Einschalenmodells, das die Zelle als ausgeschmiertes Zytoplasma, umgeben von einer Membran, betrachtet [9]

wo K _H und Δ τ sind wie folgt definiert:K _H =(ε _in −ε _aus )/(ε _in +2ε _aus ), und \(\Delta\tau^{-1}=\tau_{0}^{-1}-\tau^{-1}\) mit dem Radius R des kugelförmigen Objekts und zwei charakteristische Zeiten von τ ₀ =(ε _in −ε _aus )/(σ _in −σ _aus ) und τ =(ε _in +2ε _aus )/(σ _in +2σ _aus ).

Ersetzen des elektrischen Wechselfeldes E _AC (r ,t )=A (r ) cos(2π f _AC t ) in Gl. (3) bis (5) erhalten wir die mittlere DEP-Kraft <F _DEP (r ,t )> die über Zyklen des Wechselfeldes gemittelt wurde [9, 15, 20]:

wo A _RMS bezeichnet den quadratischen Mittelwert (RMS)-Vektor, der erfüllt, dass \(\boldsymbol {A}_{\text {RMS}}^{2}=\boldsymbol {A}^{2}/2\), und χ (f _AC )≡2π R ³ ε _aus Re[K (f _AC )] hängt von der angelegten Frequenz ab f _AC wegen Re[K (f _AC )], der Realteil des CM-Faktors [9, 15, 20]:

wo K _L =(σ _in −σ _aus )/(σ _in +2σ _aus ) und K _H , oben definiert, entsprechen den realen CM-Werten in den Nieder- bzw. Hochfrequenzgrenzen, und diese Grenzwerte, K _L und K _H , müssen entgegengesetzte Vorzeichen haben, damit f _X definiert durch χ (f _X )=0 kann existieren [9, 15, 20].

Gleichungen (6) und (7) zeigen, dass das elektrische Wechselfeld die DEP-Kraft erzeugt, deren Richtung von der angelegten Frequenz abhängt f _AC bis χ (f _AC ) gegeben durch Gl. (7), die die hüpfende Diatomeenzelle in Zusatzdatei 1:Film S4 wie folgt erklärt (siehe auch Abb. 3). Wenn die angelegte Frequenz das Pluszeichen des Realteils des CM-Faktors liefert (d. h. χ (f _AC )>0), können wir Zellen beobachten, die von den Elektrodennadelspitzen (der positiven DEP) angezogen werden, an denen die Stärke des AC-Feldes, das über ein Paar Elektrodennadeln angelegt wird, am größten ist. Das Vorzeichen des reellen CM-Faktors kann bei f . ins Negative umgekehrt werden _X , die verschwindende Frequenz des realen CM-Faktors (d. h. χ (f _X )=0), wobei wir die dielektrophoretische Kraft Null haben, wie sie aus Gl. (6). Im negativen Vorzeichen des CM-Faktors (d. h. χ (f _AC )<0), werden einzelne Kolloide vom Elektrodennadelpaar abgestoßen (das negative DEP). Die dreieckige Diatomeenzelle in Zusatzdatei 1:Film S2 prallte aufgrund der entgegengesetzten Richtung der AC-DEPs ab, die durch die AC-Felder mit ihren Frequenzen von 100 und 500 kHz induzierten; Kombinieren von Gl. (6) und den beobachteten dielektrophoretischen Richtungen finden wir, dass χ (100 kHz)>0 und χ (500 kHz)<0.

Als nächstes betrachten wir die FM-DEP, indem wir die durch Gl. (1) und (2) in Gl. (3) bis (5). Wie in Zusatzdatei 2 bewiesen, bestätigt die WBL-Bedingung der FM-Welle die angenäherte Form der Integration in Gl. (5), wodurch

die die gleiche Form wie die des AC-DEP annimmt, wenn die zeitabhängige Frequenz f (t ) wird durch eine konstante Frequenz von f . ersetzt _AC . Damit erhalten wir die Grenzform der mittleren DEP-Kraft <F _DEP (r ,t )> der über Zyklen von θ . gemittelt wurde (t ) im FM-Feld (siehe Gl. (A1), (A13) und (A14) in Zusatzdatei 2):

eine ähnliche Form wie Gl. (6) für die AC-DEP. Der Unterschied besteht darin, ob der Koeffizient von χ {f (t )} hängt von t . ab bis f (t ), die sich zyklisch entsprechend der Frequenzmodulation mit der Periode von T . ändert _m =1/f _m .

Basierend auf dem einfachen Ausdruck (9) der FM-DEP veranschaulichen wir mit Fig. 4 den Mechanismus der obigen Kehrtwendungen aufgrund der FM-Welle. Abbildung 4 zeigt eine schematische Darstellung der durch die FM-Welle in der WBL induzierten DEP, wenn der Bereich von f (t ) deckt die Übergangsfrequenz f . ab _X so dass f _c −Δ f ≤f _X ≤f _c +Δ f . In Abb. 4 wird angenommen, dass die Frequenzabhängigkeit des Realteils des CM-Faktors, oder χ {f (t )}, liefert die alternativen Vorzeichenänderungen wie folgt:Minuszeichen (χ {f (t )}<0) für f (t )<f _X und Pluszeichen (χ {f (t )}>0) für f (t )>f _X , was bei unseren Experimenten der Fall ist. Die frühere Periode erfüllt f (t )<f _X hat eine Dauer, während letztere f (t )>f _X während der restlichen Periode beibehalten wurde:Ein Zyklus wird in zwei Perioden unterteilt, die in Abb. 4 rot bzw. blau markiert sind.

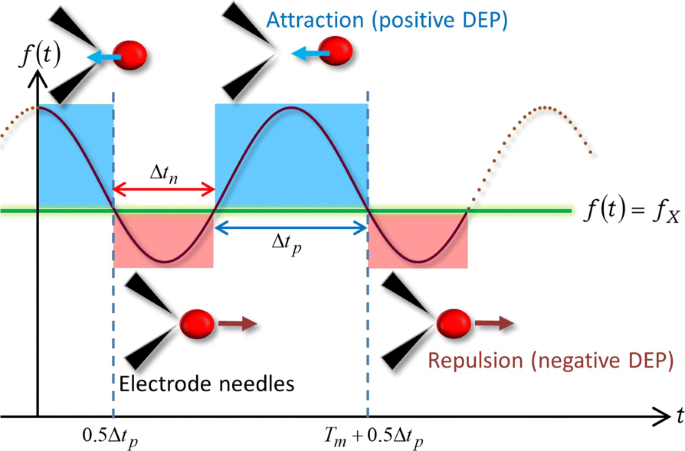
Kraftrichtung bezogen auf die Frequenzmodulation. Eine Illustration der periodischen Kehrtwendungen aufgrund der FM-Welle mit ihrer zeitabhängigen Frequenz von f (t ) für eine Übergangsfrequenz f _X

Ähnlich wie bei AC-DEP, Gl. (9) impliziert, dass das Minuszeichen (χ {f (t )}<0) erzeugt eine abstoßende DEP-Kraft zwischen der Zelle und den Mikroelektroden, während gleichzeitig erfüllt wird, dass f (t )<f _X . Als Ergebnis verlässt die Zelle den Bereich um die Mikroelektrodennadelspitzen, zwischen dem die Stärke des elektrischen Feldes am größten ist:Die Zelle erfährt die negative DEP während der roten Periode von Δ t _n in Abb. 4. Im Moment t _X als Lösung von f (t _X )=f _X , χ (f ) verschwindet, gefolgt vom Vorzeichenwechsel in χ (f )>0 während f (t )>f _X , und entsprechend wird die DEP-Kraft bei t . auf die Anziehungskraft umgestellt _X . Nach einer Kehrtwende bei t _X Aufgrund der Richtungsumkehr der DEP-Kraft beginnt die Zielzelle, sich der Mikroelektrode zu nähern, wandert in die entgegengesetzte Richtung und wird schließlich zwischen den Spitzen der Elektrodennadeln gefangen oder an einer der Elektroden befestigt:Die Zelle erfährt die positive DEP während die blaue Periode von Δ t _p in Abb. 4. Abb. 4 zeigt, dass der Zyklus des Verlassens, Annäherns und Verbleibens auf der Mikroelektrode mit der Modulationsperiode von T . wiederholt werden sollte _m , in Übereinstimmung mit Abb. 2:Δ t _n +Δ t _p =T _m . Der in Abb. 4 dargestellte dielektrophoretische Mechanismus kann somit die periodischen Kehrtwendungen erklären, die in Zusatzdatei 1:Filme S5 und S6 sowie in Abb. 2 beobachtet wurden.

Betrachten wir die periodische Lösung der Gleichung f (t _X )=f _X . Wie aus Abb. 4 ersichtlich, t _X wird ausgedrückt als t _X =n T _m +0,5Δ t _p =n T _m +0,5(T _m −Δ t _n ) mit einer ganzen Zahl von n =0, ±1, ±2,⋯, was weiter lautet

Ersetzen von Gl. (10) in Gl. (2) haben wir für n =0 dass

Klarstellung, dass die FM-DEP-Methode die Übergangsfrequenz bestimmt, wenn die Dauer Δ t _n from leaving the microelectrode to doing the U-turn can be measured precisely.

Comparing Crossover Frequencies of a Single MLV Determined from the FM- and AC-DEPs

We investigated the experimental accuracy of Eq. (11). Experimentally, it is often necessary for the biological cells to be dispersed in an electrolyte. For MLVs, however, the use of deionized water is allowed during the preparation process of rehydration and dilution. We thus used the salt-free MLV suspension for comparing the crossover frequencies determined from both AC- and FM-DEPs.

The dielectrophoretic U-turns of a targeted MLV were induced by the FM wave in the range of 10 kHz ≤f (t )≤ 50 kHz (i.e., f _c =30 kHz and Δ f =20 kHz) with a setting that f _m =0.1 Hz, and correspondingly the FM-DEP has a 10-s period. In the experiments, it takes less than 30 s to observe a few U-turns of the targeted MLV from leaving to approaching microelectrodes. From the trajectory, we obtained the mean leaving time that \(\overline {\Delta t_{n}}=5.8\pm 0.2\) s. Because the WBL condition applies to the present experiment satisfying that f _m /Δ f /f _m , f _, m /f (t )<10 ⁻⁵ , the crossover frequency was evaluated to be f _X =35±1 kHz from substituting \(\overline {\Delta t_{n}}=5.8\pm 0.2\) s into Eq. (11).

For comparison, we made use of the programmable manipulator in the AC-DEP method that tries to evaluate the crossover frequency of the same targeted MLV to which the sinusoidal electric field with a frequency in the range of 30 to 100 kHz was applied via the electrode needle pair for inducing the AC-DEP. Because the programmable manipulator carries the electrode needle pair at a constant speed in one direction, we can measure the dielectrophoretic force similarly to the laser-trapping experiments [39]. Attaching the MLV on an electrode tip that undergoes uniform linear motion, not only the AC-DEP force but also the hydrodynamic force caused by the one-dimensional motion are exerted on the MLV. With the gradual increase of electrode velocity, F _DEP eventually becomes smaller than the hydrodynamic force. As a result, the MLV initially attached to the moving electrode, owing to the DEP attraction, is desorbed by the hydrodynamic force. Defining the critical value, v _c , by the maximum velocity value of the microelectrode pair prior to the desorption, the force balance equation between the DEP and hydrodynamic forces reads [39]

where F _DEP (f _AC )e ≡<F _DEP> with the unit vector e defined by \(\boldsymbol {e}=\nabla {\boldsymbol {A}}^{2}_{\text {RMS}}/|\nabla {\boldsymbol {A}}^{2}_{\text {RMS}}|\), η the water viscosity at 25 °C and 2R the diameter of the MLV.

Additional file 1:Movies S7 and S8 demonstrates the force measurement using the above AC-DEP method at the applied frequency of f _AC =60 kHz. In Additional file 1:Movie S7, the velocity of the electrode pair controlled by the programmed manipulator is 110 μ m/s, which is lower than v _c ; therefore, the MLV remains attached to one part of the electrode pair owing to the dielectrophoretic attraction. Additional file 1:Movie S8, on the other hand, shows the higher electrode speed of 120 μ m/s, under which the dielectrophoretic force becomes smaller than the hydrodynamic force that is exerted on the MLV, thereby desorbing the MLV from the electrode. Accordingly, v _c is evaluated to be 110 μ m/s ≤v _c ≤ 120 μ m/s, and we can calculate F _DEP (60 kHz) using Eq. (12).

We can determine f _X from the experimental results of F _DEP at various external frequencies. Figure 5 shows the frequency dependence of F _DEP , indicating that the DEP force experienced by the MLVs was reduced by lowering the applied frequency. It is found from Eqs. (6) and (7) that the fitting function of F _DEP (f _AC ) can be expressed as

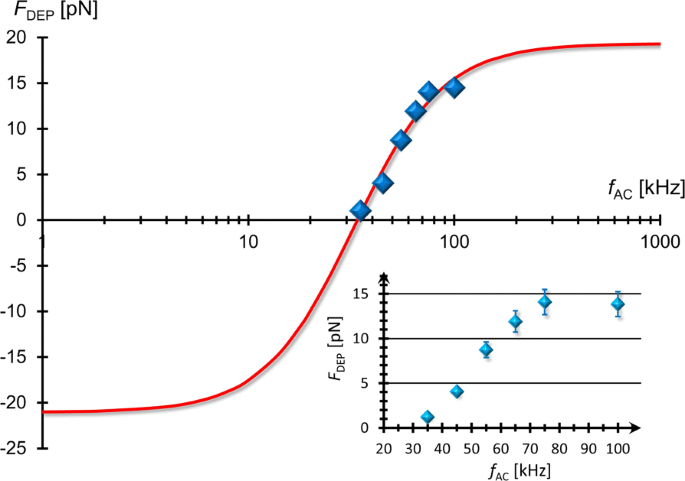
Frequency dependence of F _DEP . The FM-DEP force (F _DEP ) as a function of external frequency (f _AC ) of applied AC field where F _DEP has been evaluated from Eq. (12), the balance equation between the FM-DEP and hydrodynamic forces exerted on a single MLV. It can be seen that F _DEP is increased and saturated as f _AC is higher, reflecting a typical behavior of the relaxation spectrum of the real CM factor. The solid line represents the best-fit result of Eq. (13)

implying that

Equation (13) is depicted by the solid line in Fig. 5 that has been fitted to the experimental data using the best-fit results of three parameters:L =−21.02 pN, H =19.03 pN, and τ =4.9 μ S. Substituting these results into Eq. (14), we evaluate that f _X =34.15 kHz, which coincides with the result of f _X =35±1 kHz evaluated from the FM-DEP method. The FM-DEP method is thus validated in terms of the consistency with the direct force measurement using the AC-DEP method.

Conductivity Dependencies of the Crossover Frequencies for Biological Cells

Let us return to the dielectrophoretic U-turns of biological cells mentioned in Fig. 2 to assess the practical reliability of the crossover frequencies when the FM-DEP method is applied to cell suspensions. Recently, an elaborate theory [40] has investigated, in more detail than before, the relationship between the homogeneous sphere model (see Fig. 3) and the single-shell model where the inner structure of cell is represented by a smeared-out cytoplasm surrounded by a membrane. As a result, the relation between f _X and the suspension conductivity σ _out has been formulated using radius R of a cell, membrane capacitance C _m , and cytoplasmic conductivity σ _cyt [40]:

where f _{X 0} is the extrapolated value to the crossover frequency at σ =0 mS/m and will be treated as a fitting parameter herein. The elaborate treatment adds the squared term, the second term on the right hand side of Eq. (15), to the conventional linear relation which has mainly been used for evaluating C _m from f _X [40–45]. Theoretically, it has still been claimed [40] that Eq. (15) is valid within a lower range of σ _out such that σ _out <10 mS/m; however, it should be better to include the squared term in the evaluation of C _m , considering that our range of σ _out is relatively high compared with previous results in the range of 10 mS/m ≤σ _out ≤ 100 mS/m [40–45]. Hence, we determined σ _cyt as well as C _m from fitting Eq. (15) to the experimental results of f _X as an increasing function of σ _out .

There are three kinds of biological cell used:TL and BL cells of human leukemia and RB cells of three human volunteers. In all the experiments using any species of cell, the conductivities were within the range of 60 to 160 mS/m, and the modulation frequency was set to be 0.25 Hz. Regarding the instantaneous frequency, most of the experiments adopted the range from 100 to 1.5 MHz (i.e., f _c =800 kHz and Δ f =700 kHz); exceptionally for leukemia cells, the frequency range was extended to 50 kHz ≤f (t )≤1550 kHz (i.e., f _c =800 kHz and Δ f X =750 kHz) in the conductivity range of 60 mS/m≤σ ≤80 mS/cm because f _X in this σ -range has been found to be lower than 100 kHz, and we were unable to observe the DEP U-turns in the range of 100 kHz ≤f (t )≤1500 kHz. Both of these frequency sets satisfy the WBL condition of Δ f /f _m , f (t )/f _m <10 ⁻⁵ as before.

Each time we measured the leaving times of cells dispersed in a suspension, we looked for an appropriate spot at which a few cells having a similar size could simultaneously experience the FM-DEP above the substrate, and the microelectrode tips were placed at the measurable position using the micromanipulator. We continued such scanning inside the cell suspensions until the FM-DEP trajectories of 10 cells were collected in total at a couple of appropriate positions. For each kind of cell, the measurement of 10 cells was repeated twice using different drops of the same cell suspension. As mentioned, it is indispensable for the implementation of the FM-DEP measurement at each spot to suppress the electrically induced solvent flows as much as possible. Hence, we traced only two cycles of the U-turn path so that the duration time of applying the electric field could be adjusted to be less than 10 s, and, correspondingly, the leaving time of each cell is given as the average of each trajectory, including the two U-turns. The mean leaving time \(\overline {\Delta t_{n}}\) of each cell suspension is thus obtained from averaging the leaving times of 20 cells. Particularly for human RB cells, we further averaged three sets of the mean crossover frequencies obtained for three RB cell suspensions of three human beings, supposing that cells of the same species are similar in C _m and σ _cyt as well as in R . The two-step averaging of Δ t _n will be denoted by \(\left <\overline {\Delta t_{n}}\right>\). Substituting into Eq. (10) the experimental data of either \(\overline {\Delta t_{n}}\) or \(\left <\overline {\Delta t_{n}}\right>\), the mean crossover frequency <f _X > was obtained.

Figure 6 shows the σ _out -dependencies of <f _X > measured for the above three kinds of biological cells using the FM-DEP method. The solid lines in Fig. 6 depict the best-fit results of Eq. (15). We evaluated C _m and σ _cyt from the best fitting of Eq. (15) into which the observed radii (R _obs ) were inserted. Table 1 lists the fitting results of C _m and σ _cyt , where we used the observed radii of 10 μ m ≤ 2R _obs ≤ 15 μ m for TL and BL cells, and 7.5 μ m ≤ 2R _obs ≤ 10 μ m for RB cells in evaluating C _m . It is to be noted from Table 1 that different species have different membrane capacitances, which are in good agreement with those reported in the literature [40–47]; the C _m values of RB cells with stationary whole blood samples from normal (healthy) donors are in excellent agreement with our value [46, 47], but are substantially higher than those of washed RB cells in isotonic buffered saline as noted in [47]. The best-fit results simultaneously provided cytoplasmic conductivities, which were consistently similar as seen from Table 1, but were slightly lower than the range of previous reports that 0.2 S/m ≤σ _cyt ≤1 S/m [40, 45, 48–51]. These results support that the FM-DEP method retains the practical reliability needed for the treatment of living cells.

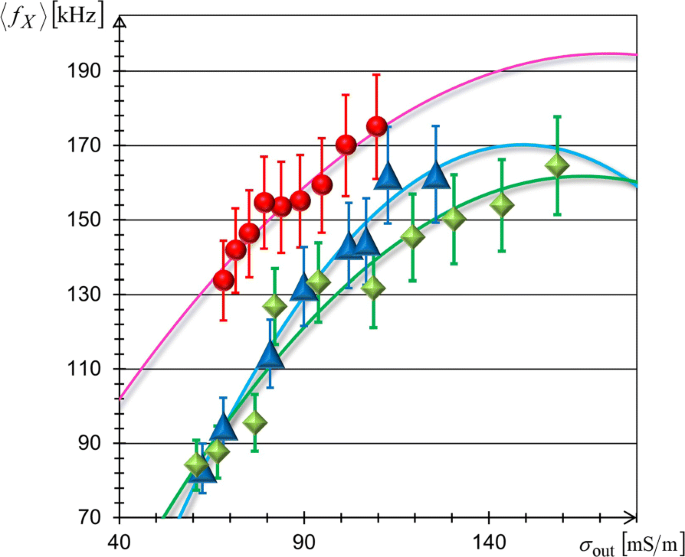
Conductivity dependences of crossover frequencies. Mean crossover frequency, <f _X >, of TL cells (blue triangles), BL cells (green diamonds), and RB cells (red circles) varying with increase of solution conductivity σ _out . The best-fit results of Eq. (15) are delineated by the solid lines

Schlussfolgerungen

Our theoretical treatment of the FM-DEP has mainly focused on the WBL condition. In this limit, we have proved theoretically that the direction of the FM-DEP force switches each time when the instantaneous frequency of the FM wave traverses the crossover frequency, thereby implying the periodic U-turns of micro/nanoparticles that undergo the FM-DEP. Two kinds of experiment have demonstrated the accuracy and reliability of f _X obtained from the observed trajectories of MLVs and cells using our formulation of the FM-DEP (Eqs. (9) and (11)):While the f _X evaluated from the FM-DEP of a single MLV coincides with that obtained from the force measurement of the same MLV experiencing AC-DEP, the conductivity dependencies of f _X provide the membrane capacitances of various cells that are in close agreement with the literature values. In other words, it has been validated theoretically and experimentally that the FM-DEP in the WBL limit can be mimicked by the time-varying AC-DEP induced by the AC wave with its frequency changing continuously according to the periodic function of f (t ). The simple view applies to other electrokinetics, including the twDEP and the electrorotation by applying the FM wave that has the spatial dependence of the phase as well as the magnitude. The AC- and FM-DEPs are associated with the real part of the dielectric spectra (or the CM factor), whereas the electrokinetics due to the spatial gradient of the phase reflect the imaginary part of the CM factor as mentioned before. Therefore, the application of the FM wave to either twDEP or electrorotation will be required for completing the dielectric characterization (the dielectric spectroscopy, in general) using the electrokinetics.

We have treated microparticles such as MLVs and cells for the precise tracking of particle trajectories. In these experiments, sedimented particles as well as floating ones have been observed; we need to increase the magnitude of electric field for inducing the DEP of the sedimented particles which are likely to be aggregated. Accordingly, we have used the plug-in system for applying the FM wave to a targeted particle floating above the substrate.

It is promising to further develop the FM-DEP method for smaller particles with their sizes of submicron to nanoscale, such as dispersed carbon nanotubes, thereby opening up the possibility of real-time spectroscopy using the FM-DEP as described below. When we apply the FM wave to the smaller colloids using the on-chip systems whose electrode configuration is designed to create a constant gradient of the applied electric field, the time-varying velocity vector v (t ) of the FM-DEP caused by the time dependence of the FM-DEP force is ascribed to the variation in χ (f ) (or the real part of the CM factor):it is found from Eqs. (9) and (12) that

Hence, measuring the velocity vector v (t ) of a submicron to nanoparticle could provide the frequency dependence of the real part of the CM factor directly, which would be nothing but the electrokinetic FM spectroscopy.

Abkürzungen

AC:

Alternating current

BL:

B cell leukemia

CM:

Clausius-Mossotti

DEP:

Dielectrophoresis

DOPC:

1,2-Dioleoyl-sn-glycero-3-phosphatidylcholine

FM:

Frequency modulated

MLV:

Multilamellar vesicle

RB:

Red blood

RMS:

Root mean squared

TL:

T cell leukemia

twDEP:

Traveling wave dielectrophoresis

WBL:

Wide band limit