Kontrollierbare Valley-Polarisation mit Silicen-Doppelliniendefekten aufgrund der Rashba-Spin-Bahn-Kopplung

Einführung

Silicen, ein monolithisches Monoschicht-Wabengitter aus Siliciumatomen, ist eine potenziell attraktive Alternative zu Graphen für Valleytronic-Anwendungen. Die Struktur mit geringem Buckel führt zu einer relativ großen Spin-Bahn-Kopplung (SOC) in Silicen, und an den Dirac-Punkten K . wird eine beträchtliche Energielücke von ungefähr 1,55 meV geschätzt und K ^′ [1] Anders als bei Graphen ist die niederenergetische Dispersionsbeziehung von Silicen eher parabolisch als linear. Erleichtert durch die Knickstruktur kann die Bandstruktur von Silicen durch Anlegen eines elektrischen Felds gesteuert werden, und sogar ein topologischer Phasenübergang von einem Quantenspin-Hall-Isolator zu einem Quanten-Tal-Hall-Isolator kann auftreten[2, 3]. Silicen wurde erfolgreich auf der Oberfläche von Substraten wie Ag(111), Ir(111) und ZrB2(0001)[4–6] synthetisiert, und seine freistehende stabile Struktur wurde auch in mehreren theoretischen Studien vorhergesagt[7 ]. Am wichtigsten ist, dass experimentell ein Silicen-Feldeffekttransistor (FET) bei Raumtemperatur erfolgreich beobachtet wurde[8]. Die Abstimmbarkeit des elektrischen Felds und die Kompatibilität mit bestehenden Silizium-basierten Geräten machen Silicen zu einem potentiellen zweidimensionalen Material für die Anwendung in der Valleytronics der nächsten Generation.

In zweidimensionalen (2D) Materialien wie Graphen und Übergangsmetalldichalkogeniden (MoS₂ , etc.), sind Korngrenzen zwischen zwei Materialdomänen mit unterschiedlichen kristallographischen Orientierungen die ideale Wahl, um die Talpolarisation zu erreichen, und haben beträchtliche Aufmerksamkeit auf sich gezogen[9–14]. Kürzlich wurden die Extended Line Defects (ELDs) in Silicen ausgiebig nach First-Principles-Rechnungen[15, 16] untersucht, und das 5-5-8 ELD (im Folgenden als „Linedefekt“ abgekürzt) wurde als die stabilste und am leichtesten zu bildende Struktur Die Spin- und Talpolarisation des Silicen-Liniendefekts wurde theoretisch untersucht[17–19] Die Bildung eines Liniendefekts kann als das Zusammenfügen der Zickzack-Kanten zweier Si-Körner durch die adsorbierten Si-Atome, wobei jede Seite des Liniendefekts ein Pseudokantenzustands-ähnliches Verhalten zeigt und die Korngrenzen der Zickzackkante als Pseudokante fungieren.16 Offensichtlich ist ein solches Gitter spiegelsymmetrisch zur Linie Defekt und die entsprechenden Gittervektoren in den durch den Defekt getrennten „linken“ und „rechten“ Domänen sind gegensätzlich[10, 11]. /B Untergitter und Talindexe werden beim Überqueren des Fehlers ausgetauscht. Der Liniendefekt ist für die Quasiteilchen in Graphen semitransparent, und bei einem hohen Einfallswinkel tritt eine Hochtalpolarisation auf. Die Talpolarisation ist q _y (die Gruppengeschwindigkeit des Elektrons entlang des y Richtung) über den Leitungsfehler abhängig. Für Graphen, das eine lineare Dispersion und eine konstante Gruppengeschwindigkeit aufweist, kann die Talpolarisation im großen |q . nahezu 100 % erreichen _y | (entspricht einem großen Einfallswinkel), während er mit |q . abnimmt _y | verringert und verschwindet als |q _y |∼0 [9, 14]. Silicen hat dagegen zwei unterschiedliche Transmissionseigenschaften [17, 18]:Erstens werden die beiden Täler ununterscheidbar, da die Fermi-Energie aufgrund der parabolischen Dispersionsbeziehung nahe der Bandkante liegt, und zweitens ist die Transmission wegen der helikalen Kantenzustand, der auf beiden Seiten des Linienfehlers invers fließt, wie in Fig. 1c gezeigt. Natürlich ist das System mit SOC in einem bestimmten RSOC ein vielversprechender Kandidat für einen effizienten Spin-FET. Der RSOC erzeugt ein wirksames Magnetfeld in der Ebene und induziert die Spinpräzession, die senkrecht zur Begrenzungsebene injiziert wird. Die Spinpolarisation[20] und -inversion[21] wurden in gesteuerten Silicen-Nanobändern untersucht. Theoretische Rechnungen haben gezeigt, dass das Energieband von Silicen durch RSOC signifikant moduliert werden kann [22, 23]. Zum Beispiel, bei einem relativ starken RSOC, das Spin-Down (-Up) Band bei K (K ^′ ) verschiebt sich das Tal nach oben, während die anderen Spinbänder im Leitungsband unverändert bleiben. Unter Berücksichtigung der besonderen Transmissionseigenschaft im Silicen-Leitungsdefekt und der Wirkung von RSOC in Silicen werden die praktischen vollelektrischen Schemata zur Erzeugung tal-polarisierter Ladungsträger machbar.

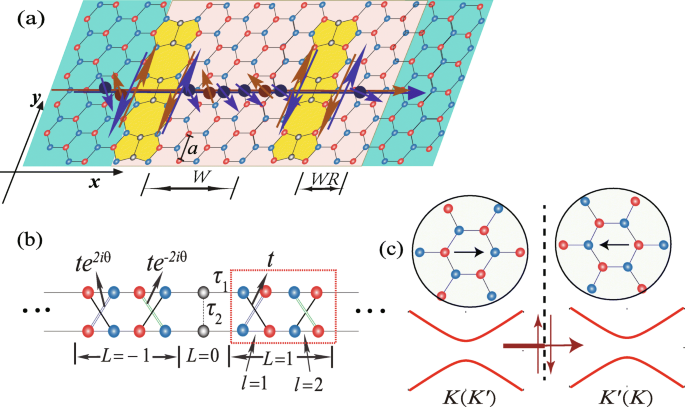
a Schematische Darstellung des Präzessionsprozesses der Zustände (K ,↑ )(rote Kugel) und (K ^′ ,↓ )(blaue Kugel) durch eine Silicenschicht mit zwei parallelen Liniendefekten, wobei der blaue (rote) Kreis das A . bezeichnet (B ) Untergitter. Die Staaten (K ,↑ ) und (K ^′ ,↓ ) zirkulieren entlang der Pseudokante, und es wird angenommen, dass sowohl der RSOC als auch das elektrische Feld in der französischen Grauzone existieren. W (W =2) und WR (WR =1) repräsentieren die Breite des Streubereichs in Einheiten von \(\sqrt {3}a\). b Das vereinfachte Gittermodell des unendlichen Silicens mit einem Liniendefekt, wobei θ =k _y a und das gepunktete Rechteck entspricht einer Superzelle. In der Elementarzelle werden die Gitterpunkte durch eine Reihe von Indizes (L,l ). c Die Transmission für einen Spinzustand im K (K ^′ ) Tal über Leitungsdefekt mit Inversionsdomänengrenzen. Die Einschübe zeigen die Orientierung des Kristallgitters in den beiden durch den Liniendefekt getrennten Domänen (gestrichelte Linie). Die dicken/dünnen Linien zeigen an, dass die Transmission über den Liniendefekt eingeschränkt ist, da die helikalen Kantenzustände invers entlang der Pseudokante fließen

In diesem Artikel schlagen wir einen effizienten Weg vor, die Dirac-Fermionen verschiedener Täler unter Verwendung der Silicen-Doppelliniendefekte zu polarisieren, wodurch eine unterschiedliche Talpolarisation durch Nutzung des elektrischen Felds in Silicen erzeugt wird. Unsere Ergebnisse zeigen, dass, wenn die Fermi-Energie nahe der Unterseite des Leitungsbandes liegt, die Schwingungsbilder der Transmissionskoeffizienten aus zwei Tälern, die breite oszillierende Spitzen und Tiefpunkte umfassen, zusammenfallen, solange RSOC den intrinsischen SOC überschreitet, während das Vorhandensein von nur ein einzelner Liniendefekt kann die talabhängigen Elektronen nicht zerstreuen. Wenn zwei parallele Liniendefekte beteiligt sind, entwickeln sich die oszillierenden Nadir zu Plateaus ohne Transmission, und eine effektive Modulation des talabhängigen Transports kann realisiert werden, indem die Schwingungsperiodizität der beiden Dirac-Täler mit einem senkrechten elektrischen Feld geändert wird, wobei die Schwingungsperiodizität von die beiden Täler nehmen zu und ab und führen zu der perfekten Talpolarisation an den weiten Peak-Null-Plateau entsprechenden Regionen. Im Experiment kann man einen solchen reinen Talstrom nachweisen, indem man die Änderung der Leitfähigkeit mit dem elektrischen Feld misst. Dieses Phänomen bietet einen anderen Weg zum effektiven Modulieren der Talpolarisation in Silicen-Bauelementen unter Verwendung des RSOC und der elektrischen Felder.

Methoden

Beginnen wir mit dem Schema einer zweipoligen Silicen-Leitungsdefektvorrichtung, wie in 1a gezeigt, in der die Spinpräzession veranschaulicht ist, um den talpolarisierten Strom aufgrund des RSOC und des elektrischen Felds zu erzeugen. Es wird angenommen, dass RSOC auf einer Seite des Linienfehlers mit der Breite W . existiert und WR in Einheiten von \(\sqrt {3}a\), wobei a =3.86 Å ist die Gitterkonstante von reinem Silicen, wie in Abb. 1a gezeigt. Wenn sich die Fermi-Energie am unteren Ende des Leitungsbandes befindet, sind die Zustände (K ,↓ )[ (K ,↓ ) entspricht einem Zustand im Tal K mit ↓ (Down) Spin] und (K ^′ ,↑ ) sind aufgrund der Manipulation des Energiebandes von RSOC in der Lücke. Die anderen beiden Staaten (K ,↑ ) und (K ^′ ,↓ ), zirkulieren aufgrund der Spin-Impuls-Locking-Charakteristik von SOC[24] entlang der Pseudokante, wie in Abb. 1a gezeigt. Für einen bestimmten Spin-Zustand fließt es entlang der Pseudokante mit entgegengesetzten Richtungen auf beiden Seiten des Leitungsdefekts, was als Filter wirken und die Übertragung über den Leitungsdefekt einschränken kann, wie in Abb. 1c dargestellt.

Ein Gittermodell in der Tight-Binding-Darstellung wird verwendet, um das Liniendefektsystem mit RSOC als [17, 22]

wobei \(c_{i\alpha}^{\dag}\) und \(c_{i_{y}\alpha,\gamma /\delta }^{\dag}\) den Elektronenerzeugungsoperator mit Spin α auf der Silicen-Site i bzw. der Leitungsdefekt und 〈〉/〈〈〉〉 läuft über alle Nächste-/Nächster-Nächster-Nachbar-Hopping-Sites. Die ersten drei Terme bezeichnen das Springen zum nächsten Nachbarn und die Parameter t ,τ ₁ , und τ ₂ bezeichnen verschiedene Next-Neighbor-Hopping-Energien im Tight-Binding-Modell, wie in Abb. 1b gezeigt. Der vierte Term ist der effektive SOC mit dem Hopping-Parameter t _also , und ν _ij =±1 für das Springen im Gegenuhrzeigersinn (im Uhrzeigersinn) zwischen den nächstgelegenen Nachbarorten in Bezug auf das positive z -Achse. Eine theoretische Untersuchung [16] hat gezeigt, dass die beiden nächsten Si-Atome in der Defektregion relativ identisch mit denen in der unberührten Region sind und dass alle Si-Atome in der sp . verbleiben ² −sp ³ hybridisierten Zustand. Daher ist es sinnvoll, τ . einzustellen ₂ =τ ₁ =t . Im fünften Term, Δ _z ist das gestaffelte Untergitterpotential, das aus einem elektrischen Feld senkrecht zur Silicenschicht entsteht, und μ _ich =±1 für das A (B ) Seite? ˅. Der letzte Term stellt den extrinsischen RSOC-Term dar, wobei t _R ist der Spin-Bahn-Hopping-Parameter von Rashba. d _ij ist der Einheitsvektor, der von der Stelle j . zeigt zu i , und \(\vec{\sigma}=(\sigma^{x},\sigma^{y},\sigma^{z})\) in Gl. 1 ist der Vektor der reellen Spin-Pauli-Matrizen. Der RSOC entsteht durch ein externes Potential, das entweder durch ein elektrisches Gate, eine Metallatomadsorption oder ein Substrat angelegt wird [20, 25], das die Strukturinversionssymmetrie von Silicen dramatisch brechen kann. Insbesondere wird der extrinsische RSOC, der vom elektrischen Feld herrührt, ignoriert, da er sehr schwach ist.

Die ELDs von Silicen sind in Abb. 1a dargestellt, die sich immens entlang des y . erstreckt Richtung. Die Translationssymmetrie der Gitterstruktur entlang des y Richtung zeigt an, dass k _y eine Erhaltungsgröße ist und dass die Erzeugungs-(Vernichtungs-)Operatoren gemäß der Fourier-Transformation wie folgt umgeschrieben werden können (der Spinindex wird ignoriert)[17]:

Dann ist die Hamilton-Matrix in Gl. 1 wird entkoppelt in \(H=\sum_{k_{y}}H_{k_{y}}\), wobei \(H_{k_{y}}\) in folgender Form beschrieben werden kann:

wobei \(\varphi_{i,l}^{\dag}=\left [ c_{{{k}_{y}},i,l,A\uparrow}^{\dag}, c_{{{ k}_{y}},i,l,A\downarrow}^{\dag}, c_{{{k}_{y}},i,l,B\uparrow}^{\dag},c_{ {{k}_{y}},i,l,B\downarrow}^{\dag}\right]\), i in der Indexmenge (i,l ) repräsentiert die Position einer Superzelle \((\bar {i}=-i)\) und l =1 oder 2 bezeichnet verschiedene Zickzackketten in einer Superzelle, wie in dem gestrichelten Rechteck in Fig. 1b gezeigt. \(\hat {T_{ll'}}\) repräsentiert die Hamiltonsche Matrix jeder Zickzackkette (l =l ^′ ) in einer Superzelle oder das Zusammenspiel verschiedener Zickzackketten (l l ^′ ).

Es wird darauf hingewiesen, dass die beiden Täler K und K ^′ werden jetzt auf [0,±π . gecastet /3a ] aufgrund des Einfügens des Leitungsfehlers. Die Übertragungsmatrix der η (η =K /K ^′ ) Valley wird mit der verallgemeinerten Landauer-Formel[26, 27] berechnet,

wo

und

Hier gilt \(-Im\Sigma_{L,R}=-\left(\Sigma_{L,R}^{r}-\Sigma_{L,R}^{a}\right)/ 2i\ ) sind positive semidefinite Matrizen mit einer wohldefinierten Matrix-Quadratwurzel, wobei \(\Sigma_{L,R}^{a}=\left [\Sigma_{L,R}^{r}\right ]^{ \dag }\) sind die verzögerte/fortgeschrittene Selbstenergie der linken/rechten Leitung. Die 16×16-Submatrix G ^r ist die retardierte Green-Funktion, die die erste und letzte Superzelle entlang des x . verbindet Richtung und kann mit der rekursiven Methode der Greenschen Funktion berechnet werden. Die Gesamtübertragungskoeffizienten der η Tal sind \(T_{\eta}=T^{\uparrow\uparrow}_{\eta}+T^{\uparrow\downarrow}_{\eta}+ T^{\downarrow \uparrow}_{\eta }+T^{\downarrow \downarrow }_{\eta}\) und die Spinpolarisation P _s und Talpolarisation P _η kann gegeben werden durch

Ergebnisse und Diskussion

Bei den Berechnungen der spinabhängigen Transmissionskoeffizienten setzen wir τ ₂ =τ ₁ =t =1 als Energieeinheit, die SOC-Stärke t _also =0,005t , und die Fermi-Energie E _f =1.001t _also , die sich am unteren Ende des Leitungsbandes befindet. Die Breite des Streubereichs beträgt W =1000 für den Einzellinienfehler und eine zusätzliche Breite WR=1000 wird auch für die beiden Parallellinienfehler berücksichtigt, wie in Abb. 1a gezeigt.

Abbildung 2 zeigt die spinerhaltenen/Spin-Flip-Transmissionskoeffizienten von Tal \(\eta, T^{sc}_{\eta}/T^{sf}_{\eta}\), als Funktion des Vorfalls Winkel α (a) und der RSOC-Stärke t _R (b–d). Abbildung 2a–c entspricht dem Fall des Einzellinienfehlers und (d) steht für den Fall der zwei parallelen Linienfehler. Es wird gezeigt, dass bei einem bestimmten t _R (zum Beispiel t _R =5t _also wie in Abb. 2a) sind die spinabhängigen Transmissionskoeffizienten \(T^{sc}_{K}/T^{sf}_{K}\) wegen der parabolischen Dispersionsbeziehung konstant und unabhängig von den Einfallswinkeln , wie in Abb. 2a gezeigt. Daher können wir in den folgenden Berechnungen den Einfallswinkel α . verwenden =0 als Beispiel. Für ein schwaches t _R , tritt aufgrund der Rashba-Aufspaltung ein Oszillationsphänomen auf, das dem in einem zweidimensionalen Elektronengas ähnlich ist [26, 27], wie im Einschub von Abb. 2b gezeigt. Als t _R erhöht (t _R >t _also ), \(T_{K}^{\uparrow \uparrow }\) und \(T_{K}^{\uparrow \downarrow }\) haben die gleiche schwingende Periodizität und fast die gleichen Beträge wie t _R die aus einigen Schwingungspeaks und -nadiren besteht, während \(T_{K}^{\downarrow \downarrow}/T_{K}^{\downarrow \uparrow }\) gegen Null geht, weil die Fermi-Energie in ihrer Lücke liegt, da in Abb. 2b gezeigt. Somit ist der Gesamttransmissionskoeffizient von K Valley wird hauptsächlich durch den Spin-Up-Zustand beigetragen. Tatsächlich sind die Schwingungsbilder der beiden Täler, K und K ^′ , zusammenfallen, während die Transmissionskoeffizienten von K ^′ Tal wird hauptsächlich von den Spin-Down-Elektronen beigesteuert.

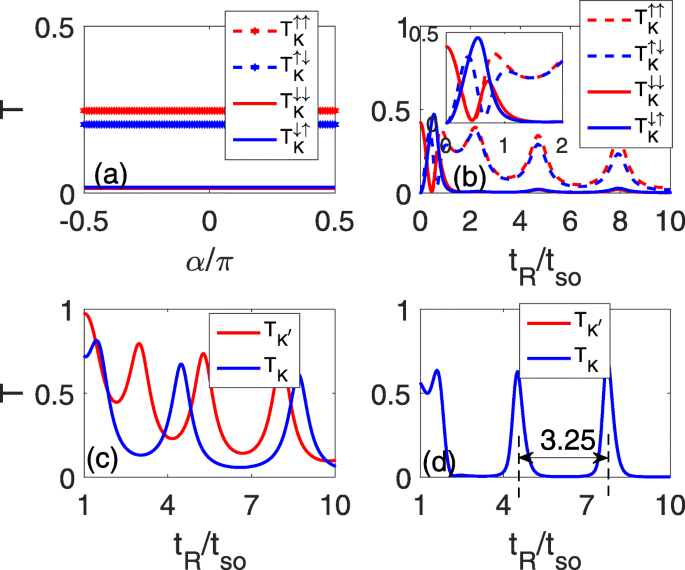
Spinerhaltungs- und Spin-Flip-Transmissionskoeffizienten als Funktionen der Einfallswinkel α um t _R =5t _also in a und als Funktionen der RSOC-Stärke t _R in b –d , wobei a -c sind für den Einzellinienfehler und d ist für die beiden parallelen Liniendefekte mit Δ _z =0,2t _also in c

Bei Vorhandensein eines senkrechten elektrischen Feldes wird die Talentartung aufgehoben und das Schwingungsverhalten der beiden Täler unterscheidet sich:die Schwingungsperiodizität des K Tal zunimmt, während das des K ^′ Tal nimmt ab, wie in Abb. 2c gezeigt. Es scheint jedoch unmöglich, einen konischen Talzustand mit nur einem einzigen Liniendefekt zu filtern, da die oszillierenden Nadirs eine bestimmte Größe haben. Natürlich kann man das Schwingungsphänomen mit zwei parallelen Leitungsdefekten betrachten, um die Übertragung weiter einzuschränken, wie in Fig. 2d gezeigt. Der Vergleich von Abb. 2b mit d zeigt, dass die Schwingungsspitze schmal und spitz wird, während sich der Schwingungsnadir verbreitert und abschwächt, was die Nullübertragungsplattform bildet. Der Abstand zwischen zwei benachbarten Schwingungspeaks ist auf 3,25t . festgelegt _also , wie durch die beiden gestrichelten Linien in Abb. 2d gekennzeichnet.

Um einen besseren Valley-Filter-Effekt zu erzielen, konzentrieren wir uns auf die Wirkung des senkrechten elektrischen Feldes. Die Ergebnisse dieses Effekts sind in Fig. 3 gezeigt. Wie oben erörtert, ändert sich die Schwingungsperiode der beiden Täler in entgegengesetzter Weise, und die ursprünglichen überlappenden Schwingungsspitzen in Fig. 2d werden aufgehoben. Währenddessen verbreitert und verengt sich das Null-Transmissions-Plateau für T _K bzw. \(T_{K^{\prime}}\), wie in Abb. 3a und b gezeigt. Bei Δ _z =0,15t _also , entwickelt sich der Abstand zwischen den beiden benachbarten Schwingungspeaks zu 3,6t _also für T _K , während es auf 3,1t . reduziert wird _also für \(T_{K^{\prime}}\), wie durch die beiden blauen und roten gestrichelten Linien in Abb. 3a angedeutet. Wenn das elektrische Feld stärker wird, nimmt der Abstand zwischen den beiden benachbarten Schwingungsspitzen für T . weiter zu/ab _K /\(T_{K^{\prime}}\), das ist 5,4t _also /2.8t _also bei Δ _z =0,3t _also , wie in Abb. 3b gezeigt. Die Änderung der Schwingungsperiodizität führt zu den entsprechenden Regionen eines breiten Peak-Null-Plateaus, wo eine perfekte Talpolarisation mit P _η =±1 Plateaus realisiert werden, wie in Abb. 3c und d gezeigt. Gleichzeitig wird gezeigt, dass hohe Spinpolarisation P _s entsteht auch, wenn P _η =±1.

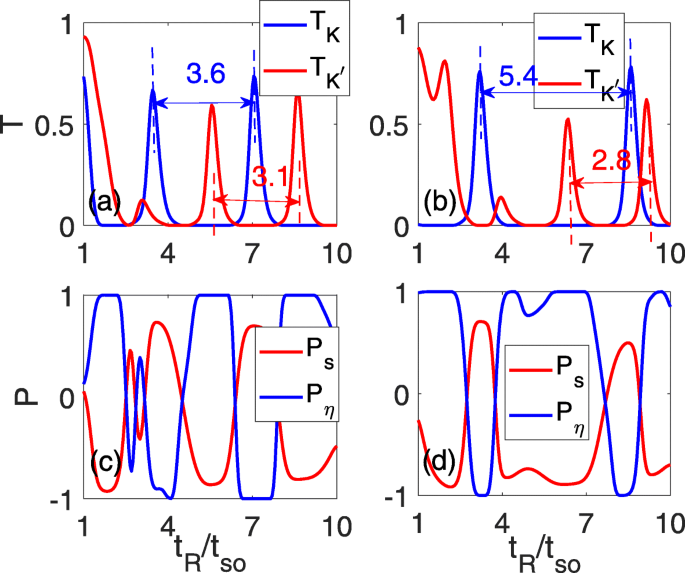
Die gesamten Transmissionskoeffizienten \(T_{K}/T_{K^{\prime}}\) (a , b ) und die Spin/Tal-Polarisation (c , d ) als Funktion der RSOC-Stärke t _R für verschiedene Untergitterpotentiale. Δ _z =0,15t _also in a und c und Δ _z =0,3t _also in b und d; die anderen Parameter sind identisch mit denen in Abb. 2d

Aufgrund der Unkontrollierbarkeit von RSOC ist es jedoch immer noch schwierig, solche reinen Talströme experimentell zu detektieren, obwohl der im Leitungsdefekt induzierte RSOC größer sein kann als der intrinsische SOC. Um den reinen Talstrom bequem experimentell zu untersuchen, untersuchen wir auch die Transmissionskoeffizienten und die Talpolarisation als Funktion des elektrischen Felds, die während eines Experiments kontinuierlich kontrolliert werden können. Es wird gezeigt, dass die perfekte Talpolarisation mit P _η =±1 kann in einem bestimmten Bereich von Δ . auftreten _z und dass es sich von P ändern kann _η =1 bis P _η =−1 mit zunehmendem elektrischem Feld, wie in Abb. 4a gezeigt. Für ein bestimmtes t _R (zum Beispiel t _R =7,2t _also , wie in Abb. 4a gestrichelt angedeutet), schwingen die Transmissionskoeffizienten \(T_{K}/T_{K^{\prime}}\) mit Δ _z , wobei die breiten Transmissionsspitzen des K (K ^′ ) Tal entsprechen den Nulltransmissionsplateaus des K ^′ (K ) Schlucht. Die gesamten Transmissionskoeffizienten werden im Wesentlichen von einem Tal beigesteuert, wenn sich das elektrische Feld ändert, und eine perfekte Talpolarisation kann immer um den Maximalwert von \(T_{K}/T_{K^{\prime }}\) auftreten, wie in gezeigt Abb. 4b. Da die Fermi-Energie von der Bandkante abweicht, kann die perfekte Talpolarisation auch bei E . noch überleben _f =1,5t _also , wo die Plateaubeziehung gut aufrechterhalten werden kann, wie in Abb. 4c gezeigt. Während eines Experiments kann man die talpolarisierten elektrischen Ströme von links nach rechts mit einer experimentell messbaren Größe wie dem Leitwert, der proportional zum Gesamttransmissionskoeffizienten ist, analysieren. Die maximale Leitfähigkeit zwischen zwei minimalen Werten (manchmal sind sie null) sollte von einem Tal ausgehen. Den Betrag des Leitwerts können wir nach der Formel \(G=\frac{e^{2}}{h}\int _{-k_{F}}^{k_{F}}T\frac {dk_ {y}}{2\pi /L_{y}}=\frac {e^{2}}{h}\frac {Ly\sqrt {E^{2}-t^{2}_{so}} }{2\pi \hbar v_{F}}2T\) [28], wobei L _y =2a ≈7.72Å ist die Breite des Silicenliniendefekts, v _F =5,5×10 ⁵ m /s ist die Fermi-Geschwindigkeit, \(\hbar=h/2\pi\) ist die reduzierte Planck-Konstante mit \(\phantom {\dot{i}\!}h=4.13566743\times 10^{-15}eV\cdot s, T=T_{K}+T_{K'}\) ist der Gesamttransmissionskoeffizient und E ist die Ortsenergie der einfallenden Elektronen. Dann beträgt der Leitwert ungefähr \(G\approx \left [0,7T\sqrt {E^{2}-t^{2}_{so}}/eV\right ]\frac {e^{2}}{ h}\). Es wurde auch festgestellt, dass die Energie vor Ort auf der Einfallsseite auf E . angehoben wird =0,15t (t =1.6eV ), ändern sich die Transmissionskoeffizienten der beiden Täler im Vergleich zu Fig. 4c aufgrund der Spin- und Impulserhaltung nur wenig und die Transmissionspeak-Null-Plateau-Beziehung bleibt unverändert, wie in Fig. 4d gezeigt. In diesem Fall beträgt die Leitfähigkeit etwa \(G\approx 0.17T\frac{e^{2}}{h}\), was beträchtlich ist und im Experiment nachweisbar ist. Das Energiefenster zur Beobachtung dieses Phänomens beträgt etwa 0,5t _also (t _also <E <1.5t _also ), die proportional zu t . ist _also . Im Experiment ist es nicht schwierig, die Fermi-Energie nahe der Bandkante zu kontrollieren, und die SOC-Lücke kann durch die Nähe zur Bi(111)-Doppelschicht[29] sogar radikal auf 44 meV vergrößert werden, was den Energiebereich zum Nachweis des reinen . erheblich verbessern kann Talstrom. Darüber hinaus kann das Rechenmodell auch auf andere Gegenstücke von Graphen, Germanen[30], Stanen und MoS₂ . mit geringer Knickung angewendet werden [31–36], die noch größere Bandlücken[37, 38] sowie die SOC-Stärken aufweisen (die SOC-Stärke kann für Stanen 0.1eV erreichen[38, 39]). In einem realen Experiment ist es einfach, einen starken RSOC zu realisieren, der den intrinsischen SOC überschreiten kann, indem die Spiegelsymmetrie in der Ebene mit dem speziellen Substrat gebrochen wird[40]. Daher kann dieses Schema im Experiment vollständig durchführbar sein.

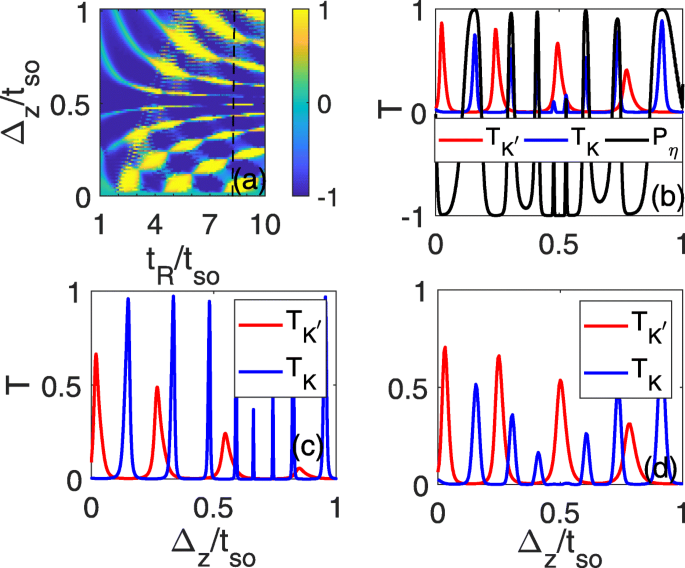
Talpolarisation a und \(T_{K}/T_{K^{\prime}}\) (b –d ) als Funktionen von Δ _z und t _R . t _R =7,2t _also in (b –d ), E _f =1,5t _also in c und d , und die Energie vor Ort beträgt E =0,15t in der linken Elektrode in d; alle anderen Parameter sind identisch mit denen in Abb. 2d