Roboter-Euler-Winkel:Die wesentliche Grundierung

Es ist schwer, sich mit Roboterrotationen vertraut zu machen, nicht wahr? Euler-Winkel sind ein Schmerz im Nacken. Hier ist die grundlegende Grundierung, um den Schmerz zu lindern.

Orientierungen! Sie bringen mich nur dazu, mir die Haare auszureißen. Wenn Sie jemals die Endposition eines Roboters mithilfe von Koordinaten und Drehungen programmieren mussten, wissen Sie, wovon ich spreche.

Auf den ersten Blick erscheint das Einstellen der Pose des Endeffektors Ihres Roboters einfach, nicht wahr?

Sie sagen einfach:„Ich möchte das Werkzeug des Roboters hier bewegen Ort und ich möchte, dass er auf hier zeigt Richtung.“

Intuitiv wissen Sie genau, welche Ausrichtung das Werkzeug haben soll. Wenn es jedoch darum geht, die Orientierung mit genauen Zahlen zu beschreiben, wird diese einfache Aufgabe plötzlich zu einem Wirrwarr.

Warum Roboterorientierungen schwer zu verstehen sind

Es ist einfach, die X-, Y-, Z-Koordinaten (translational) eines Roboterwerkzeugs zu beschreiben.

Um eine Übersetzung zu beschreiben, geben Sie einfach die Koordinaten ein — z.B. Punkt[X, Y, Z] =[100, 1000, 1500] mm – und es gibt nur einen Ort, auf den sich dies beziehen könnte, vorausgesetzt, Sie verwenden dieselbe Basisreferenz. Es kann nur 100 mm entlang der X-Achse, 1 Meter entlang der Y-Achse und 1,5 Meter entlang der Z-Achse bedeuten.

Aber wie beschreiben Sie die Ausrichtung des Werkzeugs?

Man könnte sagen:
Drehung[XYZ] =[5, 45, 15]°
man könnte aber auch sagen (Zahlen runden)
Rot[XY'Z”] =[-7,9, 44,7, 16,2]°
oder
Rot[ZY'Z”] =[7,9, 45,2, 5,0]°
oder Gerade
Quaternion[q1-q4] =[0.9, -0.1, 0.4, 0.1]

 All dies bezieht sich auf genau dieselbe Ausrichtung!
Was es noch umständlicher macht, ist, dass verschiedene Roboterhersteller unterschiedliche Konventionen verwenden. Das alles kann ein bisschen Kopfschmerzen bereiten, selbst wenn Sie mit 3D-Geometrie vertraut sind.

Das Problem:Wir denken einfach nicht in Rotationen

Das eigentliche Problem ist, dass wir einfach nicht in Rotationen denken.

Wir verstehen Translationskoordinaten intuitiv, weil wir sie in unserem Alltag verwenden (z. B. "Es ist im zweiten Regal unten, vier Bücher von links." ). Wenn wir jedoch eine Ausrichtung beschreiben müssen, greifen wir darauf zurück, mit unserem Finger zu zeigen und zu sagen:"Es geht in diese Richtung."

Leider brauchen Roboter genauere Informationen als ein vages „dort drüben.“

Was wir brauchen, ist ein solides Verständnis der Euler-Winkel.

Was sind Euler-Winkel?

Lassen Sie uns einen Schritt zurücktreten und mit den Grundlagen beginnen.

Die gebräuchlichste Methode zur Beschreibung der Roboterausrichtung sind Euler-Winkel. Der Euler-Winkel besteht aus drei Zahlen, die jeweils eine Drehung um eine Achse beschreiben. Abhängig von der Reihenfolge der Drehungen gibt es unterschiedliche Euler-Winkel-Konventionen.

Lassen Sie uns dies zunächst zu einem einachsigen Beispiel vereinfachen.

Stellen Sie sich einen Kompass vor.

Oft bezieht sich die Z-Achse der Welt auf die Achse, die sich vom Himmel bis zum Boden erstreckt. Sie können sich also vorstellen, dass die Nadel auf einem Kompass eine Drehung um die Z-Achse ist (mit dem Namen Rot[Z]). Wenn Sie den Kompass flach vor sich halten und der Pfeil auf 135° zeigt, bedeutet dies, dass sich Norden über Ihrer linken Schulter befindet, sodass Sie derzeit nach Südosten blicken. Es spielt keine Rolle, wo Sie den Kompass platzieren (auf dem Boden, auf Ihrem Kopf usw.), wenn er dieselbe Ausrichtung hat, beträgt der Winkel immer 135°.

So weit, so einfach.

Unser Kompass hat nur einen Rotationswert (z. B. Rot[Z]), aber um eine beliebige 3D-Ausrichtung zu beschreiben, benötigen wir drei Werte. Hier wird es etwas komplizierter.

Andere Methoden zur Beschreibung von Roboterorientierungen sind Quaternionen oder Posen (4×4-Matrizen).

Lass uns Hand anlegen

Von nun an wird es für Sie hilfreich sein, eine interaktive visuelle Hilfe zu haben.

Ich schlage vor, dass Sie eine kostenlose Kopie von RoboDK unter diesem Link herunterladen, was es sehr einfach macht, Referenzrahmen zu visualisieren und die resultierenden Koordinaten zu sehen.

Starten Sie RoboDK und erstellen Sie einen Referenzrahmen, indem Sie auf die Schaltfläche „Referenzrahmen hinzufügen“ klicken oder die Option im Programmmenü auswählen. In der Mitte des Bildschirms sollte ein roter, grüner und blauer Rahmen erscheinen.

Sie können den Rahmen wie folgt drehen:Halten Sie die Alt-Taste gedrückt, klicken Sie dann auf einen der erscheinenden gebogenen Pfeile und ziehen Sie ihn.

Wie man ein Flugzeug fliegt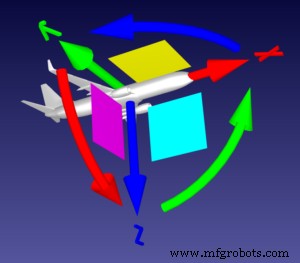

Lassen Sie uns die Analogie eines Flugzeugs verwenden, wie es sehr deutlich im Roboterforum beschrieben wird.

Stellen Sie sich vor, der Referenzrahmen ist eine Ebene. Die Spitze des geraden, roten Pfeils (die X-Achse) ist die Spitze seines Nasenkegels und der gerade, grüne Pfeil (die Y-Achse) ist sein linker Flügel.

In diesem Fall erfüllt das Bewegen der gekrümmten Pfeile die folgenden Funktionen:

• Gebogener roter Pfeil =Rot[X]:Die Rolle des Flugzeugs, die es dem Flugzeug ermöglicht, sich um seine horizontale Achse zu drehen.
• Gebogener grüner Pfeil =Rot[Y]:Die Steigung des Flugzeugs, die den Nasenkegel nach oben oder unten zeigt.
• Gebogener blauer Pfeil =Rot[Z]:Das Gieren des Flugzeugs, das die Richtung bestimmt, in die das Flugzeug fliegt.

Wenn der Pilot wollte, dass das Flugzeug allmählich nach links und nach unten dreht, würde sich das Flugzeug nicht nur um die Z-Achse drehen – so funktionieren Flugzeuge nicht.

Stattdessen würde das Flugzeug:

1. Neige den Nasenkegel nach unten:Rot[Y]
2. Rolle das Flugzeug nach links:-Rot[X]
3. Gieren nach links:Rot[Z]

Diese ganze Bewegung würde als Rot[XYZ] dargestellt werden. Versuchen Sie, den Rahmen in RoboDK selbst ein wenig zu verschieben, bis Sie mit diesen Konzepten vertraut sind.

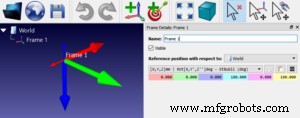
Doppelklicken Sie dann auf den Namen des Frames oben links im Hauptfenster, um das Fenster „Frame-Details“ aufzurufen.

Eine Ausrichtung, mehrere mögliche Drehungen

Probieren Sie mit RoboDK die folgenden Aufgaben aus.

Setzen Sie den Frame vor jeder Aufgabe zurück, indem Sie das „Hamburger“-Menüsymbol (drei horizontale Linien) im Bereich „Frame-Details“ öffnen und „Zurücksetzen (Identität festlegen)“ auswählen.

P>

1. Wählen Sie das Dropdown-Menü über den Koordinaten und wählen Sie die Stäubli-Rotation (X->Y’->Z”) anstelle von Generic.
2. Drehen Sie den Rahmen so, dass Blau (Z) nach unten und Rot (X) nach hinten zeigt (d. h. beide sind von ihrer Startposition umgedreht und Grün (Y) ist dieselbe Startposition), aber tun Sie es nur also durch Drehung um die Y-Achse.
3. Setzen Sie den Rahmen zurück und bewegen Sie ihn dann erneut auf die gleiche Drehung. Verwenden Sie diesmal jedoch nur eine Z-Drehung und dann eine X-Drehung.
4. Setzen Sie den Rahmen zurück und bewegen Sie ihn dann erneut auf die gleiche Drehung. Verwenden Sie diesmal jedoch nur eine X-Drehung und dann eine Z-Drehung.

Wie Sie sehen können, kann es mehrere Möglichkeiten geben, dieselbe Ausrichtung zu erreichen.

Die erste Methode könnten wir Rot[Y] nennen, da sie nur eine Drehung um die Y-Achse beinhaltet. Die zweite Methode könnten wir Rot[Z, X’] nennen, da sie eine Drehung um die Z-Achse und eine Drehung um die neue X-Achse beinhaltet. Die dritte würden wir Rot[X, Z’] nennen. Das Strichsymbol bedeutet, dass die Drehung in Bezug auf die letzte Bewegung statt auf die statischen Achsen erfolgt.

Dies ist das grundlegende Konzept hinter Euler-Winkeln. Sie können einen Rahmen auf mehrere Arten in dieselbe Ausrichtung drehen, indem Sie die Reihenfolge der Achsen und Drehungen ändern.

Verschiedene Roboterhersteller haben unterschiedliche Rotationskombinationen gewählt. Beispielsweise verwendet Stäubli eine XY’Z”-Konvention, Adept verwendet eine ZY’Z”-Konvention, KUKA verwendet eine ZY’X”-Konvention und Fanuc &Motoman verwenden eine XYZ-Konvention. Andererseits verwendet ABB Quaternion und Universal Robots verwendet einen Orientierungsvektor. Aber alle Konventionen können verwendet werden, um jede Orientierung im Raum darzustellen.

Weitere Informationen finden Sie in der RoboDK-Dokumentation.

Testen Sie verschiedene Roboterkonventionen

Hoffentlich macht das langsam Sinn. Dies ist jedoch nur der Anfang. Um die Euler-Winkel-Konventionen in RoboDK wirklich zu beherrschen, finde ich es nützlich, mit der Software herumzuspielen, indem Sie dieser Anleitung folgen.

Sie können den Effekt Ihrer Drehungen in Zahlen in den hellblauen, violetten und gelben Feldern im Bereich „Rahmendetails“ sehen.

Standardmäßig wird die generische XYZ-Konvention für neue Referenzrahmen gewählt. Versuchen Sie, verschiedene Roboterhersteller aus dem Dropdown-Menü über den farbigen Kästchen auszuwählen. Versuchen Sie, numerische Werte in die Felder einzugeben, um deren Auswirkungen auf das Referenzsystem zu sehen.

Für ein ausführliches Tutorial zu Euler-Winkeln kann ich auch diese Seite auf Mecademic empfehlen.