polarisationsabhängige Quasi-Fernfeld-Superfokussierungsstrategie von Nanoring-basierten plasmonischen Linsen

Hintergrund

Neben der Entwicklung der hochauflösenden Bildgebung [1], der Teilchenbeschleunigung [2], der quantenoptischen Informationsverarbeitung [3] und der polarisationsabhängigen optischen Datenspeicherung [4] werden in diesen Regionen oberflächenplasmonische Geräte durch Modulation der Plasmonenresonanz im Subwellenlängenbereich. Die plasmonische Linse (PL) als typisches Gerät besitzt die perfekte Abbildungsfähigkeit, die erstmals 2000 von J. B. Pendry vorgeschlagen wurde [5], und die optische Abbildung unterhalb der Beugungsgrenze wurde experimentell von X. Zhang et al. 5 Jahre später [6]. Die Abbildungsebene war jedoch auf das äußerste Nahfeld beschränkt, da die evaneszenten Wellen exponentiell abnahmen, was auf ein divergentes optisches Feld hinweist. Diese Einschränkung macht es für Standard-Lichtmikroskope nicht praktikabel [7].

In den letzten Jahren wurden mehrere Nanostruktur-basierte PLs untersucht [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. Diese PLs können nicht nur die plasmonische Fokussierung in der Ebene [8] oder im Nahfeld [9] realisieren, sondern können auch die Fokussierungsfähigkeit im Fernfeld [10,11,12,13] besitzen, die im Allgemeinen durch die Abtastoptik abgebildet wurden Mikroskop [14]. Diese PLs zeigten jedoch große Schwierigkeiten, die Fokussierung über die Beugungsgrenze hinaus zu realisieren, bis die Dispersionsbeziehung des Metall-Isolator-Metall (MIM)-Wellenleiters für die Nanoschlitz-basierten PLs verwendet wurde, um die Phase auf der Subwellenlängenskala zu modulieren [11 , 15,16,17]. Die präzise Phasenmodulation trägt zu der Brennlinie unterhalb der Beugungsgrenze bei, und das linear polarisierte Licht wird im Allgemeinen als einfallendes Licht für diese Linsen verwendet. Durch einfaches Ausweiten der ähnlichen Designmethode eindimensionaler Nanospaltlinsen in zwei Dimensionen kann der zirkulare Fokus jedoch nicht realisiert werden, wenn die rotationssymmetrische PL durch das linear polarisierte Licht beleuchtet wurde [18, 19], was auf die starke Polarisationsabhängigkeit hinweist der Fokussierleistung. Darüber hinaus wich die Brennweite stark von der numerischen Berechnung nach der Wellenfront-Rekonstruktionstheorie ab, insbesondere für die Nanoring-basierten PLs [18].

Die nanoringbasierten PLs mit Rotationssymmetrie, die in der folgenden Diskussion der Einfachheit halber als nanoringbasierte plasmonische Linsen (NRPLs) bezeichnet werden, werden als Ersatz für die refraktiven Konversionslinsen in den Subwellenlängen-Fokussiersystemen erkannt. Aber aus der Perspektive der Anregung von Oberflächenplasmonenpolaritonen (SPPs) ist das linear polarisierte Licht für die NRPLs ungeeignet, da die Anregungseffizienz proportional zur radialen elektrischen Feldkomponente des einfallenden Lichts ist. Im Vergleich dazu passt sich das radial polarisierte Licht mit der Zylindersymmetrie in der Polarisation an die Struktureigenschaft von NRPLs an [25]. Zusätzlich wurde dieses polarisierte Licht unter Verwendung einer Donut-förmigen Aperturblende [26, 27] oder einer Fresnel-Zonenplatte [28] angewendet, um den zirkularen Fokus im Subwellenlängenbereich zu realisieren. Daher wurde das radial polarisierte Licht im Allgemeinen als einfallendes Licht von NRPLs verwendet [20,21,22,23]. Verglichen mit der Subwellenlängenfokussierung mit dem Raumfilter besitzen diese PLs die Fähigkeit, die Phase des einfallenden Lichts in den Subwellenlängenwellenleiter zu modulieren. Die Anregung von Oberflächenplasmonenwellen (SP) kann die Übertragung elektromagnetischer Wellen verbessern. Die Superfokussierfähigkeit einer plasmonischen Linse im Fernfeld wurde jedoch nicht demonstriert. Obwohl die zusammengesetzte NRPL vorgeschlagen wurde, die Brennweite zu modulieren [24], konnte die Brennweite jedoch nicht effektiv gesteuert werden und die Energie des elektrischen Felds wird immer noch in der Mitte der Endfläche der Linse konzentriert.

In diesem Beitrag stellen wir den theoretischen Entwurf und die numerische Studie eines NRPL vor, wobei der Schwerpunkt auf der Realisierung der Superfokussierung durch Nutzung der Polarisationseigenschaft des einfallenden Lichts liegt. Wir beschreiben das theoretische Design von NRPLs in unserer Forschung und stellen die Fokussierungsleistung im Ausgabebereich basierend auf der numerischen Finite-Difference-Time-Domain-Simulation (FDTD) bereit. Um die Polarisationsabhängigkeit der Fokussierleistung zu untersuchen, werden linear, zirkular, azimutal und radial polarisierte Lichter für die Beleuchtung berücksichtigt. Wir diskutieren die Eigenschaften der elektrischen Feldverteilung im Ausgabebereich, einschließlich der Fokussierung unterhalb der Beugungsgrenze, der Formen von Brennpunkten und der Modulation der Brennweite, und weisen auf die Bedeutung der koaxialen Bedingung für die Superfokussierungsleistung hin.

Methoden

Die in dieser Arbeit untersuchten NRPLs wurden unter Verwendung der Wellenfront-Rekonstruktionstheorie entworfen, die weithin auf die Nanospalt-basierten PLs angewendet wurde [11, 15]. Um den Fokus an der gewünschten Position zu erreichen, muss die relative Phasenverzögerung beim Durchgang des Lichts durch das i -der einzelne Nanoring muss basierend auf der geometrischen Optik die folgende Bedingung erfüllen:

wobei −Δϕ (r _ich ) ist die relative Phasendifferenz zwischen dem ersten Nanoring im inneren Zentrum und dem i -ter Nanoring, r ist der Radius, λ ₀ ist die Freiraumwellenlänge des einfallenden Lichts, n eine beliebige ganze Zahl ist und f ₀ ist die entworfene Brennweite.

Das grundlegende Element der untersuchten NRPLs sind die im Metallfilm gemusterten Nanoringe. Nach Ref.-Nr. [29], wenn der Durchmesser größer als die Wellenlänge des einfallenden Lichts ist, kann der von metallischen Wänden umgebene Luft-Nanoring dem MIM-Wellenleitermodell angenähert werden, wie der Einschub in Abb. 1 veranschaulicht. Die Phasenverzögerung wird hauptsächlich durch den Realteil definiert der Ausbreitungskonstante β , ausgedrückt als Re(β )•t , wo t ist die Dicke des Nanorings. Basierend auf der Dispersionsbeziehung ist die komplexe Ausbreitungskonstante β kann berechnet werden als:

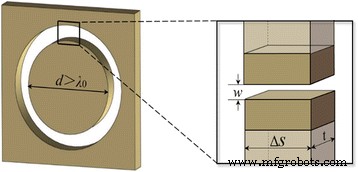
Das MIM-Wellenleitermodell eines einzelnen Nanorings eingebettet in den Goldfilm. Der Einschub gibt eine vergrößerte Ansicht eines beliebigen kleinen Abschnitts des Nanorings

wo k ₀ repräsentiert den Wellenvektor im Vakuum und ε _d und ε _m sind die Permittivität von Dielektrikum bzw. Metall. Basis auf Gl. (2) können wir sehen, dass die Ausbreitungskonstante β ist abhängig von der Breite eines Nanorings. Für die flache Linse mit einer gegebenen Dicke t , die verursachte Phasenverzögerung wird einfach durch die Breite w . bestimmt des einzelnen Nanorings, wenn das Licht durch ihn hindurchtritt. In unserer Forschung wird als Dielektrikum Luft mit der Permittivität ε . festgelegt _d = 1 und der Goldfilm mit einer Dicke von t von 400 nm verwendet, dessen Permittivität bei der einfallenden Wellenlänge von 650 nm ε . beträgt _m = −12,8915 + 1,2044i [15]. Darüber hinaus spielt, wie bereits berichtet [16], auch der Kopplungseffekt des sich ausbreitenden Lichts in den beiden benachbarten MIM-Wellenleitern eine wichtige Rolle für die Phasenverzögerung, insbesondere wenn der Metallwandabstand kleiner als die doppelte Skin-Tiefe δ . ist _m , die geschätzt werden kann durch [30]:

Dementsprechend ist die berechnete Eindringtiefe δ _m beträgt etwa 28 nm. Unter Berücksichtigung des Kopplungseffekts ist ein auf Nanospalten basierender PL mit der Superfokussierungskapazität von 0,38 λ ₀ in Auflösung wurde in unserer früheren Forschung berichtet [16]. Um hier den Einfluss des Polarisationszustands (SOP) auf die Fokussierungsleistung prominent zu analysieren, werden die Abstandswände zwischen zwei benachbarten Nanoringen auf 100 nm ausgelegt, viel größer als 2δ _m um den Kopplungseffekt zu beseitigen.

Das Schema des entworfenen NRPL ist in Fig. 2 gezeigt, und eine Gesamtzahl von 32 konzentrischen Nanoringen ist enthalten, um die Wellenfront zu rekonstruieren. Die Breite des Nanorings für die gewünschte Phasenmodulation reicht von 10 bis 100 nm. Die angestrebte Brennweite f ₀ ist 1300 nm (2 λ ₀ ). Um das MIM-Wellenleitermodell effizient zu nutzen, wird der minimale Durchmesser des innersten Nanorings auf 800 nm eingestellt. Um die in unserer vorherigen Arbeit [15] diskutierte Fokusverschiebung zu vermeiden, beträgt die Gesamtphasendifferenz außerdem 10π mit einer vorhergesagten numerischen Apertur (NA) von 0,96. Daraus ergibt sich die theoretische Rayleigh-Beugungsgrenze, berechnet aus 0,61 λ ₀ /NA [31], beträgt 413 nm (~0,64 λ ₀ ).

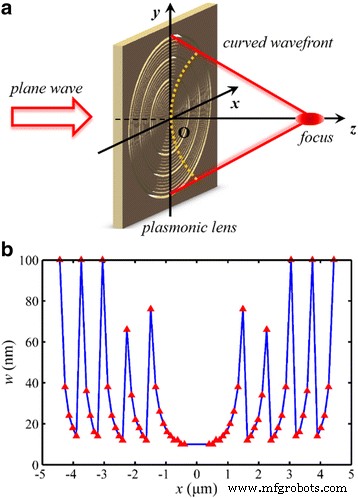
Schema des NRPL. a Normalerweise beleuchtet das einfallende Licht das Objektiv. b Strukturelle Parameter des Objektivs. Die Koordinatenwerte der roten Dreiecke repräsentieren den Radius r und Breite w des entsprechenden Nanorings

Um die SOP-Einflüsse des einfallenden Lichts auf die räumlichen Intensitätsverteilungen, insbesondere die Fokussierleistung, zu untersuchen, wurde das entworfene NRPL mit linear, zirkular, azimutal bzw. radial polarisiertem Licht beleuchtet. Alle Fälle wurden durch numerische FDTD-Simulationen berechnet. Gemäß der Matrixoptik können die unterschiedlich polarisierten Lichter durch die Jones-Matrixformalismen beschrieben werden, und der entsprechende Matrixausdruck wurde verwendet, um das einfallende Licht zu definieren. Die Grenze des Modells war eine perfekt angepasste Schicht (PML) mit einer Schichtnummer von 12. Um die Rechengenauigkeit und den Speicherverbrauch in den Simulationen auszugleichen, wurde die Maschengröße auf 10 nm im Ausgabebereich und 5 nm um den Fokusregion.

Ergebnisse

I Lineare Polarisation

Für das linear polarisierte Licht ist der SOP räumlich homogen, und in diesem Fall ist die Richtung des elektrischen Vektors parallel zum x Achse. Wenn das Licht den NRPL beleuchtet, existieren zwei Brennpunkte, die sich im gesamten elektrischen Feld 400 nm voneinander entfernt verteilen |E | ² wie in Abb. 3 dargestellt. Obwohl die Halbwertsbreiten (FWHMs) von beiden 210 nm betragen (~0,32 λ ₀ ) in der Brennebene zeigt das Simulationsergebnis, dass sich die Intensitätsverteilung offensichtlich von dem Design unterscheidet, das auf der Wellenfront-Rekonstruktionstheorie basiert, bei der ein kreisförmiger Fokus genau auf dem z . vorhanden sein sollte Achse (auch optische Achse genannt).

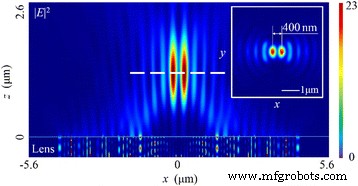
Intensitätsverteilungsmuster des gesamten elektrischen Felds |E | ² bei linear polarisiertem einfallendem Licht. Der Einschub zeigt das Intensitätsmuster in der Fokusebene. Die Brennweite beträgt 1215 nm (eine Abweichung von 6,54%). Die FWHMs beider Schwerpunkte sind ~0.32 λ ₀ , mit 400 nm voneinander entfernt und die Tiefenschärfe (DOF) beträgt ~1,68 λ ₀

Um die Unterschiede zwischen Simulation und theoretischem Design zu analysieren, werden die Intensitätsverteilungen der elektrischen Feldkomponenten untersucht. Wie in Abb. 4 dargestellt, erscheint ein elliptischer Fokus und die FWHM in x- und y- Richtung ist 220 nm (~0.34 λ ₀ ) und 457 nm (~0,70 λ ₀ ), bzw. Dieses Muster stimmt gut mit den experimentellen Ergebnissen von Lit. überein. [18] wo das gleiche polarisierte Licht angewendet wurde. Die Simulation zeigt jedoch, dass das Verteilungsmuster von |E | ² ähnelt dem Muster der Längskomponente |E _z | ² das 79,8 % der gesamten elektrischen Energie einnimmt. Daher wird der Unterschied hauptsächlich auf die außergewöhnliche Verteilung von |E . zurückgeführt _z | ² .

Intensitätsverteilung der transversalen Komponente |E _r | ² in der Brennebene. Der Einschub zeigt den elliptischen Fokus. Die Brennweite beträgt 1425 nm (eine Abweichung von 9,62 %). |E _r | ² nimmt 20,2% der gesamten elektrischen Energie ein. Der DOF beträgt ~1.41 λ ₀

Dieses Phänomen lässt sich letztendlich durch die Transmissionseigenschaft des NRPL erklären. Einerseits hängt die Anregung von SPPs an den Grenzflächen von Metall und Dielektrikum im Allgemeinen von der lokalen Polarisationsrichtung des einfallenden Lichts ab. Die transversalen elektrischen (TE) Wellen können nicht zur Anregung beitragen. Andererseits können sich aufgrund der Subwellenlängenstruktur des MIM-Wellenleiters nur die SP-Wellen durch diese Linse ausbreiten [32]. Mit der Rotationssymmetrie der Linse ändert sich die lokale transversale magnetische (TM) Komponente mit dem Azimutwinkel θ in der Kosinoidform. Daher ist, wie in Fig. 5a gezeigt, die Intensitätsverteilung von |E | ² , das sich knapp über der Endfläche der Linse befindet, konzentriert sich in der Nähe von y = 0 Bereich (−π/4 < θ < π/4). Dementsprechend breiten sich die Poynting-Vektoren entlang der radialen Richtung an der Endfläche aus, wie in Fig. 5b dargestellt. Somit ist die Vektorrichtung von E ist im Wesentlichen parallel zur optischen Achse, die den Hauptinhalt von E . bildet _z . Aufgrund der symmetrisch konstruktiven Interferenz treten in der Brennebene zwei Brennpunkte anstelle eines kreisförmigen Brennpunkts auf.

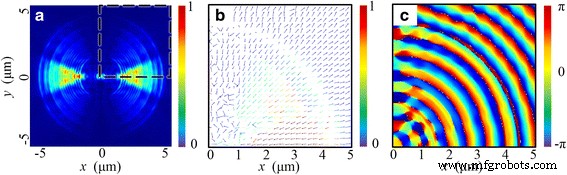
Die elektrischen Feldverteilungseigenschaften im Querschnitt nur 50 nm über der Endfläche der Linse. a Normalisierte Intensitätsverteilung von |E | ² . b Die Poynting-Vektorverteilung innerhalb der gestrichelten Linie Region in a. c Die entsprechende Phasenverteilung von E _z

II Zirkulare Polarisation

Da sich der Zustand von zirkular polarisiertem Licht mit der Zeit periodisch ändert, sind die simulierten Ergebnisse die zeitlich gemittelte Feldverteilung. Wenn die Linse von diesem polarisierten Licht beleuchtet wird, bildet sich in |E . ein ringförmiger Fokus _z | ² . Wie in Fig. 6a gezeigt, beträgt die Brennweite in diesem Feld 1185 nm, was eine Abweichung von 8,85 % vom Designwert ergibt. Die Breite des Donuts beträgt 210 nm (~0.32 λ ₀ ) und der Radius beträgt 400 nm. Die Schärfentiefe (DOF) beträgt ~1,65 λ ₀ . Das Gewicht von |E _z | ² 80,6 % der gesamten elektrischen Energie ausmacht. Außerdem in |E _r | ² , erzeugt die Überlagerung im Ortsbereich einen kreisförmigen Fokus mit der Brennweite von 1405 nm (eine Abweichung von 8,08%). Die FWHM beträgt 295 nm (~0,45 λ ₀ ) in diesem Feld und der DOF beträgt ~1.68 λ ₀ . Außerdem sind beide Verteilungsmuster in r-z Ebene ähneln denen im x -z Ebene bei linear polarisiertem Lichteinfall. Unter Berücksichtigung der radialen elektrischen Feldkomponente kann die FWHM auf 222 nm reduziert werden (~0,34 λ ₀ ).

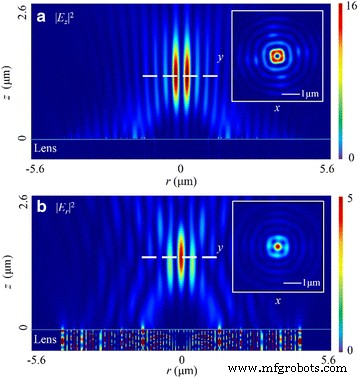
Intensitätsverteilungsmuster von |E _z | ² und |E _r | ² in r-z Ebene bei zirkular polarisiertem Licht. a In |E _z | ² , FWHM, DOF und Brennweite sind ~0.32 λ ₀ , ~1.65 λ ₀ , bzw. 1185 nm. b In |E _r | ² , FWHM, DOF und Brennweite sind ~0,45 λ ₀ , ~1.68 λ ₀ , bzw. 1405 nm

III Azimutale Polarisation

Für das azimutal polarisierte einfallende Licht stehen die elektrischen Vektoren senkrecht zur radialen Richtung, die parallel zur Gold/Vakuum-Grenzfläche des NRPL verlaufen. Da das azimutal polarisierte Licht die Linse beleuchtet, können die lokalen TE-Wellen die SPPs an der Grenzfläche nicht erregen. Somit ist die Transmissionsdistanz in Nanoringen proportional zu ihrer Breite, wie in Abb. 7 dargestellt. Da sowohl die Struktur als auch die Beleuchtung rotationssymmetrisch sind, wird nur die Hälfte des Intensitätsverteilungsmusters und die Struktur des NRPL gezeigt. Das durchgelassene Licht kann vernachlässigt werden und es gibt keinen deutlichen Fokus im Ausgabebereich.

Intensitätsverteilungsmuster im Linsenbereich und seine Querschnittsansicht. Die Übertragungsdistanz der Nicht-SP-Wellen in Nanoringen ist proportional zur Spaltbreite

IV Radiale Polarisation

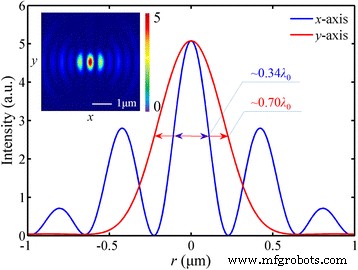
Entsprechend dem azimutal polarisierten Licht kann das radial polarisierte Licht als lokale TM-Welle betrachtet werden, und diese Polarisationseigenschaft entspricht der Anregungsbedingung von SPPs, was zu einer höheren maximalen Intensität im Fokus beiträgt. Im gesamten elektrischen Feld E , ist die maximale Intensität fünfmal größer als die für das linear polarisierte einfallende Licht. Darüber hinaus gibt es einen kreisförmigen Fokus mit dem 276-nm (~0,42 λ ₀ ) FWHM in |E | ² , wie in Abb. 8 gezeigt. Die simulierte Intensitätsverteilung ist der Fokussierungsfähigkeit der refraktiven Linse mit hoher NA sehr ähnlich [33]. Darüber hinaus hängt diese Fokussierungsleistung immer noch von |E . ab _z | ² , das 82,0 % der gesamten elektrischen Energie ausmacht.

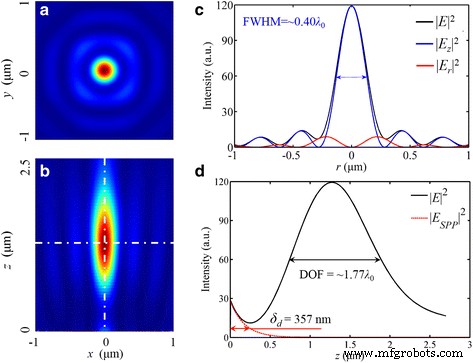
Intensitätsverteilung von |E | ² bei radial polarisiertem einfallendem Licht. a , b Die Verteilung in der Brennebene und die in x -z Kreuzung. c Das Intensitätsprofil in radialer Richtung. d Das Intensitätsprofil entlang der optischen Achse, wo die schwarze durchgezogene Linie ist die gesamte Verteilung der elektrischen Feldstärke in der Simulation und die rote gestrichelte Linie ist die berechnete Kurve von SPP. Die Brennweite beträgt 1275 nm (eine Abweichung von 1,92%). Die FWHM von |E | ² und |E _z | ² beträgt 272 nm (~0,42 λ ₀ ) und 260 nm (~0,40 λ ₀ ), bzw. Der DOF beträgt ~1,77 λ ₀

Anders als in den vorherigen Fällen gibt es in |E . einen kreisförmigen Fokus _z | ² . Außerdem bestimmt diese Komponente auch das Verteilungsmuster in |E | ² . Wie in Abb. 9a dargestellt, ist die FWHM in |E _z | ² beträgt 260 nm (~0,40 λ ₀ ), die im Fall von Nanoschlitz-basierter PL nahe der Brennlinie liegt [16]. Insbesondere beträgt die Brennweite 1275 nm. Verglichen mit dem entworfenen Wert verringert sich der relative Fehler auf 1,9 %. Die Brennweite beträgt jedoch 1455 nm (eine Abweichung von 11,2%) in |E _r | ² . Wie in Abb. 9b dargestellt, gibt es einen ringförmigen Fokus mit einer Breite von 227 nm (~0,35 λ ₀ ) in diesem Bereich. Der DOF beträgt ~1,60 λ ₀ .

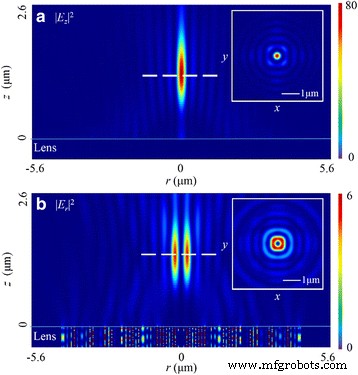
Intensitätsverteilungsmuster von |E _z | ² und |E _r | ² in r-z Ebene bei radial polarisiertem Licht. a |E _z | ² Muster im r-z Flugzeug. Der Einschub zeigt einen kreisförmigen Fokus in der Fokusebene. b Das quere |E _r | ² Muster im r-z Flugzeug. Der Einschub zeigt einen ringförmigen Fokus in der Fokusebene

Die Phasenverzögerung der SP-Wellen in Nanoringen wird untersucht, wie in Abb. 10 dargestellt. Die Simulation zeigt, dass die Phasenmodulation dramatisch von den strukturellen Parametern der NRPL beeinflusst wird und die simulierten Phasenverzögerungen zwischen der Einfallsfläche und der Austrittsfläche sind im Wesentlichen identisch mit den berechneten Werten nach Gl. (2). An der Stirnfläche der Linse breiten sich die SP-Wellen immer noch in radialer Richtung aus und in der Mitte der Fläche befindet sich ein Hotspot, dessen Intensität ein Fünftel der Fokusintensität beträgt. Die konstruktive Interferenz der SP-Wellen mit der rotationssymmetrischen Verteilung konstruiert die sich ausbreitenden Wellen und realisiert den kreisförmigen Fokus im Quasi-Fernfeld.

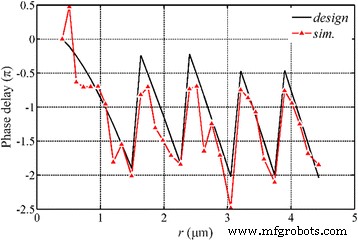
Phasenanalyse des NRPL unter dem radial polarisierten Einfallslicht

Diskussionen

I Superfokussierfähigkeit von NRPLs

Da das einfallende Licht mit unterschiedlichen SOPs verwendet wird, einschließlich der linearen, zirkularen und radialen Polarisation, können die Subbeugungsgrenzfokusse realisiert werden. Obwohl die Brennpunktform durch die SOP beeinflusst wird, überwinden die charakteristischen Größen dieser Brennpunkte alle die Rayleigh-Beugungsgrenze (413 nm). Die Simulationsergebnisse demonstrieren erfolgreich die Superfokussierfähigkeit des NRPL, und die Intensitätsverteilung in der Fokusebene ähnelt der Bessel-Funktion, die verwendet wird, um den nicht beugenden Strahl zu beschreiben.

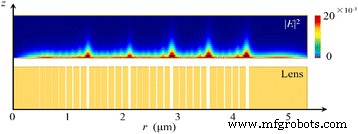
Für den Fall des radial polarisierten einfallenden Lichts, als Beispiel in Fig. 11, ist die Intensitätsverteilung in |E _z | ² ist identisch mit der Bessel-Funktion nullter Ordnung J ₀ (K _spp ⋅ n ⋅ r ), wobei n und r ist der Brechungsindex des Umgebungsmediums bzw. der radiale Abstand zur optischen Achse. Die FWHM des Fokus ist etwas größer als die mit J calculated berechnete Größe der Hauptkeule ₀ . Insbesondere zeigen die Simulationen, dass der nicht beugende Strahl im Quasi-Fernfeld realisiert werden kann. Die SP-Wellen nehmen als eine Art evaneszente Welle exponentiell ab, wenn sie sich von der Austrittsfläche weg ausbreiten, und die Ausbreitungsstrecke im Vakuum kann berechnet werden nach [30]:

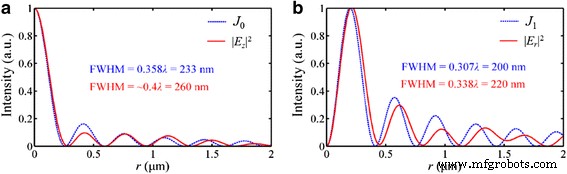
Intensitätsprofile der NRPL in der Brennebene unter dem radial polarisierten einfallenden Licht. a Die Verteilung von |E _z | ² ähnelt der Bessel-Funktion nullter Ordnung J ₀ . b Die Verteilung von |E _r | ² ähnelt der Bessel-Funktion erster Ordnung J ₁

wo ε _d und ε _m sind die Permittivität von Dielektrikum bzw. Metall. Also, δ _d beträgt 357 nm, was mit der in Fig. 8d gezeigten Simulation übereinstimmt. Daher kann die Intensität der SP-Wellen im Fokus im Quasi-Fernfeldbereich vernachlässigt werden.

II Fokusform

Durch Modulieren des SOP können die elliptischen, kreisförmigen und ringförmigen Brennpunkte in der Brennebene realisiert werden, wie in Abb. 12 dargestellt. Das Phänomen wird der Subwellenlängen-Brennweite zugeschrieben, und wir können den kreisförmigen Typ nicht realisieren Fokus in elektrischen und magnetischen Feldern gleichzeitig. Somit wird in den magnetischen (oder elektrischen) Feldern ein Fokus vom Donuttyp realisiert, während im entsprechenden elektrischen (oder magnetischen) Feld ein kreisförmiger Fokus erreicht wird. Da insbesondere kein longitudinales Magnetfeld vorhanden ist, ist die Intensitätsverteilung von |H | ² ist das gleiche wie das Muster von |E _r | ² . Außerdem |E _z | ² nimmt etwa 80,0 % der gesamten elektrischen Energie ein und die Skala wird nicht durch die SOPs des einfallenden Lichts beeinflusst.

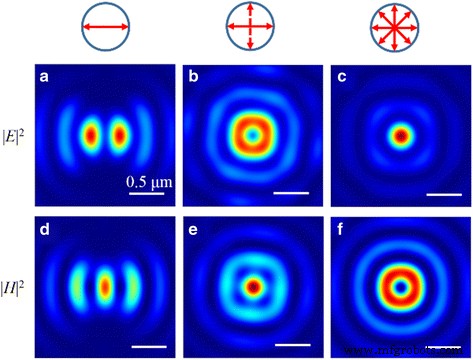
Die normalisierten Intensitätsmuster des elektrischen Felds |E | ² und Magnetfeld |H | ² in der Brennebene, wenn die NRPL durch das polarisierte Licht beleuchtet wird. a |E | ² und d |H | ² Verteilung mit linear polarisiertem Auflicht. b |E | ² und e |H | ² Verteilung mit zirkular polarisiertem Auflicht. c |E | ² und f |H | ² Verteilung mit radial polarisiertem Auflicht

III Brennweitenmodulation

Die simulierte Brennweite liegt in verschiedenen Fällen im Wesentlichen nahe der gewünschten Position f ₀ (1300 nm), wie in Tabelle 1 gezeigt. Wir erkennen jedoch, dass die Brennweite im transversalen Feld |E _r | ² ist etwa 200 nm länger als im Längsfeld |E _z | ² , unabhängig von der SOP des einfallenden Lichts und die Abweichung besteht üblicherweise.

Theoretisch ist die Wellenfront-Rekonstruktionstheorie geeignet, um die NRPL mit einer beliebigen Brennweite vom Nahfeld bis zum Fernfeld zu entwerfen. Ob die tatsächliche Brennweite einer konstruierten plasmonischen Linse jedoch gut mit der entworfenen Brennweite übereinstimmt, hängt von der Gesamtphasendifferenz der Linse ab. Die Abweichung kann auf die Unterscheidung zwischen dem Fokus vom Amplitudentyp und dem Fokus vom Phasentyp zurückzuführen sein [34]. Da die Phasenmodulation im MIM-Wellenleiter auf die radiale Komponente abzielt, ist die Brennweite in |E _r | ² kann durch die Wellenfront-Rekonstruktionstheorie moduliert werden, wenn die Gesamtphasendifferenz von mindestens 2π erfüllt ist [15]. Für die Längskomponente ist eine größere Gesamtphasendifferenz (> 10π) für die Konsistenz von Vorteil. Wie in Fig. 13 gezeigt, wenn die Phasendifferenz von 2π auf 16π zunimmt, entsprechend der NA von 0,75 auf 0,96, der Fokus vom Amplitudentyp in |E _z | ² moves from the output surface of the lens to the desired position. As the intensity distribution of |E | ² is decided by |E _z | ² , the NA can dramatically influence the focal length in the total electric field. However, the change of the focal length in |E _z | ² decreases gradually, along with the increase of the total phase difference. On the other hand, the position of the phase-type focus in |E _r | ² is relatively stable. When the NRPL with a high NA is applied, there is still a deviation in focal length derived based on the intensity distribution of |E _x | ² and |E _z | ² , and the deviation almost keeps invariable. Therefore, the focal length of the NRPLs can be effectively controlled by the phase modulation and structural optimization, though the same focal length cannot be achieved in the transverse and longitudinal component fields.

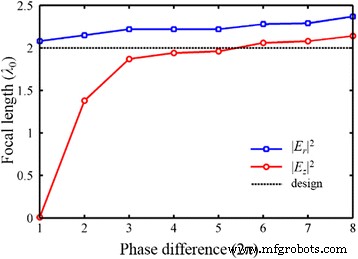
The focal length of the NRPL with the increase of total phase difference from 2π to 16π

IV Focusing Performace in the Non-Coaxial Situation

The non-coaxial situation is a common problem in the experiment, and its effect on the focusing performance should be considered. As shown in Fig. 14, the center of the radially polarized light deviates 3 μm from the optical axis of the NRPL along the x axis. Compared with Figs. 8 and 9, the intensity distributions both in x-z cross section and in focal plane are apparently changed. In the longitudinal electric field, an elliptical focus is located at 1340 nm away from the exit surface of the lens. The FWHMs in x-z and y-z planes are 0.51 and 0.38 λ ₀ , respectively. On the other hand, the distribution in transverse field is also distorted, where the intensity of one side lobe is higher than the other one. Furthermore, compared with the coaxial condition, the decrease of the maximum intensity in the total electric field is more than 85%.

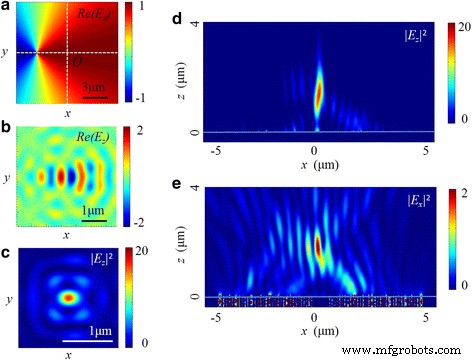
The intensity distribution of the NRPL in the non-coaxial situation. a The real part of E _x of radially polarized incident light. b , c The distribution of Re(E _z ) and |E _z | ² in the focal plane. d , e The distribution of |E _z | ² and |E _x | ² in the x-z plane

The preliminary simulation indicates that the non-coaxial situation indeed influences the intensity distribution and the desired focusing performance of lens. Therefore, it is essential to guarantee the coaxiality between the incident light and the lens center during the experiment.

Conclusions

In summary, we build a NRPL with a high NA utilizing the wavefront reconstruction theory and the dispersion relation of the MIM waveguide. We also investigate the polarization-dependent focusing performance in the quasi-far field, including the focal length, FWHM, DOF, and the maximum intensity. The conventional polarized light, such as the linearly, circularly, radially, and azimuthally polarized light, are all considered. The simulations demonstrate the superfocusing capability of the designed NRPL. Utilizing the polarization-dependent property, the sub-diffraction-limit elliptical-, circular-, and donut-shape foci can be realized. However, one limitation of this work is that the proposed design strategy to realize the superfocusing performance of NRPLs is aimed for the quasi-far-field region, although to the best of our knowledge, the similar focusing capability in this region is rarely reported. In addition, we discover the underlying physical phenomenon on the focal shift and propose a more effective way to control the focusing position by employing both the transverse and longitudinal fields. There are considerable engineering applications for the nanoring-based superfocusing lenses, ranging from the super-resolution imaging, particle acceleration, quantum optical information processing to the optical data storage.

Abbreviations

DOF:

Depth of focus

FDTD:

Finite-difference time-domain

FWHM:

Full-width at half maximum

MIM:

Metal-insulator-metal

NRPL:

Nanoring-based plasmonic lenses

PML:

Perfectly matched layer

SOP:

State of polarization

SPPs:

Surface plasmon polaritons

TE:

Transverse electric

TM:

Transverse magnetic