Effizientes und effektives Design von InP-Nanodrähten für maximale Sonnenenergiegewinnung

Hintergrund

Für Solarzellen der zukünftigen Generation haben Halbleiter-Nanodraht-Arrays (NW) einen neuen Weg gefunden, um den Materialverbrauch und die Herstellungskosten erheblich zu reduzieren und gleichzeitig die Geräteleistung im Vergleich zu ihren Dünnschicht- oder Bulk-Gegenstücken aufrechtzuerhalten oder sogar zu verbessern [1, 2]. Diese faszinierende Eigenschaft wird größtenteils den bemerkenswerten optischen Eigenschaften der NWs zugeschrieben, einschließlich erhöhter Absorption [3, 4] und spektraler Selektivität [5,6,7]. Unter verschiedenen III-V-Materialien haben InP-NW-Arrays aufgrund der direkten Bandlücke und der geringen intrinsischen Oberflächenrekombinationsgeschwindigkeit intensive Forschungsanstrengungen für Solarzellenanwendungen auf sich gezogen [8]. Bisher erreichte die höchste Energieumwandlungseffizienz 13,8% für InP-NW-Arrays in einer Zelle von 1 mm ² im Bereich [9].

Da die optischen Eigenschaften von NW-Arrays durch die Abstimmung ihrer dreidimensionalen Geometrie deutlich angepasst werden können, um die Leistung von NW-basierten Solarzellen weiter zu verbessern, wurde große Aufmerksamkeit auf die Optimierung der Morphologie und Topologie von III-V-NW-Arrays gelegt um die Lichtabsorption zu maximieren [5, 9,10,11,12,13]. Insbesondere der Durchmesser, die Periodizität und die Anordnung der NWs wurden untersucht, um die Absorption der Sonnenenergie zu maximieren [6, 14, 15, 16]. Es wird berichtet, dass das Einstellen des Durchmessers des NW die im NW vorhandenen optischen Moden ändert. Dies führt zu lokalisierten Lichtabsorptionsmaxima für die einfallenden Wellenlängen, die den jeweiligen Resonanzmoden entsprechen [5, 6, 17, 18]. Außerdem können NW-Arrays mit optimierter Periodizität oder optimiertem Füllverhältnis (FR) die Reflexion und Transmission unterdrücken und gleichzeitig die Streuung des einfallenden Lichts verbessern, was zu einem verlängerten optischen Weg und damit einer verbesserten Lichtabsorption führt [19,20,21]. Außerdem haben Martin Foldyna et al. kamen zu dem Schluss, dass die Abhängigkeit der Lichtabsorption von der Anordnung der NW-Arrays eher gering ist, da der Lichteinfangeffekt von NWs auf der individuellen Wellenleitung beruht, wenn die Lichtkopplung zwischen benachbarten NWs vernachlässigt wird [22].

Um die maximale Sonnenenergieernte zu finden, sollten die Wirkung der dreidimensionalen Parameter und die Anordnung der NW-Arrays gemeinsam betrachtet werden. Die meisten der berichteten optimalen geometrischen Abmessungen und Anordnung von NW-Arrays für eine maximale Sonnenspektrum-Ernte sind jedoch immer noch Parameterraum-bestimmte lokale Optima. Außerdem erschweren das einfallende Sonnenspektrum in Kombination mit den Materialdispersionseigenschaften die analytische Lösung dieses Problems. Daher werden häufig intensive und zeitaufwendige numerische Simulationen wie die Finite-Differenz-Zeitdomäne (FDTD) verwendet, um dieses Multiparameter-Optimierungsproblem anzugehen. Sturmberget al. berichteten über eine semianalytische Methode, um den Bereich der optimalen Abmessungen von NW-Arrays mit einem einzigen Durchmesser einzugrenzen [13]. Obwohl diese Methode für verschiedene Materialien anwendbar ist, sollten FDTD-Simulationen dennoch begleitet werden, um die genauen optimalen Werte zu finden. Darüber hinaus ist diese Methode für hervorragende Absorber in Kombination mit NW-Arrays mit mehreren Radien weniger hilfreich [23].

In diesem Papier präsentieren wir ein analytisches Design für optimale geometrische Abmessungen von InP-NW-Arrays mit einfachem, doppeltem und mehrfachem Durchmesser, um die Sonnenenergieabsorption zu maximieren. Die Durchmesser von NWs werden durch die Leaky-Mode-Resonanz und die Mie-Theorie bestimmt, während die Periodizitäten durch den Aufbau einer effektiven Mediumschicht identifiziert werden, um die Lichtreflexion und -transmission zu minimieren. Es werden sowohl quadratisch als auch hexagonal verteilte NW-Arrays betrachtet. Darüber hinaus werden intensive FDTD-Simulationen begleitet, um die Wirksamkeit unserer Methode zu überprüfen. Die gute Anpassung der größten Kurzschlussstromdichten, die von den NW-Arrays erzeugt werden, mit den berechneten geometrischen Parametern und den Werten, die aus FDTD-Simulationen erhalten wurden, beweisen die Wirksamkeit der vorgeschlagenen Methode, um das praktische NW-basierte Design von Photovoltaikzellen zu leiten.

Design für maximales Light Harvesting von InP-NWs

Vertikal ausgerichtete InP-NW-Arrays werden auf einem semi-unendlichen SiO₂ . platziert Substrat, wie in Fig. 1 schematisch gezeigt, entweder mit quadratischer oder hexagonaler Anordnung. Wiederholbare Elementarzellen in den Einfügungen der Fig. 1a, b erläutern die jeweiligen Charakterisierungsdimensionen für jede Anordnung. Diese Morphologie und Topologie der NW-Arrays stimmt mit der Mehrzahl der InP-NW-basierten Solarzellenstrukturen überein [11, 12, 23, 24]. Innerhalb jeder der Elementarzellen haben die NWs den gleichen oder unterschiedliche Durchmesser wie D _ich . Periodizität p ist als der Mitte-zu-Mitte-Abstand eines Paares benachbarter NWs definiert, der den gleichen Wert für quadratisch angeordnete NWs hat, während unterschiedliche Werte für hexagonale NW-Anordnungen. Dementsprechend ist die FR der quadratisch angeordneten NW-Arrays definiert als \( \pi {\sum}_{\mathrm{i}=1}^4{D_i}^2/{(4p)}^2 \) mit dem Maximalwert von π/4 wenn die NWs den größten Volumenprozentsatz der Elementarzelle einnehmen [25]. In ähnlicher Weise ist die FR für hexagonale NW-Arrays definiert als \( \pi {\sum}_{\mathrm{i}=1}^2{D_i}^2/\left(4\sqrt{3}{p}^ 2\right)\) mit dem maximalen Wert von \(\pi\sqrt{3}/6\) [22]. Die Länge l des NW wird für alle Fälle auf 2 μm festgelegt, da sie lang genug sind, um bei richtiger Auslegung mehr als 90 % der einfallenden Energie zu absorbieren [26].

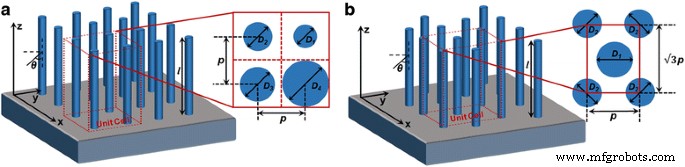
Schemata von vertikal ausgerichteten InP-NW-Arrays. a Quadratisch und b hexagonale NW-Arrays mit Einfügungen, die ihre jeweiligen Elementarzellen erklären

Um jeden geometrischen Parameter von NW-Arrays analytisch zu bestimmen, wird das Mehrparameter-Optimierungsproblem für maximales Lichtsammeln in zwei Prozesse zerlegt:(1) durchmesserbestimmende Resonanzmodussteuerung der NWs und (2) FR-beeinflusste minimale Reflexion und Transmission der einfallenden Sonnenenergie. Wir konstruieren die Beziehung einzelner geometrischer Parameter mit dem jeweiligen Determinantenprozess und identifizieren jeden optimalen Wert, der zu einer maximalen Lichtabsorption führt. Als Konstruktionsbeispiel zur Veranschaulichung des vorgeschlagenen Verfahrens werden NW-Arrays mit doppeltem Durchmesser gewählt. Optimale geometrische Abmessungen von NW-Arrays mit einem einzigen Durchmesser als einfacherer Fall können auch während der Ableitung erfasst werden. Als Erweiterung des Beispiels können auch der Durchmesser und die Periodizität für NW-Arrays mit vier Durchmessern berechnet werden. Für quadratisch angeordnete NW-Arrays mit doppeltem Durchmesser haben die Durchmesser der diagonalen NWs den gleichen Wert wie D _Hauptfach und die Durchmesser der restlichen zwei NWs werden als D . bezeichnet _zusätzlich . Bei hexagonal angeordneten NW-Arrays beträgt der Durchmesser des mittleren NW D _Hauptfach und die Durchmesser der NWs an der Peripherie sind D _zusätzlich .

Es wird berichtet, dass NW-Arrays undichte/geführte Resonanzmoden unterstützen können, die jeweils zu starken Absorptionspeaks führen. Außerdem legt die grundlegende Natur des Wellenleiters nahe, dass die Modenzahl mit dem Anstieg des Durchmessers von NW wächst. Folglich sollte der optimale Durchmesser von NW groß genug sein, um mehr Moden zu unterstützen, um eine größere Anzahl von Absorptionsresonanzen einzuschließen. Zu große Durchmesser von NWs sind jedoch weniger bevorzugt, da die von ihnen unterstützten Moden höherer Ordnung mehr Knoten besitzen, die weniger effizient an die einfallenden ebenen Wellen koppeln [13]. Daneben setzen die Materialeigenschaft und das einfallende Sonnenspektrum der Auswahl des optimalen Durchmessers weitere Grenzen. Nur wenn die Resonanzmoden innerhalb des Absorptionsbereichs liegen, können sie zum Photostrom beitragen. Der Absorptionsbereich wird durch die Überlagerung des Absorptionsbereichs des Materials bis zur kritischen Wellenlänge und des einfallenden AM 1,5G-Spektrums definiert [27].

Um das D . quantitativ zu bestimmen, _Hauptfach der NW-Arrays wird zunächst die Leaky-Mode-Resonanz verwendet, um die jeweiligen Resonanzwellenlängen für verschiedene Durchmesser von NWs zu berechnen [2]. Daraus ergibt sich die Verteilung der Resonanzmoden im Absorptionsbereich. Daher ist das optimale D _Hauptfach sollte zwei Modi unterstützen, um alle oben genannten Kriterien zu erfüllen. Zweitens wird die Mie-Theorie verwendet, um die normalisierten Absorptionseffizienzen dieser NWs in Schritt eins zu berechnen. Streng genommen kann die Mie-Theorie nicht auf Situationen angewendet werden, in denen der einfallende Wellenvektor perfekt parallel zur Achse der NWs ausgerichtet ist, da die Eigenwertgleichung schlecht definiert ist [28]. Diese Situation kann jedoch angenähert werden als Verglasungseinfall von einfallendem Licht (sehr kleiner Einfallswinkel θ in Bezug auf die NW-Achse), da an der Grenzfläche von NW-Arrays die Wellenfront des einfallenden Lichts durch den hohen Index von NWs gestört wird, der transversale Komponenten in den Wellenvektor einführt, was die Übernahme der Mie-Theorie ermöglicht [18]. Daher ist das optimale D _Hauptfach sind diejenigen, die zwei Moden unterstützen, während sie die Halbwertsbreite (FWHM) der niedrigsten Resonanzmode im normalisierten Absorptionseffizienzspektrum innerhalb des Absorptionsbereichs halten. Nach Erwerb von D _Hauptfach , das D _zusätzlich wird unter der Bedingung berechnet, dass die NWs eine Mode zur Reduzierung von Reflexion und Materialeinsparung unterstützen sollten und ihre Resonanzwellenlänge sollte dem Tal des D . entsprechen _Hauptfach s normalisiertes Absorptionseffizienzspektrum.

Die Periodizität der NW-Arrays kann durch den Aufbau einer effektiven Mediumschicht berechnet werden. Diese künstliche Schicht stellt das Reflexions- und Transmissionsverhalten der NW-Arrays dar, das sich nur auf das Material FR bezieht. Dadurch werden Durchmesser, Periodizität und Anordnung der NW-Arrays aus der Berechnung herausgenommen. Auf diese Weise können die Transmission und das Reflexionsvermögen von NW-Arrays durch Anwendung von Fresnel-Gleichungen auf diese effektive Mediumschicht bewertet und somit der optimale FR analysiert werden. Basierend auf der Beziehung von FR und Periodizität werden die Periodizitäten sowohl für hexagonal als auch für quadratisch angeordnete NW-Arrays erhalten. Eine detaillierte Beschreibung unserer vorgeschlagenen Methode finden Sie in den folgenden Abschnitten.

A. Optimale Durchmesser von InP-NW-Arrays für maximales Lichtsammeln

Um die Lichtabsorption zu erhöhen, sollte die Anzahl der Resonanzmoden, die zu starken Absorptionspeaks führen, innerhalb des Absorptionsbereichs maximiert werden. Am blauen Ende des Absorptionsbereichs begrenzt das einfallende AM 1,5 G-Spektrum 300 nm als Hochenergiebereich. Die kritische Wellenlänge λ _c von 925 nm (Bandlücke von InP 1,34 eV) begrenzt das rote Ende des Absorptionsbereichs. Als Ergebnis wird bewiesen, dass die InP-NWs, die zwei Resonanzmoden unterstützen, die sich innerhalb des absorbierenden Bereichs befinden, die Lichtabsorption am besten verbessern können [29]. Wir erweitern diese Schlussfolgerung und verwenden die Mie-Theorie, um den genauen Wert zu berechnen.

Gemäß der obigen Schlussfolgerung ist der Bereich von D _Hauptfach kann aus der aus den Maxwell-Gleichungen abgeleiteten Eigenwertgleichung berechnet werden [18]. Unter Berücksichtigung der antisymmetrischen Feldverteilung in der Ebene der einfallenden ebenen Wellen ist nur der HE_1m Moden können effektiv angeregt werden, um zur Absorption von vertikal ausgerichteten NWs beizutragen [5]. Diese HE_1 m Moden erfüllen die Eigenwertgleichung, und die Resonanzwellenlängen können unter der Annahme erhalten werden, dass der Realteil der Ausbreitungskonstante Re(β _z ) der Mode entlang der NW-Achsenrichtung gegen Null geht, wie in Gl. (1). k _Zyl und k _Luft sind die transversalen Komponenten des Wellenvektors innerhalb der NWs und in der Luft, während ε _Zyl und ε _Luft sind die jeweiligen Zulassungen. J ₁ und H ₁ ⁽¹⁾ sind die Bessel- und Hankel-Funktionen erster Art erster Art. Folglich kann der Bereich, in den der Primärdurchmesser fällt, unter der Bedingung empfangen werden, dass die entsprechende HE₁₁ und HE₁₂ Mode innerhalb des absorbierenden Bereichs liegen.

Nach der Mie-Theorie beträgt die Absorptionseffizienz Q _Bauchmuskeln der NWs wird durch das Verhältnis der Energiesammelfläche und der geometrischen Größe der NWs definiert. Der analytische Ausdruck der Absorptionseffizienz Q _Bauchmuskeln ist unten angegeben, und der genaue mathematische Formalismus der Mie-Theorie kann in der Referenz [30] gefunden werden. Dabei ist \( \overline{n}=n+ ik \) der komplexe Brechungsindex; wie oben erwähnt, J _ich und H _ich ⁽¹⁾ sind die Bessel- und Hankel-Funktionen erster Ordnung i .

Nach dem Erwerb das Q _Bauchmuskeln der HE₁₁ Modus kann die FWHM des jeweiligen Durchmessers von NWs ermittelt werden, und daher wird der optimale Durchmesser für maximales Lichtsammeln bestimmt. Bei der Entscheidung über den Hauptdurchmesser wird der Zusatzdurchmesser unter der Bedingung bestätigt, dass seine normalisierte Absorptionspeakwellenlänge mit dem normalisierten Absorptionseffizienztal des Hauptdurchmessers übereinstimmen sollte. Für NW-Arrays mit vier Durchmessern werden der dritte und vierte Durchmesser auf ähnliche Weise bestimmt. Ihre normalisierten Absorptionseffizienzpeaks sollten mit den Tälern der Überlagerung des normalisierten Absorptionseffizienzspektrums der primären und sekundären NWs übereinstimmen. Es ist bemerkenswert, dass mit Ausnahme der Haupt-NWs der zweite, dritte und vierte NW nur ​​eine Mode unterstützen sollen, da die Größe des kleinen Durchmessers sowohl das Reflexionsvermögen an der Luft-NW-Grenzfläche als auch den Materialverbrauch reduzieren kann.

B. Optimaler FR von InP-NW-Arrays für maximales Lichtsammeln

Verschiedene veröffentlichte Arbeiten haben dies mit festen Durchmessern von NWs offenbart; die Absorption der NWs wird anfangs mit der FR zunehmen und dann nach einem bestimmten optimalen Wert sinken [13]. Der Anstieg der Lichtabsorption wird normalerweise auf die Zunahme des Volumenanteils der Halbleitermaterialien mit hohen Absorptionskoeffizienten zurückgeführt. Wenn FR weiter anwächst, nimmt der durchschnittliche Brechungsindex der NW-Anordnungen zu und somit steigt die Reflexion, was die Lichtabsorption verringert. Daher sollte eine Obergrenze für den FR gefunden werden, um den Einfluss der Fresnel-Reflexion und -Transmission zu optimieren, um die Absorption der NW-Arrays zu maximieren. Abbildung 2 veranschaulicht schematisch, dass eine effektive Mediumschicht mit komplexem Brechungsindex erstellt wird, um das Brechungs- und Transmissionsverhalten der NW-Arrays darzustellen. Auf diese Weise werden die Periodizitäten und Durchmesser von NWs aus der Berechnung herausgenommen. Folglich kann eine Fresnel-Berechnung der Reflexion und Transmission der effektiven Mediumschicht verwendet werden, um die Eigenschaften der NW-Arrays widerzuspiegeln. Die genaue Beschaffenheit innerhalb dieser künstlichen Mediumschicht wird nicht berücksichtigt, solange sie die Reflexion und Transmission von NW-Arrays darstellen kann. Detaillierte mathematische Ableitungen sind unten angegeben.

Lichtreflexion, Transmission und Absorption von NWs und effektiver Mediumschicht. a InP NW-Arrays und b die entsprechende wirksame Mittelschicht mit der gleichen Dicke

Der Realteil des Brechungsindex der effektiven Mediumschicht n _{em_real} werden durch die Bruggeman-Formulierung [31] in Gl. (4) wobei Ɛ_em , und Ɛ_NW sind die Permittivität der effektiven Mediumschicht bzw. InP. Der Imaginärteil des Brechungsindex n _{em_imag} wird durch Volume Averaging Theory [32, 33] in Gl. (5) wobei die n _{NW_real} , n _{NW_imag} , n _{air_real} , und n _{air_imag} sind der Real- und Imaginärteil des Brechungsindex von NW und Luft. Die optimale FR_opt ist als FR definiert, so dass Absorption Abs(λ) = 1 − R(λ) − T(λ) wird mit Fresnel-Gleichungen maximiert.

Durch Ersetzen der NW-Arrays durch einen dünnen Film gleicher Dicke wird der Reflexionsgrad R(λ) und T(λ) Transmission von NW-Arrays kann unter Verwendung der Fresnel-Gleichungen geschätzt werden. Die ersten beiden Terme der unendlichen Fabry-Perot-Reflexions- und Transmissionsreihen sind in Abb. 2b enthalten. Detaillierte mathematische Herleitungen finden sich auch in den Begleitinformationen der Literaturstelle [13]. In diesem Stadium werden sowohl die optimalen Durchmesser als auch die FR bestimmt und die entsprechende Periodizität kann basierend auf der Definition der FR ermittelt werden. Bei optimalen geometrischen Abmessungen sollten die NW-Arrays zu maximaler Lichtabsorption führen. Kurzschlussstromdichte J _sc wird meistens verwendet, um die Lichtsammelfähigkeit zu messen, wobei angenommen wird, dass jedes absorbierte Photon zu einer Exzitonentrennung gefolgt von einer erfolgreichen Ladungsträgersammlung führt. Die Definition ist in Gl. (6) wobei A(λ) ist die Absorption innerhalb von Nanodrähten als Funktion der einfallenden Wellenlänge und N(λ) ist die Anzahl der Photonen pro Flächeneinheit pro Sekunde für die einfallende Wellenlänge aus dem Standard-Sonnenspektrum.

Ergebnisse und Diskussion

Einzel- und Mehrfachdurchmesser von InP-NW-Arrays mit quadratischen und hexagonalen Anordnungen demonstrieren die Gültigkeit der vorgeschlagenen Methode. Inzwischen werden auch numerische FDTD-Simulationen (Lumerical FDTD Solutions 8.15) zum Vergleich mit unserer Methode angeboten. Periodische Randbedingung wird entlang x . angewendet und y Achsen, während eine perfekte Übereinstimmungsbedingung entlang z . festgelegt ist Achse wie in Abb. 1 dargestellt. Die InP-NWs stehen vertikal auf SiO₂ Substrat. Die optischen Konstanten für InP und SiO₂ stammen aus Palik-Materialdaten von Lumerical. Der Parameterraum für Durchmesser von NWs reicht von 50 bis 200 nm, während der FR von 0,05 bis zu den möglichen Maximalwerten für quadratische und hexagonale NWs reicht.

A. Maximales Lichtsammeln für InP-NWs mit einem einzigen Durchmesser

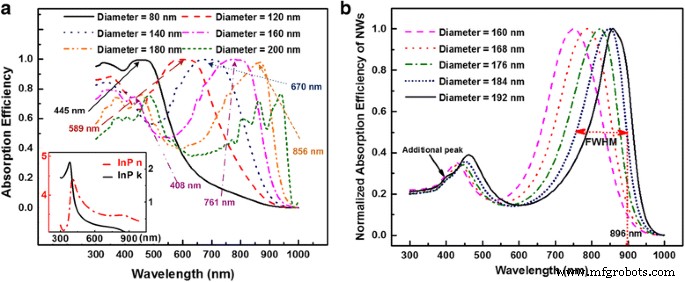
Abbildung 3a zeigt die Lichtabsorptionseffizienz für InP-NW-Arrays mit einem einzigen Durchmesser, wenn FR 0,05 beträgt, wobei die optischen Konstanten im Einschub angegeben sind. Die jeweiligen Resonanzwellenlängen werden berechnet und auf entsprechenden Absorptionspeaks markiert, die gut mit den FDTD-Simulationsergebnissen übereinstimmen. Die Rotverschiebung von HE₁₁ Resonanzmode kann leicht mit der Zunahme des Durchmessers von NWs beobachtet werden. Außerdem beweisen sowohl Berechnung als auch Simulation, dass sich die Resonanzmode von einer zu zwei Moden bei 140 nm Durchmesser entwickelt. Daher sollte der optimale Wert für die maximale Lichtabsorption größer als 140 nm und kleiner als 200 nm sein, wenn zwei Moden in jedem NW angeregt werden. Um den optimalen Durchmesserwert zu finden, wird in Fig. 3b eine normalisierte Absorptionseffizienz von NW-Arrays bereitgestellt, die die NW-Arrays zeigt, die zwei Moden unterstützen und die FWHM immer noch innerhalb des absorbierenden Bereichs halten. Daher wird der größte Wert von 184 nm Durchmesser als optimaler Durchmesser ohne zusätzliche Spitze gewählt. Interessanterweise hat das aktuelle InP-NW-Solarzellendesign mit dem höchsten Leistungsumwandlungswirkungsgrad den optimalen Durchmesser von 180 nm angenommen. Ihre Durchmesser der NWs wurden experimentell im Bereich von 50 bis 300 nm mit 10 nm als Erhöhungsschritt optimiert [9]. Im Vergleich zu unserer Vorhersage von 184 nm zeigt eine enge Toleranz von 4 nm die Genauigkeit unserer Methode.

Wellenlängenabhängige Absorptionseffizienz von InP-NWs und normalisierte Absorptionseffizienz. a Absorptionseffizienz von NWs mit Einschub zur Erklärung der optischen Konstanten. b Berechnete Absorptionseffizienz nach Mie-Theorie

Der Füllgrad wird analytisch unter Verwendung der wirksamen Mediumschicht in Abschnitt B des beschriebenen Verfahrens erhalten. Die Lichtabsorptionseffizienz der effektiven Schicht mit derselben Höhe wie die InP-NW-Arrays ist in Abb. 4 gezeigt. Im Allgemeinen steigt die Lichtsammelfähigkeit anfangs an, erreicht ihren maximalen Wert und fällt allmählich ab, wenn sich der FR einem größeren Wert nähert. Dieser Trend wird der Änderung des durchgelassenen und reflektierten Lichts zugeschrieben, wenn sich die komplexen Brechungsindizes aufgrund von FR-Variationen ändern. Insbesondere wenn FR von 0,05 auf 0,2 ansteigt, wird aufgrund der Zugabe von InP-Material mehr Licht absorbiert, bevor es aus den NW-Anordnungen durchgelassen wird. Dieser Trendanstieg jedoch, bis FR 0,2 erreicht, und ein weiterer Anstieg von FR verursacht einen hohen komplexen Brechungsindex der äquivalenten Schicht, was zu einer optischen Impedanz zwischen den Luft- und NW-Arrays führt. Als Ergebnis steigt das Reflexionsvermögen an der einfallenden Oberfläche schnell an, was die Lichtabsorption verringert [13]. Daher beträgt der optimale Wert für FR 0,2 und die Periodizitäten für quadratisch und hexagonal angeordnete NW-Arrays betragen 364,63 bzw. 391,82 nm.

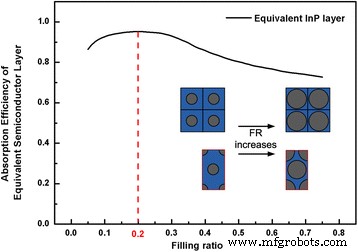
Absorptionseffizienz der effektiven Mediumschicht für InP-NW-Arrays als Funktion von FR

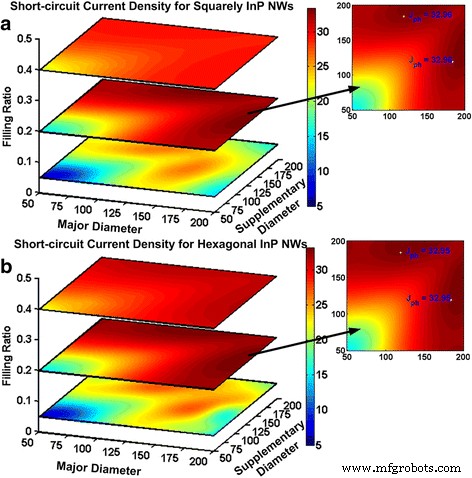
Die Kurzschlussstromdichten für verschiedene Kombinationen von Durchmessern und FRs sind in Abb. 5 dargestellt. Es zeigt deutlich, dass die Anordnung der NWs wenig Einfluss auf die höchste Lichtabsorption hat. Unabhängig von den Anordnungen von NW-Arrays kann unser Verfahren sowohl angewendet werden als auch genaue Ergebnisse erzielen. Das maximale J _sc mit berechneten optimalen geometrischen Abmessungen für InP NW-Arrays werden für quadratische bzw. hexagonale Anordnung berechnet. Das analytisch vorhergesagte maximale J _sc beträgt 32,11 und 32,06 mA/cm ² für quadratische und hexagonale NW-Arrays, was zu einer Toleranz von 0,33 bzw. 0,1 % im Vergleich zu den FDTD-Simulationsergebnissen führt.

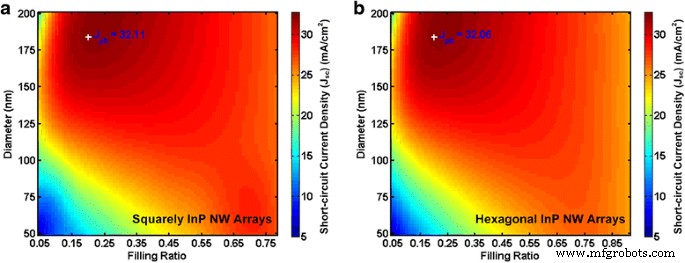
Theoretisch vorhergesagte Maximalwerte im Vergleich zu FDTD-Simulationen. a Quadratisch und b hexagonale InP NW Arrays mit einfachem Durchmesser

B. Maximales Lichtsammeln für InP-NWs mit doppeltem Durchmesser

Das Hinzufügen eines sekundären Durchmessers zu den NW-Arrays wurde von mehreren Gruppen untersucht, um die Sonnenenergieernte durch zeitaufwändige Simulationen weiter zu erhöhen [22, 29] [34]. Aus der obigen Diskussion bietet unsere Methode eine Möglichkeit, sich schnell den erforderlichen NW-Durchmessern anzunähern. Die Resonanzwellenlänge der zusätzlichen NWs sollte dem Absorptionstal des Hauptdurchmessers der NWs entsprechen, das 585 nm beträgt, wie in Abb. 3b gezeigt. Außerdem sollten die NWs nur einen Resonanzmodus unterstützen. Diese beiden Schlussfolgerungen führen zu D _zusätzlich von 119 nm. Die optimale FR von 0,2 gilt immer noch in den InP-NW-Arrays mit doppeltem Durchmesser, und die Periodizität wird mit 307 und 329,95 nm für eine quadratische und hexagonale Anordnung von NW-Arrays berechnet. Abbildung 6 gibt einen Überblick über die Variation der Kurzschlussstromdichte als Funktion von D _Hauptfach , D _zusätzlich , und FR für zwei Arten von NW-Arrays. Im Allgemeinen nimmt die Lichtausbeute mit FR zu, erreicht ihren Maximalwert und fällt ab. Wenn FR 0,2 beträgt, zeigen die Einschübe in Abb. 6 das höchste J . an _sc von 32,96 und 32,95 mA/cm ² sowohl für quadratische als auch für hexagonale InP-NWs. Verglichen mit den Maximalwerten aus Simulationen von 33,34 und 33,26 mA/cm ² , die Toleranzen betragen 1,1 und 0,9% für quadratische und sechseckige NWs. Abbildung 6 zeigt auch, dass mit zunehmendem FR die Kopplung zwischen benachbarten NWs nicht übersehen werden kann. Leistung kann zu den benachbarten NWs übertragen werden, die denselben Leckmodus unterstützen, was zu einer Konkurrenz der einfallenden Energie [35] führt, die sich nachteilig auf die Gesamtlichtabsorption auswirkt. Wenn der FR für beide Anordnungen gleich ist, p_Quadrat ² /p_hexagonal ² ist \(\sqrt{3}/2\). Daher ist das p _sechseckig ist das 1,08-fache des p _Quadrat die weniger Modenkopplung zwischen NWs hat als quadratische Arrays. Dies erklärt die Unterschiede des Lichtsammelns der beiden Arrays, wenn FR 0,05 und 0,4 beträgt.

Kurzschlussstromdichten als Funktion von großen, zusätzlichen Durchmessern und FRs. a Quadratisch und b hexagonale InP-NW-Arrays, bei denen die Einsätze optimale Durchmesser für die jeweiligen NW-Anordnungen aufweisen

C. Maximales Lichtsammeln für InP-NWs mit vier Durchmessern

Mehrere Durchmesser von NW-Arrays ziehen auch viel Forschungsinteresse auf sich, um eine Absorption von nahezu eins über die absorbierende Region zu erreichen [29]. Es wird jedoch nur eine begrenzte Anzahl von Durchmesserkombinationen bereitgestellt, da die Massendatenerfassung viel Zeit erfordert. Dieses Problem kann in unserer analytischen Designmethode gelöst werden, und als Beispiel werden vier Durchmesser von quadratisch angeordneten InP-NW-Arrays angegeben. Die Gesamtzeit, die benötigt wird, um alle Berechnungen mit unserer Methode abzuschließen, entspricht der Zeit, die nur eine FDTD-Simulation mit demselben PC benötigt. Bei der Erfassung des Haupt- und Ergänzungsdurchmessers von NWs können der dritte und vierte Durchmesser von NWs auf ähnliche Weise berechnet werden. Die Überlagerung der normalisierten Absorptionseffizienz des Haupt- und Zusatzdurchmessers von NWs ist in Abb. 7 dargestellt, wobei die Absorptionstäler bei 486 und 704 nm liegen. Daher können der dritte und vierte Durchmesser von NWs berechnet werden, um die Bedingungen zu erfüllen, dass jeder von ihnen nur eine Mode unterstützt, und die Resonanzwellenlängen stimmen mit den beiden Absorptionstälern in 7 überein. Dementsprechend sind der dritte und vierte Durchmesser für InP-NW-Arrays werden als 92 und 148 nm erhalten. Mit der optimalen FR von 0,2, deren Gültigkeit unabhängig von der Anordnung von NW und Durchmessern ist, kann die Periodizität für InP-NW-Arrays zu 277,41 nm erhalten werden.

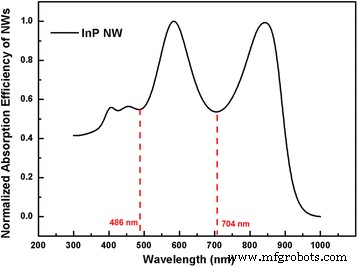
Superposition of the absorption efficiencies of the major and the supplementary diameters of InP NWs

The light absorption spectrum for the optimal combination of four NWs is provided in Fig. 8 from which the near-unity light absorption is achieved by the well selection of individual NWs. FDTD simulation results with four diameters’ combinations for squarely arranged NW arrays are shown in Fig. 9. To gain an overview of this multi-parameter optimization problem, two sets of coordinates are employed. The inner x und y axes denote the major and supplementary diameters whereas the outer x und y axes represent the third and fourth diameters. Due to the huge number of combinations of diameters, limited third and fourth diameters are deliberately selected to represent the whole absorption trend. From Fig. 3, the 80 nm is chosen as single mode resonance within NWs; 140 nm reflects the evolvement from single to double modes existence in NWs; 170 nm indicates the upper end of double modes existence while remain FWHM lying within absorbing region. Each intersect of the dash lines indicates different combination of the third and fourth diameters whereas the major and supplementary diameter run through 50 to 200 nm. When the diameters have larger values than 140 nm in Fig. 9, the majority of combinations of diameters will lead to the J _sc above 30 mA/cm ² . When all of the diameters reach above 170 nm, the average of J _sc can be 32 mA/cm ² . These results are also reflected in Figs. 5a and 6a. Compared with single or double diameter NW arrays, optimized four diameter NW arrays indeed lead to higher J _sc . The highest J _sc for four diameters InP NW arrays with our calculated geometrical dimensions is 33.13 mA/cm ² with a tolerance of 2.2%.

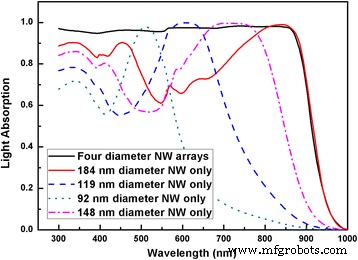
Light absorption of four diameter InP NW arrays

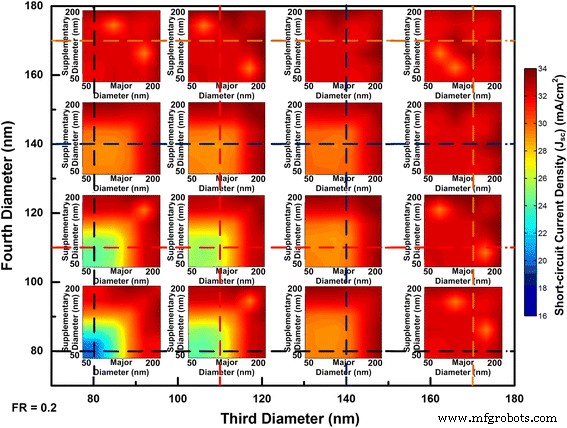
Short-circuit current densities change with the major, supplementary, third, and fourth InP NWs

Schlussfolgerungen

In this study, we present model for effective and fast design of both squarely and hexagonal InP NW arrays to achieve the highest light harvesting for photovoltaic application. Geometrical dimensions for vertically aligned single, double, and multiple diameters of NW arrays are investigated. Compared with time-consuming FDTD simulations, our predicted maximal short-circuit current densities with calculated three-dimensional NW arrays remain tolerances below 2.2% for all cases. For single diameter NW arrays, the optimal diameter is 184 nm which is only 4 nm difference to the reported highest efficiency InP NW solar cells. In the multiple diameter NW arrays, the diameters of the rest of NWs are optimized to satisfy the conditions that they support only one resonant mode and the corresponding wavelengths match the absorption valley of the major NWs. Moreover, the FR of the NW array is optimized to be 0.2 by creating an effective medium layer which is regardless of the diameter, periodicity, and arrangements of NWs. Compared with the optical modeling, the predicted highest short-circuit current densities for single diameter NW arrays lie within 0.33 and 0.1% tolerance for squarely and hexagonal NW array. The arrangements of NW array have little influence on the light absorption with optimal geometrical parameters, but the coupling among neighboring NWs becomes serious for multiple diameter NWs at large FR value. Squarely arranged four diameter NW arrays were also presented and the highest short-circuit current densities predicted to be 33.13 mA/cm ² with a low tolerance of 2.2%. The time-efficient, high precision with wide suitability of the proposed design for InP NW arrays demonstrate itself to be a promising tool to guide practical NW-based solar cell design.

Abkürzungen

FDTD:

Finite-difference time-domain

FR:

Filling ratio

FWHM:

Volle Breite auf halbem Maximum

NPs:

Nanoparticles

NWs:

Nanowires