Gleichzeitige Erzeugung mehrerer dreidimensionaler Traktorkurvenstrahlen

Einführung

Schon vor langer Zeit haben Menschen bewiesen, dass Licht Kräfte ausüben kann. Auch die Idee, Objekte mit optischen Strahlen anzulocken, hat unsere Aufmerksamkeit schon lange auf sich gezogen. Aufgrund der Phasensingularität und des einzigartigen Bahndrehimpulses hat der optische Wirbel einen wichtigen Forschungswert in den Bereichen optische Mikromanipulation, Quantenkommunikation, optische Bildgebung und optische Messung [1,2,3,4,5,6]. Obwohl die Technologie zum Erzeugen optischer Wirbel entwickelt wurde und in verschiedenen Anwendungen wertvoll sein kann, ist die Effizienz eines einzelnen optischen Wirbels immer noch gering. Um mehrere Partikel gleichzeitig einzufangen und verschiedene Partikel separat zu betreiben, ist die Erzeugung optischer Wirbelarrays zu einem heißen Thema geworden [7, 8].

Neuere theoretische Studien [9,10,11,12,13] haben gezeigt, dass ein Traktorstrahl eine Wanderwelle ist, die beleuchtetes Material entlang seiner Länge zurück zu seiner Quelle transportieren kann. Neue Fortschritte in der Laserstrahlsteuerung haben zur experimentellen Realisierung von Traktorstrahlen geführt [14, 15]. Ein wichtiger Typ von 3D-Wirbelfallen ist der sogenannte Solenoid-Beam, der eine feste Spiralform um die optische Achse aufweist [16], bei dem der Phasengradient entlang dieser Kurve vorgegeben werden kann, um einen Traktorstrahl zu erhalten. Dies wurde erreicht, indem einer kollinearen Überlagerung von Bessel-Strahlen helikale Phasen überlagert wurden. Ruffner und Grier [17] demonstrierten und analysierten experimentell die Eigenschaften einer Klasse von Traktorstrahlen, die durch die Interferenz zweier koaxialer Besselstrahlen erhalten wurden, die sich in ihren axialen Wellenzahlen unterscheiden. 2013 haben Rodrigo et al. präsentieren ein Verfahren zur effizienten Erzeugung von Traktorstrahlen durch Laden entworfener Nur-Phasen-Hologramme in den Spatial Light Modulator (SLM) und währenddessen Bestrahlen des SLM mit Lasern. Sie nutzten die Technik, um die Erzeugung von hochintensiven Gradientenstrahlen (HIG) zu ermöglichen, deren Phase und Intensität basierend auf dem computergenerierten Hologramm (CGH) vorgegeben werden [18]. Sie haben experimentell bewiesen, dass die Strahlen in unterschiedlichen 3D-Geometrien geformt werden können. Die HIGs und Phasengradientenkräfte sind entscheidend für den Bau von 3D-Laserfallen, die auch gegen Lichtstrahlungsdruck mehrere Partikel bewegen können [19]. Rodrigo zeigte auch, dass eine Freistil-Laserfalle, einschließlich HIG- und Phasengradientenkräften, mehrere Partikel einschließen und ihre Bewegung antreiben konnte [20]. Die meisten der berichteten Arbeiten konzentrieren sich jedoch auf die Erzeugung einfacher 3D-Traktorstrahlen, was bei der Weiterentwicklung von Anwendungen der Strahlformung Grenzen hat. Basierend auf der obigen Analyse wird dringend eine fortschrittliche Strahlformungstechnologie zur Erzeugung mehrerer 3D-Traktorstrahlen benötigt.

In diesem Papier demonstrieren wir die Methode zur Erzeugung mehrerer 3D-Traktorstrahlen unter Verwendung der modifizierten holographischen Strahlformungstechnik, bei der alle CGHs gemultiplext und durch Hinzufügen des jeweiligen linearen Phasengitters zu einem Nur-Phasen-Hologramm codiert werden. Wir entwerfen mehrere 3D-Traktorträger, die in verschiedenen Winkeln verdreht sind. Von solchen>neuen Traktorstrahlen wird erwartet, dass sie das Anwendungsgebiet optischer Wirbel erweitern und potenziell nützlich bei der Realisierung hochleistungsfähiger mehrfacher optischer Anwendungen sind.

Methoden

Abbildung 1a zeigt das Schema einer holographischen 3D-Strahlformungstechnik in [18], die es ermöglicht, komplexe Strahlen zu entwerfen, deren Intensitäts- und Phasenverteilung einer vorgegebenen 3D-Kurve folgt. Die Codierung des komplexen Amplitudenfeldes in holographische Phasengitter ist ein Verfahren zur Berechnung von CGH. Um einen gewünschten Fokusstrahl zu erzeugen, ist die komplexe Amplitude der Einfallsebene insbesondere durch den Ausdruck gegeben:

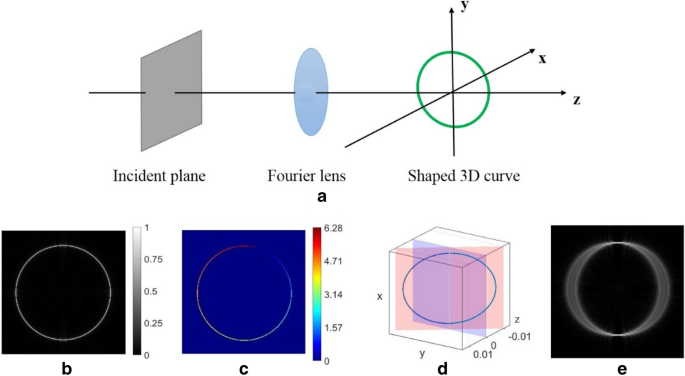
a Schema der holographischen 3D-Strahlformungstechnik. b , c Rekonstruierte Intensitäts- und Phasenverteilung der 2D-Ringkurve in der Fokusebene. d Räumliches Schema einer relativ zur Ebene z geneigten Ringkurve = 0. e Der auf die Brennebene fokussierte Ringtraktorstrahl (z = 0)

Die Begriffe ψ (x , y , t ) und φ (x , y , t ) in Gl. (1) werden bestimmt durch

[x ₀ (t ), y ₀ (t ), z ₀ (t )] stellt die vorgeschriebene 3D-Kurve in der kartesischen Koordinate mit t . dar ∈[0,2π ]. f ₀ und λ beziehen sich auf die Brennweite der Fourier-Linse bzw. die Wellenlänge.

Gl. (1) ermöglicht die Berechnung des einfallenden komplexen Feldes (nämlich komplexes CGH), das einen strukturell stabilen Fokusstrahl mit spezieller Intensitätsverteilung und Phasengradient (helikale Phase entlang der Kurve) formen kann. Wir betrachten zunächst eine 2D-Ringkurve x ₀ (t ) = Rcos(t ), y ₀ (t ) = Rsin(t ). Die Intensitätsverteilung des resultierenden Strahls ist in Abb. 1b dargestellt. Die Phasenverteilung des Rings ist entlang von Kurven unter der topologischen Ladung von m = 1 gut definiert [siehe Abb. 1c]. Wir betrachten einen gekippten Ring in Abb. 1d. Die Ebene der Ringkurve, die ausgehend von der Ebene z . um einen bestimmten Winkel geneigt ist =0. In diesem Fall wird der Strahl fokussiert und erscheint an den oberen und unteren Punkten [siehe Fig. 1e].

Um verschiedene im Fokusfeld teilweise getrennte Traktorkurvenstrahlen zu multiplexen, wird jedes komplexe CGH, berechnet nach Gl. (1) muss mit einer eindeutigen Trägerfrequenz codiert werden. Dies kann durch Hinzufügen eines linearen Phasengitters zum Hologramm jedes Strahls erreicht werden. Lineare Gitter in Kombination mit Raumfiltern werden üblicherweise verwendet, um die erste Beugungsordnung von unerwünschten nullten und höheren Beugungsordnungen zu isolieren. Die Übertragungsfunktion eines linearen Phasengitters ist gegeben als

du _ich und v _ich sind die Raumkoordinaten des erzeugten Strahls im Fernfeld, erreicht mit einer Fourier-Linse der Brennweite f ₀ . k = 2π /λ ist die Wellenzahl und z _ich ist die axial verschobene Verschiebung weg von der Fokusebene (Fourier-Ebene). Um gleichzeitig Traktorkurvenstrahlen zu erzeugen, müssen die Ausdrücke des endgültigen komplexen CGH durch

Ergebnisse und Diskussion

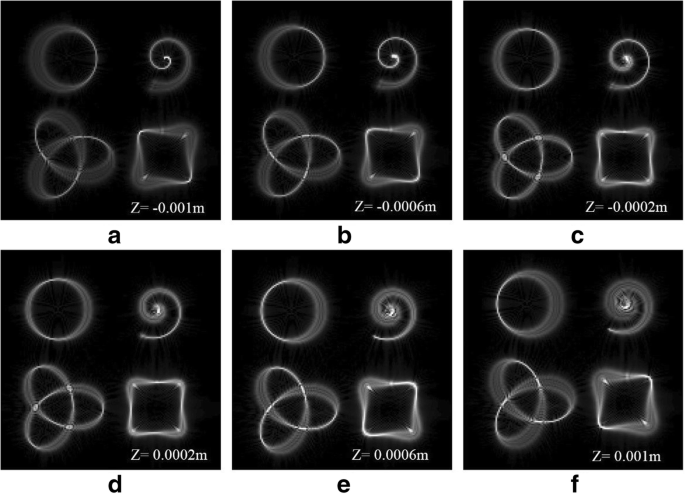
Die Lichtfeldregulierung bei 3D-Konfiguration ist in praktischen Anwendungen, wie der 3D-Manipulation von Partikeln in einer fluiden Umgebung, sehr sinnvoll. Daher untersuchen wir die Erzeugung von HIG-Strahlen, deren Intensität und Phase entlang von 3D-Kurven unterschiedlicher Form vorgegeben werden. Konkret betrachten wir einen geneigten Ring Abb. 2a–e, eine archimedische Spirale Abb. 2f–j, eine kleeblattgeknüpfte Kurve Abb. 2k–o und eine quadratische Kurve Abb. 2p–t. Die entsprechenden Kurvenausdrücke sind in Tabelle 1 angegeben. Diese 3D-Strukturen werden entlang der Strahlausbreitung im Fokusbereich sichtbar. Die in der Fokusebene gemessenen Strahlintensitätsverteilungen (z = 0) sind in der dritten Spalte von Abb. 2 dargestellt. Die Z Koordinaten, die anderen Spalten von Fig. 2 entsprechen, sind in den Simulationsdiagrammen markiert.

Simulationsergebnisse von 3D-Traktorstrahlen. ein –e Ringkurve von 3D-Traktorstrahlen fokussiert auf verschiedene z Flugzeuge. f –j Archimedische Spirale aus 3D-Traktorstrahlen, die auf verschiedene z . fokussiert sind Flugzeuge. k –o Kleeblatt-verknotete Kurve von 3D-Traktorstrahlen, die auf verschiedene z . fokussiert sind Flugzeuge. p –t Quadratische Kurve von 3D-Traktorstrahlen fokussiert auf verschiedene z Flugzeuge

Im Bereich der optischen Mikromanipulation können Traktorstrahlen mit unterschiedlichen 3D-Verzerrungen eine größere Rolle bei Anwendungen spielen. Für eine höhere Effizienz ist es jedoch in hohem Maße erwünscht, differenzierte Manipulationen an verschiedenen Orten synchron auszuführen. Daher entwerfen wir gleichzeitig mehrere Traktorstrahlen mit vier Mustern, von denen jedes verwendet werden kann, um gegebene Partikel in jeder vorgeschriebenen geometrischen Kurve mit einem gewissen Grad an 3D-Verzerrung einzuschließen. Die relative Position der Schlepperbalken kann gestaltet werden. Um zu zeigen, dass mehrere Traktorstrahlen auf die 3D-Region fokussiert sind, haben wir sechs zu beobachtende 2D-Ebenen ausgewählt. Die Traktorstrahlen werden auf verschiedene 2D-Ebenen fokussiert, siehe Abb. 3. Diese 3D-Strukturen werden entlang der Strahlausbreitung im Fokusbereich sichtbar.

Simulationsergebnisse mehrerer 3D-Traktorstrahlen an verschiedenen Standorten. a –c Rekonstruierte Intensität der Strahlen vor der Fokusebene. d –f Rekonstruierte Intensität der Strahlen nach der Fokusebene

Um die Interaktion mehrerer manipulierter Partikel zu beobachten, haben wir kupferähnliche verschachtelte grafische Traktorstrahlen entworfen. Die 3D-Verzerrung und die Formen der inneren und äußeren Balken können separat entworfen werden. Die Ringkurve ist auf die Ebene fokussiert (z = 0), und die quadratische Kurve weist einen gewissen Grad an 3D-Verzerrung auf [siehe Abb. 4a–e]. Die quadratische Kurve ist auf die Ebene fokussiert (z = 0), und die Ringkurve weist einen gewissen Grad an 3D-Verzerrung auf [siehe Abb. 4f–j]. Die in der Fokusebene gemessenen Strahlintensitätsverteilungen (z = 0) sind in der dritten Spalte von Abb. 4 dargestellt. Die z Koordinaten, die anderen Spalten von Fig. 4 entsprechen, sind in den Simulationsdiagrammen markiert. Die Form der Traktorstrahlen kann flexibel angepasst werden, um die Partikel an verschiedenen Positionen zu kontrollieren.

Simulationsergebnisse von kupferartig verschachtelten grafischen Traktorstrahlen. a –e Strahlen, die in einer geneigten quadratischen Kurve geformt sind, werden auf verschiedene z . fokussiert Flugzeuge. f –j Strahlen, die in einer geneigten Ringkurve geformt sind, werden auf verschiedene z . fokussiert Flugzeuge

Optische Experimente wurden durchgeführt, um zu verifizieren, dass das oben eingeführte Verfahren verwendet werden kann, um den Zweck der Fokussierung mehrerer 3D-Traktorstrahlen in abstimmbaren Fokussierungsbereichen zu erreichen. Wie in Fig. 5 gezeigt, besteht der optische Aufbau zum Erzeugen des 3D-Traktorstrahls aus einem Flüssigkristall-Raumlichtmodulator (SLM), einem 4f-Filtersystem und einer Fourier-Transformations-(Fokussierungs-)Linse. Ein Festkörperlaser mit einer Wellenlänge von 532 nm wird zur ebenen Wellenbeleuchtung kollimiert. Der SLM (Holoeye Pluto, 8 Pixel Pitch, 1920 × 1080 Auflösung) wird verwendet, um ein Nur-Phasen-CGH zu adressieren. Wir verwenden die Doppelphasenmethode [18, 20], um das komplexe CGH H . zu kodieren (x ,y ) berechnet nach Gl. (4) in ein Nur-Phasen-CGH. Sie besteht darin, die komplexe Funktion als Hologramm in den SLM zu kodieren. Der durch SLM modulierte Strahl wird dann auf die hintere Apertur der Fourier-Transformationslinse projiziert (f = 400 mm) durch eine optische 4f-Filterkonfiguration. In der Fourier-Ebene der Fokussierlinse wird eine ladungsgekoppelte (CCD) Kamera platziert, um die erzeugten Intensitätsmuster aufzuzeichnen. Die Ergebnisse der 3D-Traktorstrahlen sind in Abb. 6 dargestellt. Obwohl die resultierenden Strahlen nach dem Durchgang durch das optische 4f-System Fehler aufweisen, stimmen sie gut mit den Simulationsergebnissen überein.

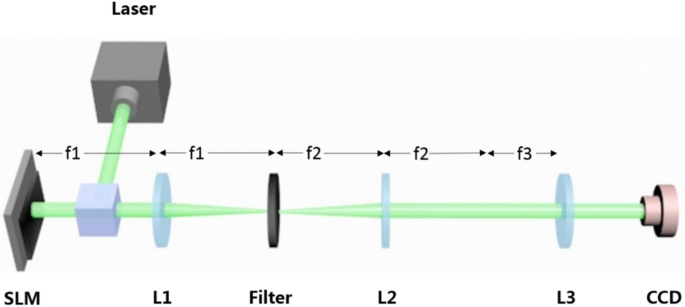
Versuchsaufbau. Das Hologramm wird in den SLM adressiert, der von einem kollimierten Laserstrahl beleuchtet wird. Nachdem der Strahl die Linse 1 passiert hat, kann das gewünschte Muster mit einer Blende gefiltert werden. Die resultierenden Strahlen passieren dann Objektiv 2 und Objektiv 3 und können von der Kamera erfasst werden

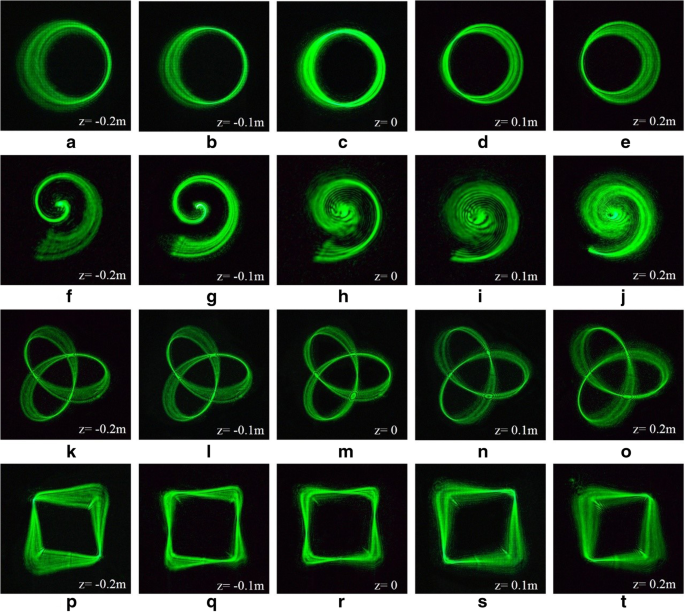
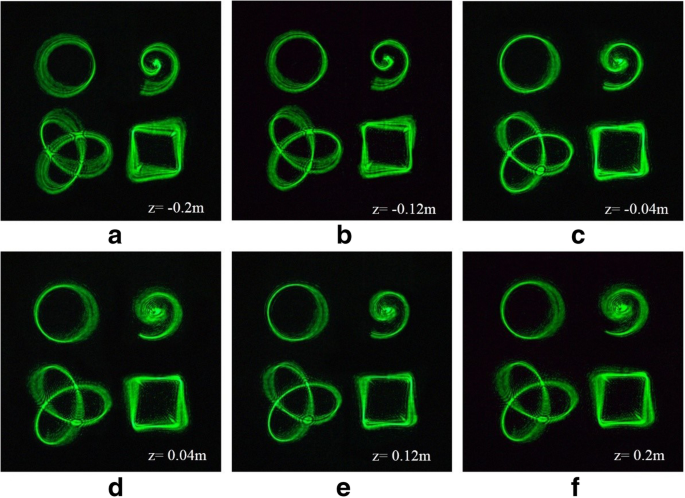
Experimentelle Ergebnisse von 3D-Traktorträgern. a –e Ringkurve von 3D-Traktorstrahlen fokussiert auf verschiedene z Flugzeuge. f –j Archimedische Spirale aus 3D-Traktorstrahlen, die auf verschiedene z . fokussiert sind Flugzeuge. k –o Kleeblatt-verknotete Kurve von 3D-Traktorstrahlen, die auf verschiedene z . fokussiert sind Flugzeuge. p –t Quadratische Kurve von 3D-Traktorstrahlen fokussiert auf verschiedene z Flugzeuge

Die Ergebnisse der mehreren 3D-Traktorstrahlen sind in Abb. 7 dargestellt. Wir haben sechs 2D-Ebenen zur Beobachtung ausgewählt, was für den Vergleich mit der Simulation geeignet ist. Die Simulationsergebnisse stimmen gut mit den experimentellen Ergebnissen überein. Es ist nachgewiesen, dass mit dieser Methode mehrere 3D-Traktorstrahlen flexibel und effizient erzeugt werden können. Verschiedene Strahlen mit einem gewissen Grad an 3D-Verzerrung können Partikel einschließen.

Experimentelle Ergebnisse mehrerer 3D-Traktorstrahlen an verschiedenen Orten. a –c Rekonstruierte Intensität der Strahlen vor der Fokusebene. d –f Rekonstruierte Intensität der Strahlen nach der Fokusebene

Die Ergebnisse kupferartig verschachtelter grafischer Traktorstrahlen sind in Abb. 8 dargestellt. Die Simulationsergebnisse stimmen gut mit den experimentellen Ergebnissen überein. Somit interagieren die beiden verschachtelten Strahlen kaum miteinander. Die Traktorstrahlen können für die Multi-Partikel-Manipulation in verschiedenen Kurven verwendet werden.

Experimentelle Ergebnisse kupferartig verschachtelter grafischer Traktorbalken. a –e Strahlen, die in einer geneigten quadratischen Kurve geformt sind, werden auf verschiedene z . fokussiert Flugzeuge. f –j Strahlen, die in einer geneigten Ringkurve geformt sind, werden auf verschiedene z . fokussiert Flugzeuge

Schlussfolgerung

Wir konstruieren mehrere 3D-Traktorträger, deren räumliche Lage unabhängig voneinander geregelt wird. Inzwischen könnte jeder einzelne Strahl entlang beliebiger geometrischer Kurven vorgeschrieben und nach Wunsch in beliebigen Winkeln verdreht werden. Wir beweisen theoretisch und experimentell, dass die Erzeugung optischer Traktorstrahlen in 3D-Konfiguration ohne weiteres erreicht werden kann. Hochintensive Gradienten und Phasengradienten haben die Fähigkeit, Partikel einzufangen. Derzeit werden Experimente durchgeführt und die optischen Wirbelstrahlen schädigen die Partikel minimal. Unsere Arbeit erweitert die Arten von Traktorträgern. Es wird als sinnvoll und nützlich für die Weiterentwicklung von Traktorstrahlen für mehrere optische Anwendungen angesehen.

Abkürzungen

2D:

Zweidimensional

3D:

Dreidimensional

CGH:

Computergeneriertes Hologramm

HIG:

Hoher Intensitätsgradient

SLM:

Räumlicher Lichtmodulator