Digitale Logikfunktionen

Wir können eine einfache Logikfunktion für unseren hypothetischen Lampenkreis aufbauen, indem wir mehrere Kontakte verwenden, und diese Schaltungen ganz einfach und verständlich mit zusätzlichen Sprossen zu unserer ursprünglichen „Leiter“ dokumentieren.

Wenn wir die standardmäßige binäre Notation für den Status der Schalter und der Lampe verwenden (0 für unbetätigt oder nicht erregt; 1 für betätigt oder erregt), kann eine Wahrheitstabelle erstellt werden, um zu zeigen, wie die Logik funktioniert:

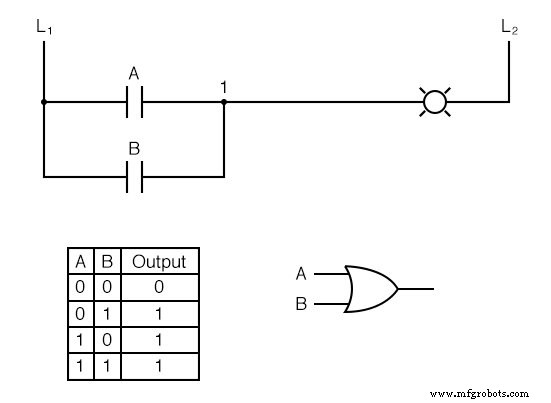
Jetzt geht die Lampe an, wenn entweder Kontakt A oder Kontakt B betätigt wird, da die Lampe nur über mindestens einen Strompfad von der Ader L₁ mit Strom versorgt wird zu Draht 1.

Was wir haben, ist eine einfache ODER-Logikfunktion, die nur mit Kontakten und einer Lampe implementiert wird.

Wir können die UND-Logikfunktion nachahmen, indem wir die beiden Kontakte in Reihe statt parallel verdrahten:

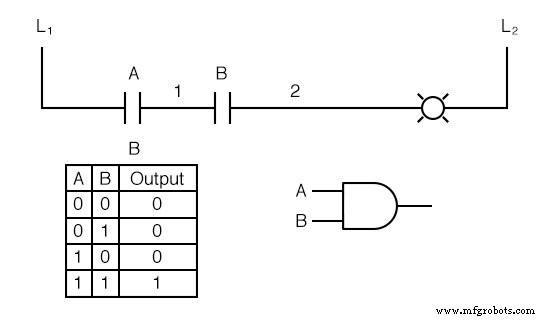
Jetzt wird die Lampe nur erregt, wenn Kontakt A und Kontakt B werden gleichzeitig betätigt.

Es existiert ein Pfad für Strom von Ader L₁ zur Lampe (Draht 2), wenn und nur wenn beide Schaltkontakte sind geschlossen.

Die logische Umkehr- oder NICHT-Funktion kann an einem Kontakteingang ausgeführt werden, indem einfach ein Öffner anstelle eines Schließers verwendet wird:

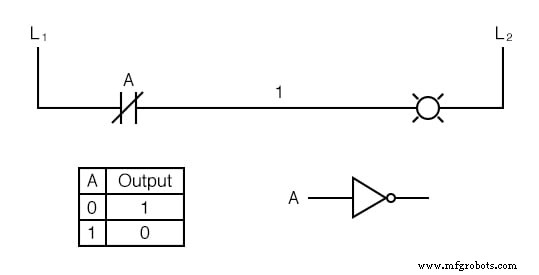
Jetzt wird die Lampe erregt, wenn der Kontakt nicht ist betätigt und fällt ab, wenn der Kontakt betätigt wird.

Wenn wir unsere ODER-Funktion nehmen und jeden „Eingang“ durch die Verwendung von Öffnerkontakten invertieren, erhalten wir am Ende eine NAND-Funktion.

In einem speziellen Zweig der Mathematik, der als Boolesche Algebra bekannt ist , dieser Effekt der Änderung der Gatterfunktionsidentität mit der Inversion von Eingangssignalen wird durch DeMorgans Theorem . beschrieben , ein Thema, das in einem späteren Kapitel genauer untersucht wird.

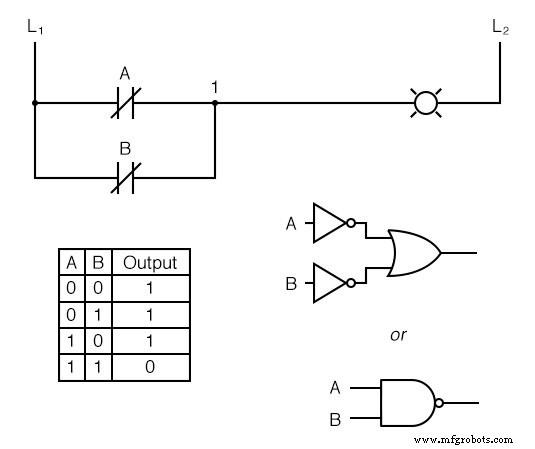
Die Lampe wird eingeschaltet, wenn entweder Kontakt ist unbetätigt. Es erlischt nur, wenn beide Kontakte werden gleichzeitig betätigt.

Wenn wir unsere UND-Funktion nehmen und jeden „Eingang“ durch die Verwendung von Öffnerkontakten invertieren, erhalten wir eine NOR-Funktion:

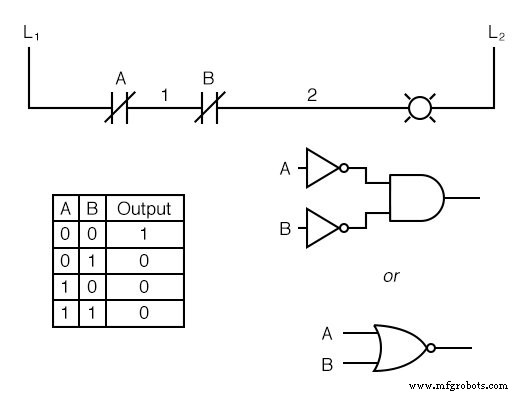
Ein Muster offenbart sich schnell, wenn Ladder-Schaltungen mit ihren Gegenstücken mit logischen Gattern verglichen werden:

• Parallelkontakte entsprechen einem ODER-Gatter.
• Serienkontakte entsprechen einem UND-Gatter.
• Normal geschlossene Kontakte entsprechen einem NICHT-Gatter (Wechselrichter).

Wir können auch kombinatorische Logikfunktionen erstellen, indem wir Kontakte in Reihen-Parallel-Anordnungen gruppieren. Im folgenden Beispiel haben wir eine Exklusiv-ODER-Funktion, die aus einer Kombination von UND-, ODER- und Inverter-(NICHT-)Gattern aufgebaut ist:

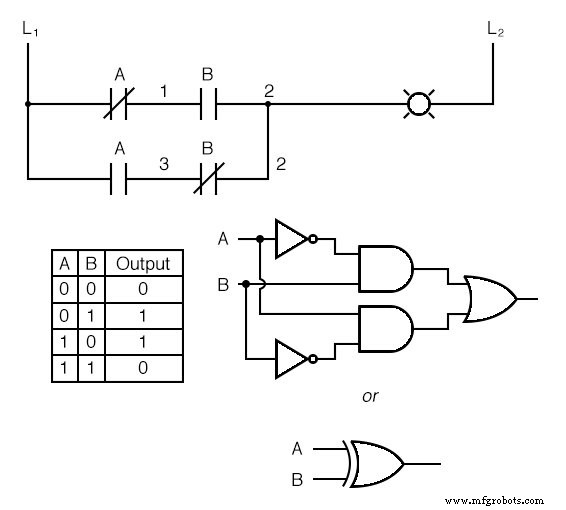
Die oberste Sprosse (Öffner A in Reihe mit Schließer B) entspricht der oberen NICHT/UND-Gatterkombination.

Die unterste Sprosse (Schließer A in Reihe mit Öffner B) entspricht der unteren NOT/AND-Gatterkombination.

Die parallele Verbindung zwischen den beiden Sprossen an Draht Nummer 2 bildet das Äquivalent des ODER-Gatters, indem es entweder Sprossen 1 oder Sprossen 2 ermöglicht, die Lampe zu erregen.

Entwerfen einer Exklusiv-ODER-Funktion

Um die Exklusiv-ODER-Funktion zu realisieren, mussten wir zwei Kontakte pro Eingang verwenden:einen für den direkten Eingang und den anderen für den „invertierten“ Eingang.

Die beiden „A“-Kontakte werden physisch durch denselben Mechanismus betätigt, ebenso wie die beiden „B“-Kontakte.

Die gemeinsame Assoziation zwischen Kontakten wird durch das Label des Kontakts gekennzeichnet.

Es gibt keine Begrenzung, wie viele Kontakte pro Schalter in einem Kontaktplan dargestellt werden können, da jeder neue Kontakt an jedem im Diagramm verwendeten Schalter oder Relais (entweder Schließer oder Öffner) einfach mit dem gleichen Label gekennzeichnet wird.

Manchmal werden mehrere Kontakte an einem einzelnen Schalter (oder Relais) mit zusammengesetzten Etiketten wie „A-1“ und „A-2“ anstelle von zwei „A“-Etiketten gekennzeichnet.

Dies kann besonders nützlich sein, wenn Sie speziell festlegen möchten, welcher Kontaktsatz an jedem Schalter oder Relais für welchen Teil eines Stromkreises verwendet wird.

Der Einfachheit halber verzichte ich in dieser Lektion auf solch aufwendige Beschriftungen. Wenn Sie ein gemeinsames Label für mehrere Kontakte sehen, wissen Sie, dass diese Kontakte alle durch denselben Mechanismus aktiviert werden.

Wenn wir die Ausgabe invertieren möchten jeder schaltererzeugten Logikfunktion müssen wir ein Relais mit einem Öffnerkontakt verwenden.

Wenn wir beispielsweise eine Last basierend auf der Umkehrung oder NICHT eines Schließerkontakts erregen möchten, könnten wir Folgendes tun:

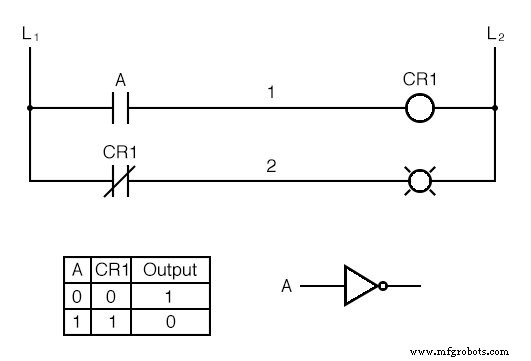
Wir nennen das Relais „Steuerrelais 1“ oder CR₁ . Wenn die Spule von CR₁ (symbolisiert durch das Klammerpaar auf der ersten Sprosse) wird erregt, der Kontakt auf der zweiten Sprosse öffnet , wodurch die Lampe abgeschaltet wird.

Von Schalter A zur Spule von CR₁ , ist die Logikfunktion nicht invertiert. Der von der Relaisspule CR₁ betätigte Öffnerkontakt bietet eine logische Wechselrichterfunktion, um die Lampe entgegen dem Betätigungsstatus des Schalters anzusteuern.

Wenn wir diese Inversionsstrategie auf eine unserer zuvor erstellten Funktionen mit invertiertem Eingang anwenden, z. B. OR-to-NAND, können wir den Ausgang mit einem Relais invertieren, um eine nicht invertierte Funktion zu erstellen:

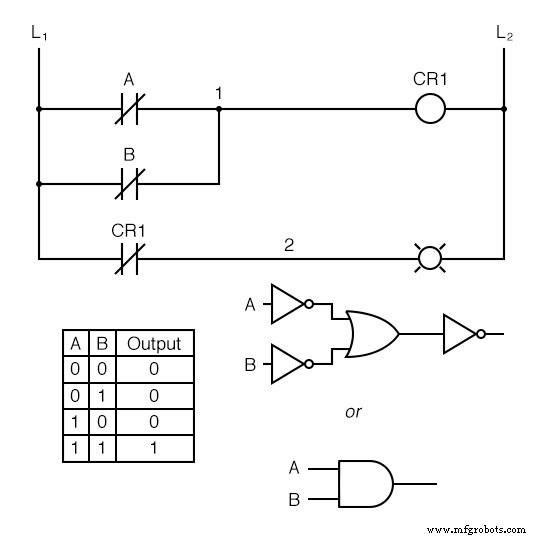
Von den Schaltern zur Spule von CR₁ , die logische Funktion ist die eines NAND-Gatters. CR₁ Der normalerweise geschlossene Kontakt des Benutzers bietet eine letzte Umkehrung, um die NAND-Funktion in eine UND-Funktion umzuwandeln.

REZENSION :

• Parallelkontakte entsprechen logisch einem ODER-Gatter.
• Serienkontakte entsprechen logisch einem UND-Gatter.
• Normal geschlossene (N.C.) Kontakte sind logisch äquivalent zu einem NICHT-Tor.
• Ein Relais muss verwendet werden, um den Ausgang zu invertieren einer logischen Gatterfunktion, während einfache Öffnerkontakte ausreichen, um invertierte Gatter Eingänge represent darzustellen .

VERWANDTE ARBEITSBLÄTTER:

• Arbeitsblatt zur Booleschen Algebra
• Arbeitsblatt zur elektromechanischen Relaislogik
• Arbeitsblatt für digitale Logiksignale