Superpositionssatz

Der Superpositionssatz ist einer dieser Geniestreiche, der ein komplexes Thema auf eine sinnvolle Weise vereinfacht. Ein Satz wie der von Millman funktioniert sicherlich gut, aber es ist nicht ganz klar warum es funktioniert so gut. Überlagerung hingegen ist offensichtlich.

Serien-/Parallelanalyse

Die im Superpositionssatz verwendete Strategie besteht darin, alle bis auf eine Stromquelle innerhalb eines Netzwerks gleichzeitig zu eliminieren, indem eine Reihen-/Parallelanalyse verwendet wird, um Spannungsabfälle (und/oder Ströme) innerhalb des modifizierten Netzwerks für jede Stromquelle separat zu bestimmen. Nachdem die Spannungsabfälle und/oder Ströme für jede separat arbeitende Stromquelle bestimmt wurden, werden die Werte alle übereinander „überlagert“ (algebraisch addiert), um die tatsächlichen Spannungsabfälle/-ströme bei allen aktiven Quellen zu ermitteln. Schauen wir uns unsere Beispielschaltung noch einmal an und wenden wir den Superpositionssatz darauf an:

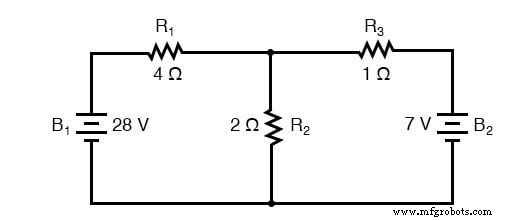
Da wir in dieser Schaltung zwei Stromquellen haben, müssen wir zwei Wertesätze für Spannungsabfälle und/oder Ströme berechnen, eine für die Schaltung mit nur der 28-Volt-Batterie. . .

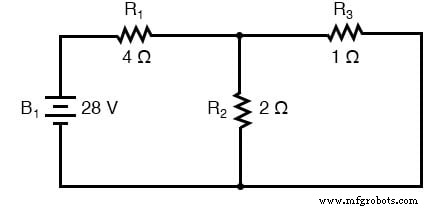
. . . und eine für die Schaltung mit nur der 7-Volt-Batterie in Kraft:

Beim Neuzeichnen des Stromkreises für die Serien-/Parallelanalyse mit einer Quelle werden alle anderen Spannungsquellen durch Drähte (Kurzschlüsse) und alle Stromquellen mit offenen Stromkreisen (Unterbrechungen) ersetzt. Da wir in unserer Beispielschaltung nur Spannungsquellen (Batterien) haben, werden wir jede inaktive Quelle während der Analyse durch einen Draht ersetzen.

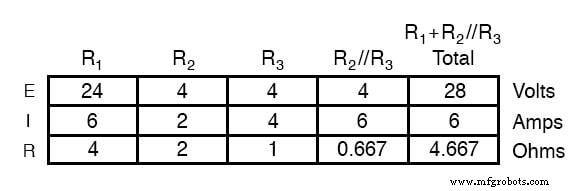
Wenn wir die Schaltung nur mit der 28-Volt-Batterie analysieren, erhalten wir folgende Werte für Spannung und Strom:

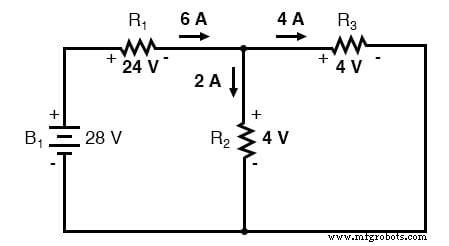
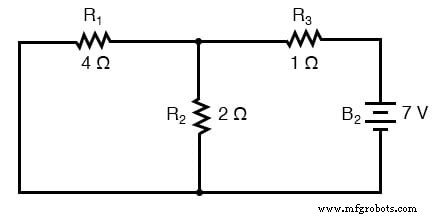
Wenn wir die Schaltung nur mit der 7-Volt-Batterie analysieren, erhalten wir einen weiteren Satz von Werten für Spannung und Strom:

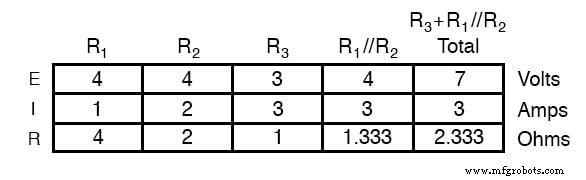
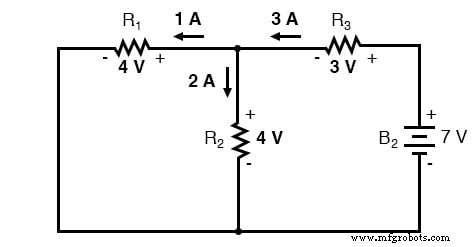
Durch Überlagerung

Bei der Überlagerung dieser Werte von Spannung und Strom müssen wir sehr genau auf Polarität (des Spannungsabfalls) und Richtung (des Stromflusses) achten, da die Werte algebraisch addiert werden müssen .

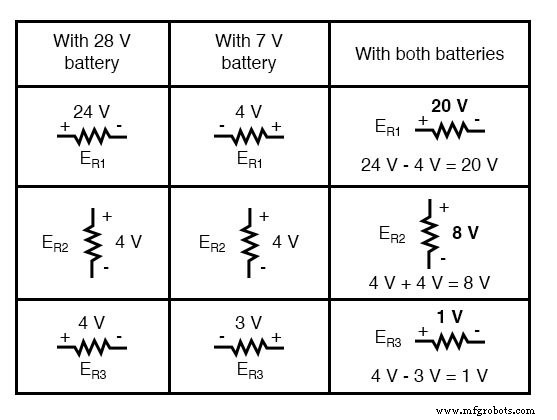
Anwenden dieser überlagerten Spannungswerte auf die Schaltung sieht das Endergebnis etwa so aus:

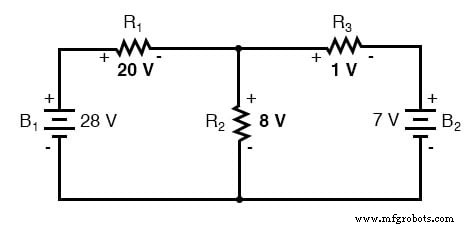
Auch Ströme addieren sich algebraisch und können entweder wie mit den Widerstandsspannungsabfällen überlagert oder einfach aus den Endspannungsabfällen und den jeweiligen Widerständen (I=E/R) berechnet werden. In jedem Fall werden die Antworten die gleichen sein. Hier zeige ich die auf Strom angewendete Superpositionsmethode:

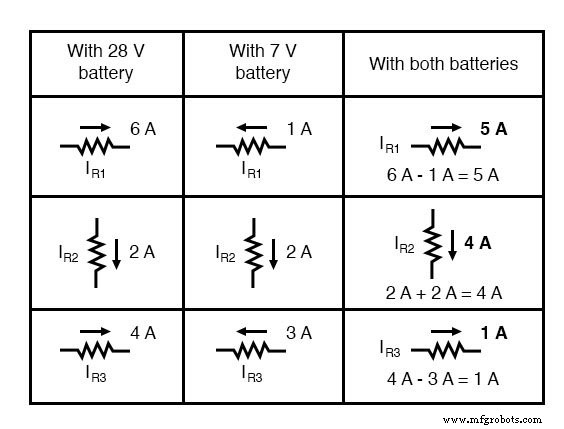
Wenden Sie diese überlagerten Zahlen noch einmal auf unsere Schaltung an:

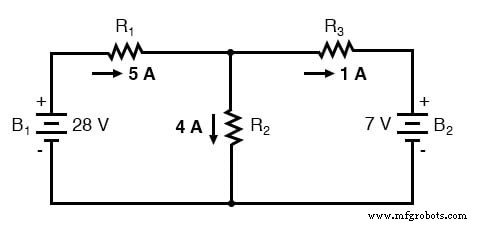
Voraussetzungen für den Superpositionssatz

Ganz schlicht und elegant, finden Sie nicht? Es muss jedoch beachtet werden, dass das Superpositionstheorem nur für Schaltungen funktioniert, die für jede der Stromquellen gleichzeitig auf Serien-/Parallelkombinationen reduzierbar sind (dieses Theorem ist daher für die Analyse einer unsymmetrischen Brückenschaltung nutzlos) und nur funktioniert, wenn die zugrunde liegenden Gleichungen linear sind (keine mathematischen Potenzen oder Wurzeln). Das Erfordernis der Linearität bedeutet, dass das Superpositionstheorem nur für die Bestimmung von Spannung und Strom anwendbar ist, nicht die Leistung!!! Verlustleistung, da es sich um nichtlineare Funktionen handelt, trägt algebraisch nicht zu einer genauen Summe bei, wenn nur eine Quelle gleichzeitig betrachtet wird. Die Notwendigkeit der Linearität bedeutet auch, dass dieses Theorem nicht in Schaltungen angewendet werden kann, in denen sich der Widerstand einer Komponente mit der Spannung oder dem Strom ändert. Daher konnten Netzwerke mit Komponenten wie Lampen (Glühlampen oder Gasentladungen) oder Varistoren nicht analysiert werden.

Eine weitere Voraussetzung für das Superpositionstheorem ist, dass alle Komponenten „bilateral“ sein müssen, das heißt, sie verhalten sich gleich, wenn Elektronen in beide Richtungen durch sie hindurchfließen. Widerstände haben kein polaritätsspezifisches Verhalten, daher erfüllen die bisher untersuchten Schaltungen alle dieses Kriterium.

Das Superpositionstheorem findet Anwendung bei der Untersuchung von Wechselstromkreisen (AC) und Halbleiterschaltungen (Verstärker), wo manchmal Wechselstrom oft mit Gleichstrom gemischt (überlagert) wird. Da Wechselspannungs- und Stromgleichungen (Ohmsches Gesetz) genau wie Gleichstrom linear sind, können wir Superposition verwenden, um die Schaltung nur mit der Gleichstromquelle und dann nur mit der Wechselstromquelle zu analysieren und die Ergebnisse zu kombinieren, um zu sagen, was mit Wechselstrom und . passieren wird Gleichstromquellen in Kraft. Für den Moment reicht Superposition jedoch aus, um eine Pause davon zu machen, simultane Gleichungen durchführen zu müssen, um eine Schaltung zu analysieren.

RÜCKBLICK:

• Das Superpositionstheorem besagt, dass eine Schaltung mit jeweils nur einer Stromquelle analysiert werden kann, wobei die entsprechenden Komponentenspannungen und -ströme algebraisch addiert werden, um herauszufinden, was sie mit allen effektiven Stromquellen tun.
• Um alle außer einer Stromquelle für die Analyse zu negieren, ersetzen Sie jede Spannungsquelle (Batterien) durch einen Draht; Ersetzen Sie eine beliebige Stromquelle durch eine offene (Unterbrechung).

VERWANDTES ARBEITSBLATT:

• Superpositionssatz-Arbeitsblatt