Serien-Widerstands-Kondensator-Schaltungen
Im letzten Abschnitt haben wir gelernt, was in einfachen Wechselstromkreisen nur mit Widerständen und nur mit Kondensatoren passieren würde. Jetzt werden wir die beiden Komponenten in Serienform miteinander kombinieren und die Auswirkungen untersuchen.
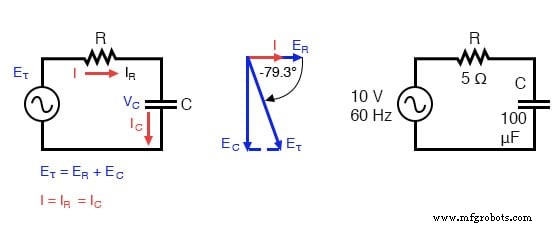
Serienkondensatorschaltung:Spannung eilt dem Strom um 0° bis 90° nach.
Impedanzberechnung
Der Widerstand bietet unabhängig von der Frequenz einen Widerstand von 5 Ω gegen Wechselstrom, während der Kondensator eine Reaktanz von 26,5258 Ω gegen Wechselstrom bei 60 Hz bietet.
Da der Widerstand des Widerstands eine reelle Zahl ist (5 Ω ∠ 0° oder 5 + j0 Ω) und die Reaktanz des Kondensators eine imaginäre Zahl ist (26,5258 Ω ∠ -90° oder 0 - j26,5258 Ω), ergibt sich der kombinierte Effekt der beiden Komponenten ist ein Gegensatz zum Strom gleich der komplexen Summe der beiden Zahlen.
Der Begriff für diesen komplexen Gegensatz zum Strom ist Impedanz , sein Symbol ist Z, und es wird auch in der Einheit Ohm ausgedrückt, genau wie Widerstand und Reaktanz. Im obigen Beispiel beträgt die Gesamtimpedanz des Stromkreises:

Die Impedanz hängt wie erwartet mit Spannung und Strom zusammen, ähnlich dem Widerstand im Ohmschen Gesetz:

Tatsächlich ist dies eine weitaus umfassendere Form des Ohmschen Gesetzes als das, was in der Gleichstromelektronik (E=IR) gelehrt wurde, genauso wie die Impedanz ein weitaus umfassenderer Ausdruck des Widerstands gegen den Elektronenfluss ist als der einfache Widerstand. Jeder Widerstand und jede Reaktanz, einzeln oder in Kombination (seriell/parallel), kann und sollte als einzelne Impedanz dargestellt werden.
Aktuelle Berechnung
Um den Strom in der obigen Schaltung zu berechnen, müssen wir zunächst eine Phasenwinkelreferenz für die Spannungsquelle angeben, die im Allgemeinen mit Null angenommen wird. (Die Phasenwinkel der ohmschen und kapazitiven Impedanz sind immer 0° bzw. -90°, unabhängig von den gegebenen Phasenwinkeln für Spannung oder Strom.)
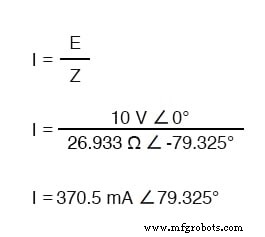
Wie bei der rein kapazitiven Schaltung eilt die Stromwelle der Spannungswelle (der Quelle) voraus, obwohl die Differenz diesmal 79,325° anstatt volle 90° beträgt.
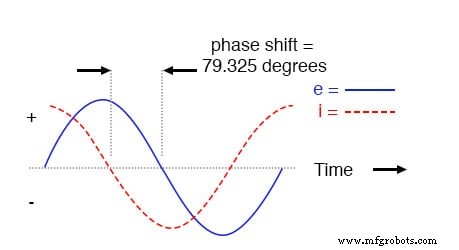
Spannung eilt dem Strom (der Strom eilt der Spannung) in einer R-C-Reihenschaltung nach.
Tabellenmethode
Wie wir im Kapitel AC-Induktivität erfahren haben, ist die „Tabellen“-Methode zum Organisieren von Schaltungsgrößen ein sehr nützliches Werkzeug für die AC-Analyse ebenso wie für die DC-Analyse. Lassen Sie uns bekannte Zahlen für diese Reihenschaltung in eine Tabelle stellen und die Analyse mit diesem Tool fortsetzen:
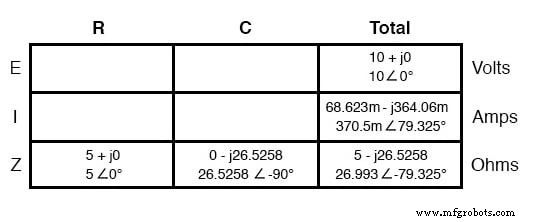
Der Strom in einer Reihenschaltung wird von allen Komponenten zu gleichen Teilen geteilt, sodass die Zahlen in der Spalte „Gesamt“ für Strom auch auf alle anderen Spalten verteilt werden können:
Wenn wir unsere Analyse fortsetzen, können wir das Ohmsche Gesetz (E=IR) vertikal anwenden, um die Spannung über dem Widerstand und dem Kondensator zu bestimmen:
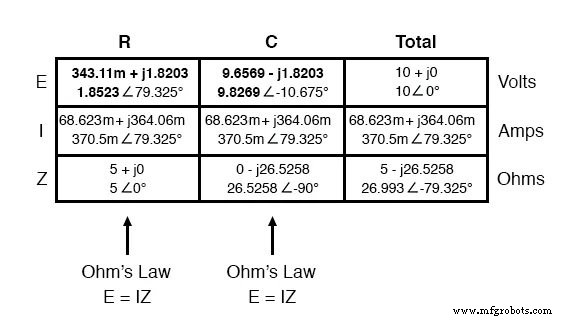
Beachten Sie, dass die Spannung am Widerstand genau den gleichen Phasenwinkel hat wie der Strom durch ihn, was uns sagt, dass E und I in Phase sind (nur für den Widerstand). Die Spannung am Kondensator hat einen Phasenwinkel von -10,675°, genau 90° weniger als der Phasenwinkel des Stromkreises. Dies sagt uns, dass Spannung und Strom des Kondensators immer noch um 90° phasenverschoben sind.
Berechnungen mit SPICE
Lassen Sie uns unsere Berechnungen mit SPICE überprüfen:
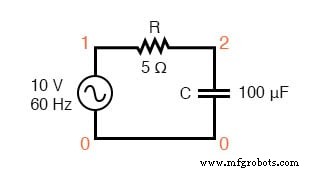
Gewürzschaltung:R-C.

Wieder druckt SPICE verwirrenderweise den aktuellen Phasenwinkel mit einem Wert gleich dem realen Phasenwinkel plus 180° (oder minus 180°).
Es ist jedoch einfach, diese Zahl zu korrigieren und zu überprüfen, ob unsere Arbeit richtig ist. In diesem Fall entspricht die Ausgabe von -100,7° von SPICE für den aktuellen Phasenwinkel positiven 79,3°, was unserem zuvor berechneten Wert von 79,325° entspricht.
Auch hier muss betont werden, dass die berechneten Werte, die realen Spannungs- und Strommessungen entsprechen, die in polaren sind Form, nicht rechteckige Form!
Wenn wir beispielsweise diese Reihenwiderstand-Kondensator-Schaltung tatsächlich aufbauen und die Spannung am Widerstand messen würden, würde unser Voltmeter 1,8523 . anzeigen Volt, nicht 343,11 Millivolt (real rechteckig) oder 1,8203 Volt (imaginär rechteckig).
Reale Instrumente, die an reale Stromkreise angeschlossen sind, liefern Angaben, die der Vektorlänge (Größe) der berechneten Zahlen entsprechen. Während die rechteckige Form der Notation komplexer Zahlen für die Durchführung von Addition und Subtraktion nützlich ist, ist sie eine abstraktere Form der Notation als die Polare, die allein den wahren Messungen direkt entspricht.
Die Impedanz (Z) einer R-C-Reihenschaltung kann berechnet werden, wenn der Widerstand (R) und die kapazitive Reaktanz (XC ). Da E=IR, E=IXC , und E =IZ, Widerstand, Reaktanz und Impedanz sind jeweils proportional zur Spannung. Somit kann das Spannungszeigerdiagramm durch ein ähnliches Impedanzdiagramm ersetzt werden.
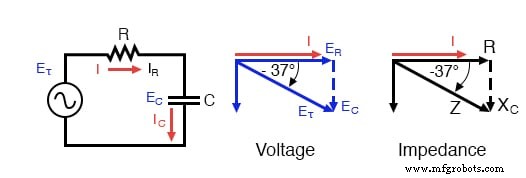
Serie:R-C-Schaltung Impedanzzeigerdiagramm.
Beispiel: Gegeben:Ein 40--Widerstand in Reihe mit einem 88,42-Mikrofarad-Kondensator. Finden Sie die Impedanz bei 60 Hertz.
RÜCKBLICK:
- Impedanz ist das Gesamtmaß des Widerstands gegen elektrischen Strom und ist die komplexe (Vektor-)Summe aus („realem“) Widerstand und („imaginärer“) Reaktanz.
- Impedanzen (Z) werden wie Widerstände (R) in der Reihenschaltungsanalyse verwaltet:Reihenimpedanzen addieren sich zur Gesamtimpedanz. Führen Sie nur alle Berechnungen in komplexer (nicht skalarer) Form durch! ZGesamt1 + Z2 + . . . Zn
- Bitte beachten Sie, dass sich Impedanzen immer in Reihe addieren, unabhängig davon, aus welcher Art von Komponenten die Impedanzen bestehen. Das heißt, Widerstandsimpedanz, induktive Impedanz und kapazitive Impedanz sind mathematisch gleich zu behandeln.
- Eine rein ohmsche Impedanz hat immer einen Phasenwinkel von genau 0° (ZR =R Ω ∠ 0°).
- Eine rein kapazitive Impedanz hat immer einen Phasenwinkel von genau -90° (ZC =XC Ω ∠ -90°).
- Ohmsches Gesetz für Wechselstromkreise:E =IZ; ich =E/Z; Z =E/I
- Wenn Widerstände und Kondensatoren in Schaltkreisen zusammengemischt werden, hat die Gesamtimpedanz einen Phasenwinkel zwischen 0°- und -90°.
VERWANDTE ARBEITSBLÄTTER:
- Arbeitsblatt für Reihen- und Parallel-Wechselstromkreise
Industrietechnik



