Resonanzfilter

Bisher haben die Filterdesigns, auf die wir uns konzentriert haben, entweder . verwendet Kondensatoren oder Induktivitäten, aber nie beides gleichzeitig. Wir sollten jetzt wissen, dass Kombinationen von L und C dazu neigen, mitzuschwingen, und diese Eigenschaft kann beim Entwerfen von Bandpass- und Bandsperrfilterschaltungen ausgenutzt werden.

Reihen-LC-Schaltungen ergeben eine minimale Impedanz bei Resonanz, während parallele LC-Schaltungen ("Tank") eine maximale Impedanz bei ihrer Resonanzfrequenz ergeben. Da wir dies wissen, haben wir zwei grundlegende Strategien zum Entwerfen von Bandpass- oder Bandsperrenfiltern.

Bei Bandpassfiltern sind die beiden grundlegenden Resonanzstrategien folgende:Reihen-LC, um ein Signal durchzulassen, oder parallele LC, um ein Signal kurzzuschließen. Die beiden Schemata werden hier gegenübergestellt und simuliert:

Resonanter Bandpassfilter der Serie

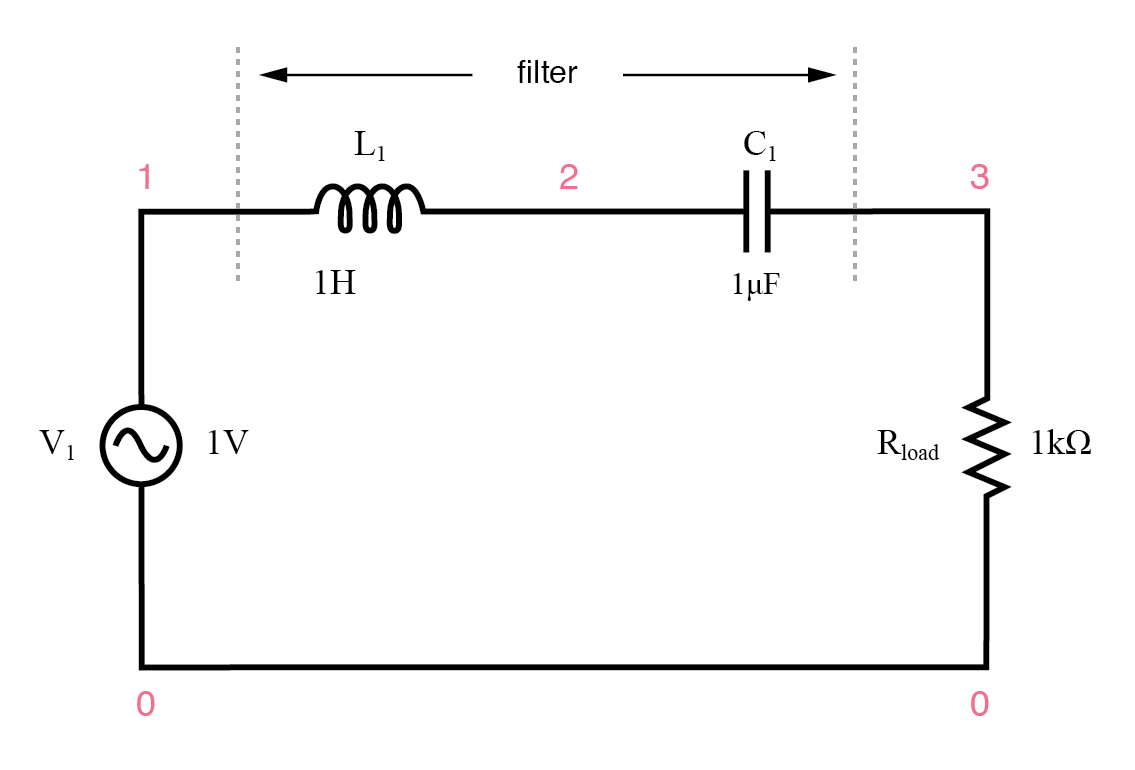
Resonanter LC-Bandpassfilter der Serie.

Die LC-Komponenten der Serie lassen das Signal bei Resonanz durch und blockieren Signale anderer Frequenzen daran, die Last zu erreichen.

resonanter Bandpassfilter der Serie v1 1 0 ac 1 sin l1 1 2 1 c1 2 3 1u rload 3 0 1k .ac lin 20 50 250 .plot ac v(3) .Ende 

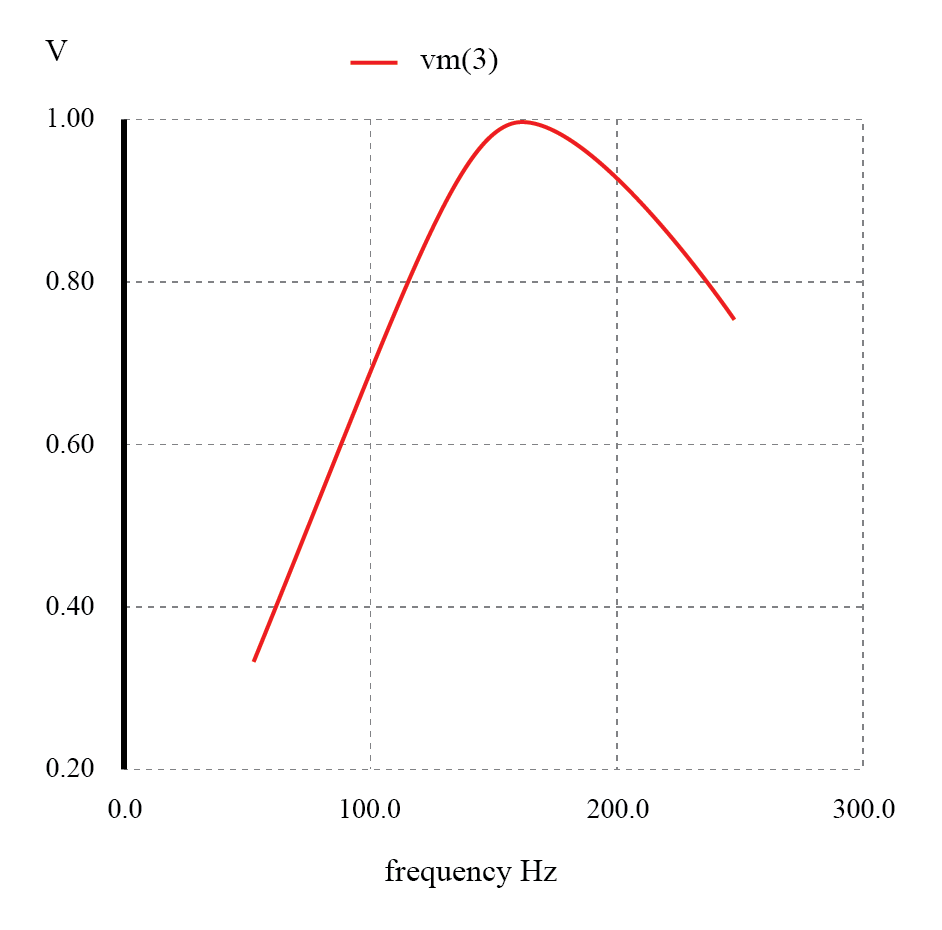
Resonanter Bandpassfilter der Serie:Spannungsspitzen bei einer Resonanzfrequenz von 159,15 Hz.

Einige Punkte, die Sie beachten sollten:Sehen Sie, dass es im Gegensatz zu Bandpassfiltern, die nur aus Kondensatoren oder Induktivitäten bestehen, praktisch keine Signaldämpfung innerhalb des „Durchlassbandes“ (dem Frequenzbereich nahe der Lastspannungsspitze) gibt.

Da dieses Filter nach dem Prinzip der Reihen-LC-Resonanz arbeitet, deren Resonanzfrequenz nicht vom Schaltungswiderstand beeinflusst wird, wird der Wert des Lastwiderstands die Spitzenfrequenz nicht verzerren. Andere Werte für den Lastwiderstand werden jedoch Ändern Sie die „Steilheit“ des Bode-Plots (die „Selektivität“ des Filters).

Der andere grundlegende Stil von resonanten Bandpassfiltern verwendet einen Schwingkreis (parallele LC-Kombination), um Signale mit zu hoher oder zu niedriger Frequenz vom Erreichen der Last kurzzuschließen:

Parallel-resonanter Bandpassfilter

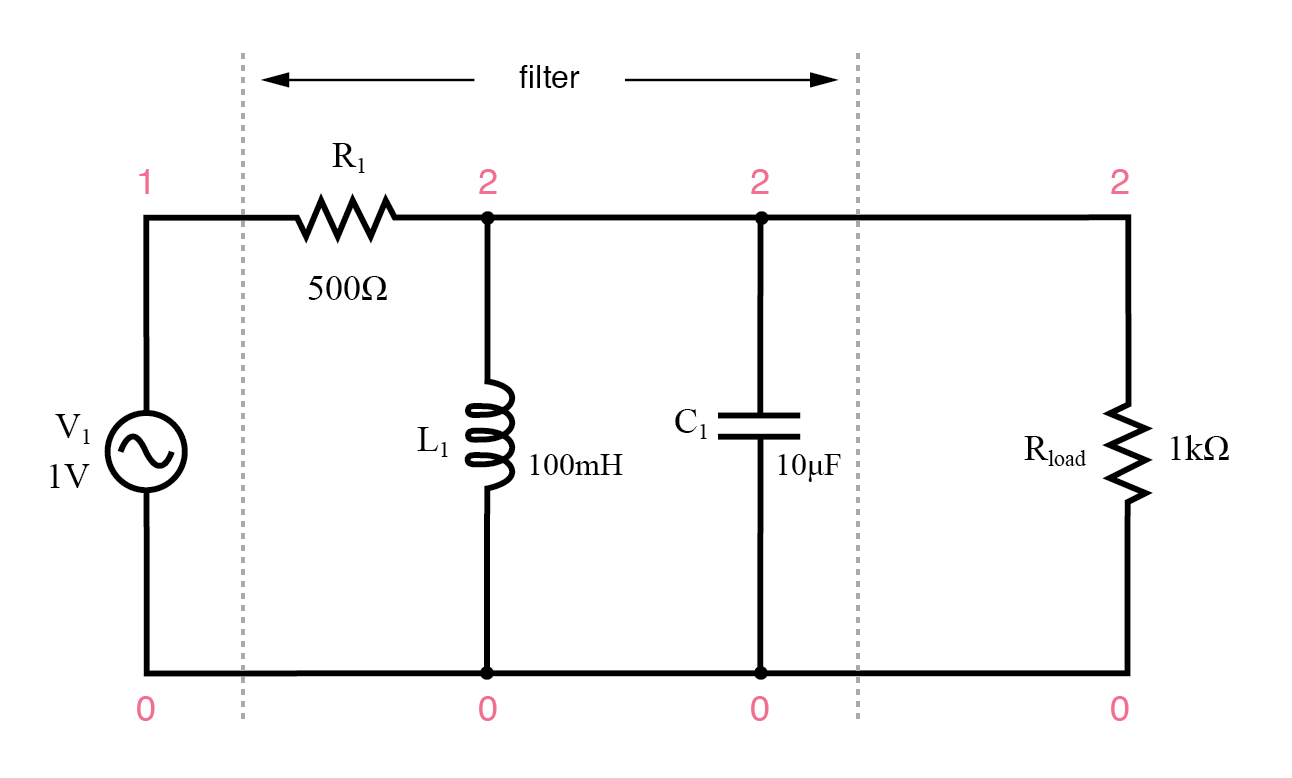
Parallel-resonanter Bandpassfilter.

Der Schwingkreis hat bei Resonanz eine hohe Impedanz, sodass das Signal mit minimaler Dämpfung zur Last gelangen kann. Unter oder über der Resonanzfrequenz hat der Schwingkreis jedoch eine niedrige Impedanz, wodurch das Signal kurzgeschlossen wird und das meiste davon über den Reihenwiderstand R₁ . fällt .

paralleler resonanter Bandpassfilter v1 1 0 ac 1 sin r1 1 2 500 l1 2 0 100m c1 2 0 10u rLast 2 0 1k .ac lin 20 50 250 .plot ac v(2) .Ende 

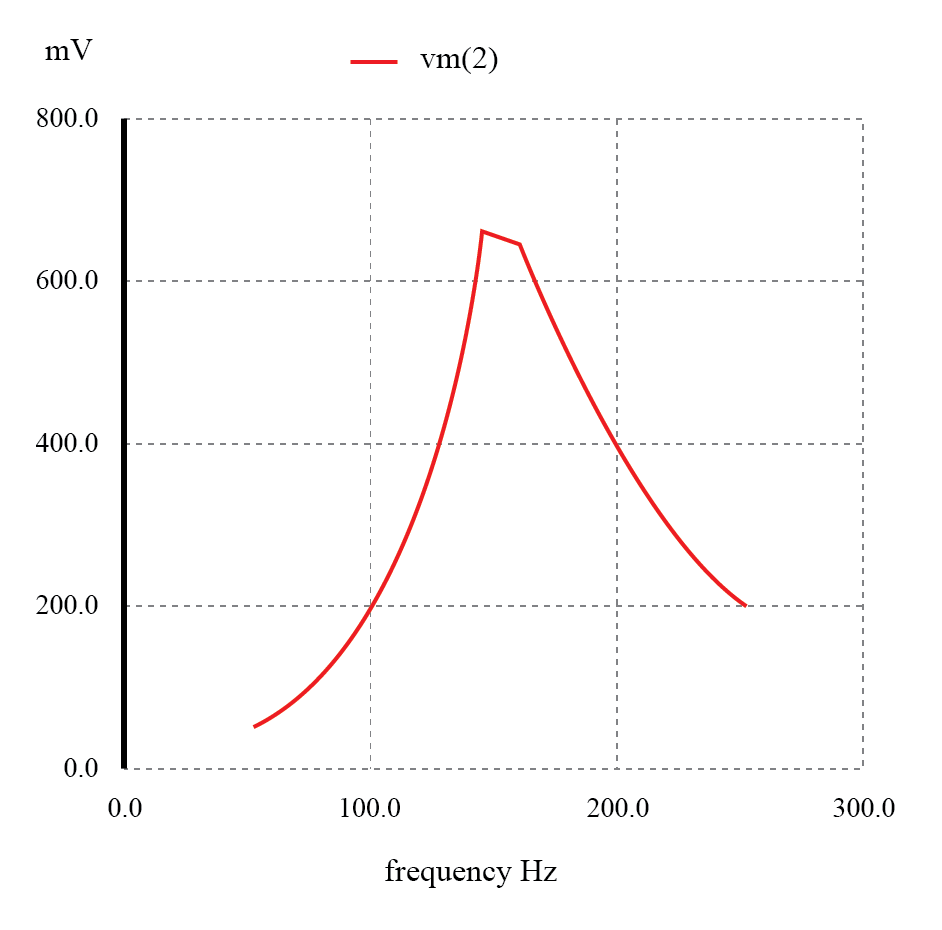
Parallel-Resonanzfilter:Spannungsspitzen einer Resonanzfrequenz von 159,15 Hz.

Genau wie die Tiefpass- und Hochpassfilterdesigns, die auf einem Serienwiderstand und einer parallelen „Kurzschlusskomponente“ beruhen, um unerwünschte Frequenzen zu dämpfen, kann dieser Resonanzkreis niemals die volle Eingangsspannung (Quellenspannung) an die Last liefern.

Dieser Serienwiderstand wird immer eine gewisse Spannung abfallen, solange ein Lastwiderstand an den Ausgang des Filters angeschlossen ist. Es sollte beachtet werden, dass diese Form der Bandpassfilterschaltung in analogen Radioabstimmschaltungen sehr beliebt ist, um eine bestimmte Radiofrequenz aus der Vielzahl von Frequenzen auszuwählen, die von der Antenne verfügbar sind.

In den meisten analogen Radiotuner-Schaltungen bewegt das Drehrad für die Senderauswahl einen variablen Kondensator in einem Schwingkreis.

Variabler Kondensator stimmt den Schwingkreis des Radioempfängers ab, um einen von vielen Sendern auszuwählen.

Der variable Kondensator und die Luftspule, die in der obigen Abbildung eines einfachen Radios gezeigt werden, umfassen die Hauptelemente im Schwingkreisfilter, der verwendet wird, um das Signal eines Radiosenders von einem anderen zu unterscheiden.

So wie wir Reihen- und Parallel-LC-Schwingkreise verwenden können, um nur diese Frequenzen innerhalb eines bestimmten Bereichs durchzulassen, können wir sie auch verwenden, um Frequenzen innerhalb eines bestimmten Bereichs zu blockieren, wodurch ein Bandsperrfilter entsteht. Auch hier haben wir zwei Hauptstrategien zu verfolgen, entweder Serien- oder Parallelresonanz zu verwenden. Zuerst schauen wir uns die Serienvielfalt an:

Resonanter Bandsperrfilter der Serie

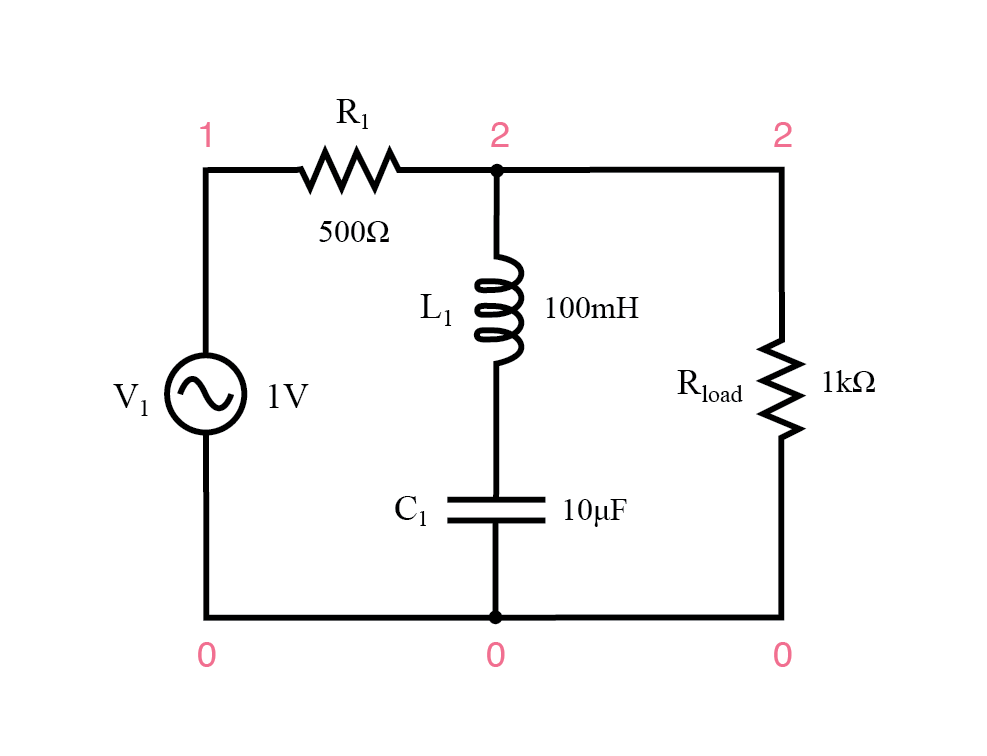
Resonanter Bandsperrfilter der Serie.

Wenn die Reihen-LC-Kombination Resonanz erreicht, schließt ihre sehr niedrige Impedanz das Signal kurz und lässt es über den Widerstand R₁ . fallen und Verhindern des Durchgangs auf die Last.

resonanter Bandsperrfilter der Serie v1 1 0 ac 1 sin r1 1 2 500 l1 2 3 100m c1 3 0 10u rLast 2 0 1k .ac lin 20 70 230 .plot ac v(2) .Ende 

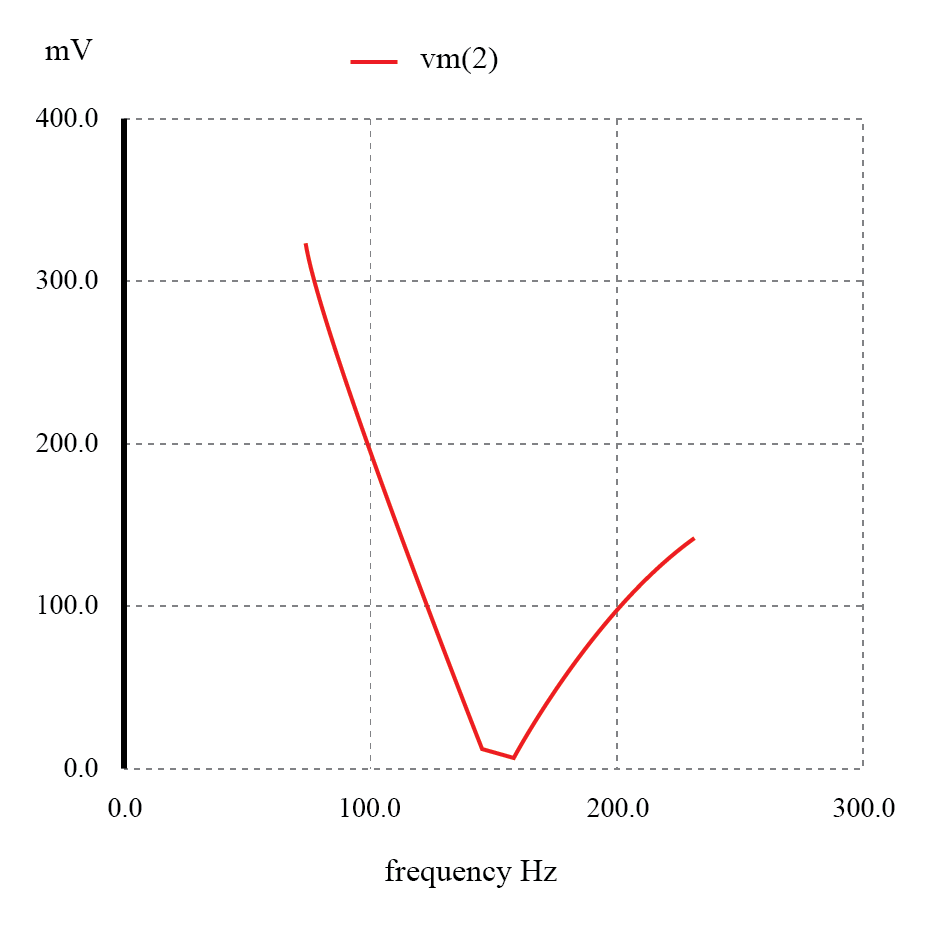
Resonantes Bandsperrfilter der Serie:Notch-Frequenz =LC-Resonanzfrequenz (159,15 Hz).

Als nächstes werden wir das parallelresonante Bandsperrfilter untersuchen:

Parallel-resonanter Bandsperrfilter

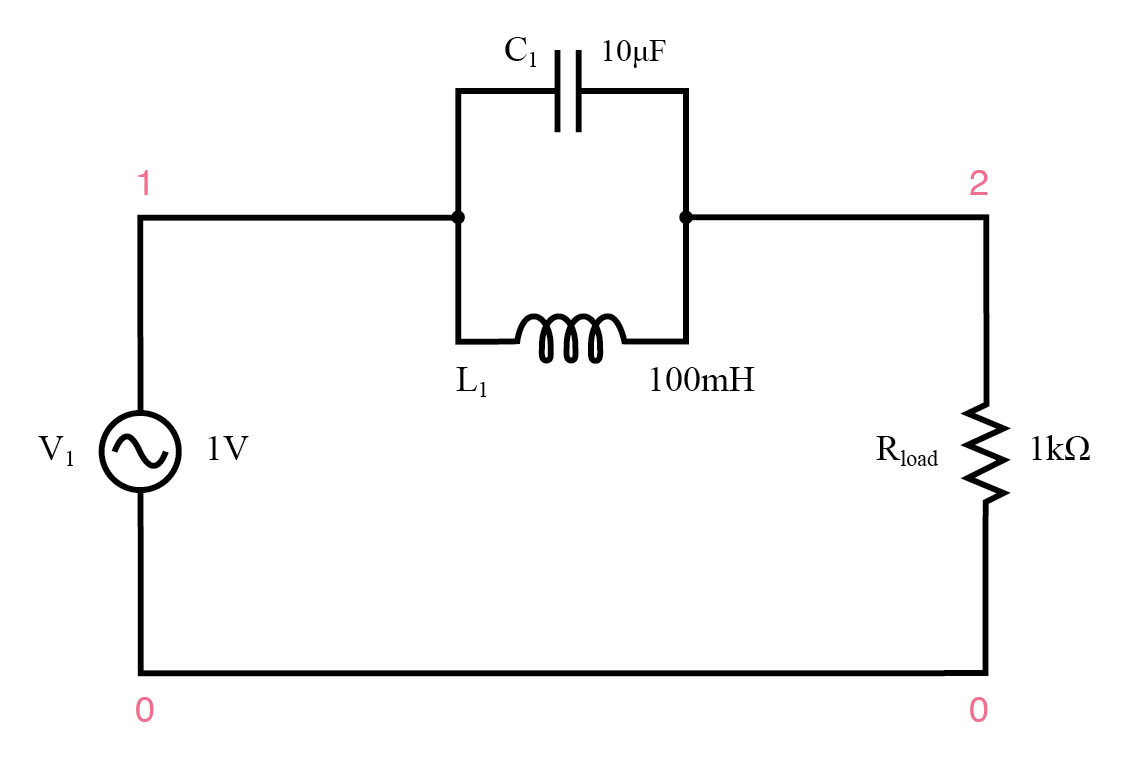
Parallel-resonanter Bandsperrfilter.

Die parallelen LC-Komponenten weisen bei Resonanzfrequenz eine hohe Impedanz auf, wodurch das Signal von der Last bei dieser Frequenz blockiert wird. Umgekehrt gibt es Signale mit anderen Frequenzen an die Last weiter.

paralleler resonanter Bandsperrfilter v1 1 0 ac 1 sin l1 1 2 100m c1 1 2 10u rLast 2 0 1k .ac lin 20 100 200 .plot ac v(2) .Ende 

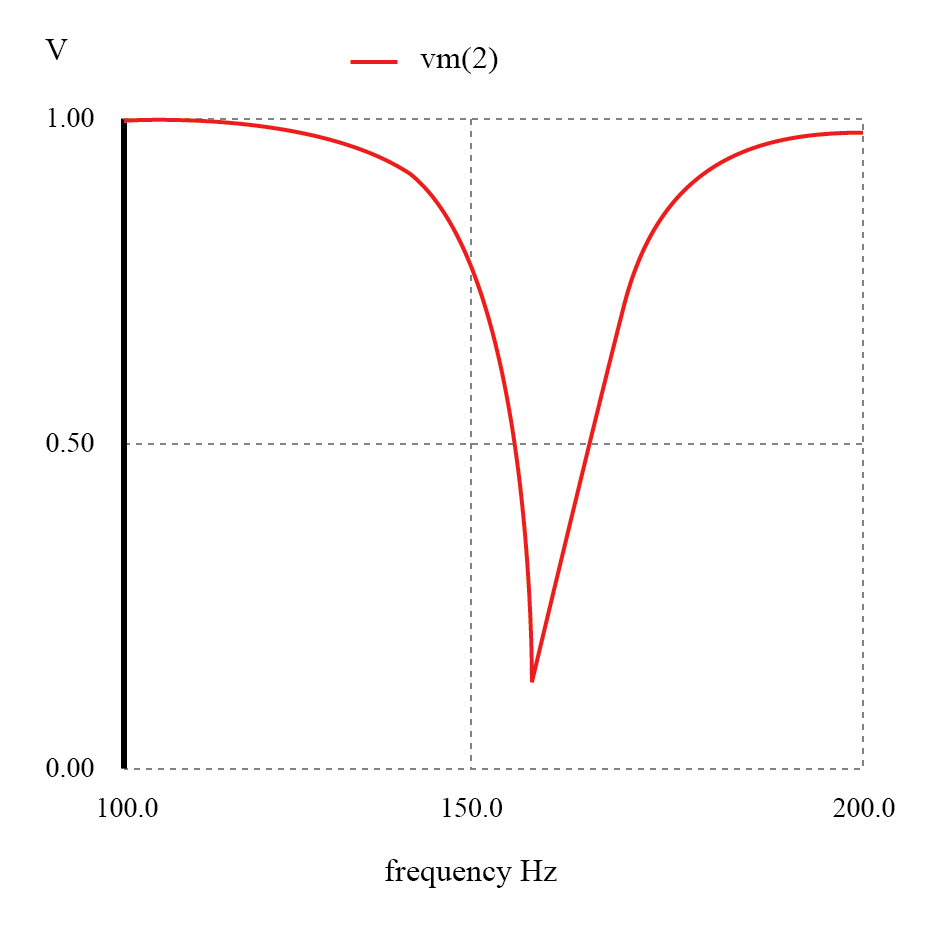
Parallelresonanz-Bandsperre:Notch-Frequenz =LC-Resonanzfrequenz (159,15 Hz).

Beachten Sie noch einmal, wie das Fehlen eines Vorwiderstands für eine minimale Dämpfung für alle gewünschten (durchgelassenen) Signale sorgt. Die Amplitude bei der Kerbfrequenz ist dagegen sehr gering. Mit anderen Worten, dies ist ein sehr „selektiver“ Filter.

Bei all diesen Resonanzfilterdesigns hängt die Selektivität stark von der „Reinheit“ der verwendeten Induktivität und Kapazität ab. Wenn ein Streuwiderstand vorhanden ist (besonders wahrscheinlich in der Induktivität), verringert dies die Fähigkeit des Filters, Frequenzen fein zu unterscheiden, und führt antiresonante Effekte ein, die die Spitzen-/Kerbfrequenz verzerren.

Ein Wort der Vorsicht an diejenigen, die Tiefpass- und Hochpassfilter entwickeln, ist an dieser Stelle angebracht. Nach der Bewertung der standardmäßigen RC- und LR-Tiefpass- und Hochpassfilter-Designs könnte einem Studenten einfallen, dass ein besseres und effektiveres Design von Tiefpass- oder Hochpassfiltern realisiert werden könnte, indem kapazitive und induktive Elemente miteinander kombiniert werden, wie z die Abbildung unten.

Kapazitiver induktiver Tiefpassfilter

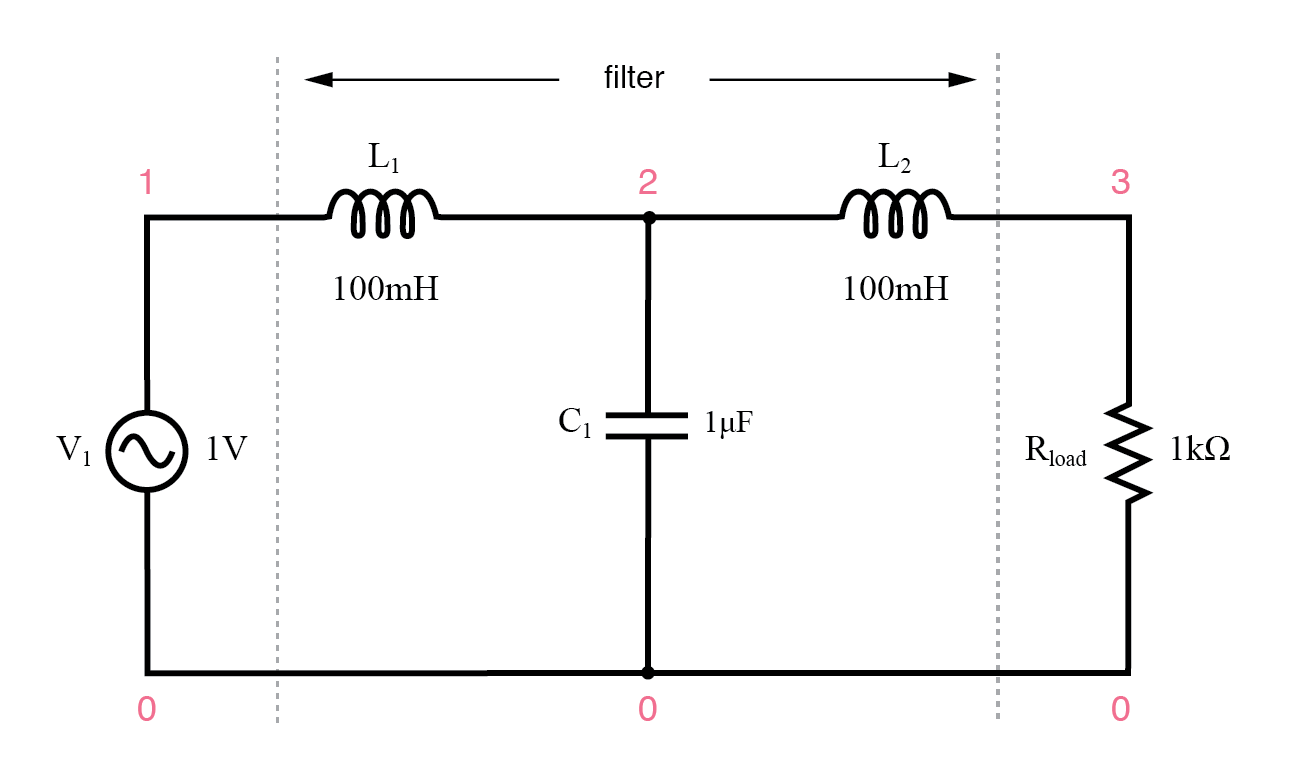
Kapazitiver induktiver Tiefpassfilter.

Die Induktivitäten sollten alle hohen Frequenzen blockieren, während der Kondensator auch alle hohen Frequenzen kurzschließen sollte. Beide arbeiten zusammen, damit nur niederfrequente Signale die Last erreichen.

Dies scheint zunächst eine gute Strategie zu sein und macht einen Serienwiderstand überflüssig. Der aufschlussreichere Schüler wird jedoch erkennen, dass jede Kombination von Kondensatoren und Induktoren zusammen in einem Stromkreis wahrscheinlich Resonanzeffekte bei einer bestimmten Frequenz verursacht.

Resonanz kann, wie wir bereits gesehen haben, zu seltsamen Dingen führen. Lassen Sie uns eine SPICE-Analyse erstellen und sehen, was über einen weiten Frequenzbereich passiert:

LC-Tiefpassfilter v1 1 0 ac 1 sin l1 1 2 100m c1 2 0 1u l2 2 3 100m rload 3 0 1k .ac lin 20 100 1k .plot ac v(3) .Ende 

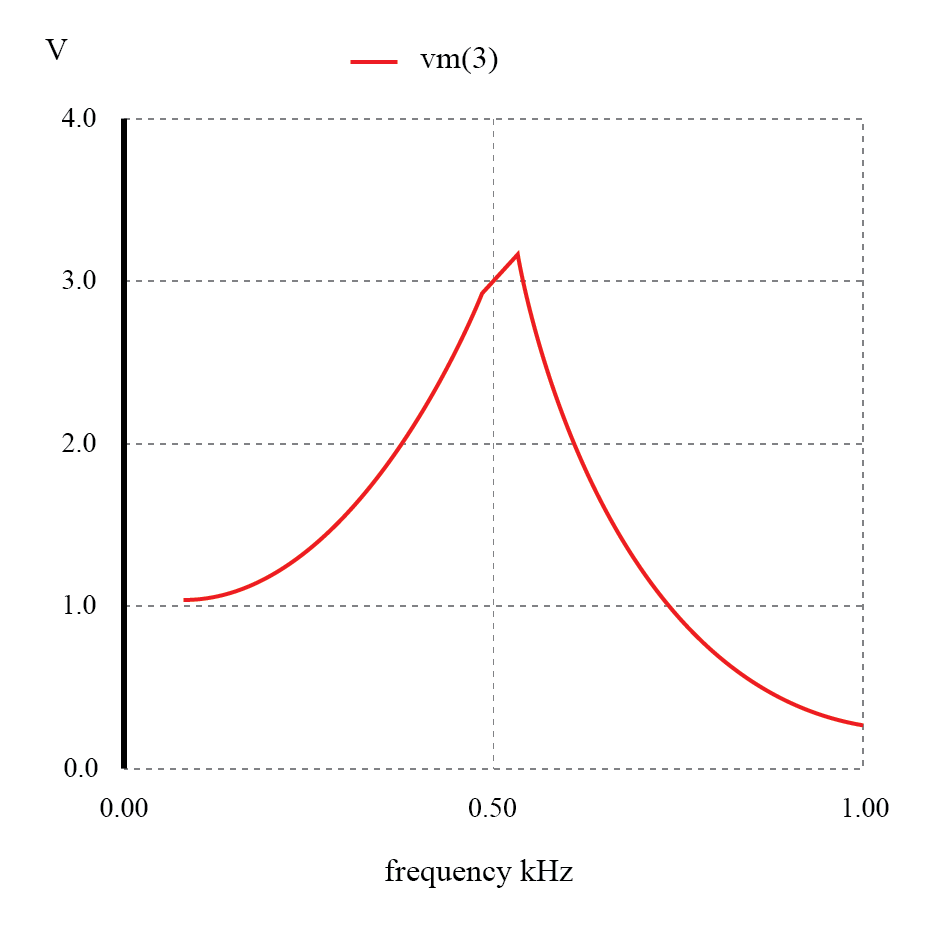
Unerwartete Reaktion des L-C-Tiefpassfilters.

Was ein Tiefpassfilter sein sollte, entpuppt sich als Bandpassfilter mit einer Spitze um die 526 Hz! Die Kapazität und Induktivität in dieser Filterschaltung erreichen an diesem Punkt Resonanz, was einen großen Spannungsabfall um C₁ . erzeugt , die bei der Last zu sehen ist, unabhängig von L₂ dämpfender Einfluss.

Die Ausgangsspannung der Last an diesem Punkt übersteigt tatsächlich die Eingangsspannung (Quellenspannung)! Ein wenig mehr Nachdenken zeigt, dass wenn L₁ und C₂ in Resonanz sind, belasten sie die Wechselstromquelle sehr stark (sehr niedrige Impedanz), was möglicherweise auch nicht gut ist.

Wir führen dieselbe Analyse noch einmal durch, aber dieses Mal zeichnen wir C₁ . die Spannung vm(2) in der Abbildung unten und den Quellenstrom I(v1) zusammen mit der Lastspannung vm(3):

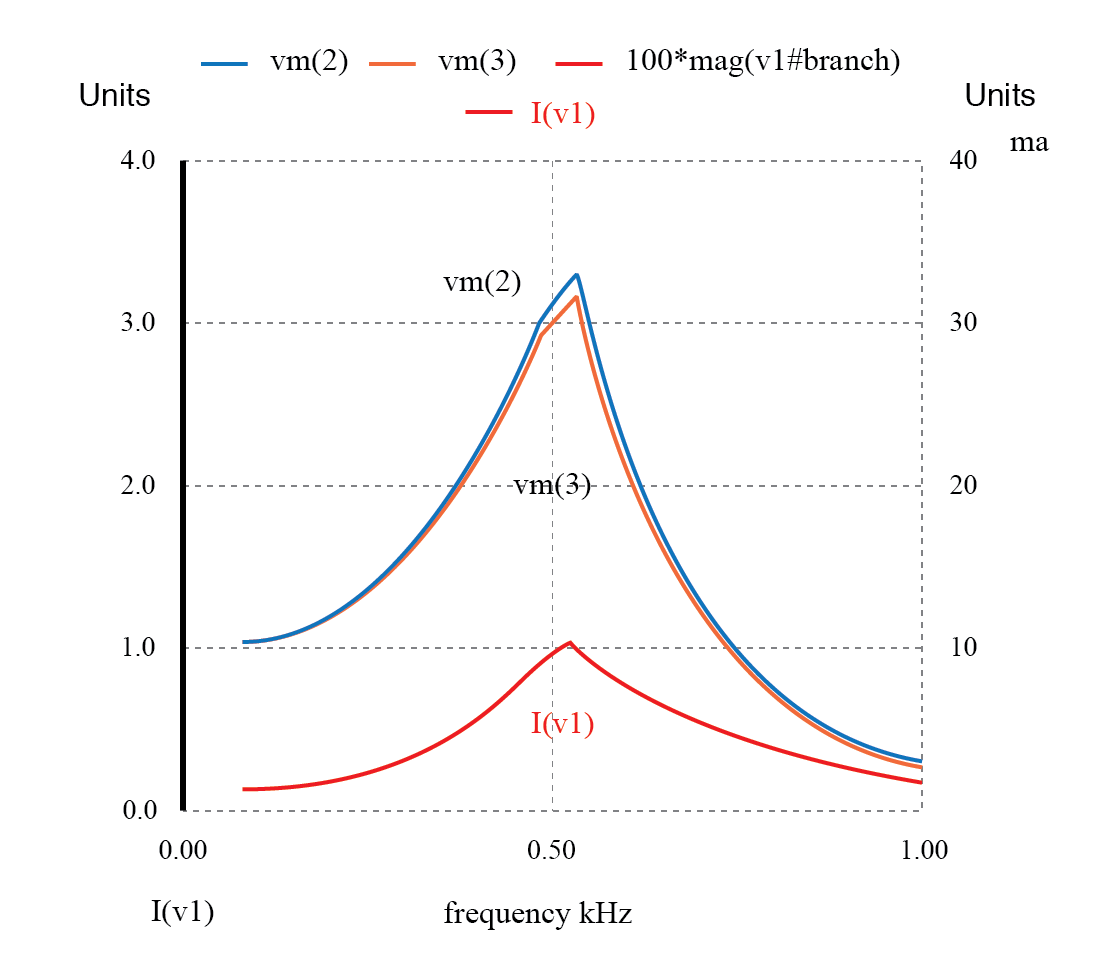
Der Strom steigt bei der unerwünschten Resonanz des L-C-Tiefpassfilters.

Tatsächlich sehen wir die Spannung an C₁ und der Quellenstrom erreicht einen hohen Punkt bei der gleichen Frequenz, wo die Lastspannung maximal ist. Wenn wir von diesem Filter eine einfache Tiefpassfunktion erwarten würden, könnten wir von den Ergebnissen enttäuscht sein.

Das Problem besteht darin, dass ein L-C-Filter eine Eingangsimpedanz und eine Ausgangsimpedanz hat, die angepasst werden müssen. Die Impedanz der Spannungsquelle muss der Eingangsimpedanz des Filters entsprechen und die Ausgangsimpedanz des Filters muss mit „r_load . übereinstimmen ” für eine flache Antwort.

Die Eingangs- und Ausgangsimpedanz ergibt sich aus der Quadratwurzel von (L/C).

Z =(L/C) ^1/2

Aus den Komponentenwerten können wir die Impedanz des Filters und den erforderlichen R_g . ermitteln und R_load passend dazu.

Für L=100 mH, C=1µF Z =(L/C) ^1/2 =((100 mH)/(1 µF)) ^1/2 =316

In der Abbildung unten haben wir R_g . hinzugefügt =316 Ω an den Generator und änderte die Last R_load von 1000 Ω bis 316 Ω. Beachten Sie, dass das L/C-Verhältnis hätte angepasst werden können, um diesem Widerstand zu entsprechen, wenn wir eine Last von 1000 Ω treiben müssten.

Impedanz-angepasster Filter

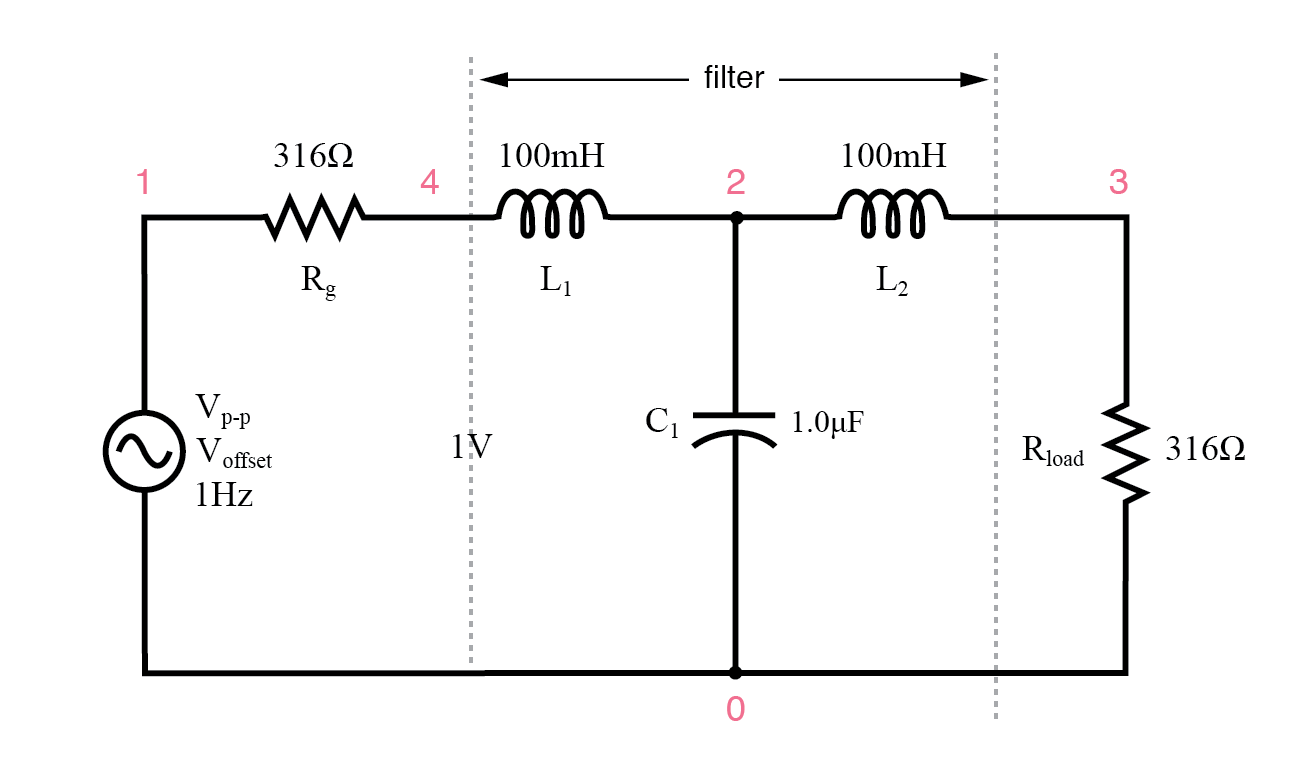
Schaltung der Quelle und des lastangepassten L-C-Tiefpassfilters.

LC-angepasster Tiefpassfilter V1 1 0 ac 1 SIN Rg 1 4 316 L1 4 2 100m C1 2 0 1.0u L2 2 3 100m RLast 3 0 316 .ac lin 20 100 1k .plot ac v(3) .Ende 

Die Abbildung unten zeigt die „flache“ Reaktion des L-C-Tiefpassfilters, wenn die Quellen- und Lastimpedanz mit den Eingangs- und Ausgangsimpedanzen des Filters übereinstimmen.

Die Reaktion des impedanzangepassten L-C-Tiefpassfilters ist bis zur Grenzfrequenz nahezu flach.

Beim Vergleich der Reaktion des unangepassten Filters mit dem angepassten Filter ist darauf hinzuweisen, dass eine variable Belastung des Filters eine beträchtliche Spannungsänderung erzeugt. Diese Eigenschaft ist direkt auf L-C-gefilterte Netzteile anwendbar – die Verordnung ist arm. Die Versorgungsspannung ändert sich mit einer Laständerung. Dies ist unerwünscht.

Diese schlechte Lastregelung kann durch eine Schwingdrossel abgemildert werden . Das ist ein Würge , Induktor, entworfen zum Sättigen wenn ein großer Gleichstrom durch ihn fließt.

Mit gesättigt meinen wir, dass der Gleichstrom einen „zu“ hohen Fluss im Magnetkern erzeugt, sodass die Wechselstromkomponente des Stroms den Fluss nicht verändern kann. Da die Induktion proportional zu dΦ/dt ist, wird die Induktivität durch den starken Gleichstrom verringert.

Die Abnahme der Induktivität verringert die Reaktanz X_L . Eine Verringerung der Reaktanz verringert den Spannungsabfall über der Induktivität; Dadurch wird die Spannung am Filterausgang erhöht. Dies verbessert die Spannungsregelung in Bezug auf variable Lasten.

Trotz der unbeabsichtigten Resonanz werden Tiefpassfilter aus Kondensatoren und Induktivitäten häufig als Endstufen in AC/DC-Netzteilen verwendet, um die unerwünschte AC-„Welligkeit“-Spannung aus dem aus AC umgewandelten DC herauszufiltern.

Warum ist das so, wenn dieses spezielle Filterdesign einen potenziell störenden Resonanzpunkt besitzt?

Die Antwort liegt in der Auswahl der Filterkomponentengrößen und der Frequenzen, die von einem AC/DC-Wandler (Gleichrichter) angetroffen werden. Bei einem AC/DC-Netzteilfilter versuchen wir, die Gleichspannung von einer kleinen Menge relativ hochfrequenter Wechselspannung zu trennen.

Die Filterinduktivitäten und -kondensatoren sind im Allgemeinen ziemlich groß (typisch sind mehrere Henrys für die Induktivitäten und Tausende von µF für die Kondensatoren), wodurch die Resonanzfrequenz des Filters sehr, sehr niedrig ist. DC hat natürlich eine „Frequenz“ von Null, also kann es auf keinen Fall einen LC-Kreis zum Schwingen bringen.

Die Welligkeitsspannung hingegen ist eine nicht-sinusförmige Wechselspannung, die aus einer Grundfrequenz besteht, die mindestens doppelt so hoch ist wie die der umgewandelten Wechselspannung, zusätzlich mit um ein Vielfaches höheren Oberwellen.

Bei Steckernetzteilen, die mit 60 Hz Wechselstrom betrieben werden (60 Hz in den USA; 50 Hz in Europa), beträgt die niedrigste Frequenz, die der Filter jemals sehen wird, 120 Hz (100 Hz in Europa), was weit darüber liegt seinen Resonanzpunkt. Daher wird der potenziell störende Resonanzpunkt in einem solchen Filter vollständig vermieden.

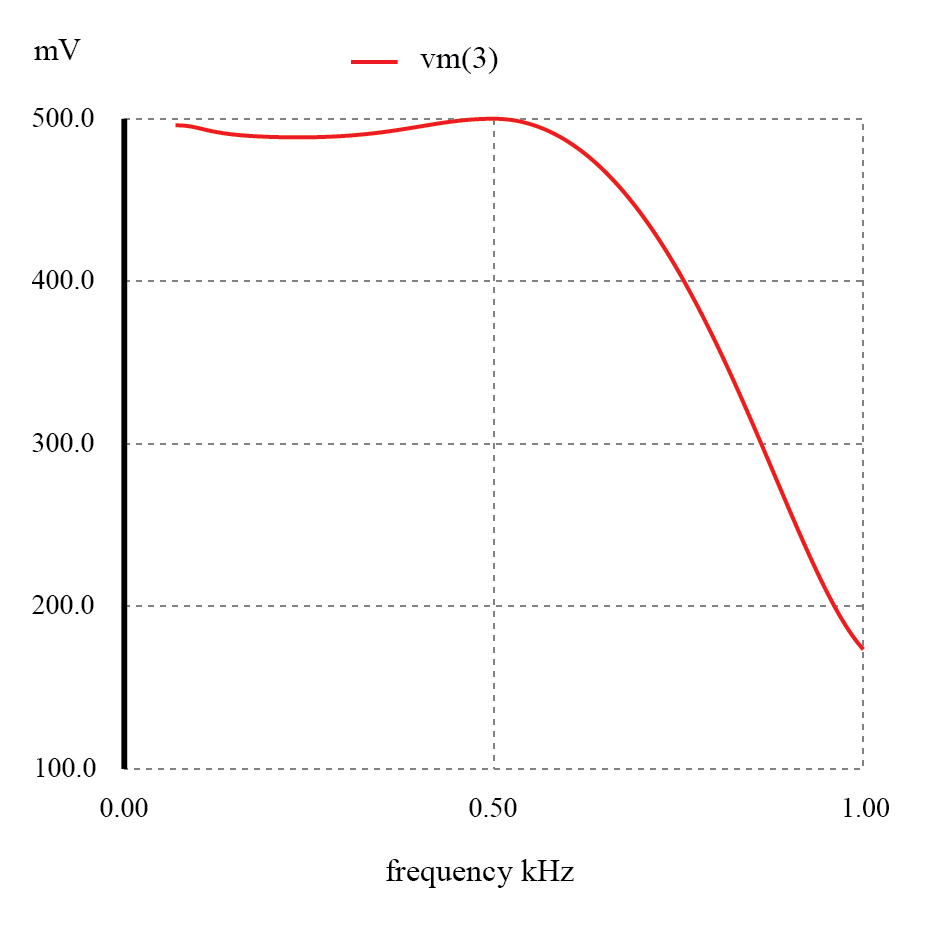
Die folgende SPICE-Analyse berechnet den Spannungsausgang (AC und DC) für einen solchen Filter, wobei DC- und AC-(120-Hz-)Reihenspannungsquellen eine grobe Annäherung an den Mischfrequenzausgang eines AC/DC-Wandlers liefern.

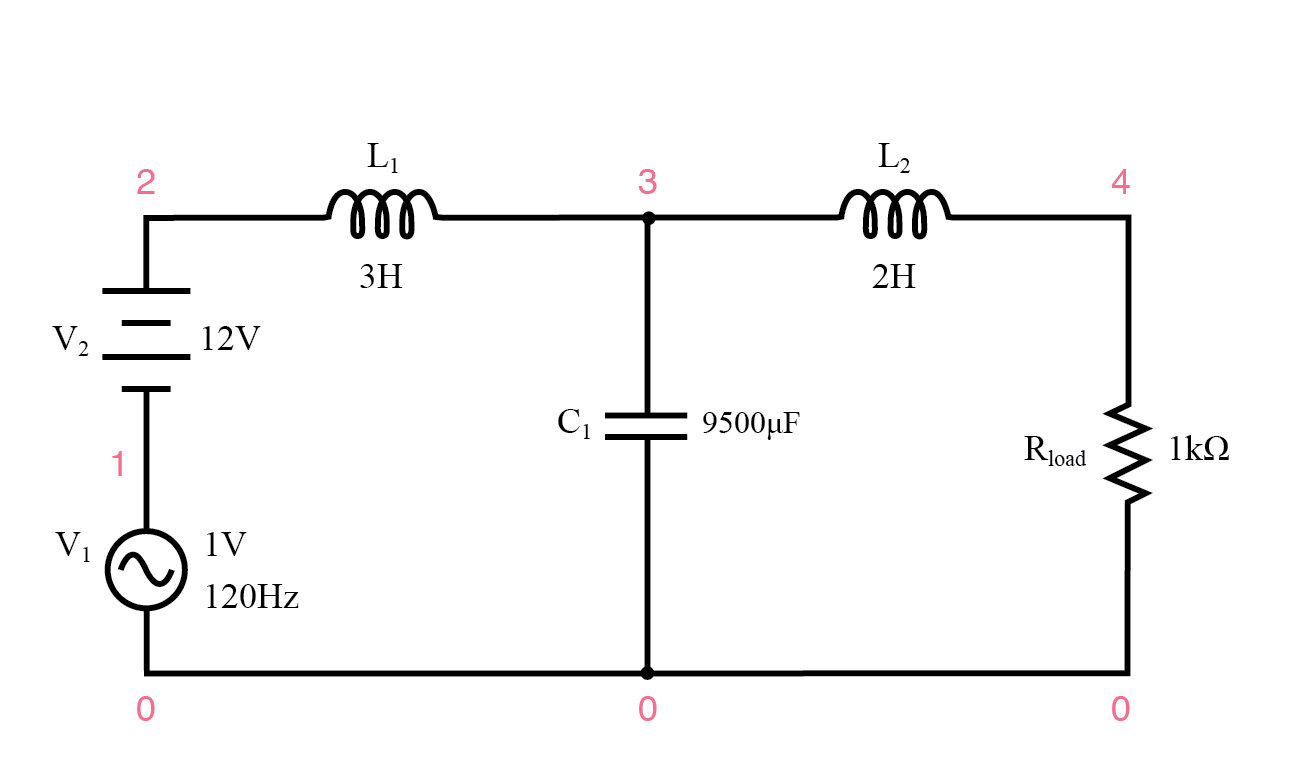
AC/DC-Netzteilfilter bietet "welligkeitsfreien" Gleichstrom.

AC/DC-Netzteilfilter bietet „welligkeitsfreien“ Gleichstrom AC/DC-Netzteilfilter v1 1 0 ac 1 sin v2 2 1 dc l1 2 3 3 c1 3 0 9500u l2 3 4 2 rload 4 0 1k .dc v2 12 12 1 .ac lin 1 120 120 .druck dc v(4) .druck ac v(4) .Ende v2 v(4) 1.200E+01 1.200E+01 Gleichspannung bei Last =12 Volt Frequenz v(4) 1.200E+02 3.412E-05 Wechselspannung bei Last =34.12 Mikrovolt 

Mit vollen 12 Volt Gleichstrom an der Last und nur noch 34,12 µV Wechselstrom von der 1-Volt-Wechselstromquelle, die über die Last gelegt wird, erweist sich dieses Schaltungsdesign als sehr effektiver Stromversorgungsfilter.

Die hier gewonnenen Erkenntnisse über Resonanzeffekte gelten auch für den Entwurf von Hochpassfiltern, die sowohl Kondensatoren als auch Induktivitäten verwenden. Solange die gewünschten und unerwünschten Frequenzen gut zu beiden Seiten des Resonanzpunktes liegen, funktioniert der Filter in Ordnung.

Wenn jedoch ein Signal von signifikanter Größe nahe der Resonanzfrequenz an den Eingang des Filters angelegt wird, passieren seltsame Dinge!

RÜCKBLICK:

• Resonante Kombinationen von Kapazität und Induktivität können verwendet werden, um sehr effektive Bandpass- und Bandsperrfilter zu schaffen, ohne dass ein zusätzlicher Widerstand in einer Schaltung erforderlich ist, der den Durchgang gewünschter Frequenzen verringern würde.

VERWANDTE ARBEITSBLÄTTER:

• Resonanz-Arbeitsblatt
• Arbeitsblatt für passive Filterschaltungen