Untersuchung des nanoskaligen Reibungsverhaltens von Graphen auf Goldsubstraten mittels Molekulardynamik

Hintergrund

Graphen ist eines der vielversprechendsten neuen Materialien für die Anwendung in der Nanoelektronik unter einem breiten Spektrum potenzieller Anwendungen [1,2,3,4,5]. In aktuellen elektronischen Geräten auf Graphenbasis wird Gold häufig für elektrische Kontakte verwendet [6]. Daher spielt die Reibung des Graphen-Gold-Systems eine wichtige Rolle bei der effizienten Herstellung und dem zuverlässigen Betrieb solcher Graphen-Geräte. Obwohl Graphen aufgrund seiner hervorragenden mechanischen Eigenschaften bei den Forschern auf dem Gebiet der Nanotribologie großes Interesse auf sich gezogen hat [3, 7], sind die Reibungseigenschaften von Graphen, das auf der Goldoberfläche gleitet, nur unzureichend verstanden. Bisher konzentrieren sich viele tribologische Studien zu Graphen auf die Reibungskraft zwischen Graphen und einer Abtastsondenspitze [8,9,10,11,12,13,14]. Beispielsweise ergaben die Experimente der Rasterkraftmikroskopie (AFM) zur Reibung an chemisch modifiziertem Graphit einen negativen Reibungskoeffizienten [9]. Die Experimente mit dem Reibungskraftmikroskop (FFM) von Graphen mit wenigen Schichten ergaben, dass die Reibung mit abnehmender Anzahl der Graphenschichten zunahm [10, 11]. Diese Phänomene werden durch den Faltenbildungseffekt von Graphen erklärt [9,10,11]. Es wird vermutet, dass die Reibung zwischen einer Graphen-Flake und Graphit gemessen wurde, da die Spitze beim Gleiten auf Graphit eine Flocke mitzog [8, 14]. Es wurde festgestellt, dass die Rotationsbewegung, die mit der seitlichen Bewegung der Flocken für lamellare Feststoffe gekoppelt ist, zu einer Reibungserhöhung aufgrund der Neuorientierung der Flocken in eine entsprechende Konfiguration führt [15]. Gleichzeitig haben sich einige Wissenschaftler auch der Untersuchung der Reibung von Graphen und/oder Gold mit anderen Techniken gewidmet. Die Quarzkristall-Mikrowaage (QCM) wurde verwendet, um die Gleitfähigkeit von Gold auf Graphen [16] und die Gleitreibung eines festen Xenonfilms auf einem Graphen/Ni(111)-Substrat [17] zu untersuchen. Sowohl QCM-Experimente als auch Molekulardynamik(MD)-Simulationen zeigen, dass die Reibung einer inkommensuralen Kr-Monoschicht auf Au einem viskosen Reibungsgesetz folgt [18, 19]. MD-Simulationen werden durchgeführt, um die Haftreibung von zweidimensionalen Goldinseln und dreidimensionalen Goldclustern auf Graphitsubstrat zu untersuchen [20]. Es hat sich herausgestellt, dass die Gleiterdicke aufgrund der höheren effektiven Steifigkeit dicker Cluster die Schmierfähigkeit fördern kann. Die größenabhängige Grenzflächenkommensurabilität wurde auch durch MD-Simulationen von Xenonatomen auf Graphen- und Au-Substrat [21] aufgedeckt, die mit den Simulationen von Krypton- und Siliziumclustern auf Cu-Substrat [22] übereinstimmen, was die Größenabhängigkeit der Haftreibung erklären kann. Vor kurzem wurde die Superschmierfähigkeit von Graphen-Nanobändern auf einem Au(111)-Substrat bei niedriger Temperatur beobachtet [23]. Kitt et al. maß direkt die Reibung von Graphen, das über ein SiO₂ . gleitet Substrat und fanden heraus, dass das Reibungsverhalten von Monolayer- und Bilayer-Graphen gegen das Amontons-Gesetz verstößt [24]. Insgesamt ist zu erwarten, dass Graphen als reines zweidimensionales Material ein atypisches Reibungsverhalten für ein Graphen-Substrat-System zeigt. Leider fehlt noch eine detaillierte Untersuchung der Gleitreibung von Graphen über einem Goldsubstrat, obwohl die Grenzflächeneigenschaften zwischen Graphen und Metallen systematisch untersucht wurden [25,26,27,28].

Um diese Lücke zu schließen, wird in diesem Artikel das Gleitreibungsverhalten mobiler Graphenflocken über einem einkristallinen Goldsubstrat gründlich mit Molekulardynamiksimulationen (MD) untersucht. Wir untersuchen die Auswirkungen der Flockengröße, Flockenform, des relativen Rotationswinkels zwischen Flocken und Substrat und der Kristallorientierung des Substrats, um die Reibungseigenschaften zu klären.

Methoden

Simulationsmethode

Um ein AFM-Experiment zu simulieren, bei dem eine Graphenflocke, die durch eine Feder an einer Spitze befestigt ist, über ein Goldsubstrat gleitet [29], erstellen wir ein MD-Modell, das aus einer Graphenflocke aus N . besteht Atome und ein einkristallines Goldsubstrat, siehe Abb. 1. Die drei Atomschichten am Boden des Substrats werden im Raum fixiert gehalten, um als Grenzatome zu dienen. Um die Temperatur des Systems zu steuern, werden vier Atomschichten benachbart zu den Grenzatomen im Substrat als Thermostatatome gewählt. Die Thermostatatome werden durch die Geschwindigkeitsskalierungsmethode [30] auf einer konstanten Temperatur von 300 K gehalten. In dieser Arbeit betrachten wir erstens nicht die Rotation von Graphen während des Gleitens; die Atome im Graphen dürfen sich nur im x . bewegen und z Richtungen, sind aber in den y Richtung, was die Simulationen vereinfacht. Dies ist der Schwerpunkt dieser Arbeit. Dann führen wir weiter einige MD-Simulationen ohne die Bewegungseinschränkung von Graphen im y . durch Richtung, um den realen Versuchsbedingungen besser zu entsprechen. Die Flockenatome werden von einem virtuellen Atom mit konstanter Geschwindigkeit durch eine harmonische Feder gezogen. Die Feder parallel zur Substratoberfläche hat eine Seitensteifigkeit von 10 N/m und wird verwendet, um die Verformung des Kragträgers und des Spitzenscheitels eines AFM-Systems darzustellen [31]. In den Simulationen wird eine konstante Normallast direkt auf die Flockenatome aufgebracht [29, 31]. Die Graphenflocke wird von einem virtuellen Atom mit einer konstanten Geschwindigkeit von 10 m/s seitlich gezogen. Die Bewegungsgleichungen werden mit einem Geschwindigkeits-Verlet-Algorithmus integriert. Der Zeitschritt beträgt 1 fs. Grenzen sind im x . periodisch und y Wegbeschreibung, kostenlos im z Richtung.

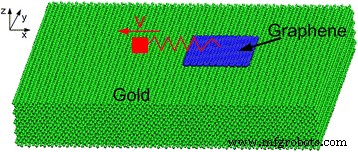
Simulationsmodell des Reibungsprozesses

Um den Effekt der Kristallorientierung des Substrats zu untersuchen, führen wir MD-Simulationen der Gleitreibung auf drei verschiedenen Oberflächen von Au(111), (001) bzw. (110)-Ebenen durch. Für Au(111)-Oberflächen werden die Koordinatensysteme als \( x-\left[11\overline{2}\right]\), \( y-\left[1\overline{1}0\right]\ )_, und z -[111] und die Größe beträgt 19,98  × 15,0  ×  3,06 nm ³ . Für die Au(001)-Oberfläche werden die Koordinatensysteme als x . angenommen -[100], y -[010] und z- [001] und die Größe des Substrats beträgt 19,99   ×  15,1  ×  3,06 nm ³ . . Für die Au(110)-Oberfläche werden die Koordinatensysteme als x . angenommen -[001], \( y-\left[1\overline{1}0\right] \)_, und z -[110] und die Größe beträgt 19,99  × 15,0  × 3,03 nm ³ . Die Gitterabstände entlang der Gleitrichtung für Au(111), Au(110) und Au(001)-Oberflächen betragen 9,99 Å, 4,08  bzw. 4,08 . Wenn nicht angegeben, wird Au(111) als Substrat verwendet. In den Simulationen werden mehrere unterschiedliche Flockengrößen und -formen modelliert. Die Standardflockenform ist ein Quadrat mit einer Größe von 5,8 nm (Anzahl der Atome N = 1344). Das x -Achse entlang der Sesselrichtung des Graphens und der y -Achse verläuft in Zickzack-Richtung, mit dem z -Achse senkrecht zum Graphen.

Die interatomaren Kräfte innerhalb von Au werden aus einem Potential der eingebetteten Atommethode (EAM) abgeleitet [32]. Das EAM-Potential war sehr erfolgreich bei der Modellierung der elastischen Eigenschaften, der Defektbildungsenergien und der Bruchmechanismen verschiedener Metalle [32, 33]. Es wurde auch erfolgreich angewendet, um die Oberflächeneigenschaften von Metallen wie Oberflächenenergien und Oberflächenrekonstruktionen zu beschreiben [32,33,34]. Das weit verbreitete AIREBO-Potential wird verwendet, um die Wechselwirkung von Atomen innerhalb von Graphen zu beschreiben [35]. Die Wechselwirkung zwischen Graphen und Au-Substrat wird durch das Standard-Lennard-Jones (LJ)-Potential modelliert, das verwendet wurde, um viele Nichtgleichgewichtsphänomene wie Reibung und Diffusion von Goldclustern auf Graphit zu untersuchen [36, 37]. Die LJ-Parameter [28, 29] sind:ε = 22,0 meV und σ = 2,74 Å. Die MD-Simulationen werden mit dem großskaligen atomaren/molekularen massiv parallelen Simulator (LAMMPS) durchgeführt [38]. In den Simulationen wird die Graphen-Flake zunächst über der Au-Substratoberfläche positioniert. Nachdem das Reibungssystem vollständig entspannt ist, beginnt das virtuelle Atom entlang des negativen x . zu gleiten Richtung mit konstanter Geschwindigkeit.

Ergebnisse und Diskussionen

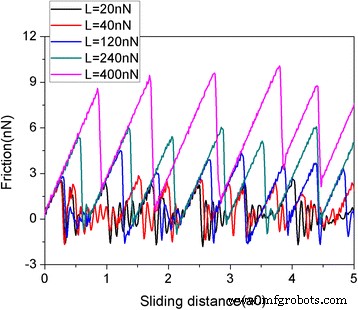
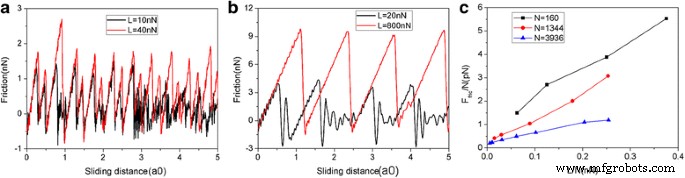
Abbildung 2 zeigt die Reibungskraft als Funktion der Gleitstrecke bei verschiedenen Normallasten. In diesem Papier ist die Gleitstrecke die des virtuellen Atoms. Die Reibungskraft wird durch die Verformung der Feder wie in einem AFM-Experiment gemessen. Die Graphen-Flake hat eine quadratische Form mit einer Größe von 5,8 nm und besteht aus 1344 Atomen. Es ist klar, dass die Reibungskräfte kontinuierlich ansteigen, gefolgt von starken Abfallen, die typisch für Stick-Slip-Bewegungen sind. Der abrupte Abfall der Reibungskraft führt zu einer Energiedissipation und impliziert das Auftreten von Übergängen zwischen mehreren metastabilen Zuständen mit lokalen potentiellen Energieminima [39]. Es ist vernünftig, dass die Reibungskraft mit der Last L zunimmt. Um den Größeneffekt zu untersuchen, werden zwei weitere quadratische Flocken mit Größen von 2,0 nm (N = 160 Atome) und 10,0 nm (N = 3936 Atome) angenommen. Die Variation der Reibungskraft und der durchschnittlichen Reibungskraft für verschiedene Flockengrößen während des Gleitprozesses sind in Abb. 3 dargestellt. Wie bei der 5,8-nm-Flake kann auch eine deutliche Stick-Slip-Reibung sowohl für die 2,0- als auch für die 10- nm Flocken. Darüber hinaus existiert eindeutig ein Größeneffekt bei der durchschnittlichen Reibungskraft pro Atom F _fries /N, siehe Abb. 3c. Bei gleicher Belastung betragen die durchschnittlichen Reibungskräfte pro Atom F _fries /N sind größer für eine kleinere Flocke. Dieser Größeneffekt resultiert aus der mit zunehmender Flockengröße fortschreitend abnehmenden Rolle der Kanten bei der Reibung [40, 41]. Es sollte beachtet werden, dass sowohl die QCM-Experimente als auch die MD-Simulationen ergaben, dass die Reibung von Adsorbatclustern mit zunehmender Größe abnimmt [18,19,20,21,22], in Übereinstimmung mit unseren Simulationen. Die Größenabhängigkeit der Reibung in den QCM-Experimenten und MD-Simulationen wird jedoch durch die größenabhängige Grenzflächenkommensurabilität erklärt [18,19,20,21,22].

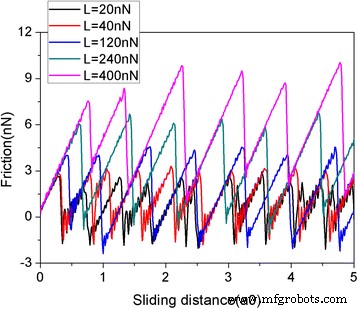
Reibungskraft als Funktion der Gleitstrecke bei verschiedenen Normallasten (L). Die Flocke hat eine quadratische Form mit einer Größe von 5,8 nm. Hier ist a0 (= 9,99 Å) der Gitterabstand von Au(111) entlang der Gleitrichtung

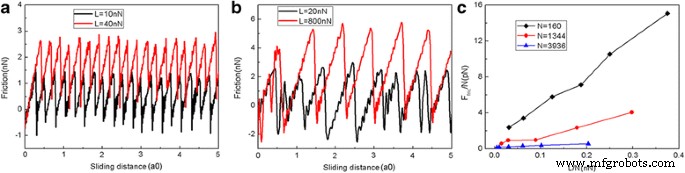
Die Variation der Reibungskraft und der durchschnittlichen Reibungskraft für verschiedene Flockengrößen. Die typische Reibungskraft als Funktion der Gleitstrecke für 2,0 nm (N = 160 Atome) Flocken (a ) und 10 nm (N = 3936 Atome) Flocke (b ). c Die durchschnittliche Reibungskraft pro Atom (F _fries /N) als Funktion der Belastung pro Atom (L/N). Hier ist a0 (= 9,99 Å) der Gitterabstand von Au(111) entlang der Gleitrichtung

Da die Form des Schiebers eine bedeutende Rolle bei der Bestimmung der Reibung spielt [42, 43], modellieren wir zur weiteren Untersuchung des Einflusses der Flockenform auf den Reibungsprozess den Gleitreibungsprozess auch unter Verwendung einer runden Graphenflocke (N = 1080 Atome) und eine dreieckige Graphen-Flake (N = 654 Atome). Abbildung 4 zeigt den Verlauf der typischen Reibungskräfte und der durchschnittlichen Reibungskräfte für verschiedene Flockenformen während des Gleitvorgangs. Wie in Abb. 4a, b gezeigt, bei kleinen Lasten (L = 20 nN für runde Flocken und L = 10 nN für dreieckige Flocken), schwankt die Reibungskraft kontinuierlich um Null und es kann eine extrem niedrige Reibung (Superschmierfähigkeit) beobachtet werden. Bei großen Normallasten (L = 400 nN für runde Flocken und L = 200 nN für dreieckige Flocken), zeigt die Flocke eine deutliche Stick-Slip-Bewegung und eine große Reibungskraft [39]. Bei gleicher Belastung betragen die durchschnittlichen Reibungskräfte pro Atom F _fries /N sind die größten für die quadratischen Flocken und die kleinsten für die dreieckigen Flocken, während F _fries /N für die runde Flocke liegen dazwischen. Außerdem ist die Differenz der durchschnittlichen Reibungskräfte pro Atom F _fries /N zwischen runder und dreieckiger Flocke ist eher klein. Aber F _fries /N für die quadratische Flocke ist viel größer. Daher ist klar, dass die Flockenform beim Gleitprozess eine entscheidende Rolle spielt.

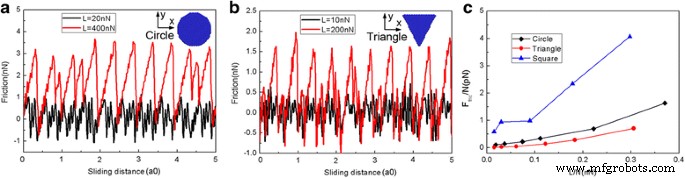
Die Variation der Reibungskraft und der durchschnittlichen Reibungskraft für verschiedene Flockenformen. Die typische Reibungskraft als Funktion der Gleitstrecke für die Runde (N = 1080 Atome) Flocke (a ) und dreieckig (N = 654 Atome) Flocke (b ). c Die durchschnittliche Reibungskraft pro Atom (F _fries /N) als Funktion der Belastung pro Atom (L/N). Hier ist a0 (= 9,99 Å) der Gitterabstand von Au(111) entlang der Gleitrichtung

Es ist bekannt, dass auch die Orientierung der Flocken relativ zum Substrat entscheidend für die Bestimmung der Reibung ist [42]. Um den Orientierungseffekt auf die Reibung zu untersuchen, wird die Graphenflocke um verschiedene Winkel um das z . gegen den Uhrzeigersinn gedreht -Achse senkrecht zum Kontakt. Der Drehwinkel 0° (ohne Drehung) entspricht der Situation, bei der x -Achse entlang der Sesselrichtung des Graphens, während der Drehwinkel 90° der Situation entspricht, in der das x -Achse ist in Zickzack-Richtung. Die Variation der Reibungskraft als Funktion der Gleitstrecke für die 5,8-nm-Quadratflocke mit unterschiedlichen Drehwinkeln bei L = 240 nN ist in Abb. 5 dargestellt. Die entsprechenden durchschnittlichen Reibungskräfte F _fries für verschiedene Drehwinkel bei unterschiedlichen Normalbelastungen werden wie in Abb. 6 dargestellt berechnet. Es ist offensichtlich, dass für Flocken mit θ = 15° und θ = 45° die Reibungskräfte kontinuierlich um Null schwanken und Superschmierung beobachtet werden kann, vgl. 5b, d. Darüber hinaus ist bei den durchschnittlichen Reibungskräften für Flocken mit θ = 15° und θ = 45° ein geringer Unterschied zu beobachten, siehe Abb. 6. Für die Flocken mit θ = 30°, 60° und θ = 90° ist die Flocken zeigen eine offensichtliche Stick-Slip-Bewegung und eine relativ große Reibungskraft. Außerdem ist die durchschnittliche Reibungskraft für einen größeren Drehwinkel der Flocken mit = 30°, 60° und θ = 90° größer. Die Reibungskräfte für Flocken mit Rotation sind alle viel kleiner als für die Flocken ohne Drehung (θ = 0°).

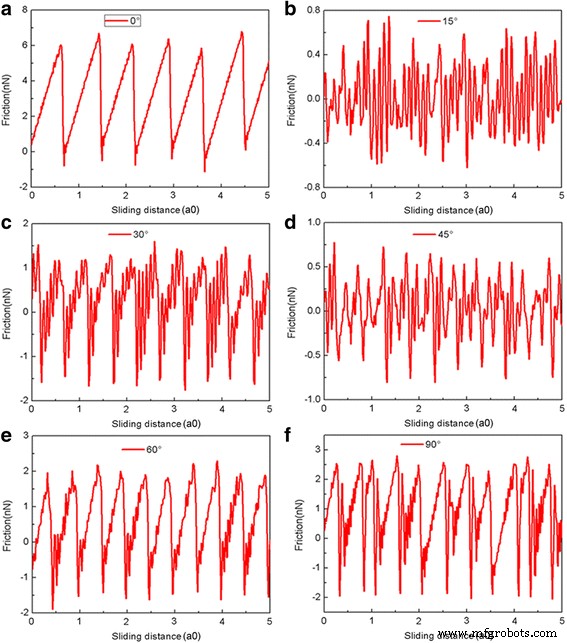
Die Reibungskraft im Vergleich zum Gleitweg der 5,8 nm großen quadratischen Flocke bei L = 240 nN für verschiedene Drehwinkel (θ = 0°, 15°, 30°, 45°, 60°, 90°). a –f entsprechen jeweils dem Drehwinkel 0°~90°. Hier ist a0 (= 9,99 Å) der Gitterabstand von Au(111) entlang der Gleitrichtung

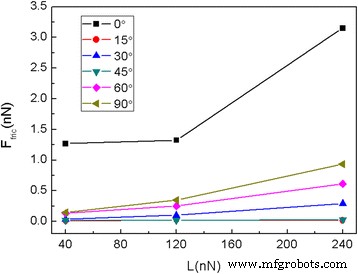
Die durchschnittliche Reibungskraft Ffric der 5,8-nm-Quadratlamelle für verschiedene Drehwinkel bei verschiedenen Normalbelastungen

Die Tatsache, dass einkristallines Gold signifikante anisotrope Effekte zeigt, ermutigt uns, den Einfluss der Kristallorientierung des Substrats auf den Reibungsprozess weiter zu untersuchen. Wir führten MD-Simulationen für zwei weitere Kombinationen von Kristallorientierung und Gleitrichtung durch, d. h. (001) [100] und (110) [001]. Die Reibungskraft und die durchschnittliche Reibungskraft F _fries der 5,8-nm-Quadratflocken, die auf den Au-Substraten mit unterschiedlicher Kristallorientierung gleiten, sind in den Fign. 7 und 8 bzw. Erwartungsgemäß steigt die Reibungskraft mit der normalen Belastung. Es ist ersichtlich, dass bei gleicher Belastung die Reibungskräfte für die Au(001)- und Au(110)-Oberflächen größer sind als die für die Au(111)-Oberfläche und die Reibungskräfte für die Au(110)-Oberfläche sind am größten.

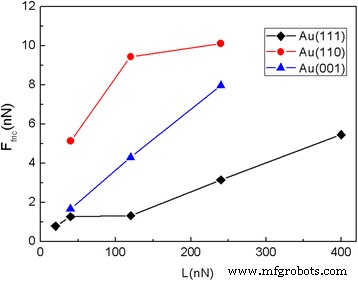
Die Reibungskraft der 5,8-nm-Quadratflocken, die auf dem (a ) Au(001) und (b ) Au(110)-Oberflächen als Funktion der Gleitstrecke bei verschiedenen Normallasten. Hier ist a1 (= 4,08 Å) der Gitterabstand von Au(001) entlang der Gleitrichtung und a2 (= 4,08 Å) ist der Gitterabstand von Au(110) entlang der Gleitrichtung

Die durchschnittliche Reibungskraft F _fries der 5,8-nm-Quadrat-Flake, die auf den Au-Substraten mit unterschiedlicher Kristallorientierung bei unterschiedlichen Normallasten gleitet

Nach dem bekannten Prandtl-Tomlinson-Modell [44] steht die Reibungskraft in engem Zusammenhang mit der Grenzflächenenergiewellung [45,46,47]. Um die zugrunde liegenden Mechanismen hinter dem signifikanten anisotropen Effekt der Reibung zu untersuchen, berechneten wir die potentielle Wechselwirkungsenergie zwischen der Flocke und dem Au-Substrat, wenn wir die Flockenposition änderten [46]. Die potentielle Energie wird für eine starre Flocke in einer festen Höhe berechnet, die der durchschnittlichen Höhe für die gegebene Last entspricht [29]. Drei typische Konturdiagramme, die die räumliche Variation der potentiellen Energie für Au(111), Au(110) und Au(001)-Oberflächen bei L . darstellen = 120 nN sind jeweils in den Fig. 9a–c gezeigt. Um die Potenzialenergieflächen-(PES-)Karten in Abb. 9 zu erhalten, verwenden wir 21 Netzpunkte entlang der beiden x und y Richtungen. In Abb. 9 betragen die berechneten Energiekorrugationen für Au(111), Au(110) und Au(001) 3,5 eV, 66,6 eV bzw. 29,1 eV. In Abb. 9a–c ist eine schwarze durchgezogene Linie (y = 0) auf den PES-Karten wird verwendet, um den Gleitpfad der Flocke anzuzeigen. Die potentielle Graphen-Gold-Wechselwirkungsenergie entlang des Gleitpfads für Au(111), Au(110) und Au(001) ist ebenfalls in Abb. 9d–f dargestellt. Die Energiewelligkeiten entlang des Gleitpfads für Au(111), Au(110) und Au(001) in Abb. 9 betragen 3,5 eV, 59,7 eV bzw. 29,1 eV. Es ist deutlich zu erkennen, dass die Amplitude der Energiewellung den gleichen anisotropen Effekt wie die Reibung zeigt. Die Energiekorrugation für die Au(001)- und Au(110)-Oberfläche ist größer als die für die Au(111)-Oberfläche, und die Energiekorrugation für die Au(110)-Oberfläche ist am größten. Dies erklärt daher eindeutig den signifikanten anisotropen Effekt der Reibung während des Gleitprozesses [45,46,47]. Der Befund, dass die Reibungskraft mit abnehmender Graphen-Substrat-Wechselwirkungsstärke (Energiekorrugation) abnimmt, stimmt mit den MD-Simulationen [16] und dem QCM-Experiment [17] überein.

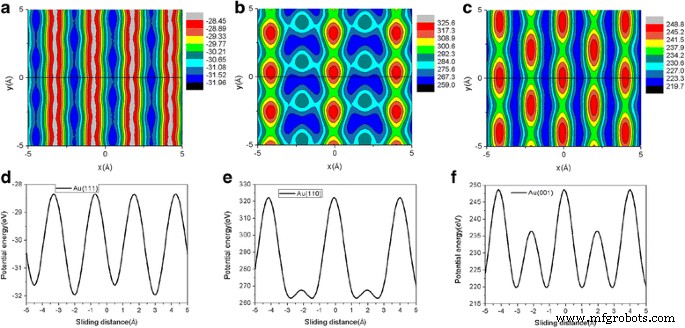
Konturkarten der potentiellen Energie für die Au(111), Au(110) und Au(001)-Oberfläche bei L = 120 nN werden in a angezeigt –c , bzw. Die 5,8-nm-Quadrat-Graphen-Flake wird verwendet. In a –c , eine schwarze durchgehende Linie (y = 0) auf den Karten wird verwendet, um den Gleitweg der Flocke anzuzeigen. Die potentielle Graphen-Gold-Wechselwirkungsenergie entlang der Gleitbahn für die Au(111), Au(110) und Au(001)-Oberfläche ist auch in d . aufgetragen –f , bzw. Die Einheit der potentiellen Energie ist eV. Die durchschnittliche Höhe der Flocke bei L = 120 nN für die Au(111), Au(110) und Au(001)-Oberfläche beträgt 2,36 Å, 2,1 Å bzw. 2,17 Å

Um den realen experimentellen Bedingungen besser zu entsprechen, haben wir außerdem MD-Simulationen der Gleitreibung ohne die Bewegungseinschränkung von Graphen im y . durchgeführt Richtung, in diesem Fall kann sich die Flocke drehen und im y bewegen Richtung. Abbildung 10 zeigt die Reibungskraft als Funktion der Gleitstrecke bei verschiedenen Normallasten für die Graphen-Flake mit einer quadratischen Form und einer Größe von 5,8 nm bestehend aus 1344 Atomen. Obwohl sich die Werte der Reibungskraft geändert haben, ist ersichtlich, dass die Reibungskräfte kontinuierlich ansteigen, gefolgt von abrupten Abfallen, was eine offensichtliche Stick-Slip-Bewegung ähnlich wie in Abb. 2 darstellt. Die Reibungskraft steigt erwartungsgemäß mit der Last an. Wir haben auch den Reibungsprozess von zwei weiteren quadratischen Graphenflocken mit einer Größe von 2,0 nm (N = 160 Atome) und 10,0 nm (N = 3936 Atome) ohne die Bewegungsbeschränkung von Graphen im y Richtung. Die Variation der Reibungskraft und der durchschnittlichen Reibungskraft für verschiedene Flockengrößen während des Gleitprozesses sind in Abb. 11 dargestellt. Ähnlich wie in Abb. 3 beobachten wir auch eine offensichtliche Stick-Slip-Reibung sowohl für die 2,0- als auch für die 10-nm-Flakes. Darüber hinaus gibt es einen Größeneffekt bei der durchschnittlichen Reibungskraft pro Atom F _fries /N, siehe Abb. 11c. Bei gleichen Belastungen betragen die durchschnittlichen Reibungskräfte pro Atom F _fries /N sind für kleinere Flocken größer, was typisch für den Größeneffekt der Reibung ist. Insgesamt stellten wir fest, dass die wichtigsten Ergebnisse der MD-Simulationen des Reibungsprozesses mit y -Richtungsbewegung der Flake-Beschränkung bleibt bestehen, nachdem die Bewegungsbeschränkung der Graphen-Flake im y . gelockert wurde Richtung beim Gleiten.

Reibungskraft als Funktion der Gleitstrecke bei verschiedenen Normallasten (L ) für den Reibungsprozess ohne die Bewegungseinschränkung von Graphen im y Richtung. Die Flocke hat eine quadratische Form mit einer Größe von 5,8 nm. Hier ist a0 (= 9,99 Å) der Gitterabstand von Au(111) entlang der Gleitrichtung

Die Variation der Reibungskraft und der durchschnittlichen Reibungskraft für verschiedene Flockengrößen für den Reibungsprozess ohne die Bewegungseinschränkung von Graphen im y Richtung. Die typische Reibungskraft als Funktion der Gleitstrecke für 2,0 nm (N = 160 Atome) Flocken (a ) und 10 nm (N = 3936 Atome) Flocke (b ). c Die durchschnittliche Reibungskraft pro Atom (F _fries /N) als Funktion der Belastung pro Atom (L/N). Hier ist a0 (= 9,99 Å) der Gitterabstand von Au(111) entlang der Gleitrichtung

Schlussfolgerungen

In dieser Arbeit werden Molekulardynamiksimulationen eingesetzt, um das Gleitreibungsverhalten mobiler Graphenflocken über einem einkristallinen Goldsubstrat zu untersuchen. Die Auswirkungen der Flockengröße, Flockenform, des relativen Rotationswinkels und der Kristallorientierung des Substrats werden gründlich untersucht. Es wurde festgestellt, dass es einen Größeneffekt im Reibungsverhalten gibt. Bei gleicher Belastung betragen die durchschnittlichen Reibungskräfte pro Atom F _fries /N sind größer für eine kleinere Graphen-Flocke. Es zeigt sich auch, dass die Flockenform beim Reibungsprozess eine bedeutende Rolle spielt. Die durchschnittlichen Reibungskräfte pro Atom F _fries /N für die quadratischen Flocken sind viel größer als die für die dreieckigen und runden Flocken. Außerdem sind die durchschnittlichen Reibungskräfte pro Atom F _fries /N für die dreieckige Flocke sind die kleinsten. Wir fanden auch, dass der Einfluss der Orientierung von Graphenflocken relativ zum Au-Substrat entscheidend für die Bestimmung der Reibung ist. Die Reibungskräfte für die Graphen-Flake, die entlang der Sesselrichtung gleitet, sind viel größer als die für die Flocken bei Rotation. Die sehr geringen Reibungskräfte sind für Flakes mit θ = 15° und θ = 45° zu beobachten. Außerdem ist die Reibungskraft für einen größeren Drehwinkel der Flakes mit = 30°, 60° und θ = 90° größer. Außerdem zeigt sich, dass die Reibung einen deutlichen anisotropen Effekt zeigt. Die Reibungskräfte für die Au(001)- und Au(110)-Oberflächen sind größer als die für die Au(111)-Oberfläche, und die Reibungskräfte für die Au(110)-Oberfläche sind am größten. Dieser anisotrope Reibungseffekt wird dem anisotropen Effekt der potentiellen Energiewellung zugeschrieben. Diese Ergebnisse liefern nicht nur Einblicke in die zugrunde liegenden Mechanismen des Gleitens von Graphenflocken auf einem Goldsubstrat, sondern können auch den Entwurf und die Herstellung von nanoskaligen graphenbasierten Geräten leiten.