Kontrollierbare optische Bistabilität und Vier-Wellen-Mischung in einer photonischen Molekül-Optomechanik

Hintergrund

Optomechanische Systeme (OMS) [1], bestehend aus optischen Hohlräumen, die mit mechanischen Resonatoren gekoppelt sind und die strahlungsdruckinduzierte kohärente Photonen-Phonon-Wechselwirkungen untersuchen, haben in letzter Zeit viel Aufmerksamkeit auf sich gezogen, weil sie eine Plattform bieten, um mechanische Resonatoren und elektromagnetische Felder zu manipulieren und die Weg für potenzielle Anwendungen optomechanischer Geräte, wie Phononenlaser [2, 3], Sensorik [4], Phononenquetschung [5], Realisierung von Quetschlicht [6–8], Grundzustandskühlung [9–11], und optomechanisch induzierte Transparenz (OMIT) [12–15] induziertes Speicherlicht in Festkörperbauelementen [16, 17]. Obwohl dem einzelnen OMS die meiste Aufmerksamkeit gewidmet wurde, ist es möglich, zusammengesetzte OMS durch die Integration mehrerer optischer oder mechanischer Moden zu realisieren, wie z , 21] werden zu einer Tendenz, die OMS und ihre potenziellen Anwendungen in der Quanteninformationsverarbeitung weiter zu untersuchen. Basierend auf der Hybridverbindung OMS wurden die Übertragung eines Quantenzustands [22], die OMIT-ähnliche Phononenkühlung [23], der optomechanische Dunkelmodus [24] und die phononenvermittelte elektromagnetisch induzierte Absorption [25] umfassend erforscht. In den zahlreichen zusammengesetzten OMS haben als natürliche Erweiterung des generischen OMS zwei direkt gekoppelte Mikrokavitäten im Flüstergaleriemodus (WGM), die als photonische Moleküle bezeichnet werden [26, 27] mit optomechanischem Effekt in einer WGM-Mikrokavität viel Aufmerksamkeit auf sich gezogen. Es gibt zwei Arten von Wechselwirkung in dem optomechanischen Verbundsystem aus Photonen-Molekülen:Die erste ist die durch den Strahlungsdruck induzierte optomechanische Wechselwirkung und die andere ist die Hohlraum-Kavitäten-Kopplung über abstimmbares Photonentunneln. Die beiden Wechselwirkungen zusammen führen zu mehreren interessanten Phänomenen, darunter Phononen-Lasern [2, 3], Chaos [28], Grundzustandskühlung [23] und kohärente Kontrolle der Lichtübertragung [25, 29, 30].

Andererseits bietet OMS auch eine Plattform, um den nichtlinearen Effekt der Licht-Materie-Wechselwirkung zu untersuchen. Unter all den nichtlinearen Phänomenen in OMS sind optische Bistabilität und Vierwellenmischung (FWM) typische nichtlineare optische Phänomene, die im Fokus der Forscher stehen. In den letzten Jahren wurde das bistabile Verhalten der mittleren Photonenzahl in der Kavität ausführlich in verschiedenen OMS untersucht, wie z. 35] und andere hybride OMS [36, 37]. Darüber hinaus kann FWM als die Kavität beschrieben werden, die von einem starken Pumplaser mit der Frequenz ω . angetrieben wird _p und eine schwache Sondenlaserfrequenz ω _s , und dann würden sich zwei Pumpphotonen mit einem Sondenphoton über den mechanischen Modus mischen, um ein Idlerphoton bei der Frequenz 2ω . zu ergeben _p −ω _s in OMS, und es wird auch in früheren Arbeiten untersucht, wie zum Beispiel die Modenteilung in einem optomechanischen System mit starker Kopplung [38], ein kohärentes mechanisches Antriebs-OMS [39, 40] und ein optomechanisches Zweimoden-Cavity-System [41]. Optische Bistabilität und FWM wurden jedoch selten in Komposit-OMS mit photonischen Molekülen untersucht, bei denen die Kopplungsstärke durch J . dargestellt wird der beiden Kavitäten spielen eine Schlüsselrolle bei diesen nichtlinearen optischen Phänomenen.

In der vorliegenden Arbeit betrachten wir ein optomechanisches Verbundsystem mit photonischen Molekülkavitäten, das aus zwei WGM-Mikrokavitäten besteht, wobei eine WGM-Kavität eine optomechanische Kavität mit hoher Kavitätendissipation ist κ , und die andere WGM-Kavität ist eine gewöhnliche optische Hilfskavität mit hohem Qualitätsfaktor (Q) [42]. Wie Liu et al. [43] demonstriert, bleibt es schwierig, für denselben Resonatortyp gleichzeitig einen hohen Q-Faktor und ein kleines Modenvolumen (V) zu erreichen. In der Photonik-Molekül-Optomechanik durch Kopplung des ursprünglich optomechanischen Hohlraums c mit hoher Kavitätenableitung κ (ohne hohes Q) in einen Hilfshohlraummodus a mit hohem Q, aber großem V kann die Forderung nach hohem Q und kleinem V für dieselbe Kavität entfallen. Wir führen einen Verhältnisparameter δ . ein =κ _c /κ _a , wobei κ _c =ω _c /Q _c und κ _a =ω _a /Q _a sind die Zerfallsraten der Hohlraummoden c und a (ω _c und ω _a sind die Frequenzen der Kavität c und a ), um den nichtlinearen Effekt in der Optomechanik photonischer Moleküle zu untersuchen. Hier der optomechanische Hohlraum c wird vom Pumplaser angetrieben, während die Hilfskavität a wird vom Sondenlaser angesteuert. Der Hohlraum c ist an Hohlraum a . gekoppelt über evaneszentes Feld und die Kopplungsstärke J zwischen den beiden Kavitäten kann durch Variation des Abstands zwischen den beiden WGM-Kavitäten gesteuert werden [26]. Wir untersuchen die optische Bistabilität und FWM basierend auf dem zusammengesetzten photonischen Molekül OMS durch Variation der Kopplungsstärke J zwischen den Hohlraumresonatoren, und eine abstimmbare und steuerbare optische Bistabilität und FWM kann durch Manipulation der Kopplungsstärke J . erreicht werden zwischen den beiden Hohlräumen. Außerdem mit Anpassung des Parameters δ und die Pumpleistung P , kann der FWM-Prozess gesteuert werden.

Modell und Theorie

Die Optomechanik photonischer Moleküle ist in Abb. 1 dargestellt. Die erste Kavität unterstützt eine optische Mode c mit der Frequenz ω _c angetrieben vom Pumplaser mit der Frequenz ω _p und die Amplitude \(\varepsilon_{p}=\sqrt{P/\hbar\omega_{p}}\). Der Strahlungsdruck induziert eine mechanische Mode b mit der mechanischen Resonatorfrequenz ω _m , und die optomechanische Einzelphotonen-Kopplungsrate beträgt g =g ₀ x ₀ (g ₀ =ω _c /R und R ist der Hohlraumradius c ), und die Nullpunktsschwankung der Position des mechanischen Oszillators ist \(x_{0}=\sqrt {\hbar/2M\omega_{m}}\) [13]. Dann ist der Hamiltonoperator der Optomechanik c ist [13]

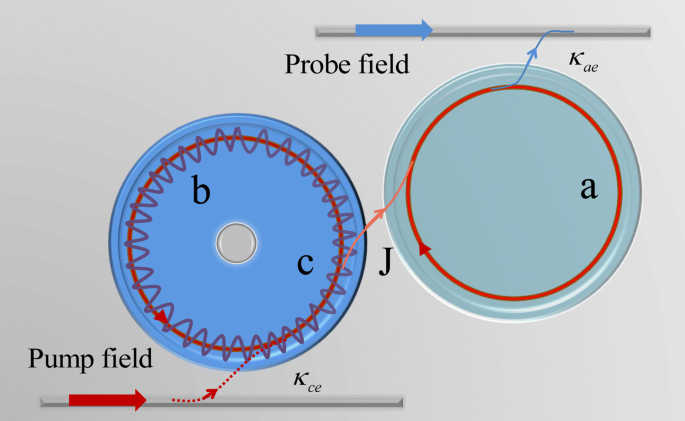
Schematische Darstellung des optomechanischen Verbundsystems mit Photonen-Molekül-Kavitäten einschließlich zweier WGM-Kavitäten. Die erste WGM-Kavität mit High-Cavity-Dissipation κ ist optomechanischer Hohlraum c angetrieben von einem Pumplaser, und die Strahlungsdruckkraft induziert den mechanischen Modus b Kopplung an Hohlraum c mit Kopplungsstärke g . Die zweite WGM-Kavität a ist eine Hilfskavität, die von einem Sondenlaser mit hohem Qualitätsfaktor (Q) angetrieben wird. Der optomechanische Hohlraum c ist an Hohlraum a . gekoppelt über ein evaneszentes Feld, und wir führen einen Parameter J . ein um die Kopplungsstärke der beiden Hohlräume zu beschreiben, die durch Variation des Abstands zwischen ihnen gesteuert werden kann [26]

wo Δ _c =ω _c −ω _p ist die Verstimmung von Pumpfeld und Kavität c . c und c ^† repräsentieren die bosonischen Vernichtungs- und Erzeugungsoperatoren des Hohlraummodus c , und b ^† (b ) ist der Erzeugungs-(Vernichtungs-)Operator des mechanischen Modus. Die Hilfskavität unterstützt nur einen optischen Modus a angetrieben vom Sondenlaser mit der Frequenz ω _s , und seine Amplitude ε _s ist \(\varepsilon_{s}=\sqrt{ P_{s}/\hbar\omega_{s}}\). Wir stellen die Vernichtungs- und Erzeugungsoperatoren a . vor und a ^† den Hohlraum beschreiben a , und sein Hamilton-Operator ist [13]

wo Δ _a =ω _a −ω _p ist die Verstimmung von Pumpfeld und Kavität a , und Ω =ω _s −ω _p ist die Pump-Probe-Verstimmung. Wir verwenden zwei sich verjüngende Fasern zur Anregung des Hohlraummodus a und Hohlraummodus c als Lichtwellenleiter mit der Koppelrate κ _ae und κ _ce . Der optomechanische Hohlraum c paart sich mit der Höhle a durch ein evaneszentes Feld und die Hohlraum-Kavität-Kopplungsrate J kann durch Änderung des Abstands zwischen ihnen effizient abgestimmt werden [26]. Wenn die Kopplungsstärke J zwischen den beiden Hohlräumen schwach ist, dann ist die Energie aus Hohlraum c kann nicht leicht in die Kavität übertragen werden a . Umgekehrt, wenn die Kopplungsstärke J nimmt mit abnehmendem Abstand zwischen den beiden Hohlräumen zu, dann kann die Energie leicht aus den beiden Hohlräumen fließen. Die linear gekoppelte Wechselwirkung zwischen den beiden Hohlräumen wird beschrieben durch [26] \(\hbar J\left (a^{\dag}c+ac^{\dag}\right)\). Dann ist der gesamte Hamilton-Operator im rotierenden Wellensystem der Pumpfrequenz ω _c kann geschrieben werden [3, 13, 23]

Die Zerfallsrate des Modus mit zwei Kavitäten κ =κ _c =κ _a =κ _ex +κ ₀ mit der intrinsischen Photonenverlustrate κ ₀ , und κ _ex beschreibt die Geschwindigkeit, mit der Energie den optischen Hohlraum in sich ausbreitende Felder verlässt [13]. Hier betrachten wir der Einfachheit halber nur die Bedingung von κ _ex =κ ₀ =κ _ae =κ _ce , und wir betrachten ω _c =ω _a .

Wir verwenden die Heisenberg-Bewegungsgleichung \(i\hbar\partial_{t}O=[O,H]\) (O =a ,c ,X ) und führen entsprechende Dämpfungs- und Rauschoperatoren ein, und wir erhalten die Quanten-Langevin-Gleichungen wie folgt [44]:

wobei X =b ^† +b ist der Positionsoperator und γ _m ist die Abklingrate des Resonators. a _in und c _in Beschreibung der Langevin-Geräusche folgen den Beziehungen [45]

Die Resonatormode wird durch den stochastischen Kraftprozess mit der folgenden Korrelationsfunktion beeinflusst [46]

wo k _B ist die Boltzmann-Konstante und T zeigt die Tanktemperatur an.

Wenn der optomechanische Hohlraum c von einem starken Pumplaser angetrieben wird, kann der Heisenberg-Operator in zwei Teile geteilt werden, d. h. stationärer Mittelwert O ₀ , und kleine Fluktuation δ O mit Null-Mittelwert 〈δ O =0. Die stationären Werte bestimmen die Photonenzahlen in der Kavität (n _a =|a _s | ² und n _c =|c _s | ² ) bestimmt durch

wobei \(\Updelta ^{^{\prime}}=\Updelta_{c}-2g^{2}n_{c}/\omega_{m}\). Diese Form gekoppelter Gleichungen ist charakteristisch für die optische Bistabilität. Im folgenden Abschnitt besprechen wir die Parameter wie die Pumpleistung P , die Hohlraum-Kavität-Kopplungsstärke J , und der Verhältnisparameter δ die die optische Bistabilität beeinflussen. Behalten Sie nur die linearen Terme der Fluktuationsoperatoren bei und machen Sie den Ansatz [47] 〈δ a 〉=a ₊ e ^{−i Ω t} +a ₋ e ^{ich Ω t} , δ c 〉=c ₊ e ^{−i Ω t} +c ₋ e ^{ich Ω t} , δ X 〉=X ₊ e ^{−i Ω t} +X ₋ e ^{ich Ω t} , erhalten wir dann

wobei \(\Lambda_{1}=igc_{s}^{2}\eta^{\ast}J^{2}\varepsilon_{s}\sqrt {\kappa_{ae}}\), Λ ₂ =(ich Δ _{a 2} +κ _a )(ich Δ ₂ +κ _c )[(ich Δ ₁ −κ _c )(ich Δ _{a 1} −κ _a )−J ² ], \(\Lambda_{3}=-g^{2}\eta^{\ast 2}n_{c}^{2}(i\Delta_{a1}-\kappa_{a})( i\Delta_{a2}+\kappa_{a})\), Δ _{a 1} =Δ _a −Ω , Δ _{a 2} =Δ _a +Ω , \(\Updelta_{1}=\Updelta ^{^{\prime}}-\Omega +g\eta n_{c}\), \(\Updelta_{2}=\Updelta ^{^{\ Primzahl }}+\Omega +g\eta^{\ast}n_{c}\), und \(\eta =2g\omega_{m}/(\omega_{m}^{2}-i\ gamma _{m}\Omega -\Omega^{2})\). Unter Verwendung der Standard-Input-Output-Beziehung [45] \(a_{\text {out}}(t)=a_{\text {in}}(t)-\sqrt {2\kappa_{a}}a(t )\), wobei a _aus (t ) ist der Ausgabefeldoperator und erhalten den Erwartungswert der Ausgabefelder:

wo a _aus (t ) ist der Ausgabefeldoperator. Gleichung (13) zeigt, dass das Ausgabefeld aus drei Termen besteht. Der erste Term entspricht dem Ausgangsfeld bei Fahrfeld mit Amplitude ε _p und Häufigkeit ω _p . Der zweite Term entspricht dem Sondenfeld mit der Frequenz ω _s im Zusammenhang mit dem Anti-Stokes-Feld, das zu OMIT führt, das in verschiedenen optomechanischen Systemen untersucht wurde [12–15, 48]. Das letzte entspricht dem Ausgabefeld mit der Frequenz 2 ω _p −ω _s bezogen auf das Stoke-Feld, das die FWM anzeigt. Beim FWM-Verfahren wechselwirken die beiden Photonen des Antriebsfeldes mit je einem Photon des Sondenfeldes mit den Frequenzen ω _p und ω _s geboren ein neues Photon der Frequenz 2 ω _p −ω _s . Die FWM-Intensität in Bezug auf das Sondenfeld kann definiert werden als [49]

die durch die optomechanische Kopplungsstärke g . bestimmt wird , die Pumpleistung P , die Hohlraum-Kavität-Kopplungsstärke J , und das Zerfallsratenverhältnis δ der beiden Kavitäten.

Numerische Ergebnisse und Diskussionen

In diesem Abschnitt untersuchen wir zunächst das bistabile Verhalten der stationären Photonenzahl n _c und n _a der beiden Kavitäten nach Gl. (10) und (11). Da es zu umständlich ist, den analytischen Ausdruck der Bistabilitätsbedingung anzugeben, werden hier die numerischen Ergebnisse präsentiert. Wir wählen die Parameter ähnlich denen in Ref. [13, 26] :die Parameter der Kavität c als [13]:g ₀ =12 GHz/nm, γ _m =41 kHz, ω _m =51,8 MHz, κ _c =5 MHz, m =20 ng, λ =750 nm und Q =1500, und die Größenordnung der Pumpleistung beträgt Milliwatt (1 mW =10 ⁻³ W). Für Hohlraum a , betrachten wir ω _a =ω _c und κ _c =κ _a . Die Kopplungsstärke J zwischen den beiden Resonatormoden spielt eine Schlüsselrolle und kann das bistabile Verhalten und die FWM beeinflussen. Es wurde experimentell berichtet, dass die Kopplungsstärke J hängt vom Abstand zwischen Kavität c . ab und Hohlraum a [26] (auch die Kopplungsstärke nimmt mit zunehmendem Abstand der beiden Hohlräume exponentiell ab). Hier erwarten wir die Kopplungsstärke \( J\sim \sqrt {\kappa_{c}\kappa_{a}}\).

Gleichungen (10) und (11) geben die Photonenzahlen der optomechanischen Kavität c . in der Kavität an und gewöhnlicher Hohlraum a sind gekoppelte kubische Gleichungen, die ein bistabiles Verhalten aufweisen. Wir betrachten zunächst die Bedingung von J =0, d. h. nur ein einziger optomechanischer Hohlraum c , und Abb. 2a zeigt die mittlere Photonenzahl in der Kavität n _c des optomechanischen Hohlraums c als Funktion der Hohlraumpumpenverstimmung Δ _c =ω _c −ω _p mit drei Pumpleistungen. Wenn die Pumpenleistung weniger als P beträgt =0,4 mW (wie P =0,1 mW) ist die Kurve nahezu lorentzsch. Mit zunehmender Leistung P auf einen kritischen Wert, die optomechanische Kavität c zeigt bistabiles Verhalten, wie in den Kurven für P . gezeigt =0,4 mW bis P =0,8 mW, wobei die anfängliche Lorentzsche Resonanzkurve asymmetrisch wird. Die mittlere Photonenzahl in der Kavität n _c hat drei reelle Wurzeln (Gl. (10)), und die größte und die kleinste Wurzel sind stabil und die mittlere ist instabil, was in Abb. 2a in einem Oval dargestellt ist. Betrachten wir jedoch den optischen Hohlraum a , d. h. J ≠0 wie J =1.0 κ _a , wird das bistabile Verhalten in gewisser Weise unterbrochen, wie in Fig. 2b gezeigt. Das liegt daran, dass beim optomechanischen Hohlraum c gekoppelt an optische Kavität a , Teile der Intrakavitätsphotonenzahl n _c des optomechanischen Hohlraums c wird in den optischen Hohlraum a . eingekoppelt , und daher die Intrakavitäts-Photonenzahl n _c sinkt und führt dann zu einem zerstörten bistabilen Verhalten. Abbildung 2c zeigt die mittlere Photonenzahl in der Kavität n _c des optomechanischen Hohlraums c als Funktion der Hohlraum-Kavität-Kopplungsstärke J mit drei Pumpleistungen. Offensichtlich ist die mittlere Photonenzahl in der Kavität n _c abhängig von der Pumpenleistung P , und die Intrakavitäts-Photonenzahl n _c nimmt mit zunehmender Kopplungsstärke immer ab J weil Teile der Photonenzahl in den optischen Hohlraum a . eingekoppelt werden . Darüber hinaus ist eine größere Verstimmung der Hohlraumpumpe von Vorteil, um das optisch bistabile Verhalten mit zunehmender Pumpleistung P . zu beobachten . Abbildung 2d zeigt die mittlere Photonenzahl in der Kavität n _c gegen die Pumpleistung P mit Hohlraum a an roten Seitenbändern (Δ _a =ω _m ) und blaue Seitenbänder (Δ _a =−ω _m ) bzw. und die Bistabilität stellt das Verhalten der Hystereseschleife dar [50]. Unsere Ergebnisse unterscheiden sich jedoch von früheren Arbeiten zu optomechanischen Zweimodensystemen ohne Berücksichtigung der Hohlraum-Kavitäten-Kopplung J . Daher ist die Kopplungsstärke J spielt eine wichtige Rolle bei der Bistabilität.

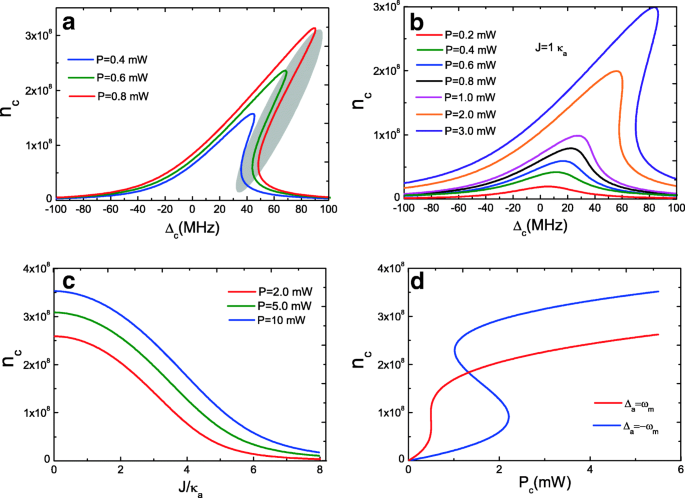
a Mittlere Photonenzahl in der Kavität der optomechanischen Kavität c als Funktion der Hohlraumpumpenverstimmung Δ _c mit drei Pumpleistungen bei J =0. b Mittlere Photonenzahl in der Kavität der optomechanischen Kavität c als Funktion der Hohlraumpumpenverstimmung Δ _c mit mehreren verschiedenen Pumpleistungen unter J =1.0 κ _a . c Mittlere Photonenzahl in der Kavität n _c des optomechanischen Hohlraums c als Funktion von J mit drei Pumpleistungen. d Mittlere Photonenzahl in der Kavität n _c als Funktion von P für Δ _c =Δ _a =ω _m

Wir untersuchen weiter das bistabile Verhalten der optischen Kavität a mit Gl. (11). Abbildung 3a zeigt die Photonenzahl n . in der Kavität _a der gewöhnlichen Kavität a als Funktion der Hohlraumpumpenverstimmung Δ _a =ω _a −ω _p mit Pumpleistung P =0,1 mW, P =1,0 mW und P =10 mW bei J =1.0 κ _a . Es ist offensichtlich, dass die optische Kavität a kann sich aufgrund der Intrakavitäts-Photonenzahl n nicht als bistabiles Verhalten verhalten _a der Kavität a aus Hohlraum c kann die Bistabilität bei niedriger Pumpenleistung nicht aufrechterhalten. Eigentlich nur hohe Pumpleistung P kann a aushöhlen präsentieren bistabiles Verhalten, da nur durch hohe Pumpenleistung angetriebene optomechanische Kavität c , viel mehr Photonen können in den optischen Hohlraum a . einkoppeln . Wir zeichnen auch die mittlere Intrakavitäts-Photonenzahl n _a des optischen Hohlraums a als Funktion der Kopplungsstärke J unter drei Pumpleistungen, wie in Abb. 3b gezeigt. Es ist klar, dass wenn J =0, n _a =0, da keine Kopplung zwischen den beiden Hohlräumen bei J . besteht =0, und unter dieser Bedingung koppelt kein Photon in den optischen Hohlraum a . Mit zunehmender Kopplungsstärke J (Verringerung des Abstands der beiden Kavitäten [26]), die Photonenzahlen in den Kavitäten n _a der gewöhnlichen optischen Kavität a erhöhen, aber nicht immer. Es gibt eine optimale Kopplungsstärke J für den Maximalwert von n _a unter anderer Pumpleistung und dann n _a wird mit zunehmendem J abnehmen . Bemerkenswert ist, dass die Kopplungsstärke J zwischen den beiden Kavitäten einstellbar [26].

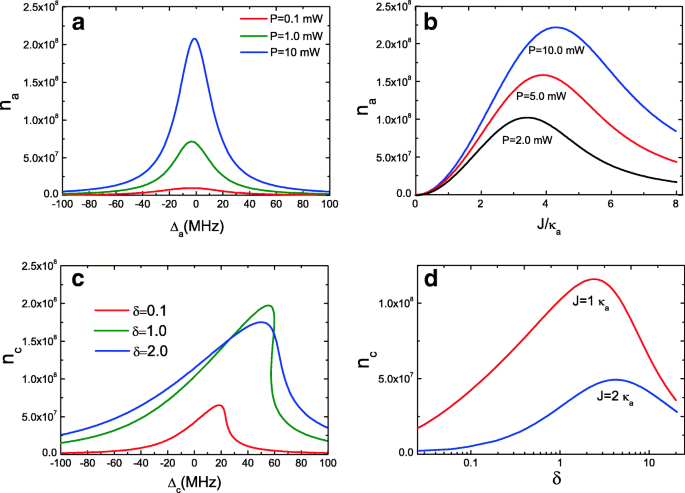
a Mittlere Intrakavitäts-Photonenzahl der gewöhnlichen Kavität a als Funktion der Hohlraumpumpenverstimmung Δ _a mit drei Pumpleistungen bei J =1.0 κ _a . b Mittlere Photonenzahl in der Kavität n _a als Funktion von J mit drei Pumpleistungen. c Mittlere Photonenzahl in der Kavität n _c als Funktion von Δ _c mit drei Verhältnisparametern δ . d Mittlere Photonenzahl in der Kavität n _c als Funktion von δ für zwei J

Außerdem betrachten wir einen Verhältnisparameter δ =κ _c /κ _a (κ _c =ω _c /Q _c und κ _a =ω _a /Q _a ) um die Parameter der beiden Kavitäten zu untersuchen, die das bistabile Verhalten beeinflussen. κ ist die Abklingrate des Hohlraummodus, die mit der Frequenz und dem Qualitätsfaktor des Hohlraums zusammenhängt. Wie wir wissen, ist es aufgrund der Beugungsgrenze schwierig, für einen Resonatormodus gleichzeitig ein hohes Q und ein kleines V zu erreichen. Für eine optische Kavität führt ein kleineres V entsprechend einer größeren Strahlungszerfallsrate zu einem niedrigeren Q. Obwohl verschiedene Arten von Kavitäten ihre eigenen einzigartigen Eigenschaften besitzen, besteht immer noch das Gewicht zwischen einem hohen Q und einem kleinen V. Wenn jedoch durch die Kopplung des ursprünglichen OMS c mit High-Cavity-Dissipation in einen Hilfs-Cavity-Modus a bei hohem Q, aber großem V ändert sich das bistabile Verhalten erheblich. Abbildung 3c zeigt die mittlere Photonenzahl in der Kavität n _c des optomechanischen Hohlraums c als Funktion von Δ _a unter mehreren verschiedenen δ =κ _c /κ _a bei unveränderter Kopplungsstärke J =1.0 κ _a . Wir können feststellen, dass das bistabile Verhalten auftreten kann, aber die Photonenzahl in der Kavität n _c ist klein bei δ =0,1 mit J =2 κ _a , d. h. κ _c =0,1 κ _a was bedeutet Q _c >Q _a . Beim Erhöhen des Verhältnisses δ von δ =1.0 bis δ =2,0, die Photonenzahl in der Kavität n _c erfährt den Wechsel vom bistabilen Verhalten zum nahezu lorentzschen Linienprofil. Das heißt, wenn Q _c <Q _a , wird das bistabile Verhalten unterbrochen, aber es gibt eine optimale Bedingung, d. h. Q _c =Q _a . In Abb. 3d geben wir die Photonenzahl n . in der Kavität an _c als Funktion von δ mit zwei verschiedenen J , und natürlich durch Erhöhen des Verhältnisparameters δ , die Photonenzahlen in der Kavität n _c Zunahme. Wenn es einen optimalen Wert für ein gegebenes J . erreicht , dann n _c verkleinern. Daher kontrolliert man die Resonatorparameter, wie die Zerfallsrate κ oder der Qualitätsfaktor der Kavitäten, kann das bistabile Verhalten kontrolliert werden.

Andererseits untersuchen wir als typisches nichtlineares optisches Phänomen auch den FWM-Prozess mit Gl. (14) im optomechanischen System mit photonischen Molekülen. Abbildung 4 zeigt das FWM-Spektrum als Funktion des Sondenhohlraums a Verstimmung Δ _s =ω _s −ω _a bei Δ _a =Δ _c =0 unter verschiedenen Parameterregimen. Abbildung 4a–d zeigt die Entwicklung der FWM-Spektren bei unterschiedlicher Pumpleistung P bei J =1.0 κ _a . Es ist klar, dass die FWM-Spektren drei Peaks aufweisen, wobei ein Lorentz-Peak in der Nähe von Δ _s =0 und zwei modenspaltende Peaks liegen bei ±ω _m , und die FWM-Intensität nimmt mit zunehmender Pumpleistung ab. Abbildung 4e–h zeigt die Änderung der FWM-Spektren von J =0.5 κ _a zu J =2.0 κ _a bei Pumpleistung P =1,0 mW. Mit zunehmender Kopplungsstärke J von J =0.5 κ _a zu J =2.0 κ _a , ändern sich die FWM-Spektren deutlich. Die Phänomene können mit einem Dressed-State-Bild erklärt werden, das in einem optomechanischen Single-Cavity-System demonstriert wurde [51].

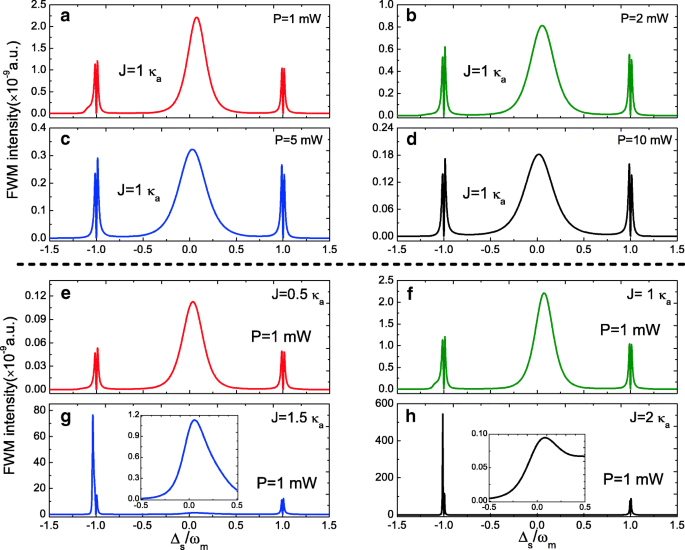
a –d FWM-Intensität als Funktion der normierten Sonden-Pumpen-Verstimmung Δ _s für unterschiedliche Pumpleistung bei J =1.0 κ _a . e –h FWM-Intensität als Funktion von Δ _s für verschiedene J bei Pumpleistung P =1.0 mW

Wir untersuchen dann die FWM-Spektren bei Δ _a =Δ _c 0. Abbildung 5a–d zeigt die FWM-Spektren im roten Seitenband, d. h. Δ _a =Δ _c =ω _m unter einem unveränderten J =1.0 κ _a mit Erhöhung der Pumpleistung von P =1.0 bis P =10mW. In den FWM-Spektren erscheinen zwei normale modenspaltende Peaks, die sich bei ±ω . befinden _m bzw. die FWM-Intensität nimmt mit zunehmender Pumpleistung ab. Abbildung 5e–h zeigt die FWM-Spektren im roten Seitenband, d. h. Δ _a =Δ _c =ω _m unter einer festen Pumpleistung P =2,0 mW mit zunehmender Kopplungsstärke J von J =0.5 κ _a zu J =2.0 κ _a . Offensichtlich steigt die FWM-Intensität mit zunehmender Kopplungsstärke J , und das größere J bedeutet mehr Photonenzahlen, die in den optischen Hohlraum eingekoppelt werden a . Beim Ändern der Verstimmung Δ _a und Δ _c vom roten Seitenband zum blauen Seitenband, d. h. Δ _a =Δ _c =−ω _m , ändert sich die Entwicklung der FWM-Spektren deutlich. Abbildung 5i–l zeigt die FWM-Spektren im blauen Seitenband unter vier verschiedenen Pumpleistungen, und die FWM-Intensität nimmt mit zunehmender Pumpleistung sogar im blauen Seitenband ab. Mit Ausnahme von zwei normalen modenspaltenden Peaks bei ±ω _m , gibt es auch zwei scharfe Seitenbandpeaks in den FWM-Spektren und ihre Lage hängt mit der Pumpleistung zusammen. In Abb. 5m–p diskutieren wir auch die Kopplungsstärke J die die FWM-Spektren unter dem blauen Seitenband beeinflussen. Ob andere scharfe Seitenbandpeaks in den FWM-Spektren erscheinen, hängt von der Kopplungsstärke J . ab .

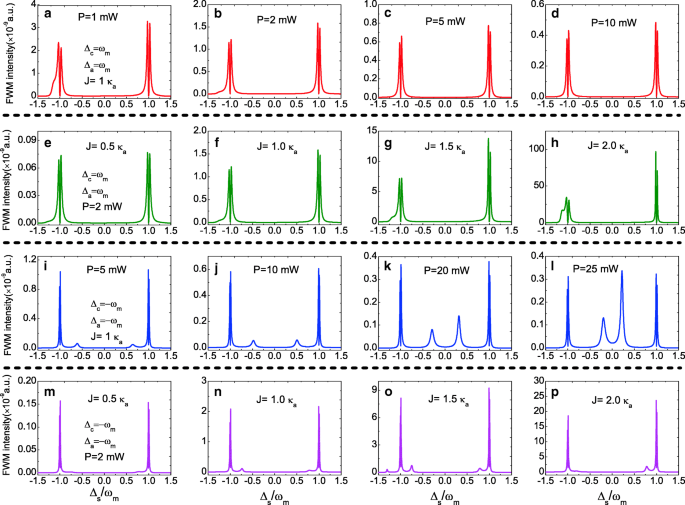
a –d FWM-Intensität als Funktion von Δ _s für unterschiedliche Pumpenleistung P am roten Seitenband (Δ _c =Δ _a =ω _m ) und J =1.0 κ _a . e –h FWM-Intensität als Funktion von Δ _s für verschiedene J unter dem roten Seitenband und der Pumpleistung P =2,0 mW. ich –l FWM-Intensität als Funktion von Δ _s für unterschiedliche Pumpenleistung P am blauen Seitenband (Δ _c =Δ _a =−ω _m ) und J =1.0 κ _a . m –p FWM-Intensität als Funktion von Δ _s für verschiedene J unter dem blauen Seitenband und der Pumpleistung P =2,0 mW

Da der Verhältnisparameter δ =κ _c /κ _a kann die Photonenzahl in der Kavität im zusammengesetzten photonischen Molekül OMS beeinflussen, die FWM-Spektren können durch Kontrolle des Parameters δ . manipuliert werden . Abbildung 6a–h zeigt die FWM-Spektren bei unveränderten Parametern J =2.0 κ _a und P =10 mW unter dem roten Seitenband mit zunehmendem Verhältnis δ von δ =0,05 bis δ =3.0, und die FWM-Intensität nimmt mit zunehmendem Verhältnis δ . ab . Im blauen Seitenband erscheinen andere scharfe Seitenbandpeaks in den FWM-Spektren, wie in Abb. 6i–p gezeigt, und die FWM-Intensität nimmt auch mit zunehmendem Verhältnis δ . ab . Mit der Kontrolle der Resonatorparameter, wie der Zerfallsrate κ oder das Q der Kavitäten, kann die FWM in der zusammengesetzten Photonik-Molekül-OMS einfach erreichen.

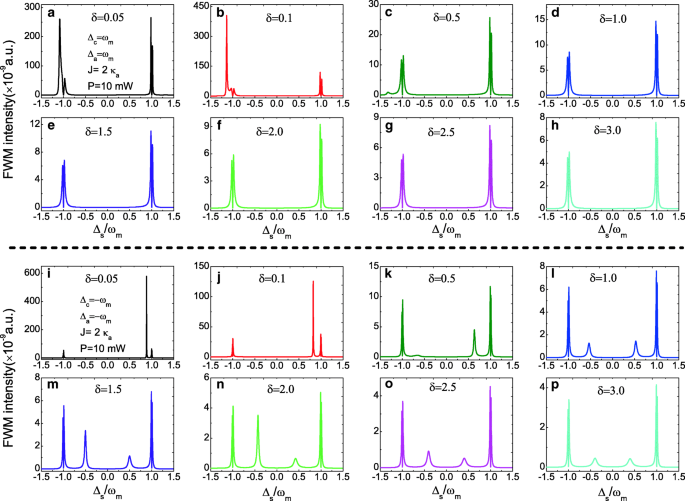
a –h FWM-Intensität als Funktion von Δ _s für mehrere verschiedene Verhältnisparameter δ am roten Seitenband (Δ _c =Δ _a =ω _m ) und J =2.0 κ _a , P =10mW. ich –p FWM-Intensität als Funktion von Δ _s für mehrere verschiedene Verhältnisparameter δ am blauen Seitenband (Δ _c =Δ _a =−ω _m ) und J =2.0 κ _a , P =10 mW

Schlussfolgerung

We have investigated the optical bistability and four-wave mixing in a composite WGM cavity photonic-molecule optomechanical system, which includes an optomechanical cavity with high-cavity dissipation coupled to an auxiliary cavity with high-quality factor. We investigate the optical bistability under different parameter regimes such as the coupling strength J between the two cavities and the decay rate ratio δ of the two cavities in the system. The optical bistability can be adjusted by the pump field driving the optomechanical cavity, and the intracavity photon number in the two cavities is determined by the coupling strength J . Further, we have also demonstrated how to control the FWM process in the photonic-molecule optomechanical system under different driving conditions (the red sideband and the blue sideband) and different parameter conditions (the coupling strength J and the ratio δ ). Numerical results show that the FWM process can be controlled with such parameters. These results are beneficial for better understanding the nonlinear phenomena in the composite photonic-molecule optomechanical system.

Abkürzungen

C-OMS:

Cavity optomechanics systems

FWM:

Four-wave mixing

OMS:

Optomechanics systems

OMIT:

Optomechanically induced transparency

F:

Quality

V:

Volume

WGM:

Whispering gallery mode