Starke Kopplung zwischen einem Quasi-Einzelmolekül und einer plasmonischen Kavität im Einfangsystem

Einführung

In den letzten Jahren war die Verwendung optischer Dipolfallen zum Einfangen und Kühlen von Atomen oder Molekülen eine vielversprechende Technologie, um das Bose-Einstein-Kondensat zu erreichen, grundlegende physikalische Gesetze zu testen und grundlegende physikalische Konstanten genauer zu messen [1–3]. Optische Dipolfallen nutzen hauptsächlich die Gradientenkräfte des einfallenden Lichts, um einen Dipoleffekt auf ein Atom zu erzeugen. Bei den rotverstimmten Fallen werden die Atome dort gefangen, wo die Lichtintensität unter anziehendem Potential am stärksten ist [4]. Aufgrund der Rayleigh- und Raman-Streuung werden die gefangenen Atome einer scheinbaren atomaren Kohärenz und einem Erwärmungseffekt ausgesetzt. Gleichzeitig weist das Kernenergieniveau in der stärksten Lichtposition eine starke optische Frequenzverschiebung auf [1]. Bei den blauverstimmten Fallen [5, 6] hingegen werden die Atome im Bereich der schwächsten Lichtintensität unter Ausschlusspotential gefangen [6–8]. Im Vergleich zu rotverstimmten Fallen kann die Streurate eines Photons mit einer schwachen Intensität des einfallenden Lichts deutlich reduziert werden, was eine stabilere Möglichkeit bietet, die kleinen Partikel einzufangen. Allerdings ist die Konstruktion der blauverstimmten Fallen oft komplex [9, 10]. Oberflächenplasmonenpolaritonen (SPPs) sind Hybridmoden von Lichtwellen, die an Oszillationen freier Elektronen gekoppelt sind, die an der Grenzfläche zwischen einem Dielektrikum und einem Metall begrenzt sind und ein enormes Potenzial für eine breite Palette von Anwendungen im Bereich von THz-Geräten haben [11–14], Materialien [15], Sensoren [16], Meta-Oberfläche [17] und Quanteninformationsverarbeitung [18]. Die Kombination von optischem Trapping mit plasmonischen Strukturen ist eine Möglichkeit, integrierte optische Komponenten zu entwickeln. Chang et al. vorgeschlagen, eine Nanostruktur mit einer kombinierten Nanospitze und Mikroscheibenkavität zum Einfangen von isolierten Atomen zu verwenden [19]; Chenet al. erzielten ein stabiles 3D-Atom-Trapping basierend auf blau verstimmtem Licht in einer Anordnung von plasmonischen Nanolöchern [20]. Eine periodische plasmonische Nanostruktur mit einer Anordnung von Löchern im Subwellenlängenbereich hat interessante optische Eigenschaften, was ein ermutigendes Szenario ist, um ein kleines Teilchen wie ein Atom oder ein Molekül einzufangen.

Eine starke Kopplung zwischen einer plasmonischen Kavität und einem Molekül weckt nicht nur Interesse an der grundlegenden Untersuchung des quantenelektrodynamischen Phänomens, sondern bietet auch gute Aussichten für die Quanteninformationsverarbeitung [21–23]. Plasmonische Hohlräume, die die Stärke der Licht-Materie-Wechselwirkung signifikant erhöhen können, sind ein geeigneter Kandidat, um die starke Kopplung bei Raumtemperatur zu erreichen [24–26]. Die Kopplung eines einzelnen Moleküls mit einer plasmonischen Kavität ist jedoch sowohl in Theorie als auch in Experimenten eine große Herausforderung, da es schwierig ist, die Position des Moleküls im Kopplungssystem zu manipulieren.

In diesem Artikel untersuchen wir theoretisch die starke Kopplung zwischen einem quasi-einzelnen Molekül und einem plasmonischen Hohlraum für jede Einheit eines blauverstimmten Einfangsystems. Das blauverstimmte Einfangsystem besteht aus einem Gold-Nanoloch-Array, und jede Einheit fängt nur ein Molekül ein. Die Finite-Differenz-Zeitdomänen-(FDTD)-Methode wird verwendet, um unsere Struktur zu simulieren, und das Transmissionsspektrum kann erhalten werden. Wenn das Molekül an der schwächsten Stelle gefangen ist, zeigt das Streuspektrum eine Rabi-Aufspaltung, ein Zeichen für ein starkes Kopplungsregime. Die vorgeschlagene Struktur bietet einen möglichen Weg, um die starke Kopplung zwischen einem quasi-einzelnen Molekül und einem plasmonischen Hohlraum im optischen Einfangsystem zu erreichen.

Methoden

Wir entwerfen eine periodische Nanolochstruktur, um das blauverstimmte Einfangen zu erreichen. Unsere Simulationen basieren auf FDTD-Methoden und wir verwenden die EAST FDTD-Software, um unsere Struktur festzulegen und das Übertragungsspektrum und die elektromagnetische Verteilung zu untersuchen. In unserem Modell ist eine Reihe von Gold-Nanolocheinheiten mit einem Radius R in einem zweidimensionalen (2D) Au-Film im X . angeordnet -J Ebene und die Dicke des Au-Films beträgt 400 nm. Die Gitterkonstante L und der Radius R sind 1000 nm bzw. 250 nm. Während unserer Simulation beträgt der Hintergrundindex 1 und das Gitter beträgt 5 nm für jede Richtung. Die periodischen Randbedingungen werden sowohl entlang der X -Achse und Y -Achse. Die perfekte Übereinstimmungsebene wird entlang des Z . festgelegt -Achse. Die Zahl der perfekten Anpassungsschicht beträgt 32. Die Dielektrizitätskonstante von Au wird von Johnson und Christy [27] erhalten. Zirkulares Polarisationslicht wird normalerweise entlang des Z . auf die Oberfläche der vorgeschlagenen Struktur injiziert -Achse, und die Wellenlänge beträgt 696 nm. Ein X -J Planenschreiber ist 400 nm von der vorgeschlagenen Strukturoberfläche entfernt, um die Transmission und ein X . zu berechnen -Z Planenschreiber befindet sich in der Mitte der Struktur, um die elektromagnetische Feldverteilung zu erhalten. Aufgrund der Eigenschaft der Dipolquelle in der FDTD-Simulation [28–30] können wir die Dipolquelle verwenden, um das Molekül zu simulieren. Die Resonanzwellenlänge des Moleküls beträgt 707 nm und die Zerfallsrate beträgt 1,1 × 10 ¹⁴ Hz. In unserer Simulation ist die Übertragung T wird berechnet, indem der Poynting-Vektor über die obere Fläche integriert und auf den in Abwesenheit der Metallstruktur erhaltenen normiert wird [31]. Die in der FDTD-Simulation berechnete Transmission wird als T . bezeichnet =Ich _T /(ich _C +Ich _D ), wobei ich _T ist die elektromagnetische Feldstärke der Übertragung, I _C die elektromagnetische Feldstärke von zirkular polarisiertem Licht ist und I _D ist die elektromagnetische Feldstärke des Dipols.

Ergebnisse und Diskussion

Trapping-Struktur

Eine plasmonische Nanostruktur mit einer Anordnung von Löchern im Subwellenlängenbereich weist einen außergewöhnlichen optischen Transmissionseffekt auf, der das lokale elektrische Feld in der Nähe der Nanolöcher erheblich verstärkt [32–34]. Wir nutzen diesen Effekt auf molekulare Bewegungen. Wenn ein Plasmonenresonanzfeld von der Molekülresonanz blau verstimmt wird, kann eine riesige Abstoßungskraft des Moleküls erzeugt werden und ein Einfangminimum etwa Hunderte von Nanometern von der Strukturoberfläche entfernt erzeugt werden. Wir entwerfen eine periodische plasmonische Nanostruktur, um unseren Ansatz zu demonstrieren, wie in Abb. 1 gezeigt.

Schematische Darstellung der periodischen plasmonischen Nanostruktur

In diesem Abschnitt diskutieren wir nur die Simulationsergebnisse ohne Molekül. Wir verwenden ein zirkulares Polarisationslicht, um die Struktur normalerweise vom Z . zu beleuchten Richtung im Unendlichen, und das Transmissionsspektrum ist in Abb. 2 dargestellt.

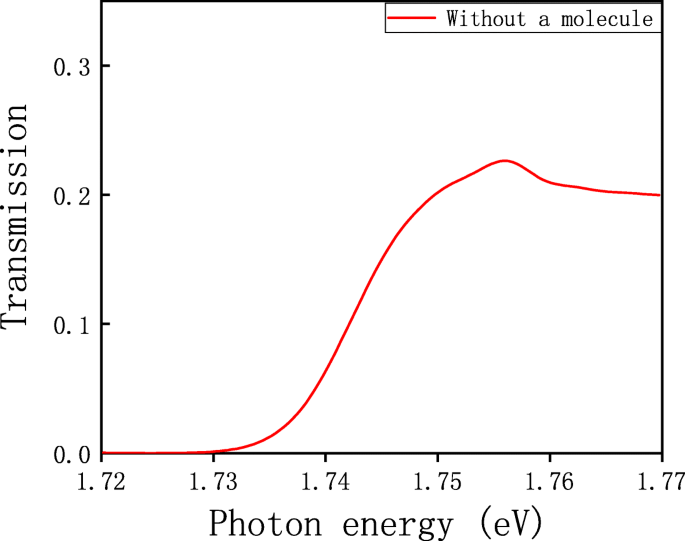
Das Transmissionsspektrum der Struktur ohne Molekül

Bei 707 nm (1.756 eV) wird ein Resonanzpeak beobachtet, der von der Wechselwirkung zwischen den Einheiten (den Löchern) herrührt. Dieser Peak liegt nahe der Wellenlänge der (1, 1)-Ordnung der Wood-Anomalie [35]. Ein Array von Subwellenlängenlöchern weist Bragg-Streuung an den SPPs auf, was einen reziproken Gittervektor des Arrays bewirkt, der die Phasenanpassungsbedingung leicht erfüllen kann [20]. Somit kann einfallendes Licht die SPPs anregen, und diese Art der Anregung von SPPs ist viel einfacher als die Verwendung der Kretschmann-Struktur und wird nicht von der Dicke des Metalls beeinflusst. Um die räumliche Verteilung des elektromagnetischen Feldes des Systems zu untersuchen, zeichnen wir eine Figur von |E | ² Verteilung des X -Z Flugzeug um Y =0 bei der Resonanzwellenlänge von 707 nm, die in Fig. 3a gezeigt ist.

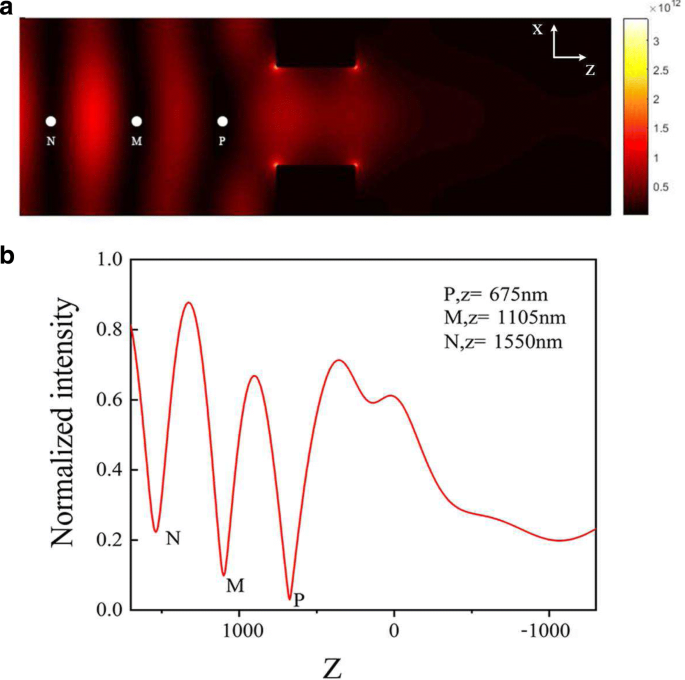
a Elektromagnetische Feldstärke |E | ² Verteilung im X -Z Flugzeug um Y =0 bei λ =696 nm. b Normalisierte Intensitätsverteilungen von |E | ² gegen Z mit X =0 und Y =0 im X -Z Flugzeug

In Abb. 3a gibt es drei Minima von |E | ² bemerkt durch die weißen Punkte P, M und N; das Auftreten dieser drei Minima kann auf die entstehenden Hot Spots zurückgeführt werden, die aus der Nahfeldstreuung von Licht durch eine Anordnung plasmonischer Nanolöcher resultieren. Tatsächlich ist die Verteilung des elektromagnetischen Felds die Überlagerung des Oberflächenplasmonenfelds und des räumlichen elektromagnetischen Felds durch die Nanolöcher. Die Kurve von |E | ² gegen Z bei X =0 und Y =0 im X -Z Ebene ist auch in Abb. 3b eingezeichnet. Gemäß dem Simulationsergebnis der räumlichen elektromagnetischen Verteilung gibt es drei Intensitätsminima, was die blauverstimmte optische Falle impliziert.

Ein Molekül kann durch optische Dipolkräfte mit blau verstimmtem Licht in Minima der elektromagnetischen Feldstärke gefangen werden. In unserer Simulation wird das Molekül als Zwei-Niveau-System behandelt und kann in der FDTD-Simulation als Dipol simuliert werden [28–30]. Das Einfangpotential U _wählen für ein Molekül ist ein abstoßendes optisches Dipolpotential verbunden mit dem elektromagnetischen Feld E , die durch [1, 4] gegeben ist:

Hier, α ist reduzierte Polarisierbarkeit, in unserem Fall α =−7,87×10 ⁻³⁸ F ·m ² [20]. Daher können wir auf der Grundlage der elektromagnetischen Feldstärkeverteilungen die Einfangpotentiale erhalten. Unter Verwendung von Gl. (1) und |E | ² Verteilungen in Abb. 3a berechneten wir das Einfangpotential entlang der Linie mit sowohl X =0 und Y =0 wie in Abb. 4 angezeigt.

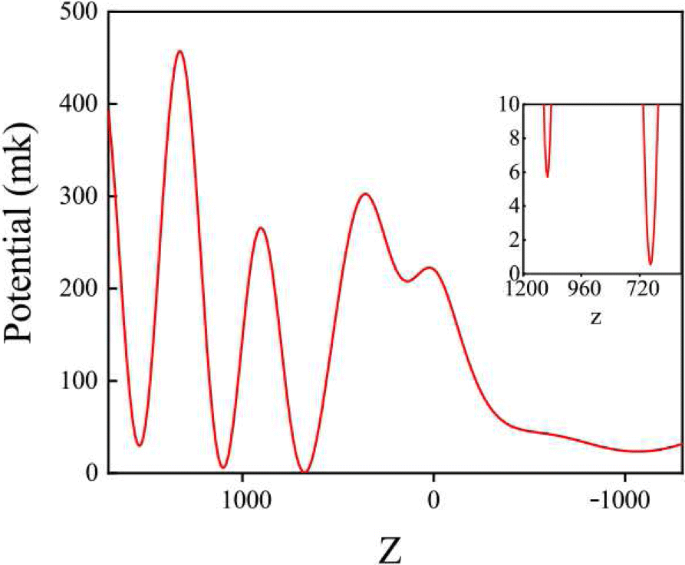
Fangpotenzial in X -Z Flugzeug um Y =0. Das Einfügebild ist die Vergrößerung des niedrigsten Einfangpotentials

In Abb. 4 wissen wir, dass sich die Position mit der niedrigsten Intensität am Punkt P befindet. Hier wird die einfallende Leistung als P . festgelegt _ich =120 mW und das Einfangpotential beträgt 0,53 mK. Chenet al. hat berichtet, dass ⁸⁷ R b können mit dem Einfangpotential von 2,02 mK stabil eingefangen werden [20]. Vergleicht man diese Parameter, könnte unser blau-verstimmtes Einfangsystem ein Rhodaminmolekül mit einem Molekulargewicht von etwa 400 einfangen. Angesichts der obigen Analyse wählen wir die Einfangposition am Punkt (0, 0, 675 nm) und das Schema Diagramm eines in der Struktur gefangenen Moleküls ist in Abb. 5 gezeigt.

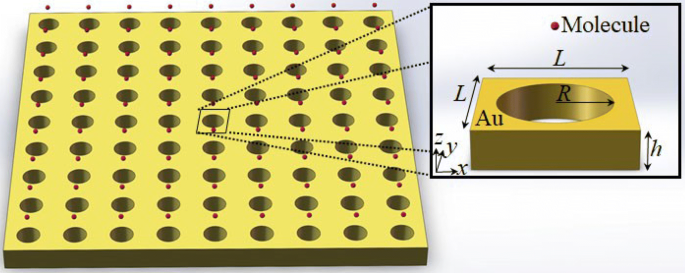
Schematische Darstellung eines in der Struktur gefangenen Moleküls

Starke Kopplung zwischen Struktur und Molekül

Moleküle werden in jede Einheit unserer Struktur eingebracht, um die Licht-Molekül-Wechselwirkung bei starker Kopplung zu untersuchen. Das Molekül kann in FDTD-Simulationen als Dipol behandelt werden. Wir fügen einen Dipol am Potentialminimumpunkt P hinzu, der 275 nm von der Oberfläche entfernt ist, wie in Abb. 3a gezeigt. Die Polarisation des Dipols könnte entlang des X . verlaufen -Achse, das Y -Achse oder das Z -Achse. Die Resonanzwellenlänge des Moleküls beträgt 707 nm (1.756 eV). Zuerst betrachten wir die Polarisation des Dipols entlang des Z -Achse. Das Transmissionsspektrum wird ebenfalls erhalten und das Ergebnis ist in Abb. 6.

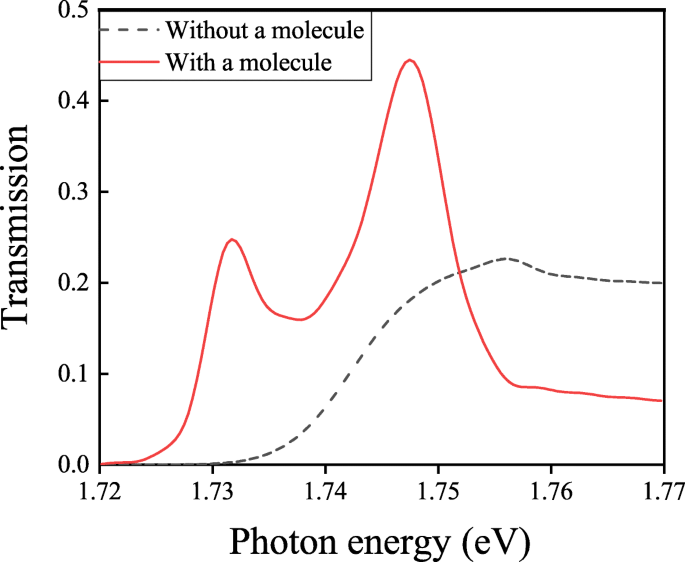
Transmissionsspektren mit und ohne Molekül werden am Punkt P eingefangen

Zum Vergleich ist das Transmissionsspektrum der Struktur ohne Molekül in jeder Einheit auch in Abb. 6 aufgetragen. In Übereinstimmung mit Abb. 6 können wir im Transmissionsspektrum der Struktur mit einem Molekül zwei Aufspaltungspeaks beobachten, die die Rabi-Aufspaltungslinienform und präsentiert das starke Kopplungsphänomen. Einfallendes Licht injiziert nicht nur auf die Oberfläche unserer Struktur, sondern regt das Molekül auch an. SPPs, die durch einfallendes Licht angeregt werden, koppeln mit denen, die vom Molekül um die Arbeitswellenlänge angeregt werden. Diese beiden Arten von SPPs koppeln miteinander und erzeugen zwei Teilungspeaks im Transmissionsspektrum. Die Linienform der Transmissionskurve zeigt das starke Kopplungsphänomen. Im Allgemeinen sind die Frequenzen dieser beiden Aufspaltungspeaks ω _± werden als [36, 37] bezeichnet:

wo ω ₀ ist die Energie unter der Bedingung, dass das isolierte Molekül und der Hohlraum in Resonanz sind, γ _c =4,08×10 ¹³ Hz [38] und γ _m =1.1×10 ¹⁴ Hz sind die Zerfallsraten der plasmonischen Kavität bzw. des Moleküls und g ist die Kopplungskonstante. Starke Kopplung tritt für g . auf>0,5|γ _c −γ _m | und entspricht der Bildung eines gekleideten Zustands mit endlicher Lebensdauer. Für unsere vorgeschlagene Struktur ist die Kopplungskonstante g beträgt 144 meV, während 0,5|γ _c −γ _m | beträgt 143 meV. In früheren Arbeiten wurde die Rabi-Aufspaltung als Ω . bezeichnet =|ω ₊ −ω ₋ | liegt im Bereich von 100 bis 450 meV in den auf J-Aggregat-Metall- oder Molekül-Metall-Hybrid-Nanostrukturen basierenden Strukturen [39, 40]. Die Rabi-Aufspaltung bezieht sich auf die Kopplungsstärke g , die von\(\sqrt {N/V}\) abhängt, wobei N ist die Anzahl der Moleküle und V ist die Moduslautstärke [37]. In unserer Arbeit gibt es nur ein Molekül in jeder Einheit der vorgeschlagenen Struktur und das Modenvolumen V ist so groß, dass die Rabi-Aufspaltung Ω etwa 16 meV beträgt, ist diese Aufspaltung vergleichbar mit einer starken Kopplung in Metall-Halbleiter-Hybrid-Nanostrukturen [41] und Metall-2D-Materialsystemen [42]. Wir haben auch die starke Kopplung der Struktur mit der Polarisation des Moleküls entlang der X . untersucht -Achse und das Y -Achse bzw. Die Simulationsergebnisse sind in Abb. 7 dargestellt.

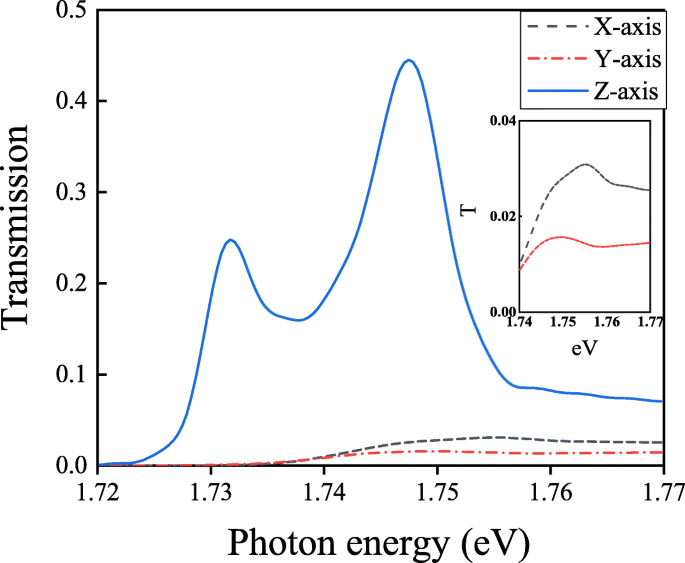
Transmissionsspektren mit einem in X-, Y- bzw. Z-Richtung polarisierten Molekül

In Abb. 7 erscheinen zwei Aufspaltungspeaks (710 nm, 1,747 eV; 717 nm, 1,717 eV) nur in der Struktur mit der Polarisation des Moleküls entlang des Z -Achse. Das Molekül polarisiert entlang des X -Achse oder das Y -Achse zeigt ein starkes kollektives Verhalten vor der Kopplung mit Au-Nanokavitäten oder Au-Nanohole-Arrays. Das kollektive Verhalten S _k des Moleküls polarisiert entlang der X -Achse oder das Y -Achse kann nach der Methode des gekoppelten Dipols berechnet werden [43]:

wo k ₀ ist der Wellenvektor im Vakuum, θ der Winkel zwischen zwei Dipolen ist und r =n L , n =1, 2, 3... Hier mit der Bedingung von \( \lambda =\frac {L}{\sqrt {i^{2}+j^{2}}}\) (i , j =0, 1, 2,..., aber beide i und j ungleich 0 sind), ist das Kollektivverhalten recht groß, was eine Singularität in Gl. (3) [35, 43]. Es zeigt einen resonanten Einbruch im Transmissionsspektrum. Für das Molekül, das entlang des X . polarisiert ist -Achse oder das Y -Achse ist das Kollektivverhalten zu groß, um die Kopplung zwischen Molekül und Plasmonenhöhle zu schwächen. Wir sehen nur die Ordnung der Wood-Anomalie [35] mit der Ordnung (1, 1) im Transmissionsspektrum um die Wellenlänge 707 nm (1.756 eV), die starke Kopplung konnte nicht auftreten. Daher polarisiert nur das Molekül entlang des Z -Achse in unserer vorgeschlagenen Struktur das starke Kopplungsphänomen erzeugen kann. Wenn die Resonanzwellenlänge des Moleküls geändert wird, kann die starke Kopplung im blauverstimmten Einfangsystem auch durch die folgenden Schritte erreicht werden. Zum einen kann je nach Resonanz des Moleküls die Gitterkonstante des Nanohole-Arrays festgelegt werden. Zum anderen lässt sich auch die Arbeitswellenlänge des blauverstimmten Trapping-Systems bestimmen, die von der Gitterkonstante des metallischen Nanohole-Arrays abhängt. Drittens wird die elektromagnetische Feldverteilung erhalten, um die Einfangposition zu finden. Schließlich bringen wir das Molekül an der besten Einfangposition, um das Transmissionsspektrum zu berechnen und die Transmission mit der Linienform der starken Kopplung kann erhalten werden.

Schlussfolgerung

Zusammenfassend entwerfen wir ein metallisches plasmonisch blauverstimmtes Einfangsystem und untersuchen das starke Kopplungsphänomen zwischen einem quasi-einzelnen Molekül und dem Einfangsystem. In FDTD-Simulationen verwenden wir eine Dipolquelle als Molekül und können anhand der elektromagnetischen Feldverteilungen die beste Position finden, um nur ein einzelnes Molekül in der Struktur einzufangen. Durch Berechnung der Transmission der vorgeschlagenen Struktur, ob das Molekül eingefangen wurde oder nicht, finden wir, dass es im Transmissionsspektrum zwei Aufspaltungspeaks gibt, wenn das Molekül in der Struktur eingefangen ist, während nur ein Peak beobachtet wird, wenn das Molekül nicht eingefangen ist . Die beiden Aufspaltungspeaks zeigen an, dass die starke Kopplung stattgefunden hat. Daher können wir das blauverstimmte Einfangsystem so entwickeln, dass eine starke Kopplung in einer nanoplasmonischen Struktur erreicht wird, die potenzielle Anwendungen in der Quanteninformationsverarbeitung hat.

Abkürzungen

FDTD:

Zeitbereich mit endlicher Differenz