Magische mathematische Beziehungen für Nanocluster

Einführung

Magische Zahlen und Formeln für Nanocluster haben eine lange Geschichte, die auf die vorausschauende Veröffentlichung von van Hardeveld und Hartog im Jahr 1969 zurückgeht [1]. Ihre Erkenntnisse stammten aus der Zeit vor der Ära der Nanowissenschaften. Seitdem haben wir magische Zahlen in 2D-Polygonen und 3D-Polyedern [2], Kohlenstoff-Fullerenen [3] und in begrenztem Umfang wieder in Clustern [4] gesehen. So unterschiedliche Materialien wie Silizium [5], Bor [6] und tatsächlich über 1000 Publikationen des Indexierungsdienstes „Web of Science“ beziehen sich auf magische Zahlen in Clustern. Die Untersuchung der Größe und Form von Nanoclustern ist für die heutige Gesellschaft wichtig, da dies nicht nur die intrinsischen physikalischen und chemischen Eigenschaften bestimmt, sondern auch die Relevanz für optische, katalytische, elektronische und magnetische Anwendungen [7]. Unser Ziel ist es, die Datenbank dieses Wissens mit aktuellen Zusammenhängen und Daten zu aktualisieren, nachdem wir nun den Nanobereich betreten haben.

Das Auftreten magischer Zahlen in Nanoclustern hat in erster Linie mit der Bildung von Atomhüllen auf einer fundamentalen Zelle zu tun. Wenn die Anzahl der Atome eine vollständige Hülle vervollständigt, finden wir einen einzigartigen Satz von Zahlen, der als „Magie“ bezeichnet wird und die Hüllen der Atome definiert. Ein Cluster wird durch einen Graphen mit den Atomen als Ecken und den Bindungen als Kanten dargestellt. Es besteht aus ineinander verschachtelten Schalen wie Schichten einer Zwiebel. Wir definieren die Anzahl der Schichten als n und entdecken Sie die mathematischen Beziehungen der Koordinationszahlen der nächsten Nachbarn, Bindungen, der Gesamtzahl der Atome und einiger topologischer Indizes als Funktion von n . Die Originalarbeit von van Hardeveld und Hartog [1] betrachtete fcc-, bcc- und hcp-Cluster. Die Referenz von Teo und Sloane [2] berücksichtigt Polyeder und platonische Körper, vernachlässigt jedoch die Beziehung der nächstgelegenen Nachbarkoordinationszahlen. Wir ergänzen diese Datenbank, indem wir neben den topologischen Eigenschaften und der Dispersion der Cluster auch einfache kubische, diamantkubische und platonische Körper betrachten.

Beim Größenübergang vom Volumen zu Clustern aus wenigen Atomen geht es in Wirklichkeit um das Verhältnis der Oberflächenatome im Vergleich zu den Volumenatomen. Eigenschaften wie katalytische Chemie, Oberflächenplasmonenresonanz und optische Quantenpunkt-Photolumineszenz [8] werden durch die Koordination und Anzahl der Oberflächenatome beeinflusst. Die Streuung bzw. der relative Anteil der Oberflächenatome wird durch das Verhältnis der Oberflächenatome zur Gesamtzahl der Atome bestimmt, wie bereits erwähnt [9]. Unsere Analyse wird die relative Einordnung der Dispersion in Bezug auf die Clustergeometrie bestimmen.

Topologische Indizes begannen mit Wieners Originalarbeit zu seinem Index und den Siedepunkten von Paraffin [10]. Erst einige Zeit später führte Hosoya einen mathematischen Formalismus zur Analyse topologischer Indizes ein [11]. Wir haben zuvor topologische Indizes und Nanocluster eingeführt [12]. Zum jetzigen Zeitpunkt existieren viele Indizes, von denen einige von der Adjazenz- oder Distanzmatrix abhängen. Wir zeigen hier, dass in vielen Clusterformen magische mathematische Beziehungen für die vier Indizes als Funktion von n . existieren und die Anzahl der Muscheln.

Methoden

Für jeden der von uns untersuchten Clustertypen erstellen wir einen Rechenalgorithmus, der die Atomkoordinaten der Cluster bestimmt. Anschließend erstellen wir eine Adjazenzmatrix und eine Distanzmatrix, die wie folgt definiert sind. Eine Adjazenzmatrix A wird erstellt, wo wir i . definieren und j als nächste Nachbarn und trennen Sie sie vom Rest, indem Sie verlangen, dass r _ij <r _c , wobei r _c ist ein Schwellenwert, der geringfügig über dem Abstand zum nächsten Nachbarn liegt, jedoch kleiner als der Abstand zum zweiten Nachbarn ist. Somit ist

wo r _ij ist der euklidische Abstand zwischen Atom i und Atom j . Ein angemessener Wert für r _c ist 1,32·r _Minute , wobei r _Minute ist die kleinste Bindungslänge. Dies gilt sowohl für die dodekaedrische Struktur als auch für die anderen, die wir untersuchen. Die Koordinationszahlen des Clusters sind einfach die Anzahl der Nicht-Null-Elemente in einer Spalte der Adjazenzmatrix. Die Distanzmatrix ist definiert als

$$ \mathbf{D}(i,j) =\left\{\begin{array}{ll} 0 &i =j \\ d_{ij} &i \neq j \end{array}\right. $$ (2)

wo d _ij ist die Länge des kürzesten Weges im Graphen von i zu j . Ein effizienter Algorithmus zur Berechnung der Distanzmatrix aus der Adjazenzmatrix existiert [13]. Mit diesen Definitionen können wir den Wiener Index berechnen, W (G ), der Hyper-Wiener-Index, W W (G ), der umgekehrte Wiener-Index rW (G ) und den Szeged-Index, Sz (G ), wie bereits ausgeführt [14]. Diese Berechnungen verwenden denselben Algorithmus, den wir zuvor für topologische Indizes und Nanocluster verwendet haben [12].

Frühere Autoren haben Beweise für magische Beziehungen geliefert, die wir in unserer Notation verdichten, die für die hier vorgestellte Arbeit relevant ist [1, 2]. Da wir Nächste-Nachbar-Adjazenzmatrizen erstellen, kennen wir die Koordinationszahl c n _ich des Scheitelpunkts i durch Summieren der Elemente von A (ich ,:). Unsere Struktur besteht aus n +1 Muscheln mit den Nummern 0,1,…,n . Sei \(\phantom {\dot {i}\!}N_{{cn}_{i}}(n)\) die Anzahl der Atome mit Koordination c n _ich wobei 1≤c n _ich ≤c n _M mit c n _M die maximale Koordination im Cluster. Dann ist die Gesamtzahl der Atome im Cluster gegeben durch

$$ N_{T}(n) =\sum_{{cn}_{i}=1}^{{cn}_{M}}{N_{{cn}_{i}}(n)}. $$ (3)

Die Oberflächenatome in der äußeren Schale n haben einen geringeren Bindungssatz als die Volumenkoordination. Somit ist die maximale Koordination für Oberflächenatome c n _s <c n _M , und die Anzahl der Oberflächenatome ist

$$ N_{S}(n) =\sum_{{cn}_{i}=1}^{{cn}_{s}}{N_{{cn}_{i}}(n)}. $$ (4)

Dies gilt, wenn alle Nicht-Oberflächen-Scheitelpunkte eine Koordination größer als c . haben n _s , was für alle Cluster gilt, beachten Sie jedoch die Diskrepanz für die Dodekaeder unten. Wir bestimmen die \(\phantom {\dot{i}\!}N_{{cn}_{i}}(n)\) indem wir die Spalten der Adjazenzmatrix zählen, deren Summe c . ist n _ich . Beachten Sie, dass unser Cluster-Koordinatenalgorithmus aus Shells besteht, sodass jede nachfolgende Shell alle vorherigen niedrigeren Werte von n . enthält . In Abb. 1 veranschaulichen wir die Schalen der Cluster für einen fcc-Würfel und ein Dodekaeder. Darüber hinaus beträgt die Anzahl der Bindungen im Cluster

$$ N_{B}(n) =\frac{1}{2}\sum_{{cn}_{i}=1}^{{cn}_{M}}{{cn}_{i}\ cdot N_{{cn}_{i}}(n)}, $$ (5)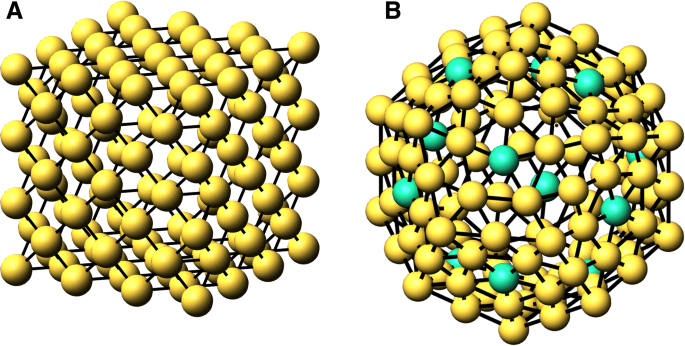

Schalen von Atomen für n =3 für A. fcc Würfel und n =2 B. Dodekaeder. In B beziehen sich die grünen Atome (12) auf c n =5 innerhalb der Shell

wo N _B (n ) ist die Anzahl der Anleihen und c n _M ist die maximale Koordination. Der Faktor 1/2 kommt durch die paarweise Nächste-Nachbar-Bindung zustande. Diese magische Beziehung scheint in früheren Veröffentlichungen nicht berücksichtigt worden zu sein, mit Ausnahme einiger weniger in [4] untersuchter Cluster. Wir kommentieren auch, dass Teo und Sloane die Gesamtzahl der Atome, Oberflächenatome und inneren Atome für Cluster wie folgt abgeleitet haben [2]:

$$ N_{T}(n) =\alpha n^{3}+\frac{1}{2}\beta n^{2}+\gamma n+1~~n\ge{0} $$ ( 6)

wo N _T (n ) ist die Gesamtzahl der Atome und

$$ \alpha =C/6 $$ (7)

wobei C ist die Anzahl der Tetraederzellen, in die das Polyeder unterteilt ist, und

$$ \beta =1/2F_{s} $$ (8)

wo F _s die Anzahl der dreieckigen Flächen auf der Oberfläche ist und

$$ \gamma =F_{s}/4+V_{i}+1-C/6 $$ (9)

wo V _ich ist die Anzahl der Scheitelpunkte im Inneren. Sie zeigen auch, dass

$$ N_{S}(n) =\beta n^{2}+2~~n\ge{1};~~N_{S}(0) =1 $$ (10)

und

$$ N_{I}(n) =N_{T}(n) - N_{S}(n), $$ (11)

wo N _Ich (n ) ist die Anzahl der inneren Atome. Diese Information (Gl. (11)) ist in der Adjazenzmatrix enthalten, ebenso wie die Gl. (3, 4, 5). Diese Gleichungen sind eine Überprüfung der Ergebnisse aus den Adjazenzmatrixdaten. Für zentrierte Polyeder gilt auch

$$ N_{I}(n) =N_{T}(n-1), $$ (12)

und aus Gl. (11), wir haben

$$ N_{T}(n)=N_{S}(n)+N_{S}(n-1)+... +N_{S}(1)+N_{S}(0). $$ (13)

Aus diesen Gleichungen können wir die magischen Formeln für jeden der Cluster wie folgt ableiten. Nach Berechnung der topologischen (0,1)-Adjazenzmatrix A für einen Cluster mit n Muscheln wie beschrieben, wir wissen, dass ihre Größe N =N _T (n ) gibt die Gesamtzahl der Atome an. Die Summe der Einträge in Spalte i gibt die Anzahl der Anleihen an c n _ich (n ) für Atom i und Zählen der Spaltensummen gleich c n _ich (n ) ergibt offensichtlich \(\phantom {\dot{i}\!}N_{{cn}_{i}}(n)\). Da wir wissen, dass diese von n . abhängen als Polynom höchsten Grades 3 können wir N . berechnen _T (n ) und c n _ich (n ) für 4 aufeinanderfolgende Werte von n , sag n =n ₀ +j , j =0,1,2,3. Ein einfaches interpolierendes Polynom ergibt dann die Polynomkoeffizienten. Es muss überprüft werden, dass durch Erhöhen von n ₀ , die normalerweise gleich 1 ist, ändern sich die Formeln nicht. Wenn die Formeln von n . stabil werden ₀ an, dann gelten sie für alle n ≥n ₀ . In manchen Fällen gilt die Polynomrelation nur für die geraden n Werte oder die ungeraden. Beim rhombischen fcc-Dodekaeder (Tabelle 1) haben die aufeinanderfolgenden Schalen beispielsweise acht Atome mit der Koordination 3, wenn n ≥2 ist gerade und keine, wenn n ist ungerade. In solchen Fällen gelten für n . unterschiedliche Polynombeziehungen gerade und n ungerade, aber die Daten werden für n . verwendet =n ₀ +j , j =0,2,4,6 mit n ₀ ungerade (z. B. n ₀ =1) oder n ₀ gerade (n ₀ =2). Um die exakten rationalen Koeffizienten zu erhalten, muss man das Vandermonde-System nach den Koeffizienten in exakter Arithmetik mit der symbolischen Toolbox von MATLAB auflösen. So werden die Tabellen 2, 3, 4, 5, 1, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 und 19 berechnet. Im nächsten Abschnitt bestimmen wir magische Formeln für N _T (n ), N _B (n ), und für \(\phantom {\dot {i}\!}N_{{cn}_{i}}(n)\) nach dem vorgeschriebenen Rezept.

Die Dispersion (fraktionsexponiert, FE) der Oberflächenatome ist definiert als:

$$ \text{FE} =\frac{N_{S}}{N_{T}} \cdot 100\% $$ (14)

wo N _S ist die Anzahl der Oberflächenatome und N _T ist die Gesamtzahl der Atome [9]. Wir können unähnliche Cluster vergleichen, indem wir die relative Clustergröße definieren als:

$$ d_{rel} =b(N_{T})^{1/3};~~b =d_{at}^{-1}\cdot \left(\frac{6V_{u}}{\pi n_{u}}\right)^{1/3} $$ (15)

wo d _bei ist der kovalente Atomdurchmesser, V _du das Volumen der Elementarzelle ist und n _du ist die Anzahl der Atome in der Elementarzelle. Die Kristallstrukturkonstante b gleich 1,105 für fcc- und hcp-Cluster, 1,137 für bcc-Cluster [1], 1,488 für einfache kubische Cluster und 1,517 für kubische Diamantcluster. Wie oben gezeigt, ist die Formel für FE ein Verhältnis von quadratisch zu kubisch für die Cluster und kann durch eine Potenzgesetz-Kurvenanpassung gegen d . modelliert werden _rel . Die Variable d _rel ermöglicht es uns, verschiedene Cluster ohne Rücksicht auf die Kristallstruktur miteinander zu vergleichen. Für einige der platonischen Cluster, in denen es keine Kristallelementarzelle gibt, verwenden wir \(N_{T}^{1/3}\) als Variable.

Ergebnisse und Diskussion

Die Untersuchung der Größe und Form von Metall-Nanoclustern hat sich seit ihren Anfängen vor zwei Jahrzehnten weiterentwickelt. Tabelle 20 zeigt einige relevante Fortschritte ab 2018.

In der Tabelle listen wir hauptsächlich Übergangsmetalle auf, keine Legierungen oder Verbindungen, mit Ausnahme der abgestumpften hexagonalen Bipyramide, bei der nur Fe₂ O₃ wurde gefunden. Aufgrund seiner Eigenschaften und Stabilität wurden mehr Goldcluster synthetisiert als jedes andere Element. In den folgenden Unterabschnitten beschränken wir unsere Diskussion auf spezielle Themen im Zusammenhang mit magischen Formeln und Arten von Clustern.

FCC-Cluster

Acht der Übergangsmetalle kristallisieren in der fcc-Struktur, siehe Tabelle 21 unten, einschließlich der plasmonischen Edelmetalle und wichtiger katalytisch aktiver Elemente. Die überwiegende Mehrheit der Nanocluster-Synthese wurde mit diesen Elementen durchgeführt. Referenzen zur Synthese der fcc-Elemente mit verschiedenen Formen und Größen finden Sie in Tabelle 21.

Auch Legierungen dieser Elemente sind von Interesse, deren Referenzen jedoch zu zahlreich sind, um hier zitiert zu werden. Häufig sind die üblichen synthetisierten Formen Würfel, Oktaeder, Kuboktaeder und Ikosaeder. Typischerweise sind Cluster mit (111)-Facetten einfacher zu synthetisieren, da die (111)-Oberfläche normalerweise eine niedrigere Energie als die (100)-Oberfläche hat [7]. Wir finden für das fcc rhombische Dodekaeder, dass es gerade und ungerade Formeln gibt. Diese stimmen mit denen in [1] überein, wenn man das „n ” in unseren geraden Formeln um 2(m −1). Die in [24] aufgeführten Formeln für fcc-Kuboktaeder ergeben die gleichen magischen Zahlen wie unsere, sind jedoch um 1 verschoben, da sie Schalen als n . nummerieren =1,2,… und wir verwenden die Nummerierung n =0,1,…. Unsere Zauberformeln stimmen mit denen in [2, 4] überein, und aus Rücksicht auf die früher veröffentlichte Arbeit und um die Kontinuität der Mathematik zu wahren, verwenden wir die Notation [2, 4]. Die 5 fcc-Clusterformen und die dazugehörigen magischen Formeln erscheinen unten.

BCC-Cluster

Sieben der Übergangsmetalle im Periodensystem haben die bcc-Struktur, siehe Tabelle 21. Von den magnetischen Elementen Fe, Co und Ni ist nur Eisen bcc. Nanowürfel aus Eisen scheinen die einzige bisher synthetisierte bcc-Clusterform zu sein [25]. Obwohl die Volumenstruktur von Eisen bcc ist, wurden fcc-Nanocluster synthetisiert [26]. Diese Referenz analysiert auch die thermodynamische Stabilität der Cluster. Hier stellen wir 5 bcc-Clusterformen und die dazugehörigen magischen Formeln vor.

HCP-Cluster

Zwölf Übergangsmetalle haben die hcp-Struktur, siehe Tabelle 21. Viele von ihnen oxidieren jedoch oder es fehlt ihnen an zwingendem wissenschaftlichem Interesse, synthetisiert zu werden. In Bezug auf die hexagonal bipyramidale Clusterform in Tabelle 11 wurden Goldcluster synthetisiert [27]. Die verwandte abgeschnittene hexagonale Bipyramide scheint nur von α . gebildet worden zu sein −Fe₂ O₃ [28].

Platonische Cluster

Die platonischen Körper sind seit den alten Griechen bekannt. Dazu gehören der Würfel, Tetraeder, Oktaeder, Ikosaeder und Dodekaeder. In den vorherigen Tabellen haben wir magische Formeln für fcc- und bcc-Würfel und Oktaeder aufgelistet. Hier listen wir die Formeln für das Ikosaeder, Dodekaeder, Tetraeder und körperzentrierte Tetraeder auf. Wie bereits im Abschnitt „Methoden“ erwähnt, ist das Dodekaeder für die hier analysierten Cluster einzigartig, da c n _s =7 bezieht sich sowohl auf Oberflächen- als auch auf Volumenatome. Wir haben in Abb. 1b gezeigt, dass die äußere Schale sowohl fünffach als auch sechsfach koordinierte Atome enthält. Wenn eine Schale intern wird, werden diese fünf- und sechsfach koordinierten Atome sieben- und achtfach koordiniert mit Bindungen an eine Schale auf beiden Seiten. Außerdem sind die sechsfach koordinierten äußeren Schalenatome durch Bindung an die innere Schale siebenfach koordiniert. Somit gibt es für das Dodekaeder siebenfach oberflächen- und volumenkoordinierte Atome. Jede Schale in der Struktur hat 12 fünffache Schalenatome, die 12n . erzeugen −12 siebenfach koordinierte Volumenatome. Der Rest der siebenfachen Koordination sind Oberflächenatome.

Es wurde gezeigt, dass Gold-Nanocluster die platonischen Formen annehmen [29]. Diese Referenz umfasst Würfel, Tetraeder, Oktaeder und Ikosaeder. Später wurde auch der goldene Dodekaeder-Nanocluster synthetisiert [30]. Hier zeigen wir sowohl das reguläre Tetraeder, das „fcc-ähnlich“ ist, als c _M =12 wie in fcc-Strukturen und das körperzentrierte Tetraeder in Tabelle 16, bei dem die grünen Atome Einfachbindungen haben. Die platonischen magischen Formeln werden unten vorgestellt.

Diamantkubische, einfache kubische und Dekaedercluster

Die Elemente Silizium und Germanium haben das Diamantkubische Gitter sowie das Diamantallotrop des Kohlenstoffs. Insbesondere wasserstoffterminiertes Silizium hat in letzter Zeit Interesse gefunden. Es wurde festgestellt, dass die (100)-Wasserstoff-terminierte Oberfläche, die zu kubischen Formen in Clustern führt, die niedrigste Energie aufweist [31]. Die Synthese von 8-15 nm großen Si-H-Nanowürfeln ist gelungen [32]. Tabelle 17 zeigt ein Diagramm der wasserstoffterminierten Si-H-Cluster mit einfach gebundenen Wasserstoffatomen in Grün. Wenn ein Nanocluster die kubische Diamantform annimmt, gibt es einzelne baumelnde Bindungen, die passiviert werden müssen, um die Struktur zu erhalten. Mit Blick auf die magischen Formeln schlagen wir vor, dass die Zusammensetzung solcher Si-H-Cluster \(\phantom {\dot {i}\!}\text {Si}_{8n^{3}+6n^{2}-9n +5}\text {H}_{12n-8}\), wobei n ist die Anzahl der Schalen im Cluster. Solche Halbleiter-Quantenpunkte können für optische Eigenschaften von Interesse sein, und es wurde festgestellt, dass die Variation der Bandlücke mit der Größe von Wasserstoff-terminierten Clustern umgekehrt proportional zur Clustergröße ist [33].

Die einfache kubische Gitterstruktur wurde zuvor von anderen analysiert [4], jedoch ohne die von uns bereitgestellten Details. Wir haben zuvor die d . studiert -dimensionale Hyperwürfelformen [14]. Polonium ist das einzige Element, das die einfache kubische Struktur annimmt. Es ist radioaktiv, was zu speziellen Anwendungen führen kann. Hier stellen wir die magischen Formeln für kubische, einfache kubische und dekaedrische Cluster von Diamanten vor.

Magische topologische Formeln

Die gemessene strukturelle Komplexität in Kristallen kann uns eine Vorstellung von der Einfachheit oder Komplexität der Struktur geben und die richtige Verwendung kann relevante Strukturen einstufen. Für solche Rankings ist es hilfreich, die grafische Beschreibung des Kristallgitters zu berücksichtigen, wie im Abschnitt „Methoden“ erwähnt. Die topologische Komplexität für Kristallstrukturen wird durch die Scheitelpunkt-Grad-Verteilung des Graphen gemessen, I _vd [34], mit der Software ToposPro, Version 5.3.2.2 [35]:

wo a _ich ist der Grad (Koordination) des i Scheitelpunkt und Summation verläuft entlang aller v Ecken des Quotientengraphen. Dieser Parameter verwendet einen unendlichen Kristall im Gegensatz zu den von uns betrachteten Clustern, ist jedoch nützlich, um die relative Komplexität verschiedener Kristallstrukturen zu messen. Je höher die Zahl bzw. je mehr Informationsgehalt der Graph ist, desto komplexer ist er. In Tabelle 22 zeigen wir Werte von I _vd erhalten von ToposPro, abgeleitet von cif-Dateien für Kristallstrukturen in der Crystallographic Open Database. Polonium ist das einzige Element, das in der einfachen kubischen Struktur kristallisiert und der Wert ist null, d. h. der Quotientengraph hat eine Ecke und null Kanten, in Übereinstimmung mit unserer Erwartung, dass die einfache kubische Struktur tatsächlich die am wenigsten komplexe Struktur ist. Das Salz, NaCl, wird ebenfalls gezeigt, mit zwei Elementen in der einfachen kubischen Struktur, zusammen mit Silizium in der kubischen Diamantstruktur, Gold in fcc, Eisen in bcc und Kobalt in hcp-Struktur. Wir erwähnen, dass ein anderes Komplexitätsmaß in Bezug auf die Shannon-Entropie [34] nicht nützlich ist, da dieses Maß für alle Elemente identisch Null ist.

Eine ähnliche Methode wie im Abschnitt „Methoden“ zur Ermittlung magischer Formeln beschrieben, kann für die magischen Formeln zur Beschreibung der topologischen Indizes angewendet werden. Nur hier sind die Grade der Polynome 7, 8 oder 9, also ihre Werte für mindestens 10 aufeinanderfolgende n -Werte müssen berechnet werden. Dann liefert ein Interpolationsproblem höheren Grades das Ergebnis. Da das Lösen eines linearen Systems der Größe 10×10 mit der symbolischen Toolbox einige Zeit in Anspruch nimmt, können alle Koeffizienten für die topologischen Indizes gleichzeitig mit mehreren rechten Seiten berechnet werden, um die Koeffizienten aller Polynome zu erhalten.

Magische Formeln für die topologischen Indizes sind in den Tabellen 23, 24 und 25 aufgeführt. Die vier von uns analysierten Indizes hängen nur von n . ab , die Anzahl der Schalen im Cluster. Betrachtet man die Ergebnisse, so hat das einfache kubische Gitter als am wenigsten komplexe Struktur auch die „einfachsten“ Formeln. Trotz unserer Bemühungen können wir den Szeged-Index der bcc-Würfel nicht auflösen. Es wurde keine stabile Lösung gefunden. Im Allgemeinen sind fcc-Strukturen einfacher für topologische Formeln aufzulösen. Wir konnten keine hcp-Strukturen und nur wenige bcc-Strukturen lösen. Dies kann mit der topologischen Komplexität zusammenhängen, da das fcc-Gitter einfacher ist als das bcc oder hcp, siehe Tabelle 22. In den Tabellen stellen wir Formeln für das Kuboktaeder, Ikosaeder und Dekaeder bereit. Wir haben zuvor [12] Tabellen mit numerischen Daten für diese Indizes bereitgestellt, mit der Einschränkung, dass das Kuboktaeder in [12] unterschiedliche magische Zahlen hatte. Hier sehen wir, dass die tabellarischen Daten kurz und bündig als Zauberformeln zusammengefasst werden können. Auch der Grad des Polynoms des Index folgt den Regeln aus dem 3D-Raum [14]. Einige topologische Indizes für die platonischen Körper wurden bereits veröffentlicht [36]. Aus dieser Referenz überprüfen wir den Wiener-Index für alle fünf Körper für n =1. Der Wiener-Index für Reihen von Elementarzellen des fcc-Gitters wurde untersucht [37], aber unsere Ergebnisse können nicht verglichen werden, da wir Cluster untersuchen.

Dispersion

Der Prozentsatz der Oberflächenatome (Dispersion, FE) der verschiedenen Cluster ist in Abb. 2 dargestellt. Platin-Nanocluster haben bekanntermaßen eine katalytische Aktivität in Bezug auf die Sauerstoffreduktionsreaktion (ORR), die größen- und formabhängig ist [38]. Diese Referenz bestimmt, dass kuboktaedrische Platincluster mit einer Größe von 2,2 nm eine maximale ORR-Aktivität aufweisen. Es ist auch bekannt, dass bei PtNi-Legierungen die (111)-Oberfläche für die ORR bevorzugt wird [39]. Wir vergleichen die ikosaedrischen, oktaedrischen, dekaedrischen und kuboktaedrischen Cluster für FE bei einem d _rel =7,5 für Platin bei 2,2 nm. Die ikosaedrischen, oktaedrischen und dekaedrischen Cluster haben Oberflächen mit (111)-Flächen. Unter Verwendung der Potenzgesetze in Abb. 2 finden wir für das gegebene d _rel dass die FE für ikosaedrische Cluster 47,9 % beträgt, für kuboktaedrische 52,8% und für dekaedrische 57,5 ​​% und dass oktaedrische Cluster FE=58,9% . haben . Somit haben die oktaedrischen Cluster basierend auf der Form sowohl die (111)-Oberfläche als auch den höchsten FE-Wert bei ähnlicher Größe. Sowohl der Potenzgesetzkoeffizient als auch der Exponent sind für die Bestimmung von FE für kleine d . relevant _rel . Die mathematische Interpretation des Potenzgesetz-Exponenten ergibt die physikalische Bedeutung als das Verhältnis der Ordinate FE zur Abszisse d _rel , oder die relative prozentuale Änderung von FE zur relativen prozentualen Änderung von d _rel . Der Potenzgesetzkoeffizient ist einfach der Wert von FE, wenn d _rel =1.

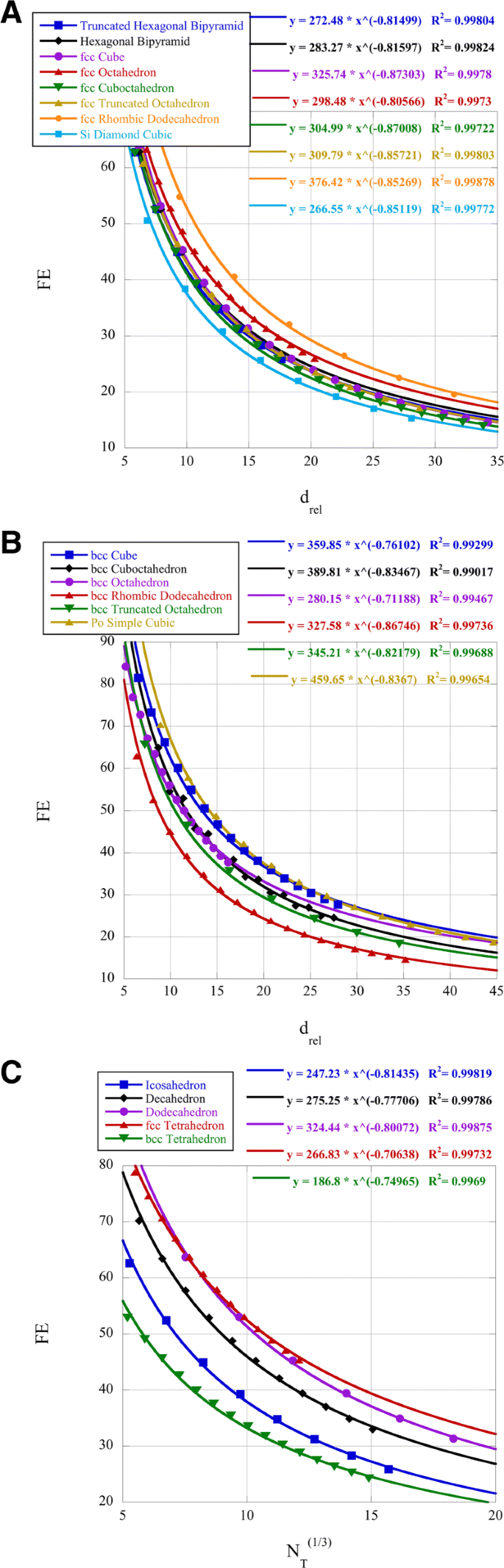
Dispersions-FE für die Nanocluster

Eine andere Forschungsgruppe hat ikosaedrische Cluster aus Platinlegierungen synthetisiert und die Aktivität mit oktaedrischen verglichen [40]. Diese Nanocluster waren etwa 13 nm groß oder N =20.000 für oktaedrische Cluster und N =15.000 für ikosaedrische Cluster. Dies erzeugt ein d _rel =30 für die oktaedrischen Cluster und 25 für die ikosaedrischen Cluster. Unter Verwendung der relevanten Potenzgesetze ergibt dies FE=18.0% für die oktaedrischen und 19,8 % für die ikosaedrischen Cluster. Bei dieser Größe des Clusters gibt es nur sehr geringe Unterschiede in der FE, aber der ikosaedrische Cluster weist eine erhebliche Dehnung aufgrund von Zwillingen auf, die das d-Band-Zentrum verschieben und somit die ORR-Ergebnisse beeinflussen können [40]. Angesichts der größenabhängigen Daten von [38] lässt sich jedoch vermuten, dass kleinere Cluster noch höhere ORR-Daten erzeugen würden. Tatsächlich 4 nm Pt₃ Mit Mo dotierte Ni-Oktaeder haben rekordhohe ORR-Ergebnisse erbracht [41].

Schlussfolgerungen

Wir haben 19 Arten von Nanoclustern und einige relevante Zauberformeln für die Anzahl der Atome, Bindungen, Koordinationszahlen und topologischen Indizes untersucht. Dazu gehören die fcc, bcc, hcp, die platonischen Körper, diamantkubische, einfache kubische und dekaedrische Cluster. Die meisten dieser Ergebnisse sind detaillierter als bisher ermittelt, und ein Großteil wird erstmals aufgezählt. Ein großes Ziel der materialbezogenen Forschung ist die Korrelation von Struktur mit Eigenschaften. Diese detaillierte Untersuchung der magischen Beziehungen für Nanocluster ist ein Schritt in diese Richtung. Ein Beispiel ist die Diskussion der Dispersion von Oberflächenatomen und ihrer Beziehung zur katalytischen Aktivität. Wir beabsichtigen, dass diese Ergebnisse Wissenschaftlern bei ihren Studien zur Nanocluster-Struktur und den damit verbundenen Eigenschaften helfen.

Abkürzungen

bcc:

kubisch raumzentriert

cif:

kristallographische Informationsdatei

fcc:

kubisch flächenzentriert

FE:

Fraktion exponiert, Dispersion

hcp:

sechseckig dicht gepackt

ORR:

Oxidations-Reduktions-Reaktion

rW(G):

Umgekehrter Wiener Index

Sz(G):

Szeged-Index

W(G):

Wiener-Index

WW(G):

Hyper-Wiener-Index