Magische mathematische Formeln für Nanoboxen

Zusammenfassung

Hohle Nanostrukturen stehen im Vordergrund vieler wissenschaftlicher Bemühungen. Diese bestehen aus Nanoboxen, Nanokäfigen, Nanoframes und Nanotubes. Wir untersuchen die Mathematik der atomaren Koordination in Nanoboxen. Solche Strukturen bestehen aus einem hohlen Kasten mit n Muscheln und t äußere Schichten. Die magischen Formeln, die wir herleiten, hängen sowohl von n und t . Wir finden, dass Nanoboxen mit t = 2 oder 3, oder Wände mit nur wenigen Schichten haben im Allgemeinen volumenkoordinierte Atome. Die Vorteile einer geringen Koordination in Nanostrukturen treten nur dann auf, wenn die Wanddicke viel dünner ist als normalerweise synthetisiert. Der Fall, in dem t = 1 ist einzigartig und hat unterschiedliche magische Formeln. Solche niedrig koordinierten Nanoboxen sind für eine Vielzahl von Anwendungen von Interesse, darunter Batterien, Brennstoffzellen, plasmonische, katalytische und biomedizinische Anwendungen. Anhand dieser Formeln ist es möglich, die Oberflächendispersion der Nanoboxen zu bestimmen. Wir erwarten, dass diese Formeln nützlich sind, um zu verstehen, wie die atomare Koordination mit n . variiert und t in einer Nanobox.

Einführung

Nanoboxen wurden ursprünglich um 2002 synthetisiert [1, 2]. Eine Nanobox unterscheidet sich von einem Nanokäfig dadurch, dass letzterer poröse Wände hat. Außerdem unterscheiden sich beide von einem Nanorahmen dadurch, dass der Nanorahmen eine Struktur (Rahmen) ist, die aus dem niedrig koordinierten Umriss des Clusters besteht. Solche anisotropen polyedrischen Strukturen können durch galvanische Verschiebungsreaktionen erzeugt werden [3, 4]

$$\begin{array}{l}\\ {\hbox{Anode}}:yA_{(s)}\rightarrow yA_{({{\rm aq}})}^{x+}+xye_{({{ \rm aq}})}^{-} \\ {\hbox{Kathode}}:xB_{({{\rm aq}})}^{y+} + xye_{({{\rm aq}})} ^{-} \rightarrow xB_{(s)} \\ {\hbox{Voll\,Reaktion}}:yA_{(s)}+xB_{({{\rm aq}})}^{y+} \rightarrow yA_{({{\rm aq}})}^{x+}+xB_{(s)} \\ \end{array}$$ (1)

wo ein Nanocluster mit Metall A wird von einer wässrigen Metalllösung B . opferbereit ausgehöhlt , das ein höheres Reduktionspotential hat und den hohlen Körper von Element B creates erzeugt . Halbreaktionen treten an Anode und Kathode einer elektrochemischen Zelle auf, was zu der vollständigen kombinierten Reaktion wie oben führt [5]. In einigen Fällen haben Wissenschaftler die galvanische Verschiebung mit der Bildung von Hohlräumen über die Kirkendall-Fick-Diffusion von Metallen und Leerstellen kombiniert [6]. Für spezifische Fälle existieren Modelle für diese Aktivität, und es wurde über In-situ-Elektronenmikroskopieexperimente berichtet [7, 8]. Andere Synthesemethoden umfassen chemisches Ätzen [9], Ionenaustausch [10] und Metall-organische Gerüste (MOFs) [11, 12]. Eine aktuelle Übersicht über Synthesemethoden erwähnt, dass noch anisotrope Cluster im Größenbereich \(2

Solche Hohlstrukturen haben eine geringe Koordination, was sie für Batterien [12], Brennstoffzellen [14], plasmonische [15], katalytische [16] und biomedizinische Anwendungen [17] interessant macht. Frühere Analysen zeigen, dass für katalytische Anwendungen ein Koordinationsansatz gilt [18], während es für die Energiespeicherung nur einige Hinweise mit Ergebnissen der Dichtefunktionaltheorie (DFT) gibt, die darauf hindeuten, dass ausgewählte Facetten wichtig sind [19]. Wir verwenden eine zuvor abgeleitete Methode aus der Adjazenzmatrixanalyse [20, 21], um die atomare Koordination einer Box mit n . zu entdecken Schalen und einer Wandstärke von t Schichten. Diese Analyse zeigt, dass eine Nanobox mit t = 2 oder 3 hat eine Massenkoordination und daher sind die Vorteile einer geringen Koordination nur für Nanoboxen mit dünneren Wänden vorhanden, als allgemein für notwendig erachtet wird. Die von uns verwendeten Methoden quantifiziert die atomare Koordination durch magische Zahlen und Formeln für dreizehn Arten von Nanoboxen.

Methoden

Der Schlüssel zu unserer Analyse durch Koordinationsmethoden ist die Erstellung einer Adjazenzmatrix aus den Atomkoordinaten der Nanobox. Eine solche Matrix wird wie folgt erstellt. Wir definieren i und j als nächste Nachbarn, und trennen sie vom Rest, indem Sie verlangen, dass die Bindungslänge \(r_{ij} $${\mathbf{A}}(i,j)=\left\{ \begin{array}{ll} 1 &{\quad}\hbox { if } r_{ij} beschreibt die Adjazenzmatrix für den Cluster und

$${\mathbf{E}}(i,j)=\left\{ \begin{array}{ll} r_{ij} &{\quad}\hbox { if } \, r_{ij} beschreibt die euklidische Matrix für die Box. Wir verwenden die euklidische Matrix, um den Durchmesser zu bestimmen, D , (nm) für die Nanoboxen.

Da wir Nächste-Nachbar-Adjazenzmatrizen erstellen, kennen wir die Koordinationszahl $\hbox {cn}_i$ von Knoten i durch Summieren der Elemente von ${{\mathbf{A}}}(i,:)$. Unsere Struktur besteht aus $n+1$ Schalen mit den Nummern 0, 1, ..., n , mit t äußere Schichten. Sei $N_{{\rm cn}_i}(n,t)$ die Anzahl der Atome mit der Koordination $\hbox{cn}_i$ wobei $1\le \hbox{cn}_i\le \hbox{cn}_M$ mit $\hbox{cn}_M$ der maximalen Koordination in der Nanobox. Dann ist die Gesamtzahl der Atome in der Nanobox gegeben durch

$$N_T(n,t) =\sum_{{\rmcn}_i=1}^{{\rmcn}_M}{N_{{\rmcn}_i}(n,t)}.$$ (4)

Die Oberflächenatome in der äußeren Hülle (oder im Inneren) der Nanobox, n haben einen geringeren Bindungssatz als die Volumenkoordination. Somit ist die maximale Koordination für Oberflächenatome $\hbox{cn}_s <\hbox{cn}_M$, und die Anzahl der Oberflächenatome ist

$$N_S(n,t) =\sum_{{\rmcn}_i=1}^{{\rmcn}_s}{N_{{\rmcn}_i}(n,t)}.$$ (5)

Dies gilt, wenn alle Nicht-Oberflächenknoten eine Koordination größer als $\hbox{cn}_s$ haben, was für alle fcc-, bcc- und hcp-Cluster gilt. Wir bestimmen $N_{{\rm cn}_i}(n,t)$ durch Zählen der Spalten der Adjazenzmatrix, deren Summe $\hbox {cn}_i$ ist. Beachten Sie, dass unser Cluster-Koordinatenalgorithmus aus Shells besteht, sodass jede nachfolgende Shell alle vorherigen niedrigeren Werte von n . enthält . Darüber hinaus beträgt die Anzahl der Anleihen in der Box

$$N_{{\rm B}}(n,t) =\frac{1}{2}\sum _{{\rm cn}_i=1}^{{\rm cn}_M}{\hbox{ cn}_i\cdot N_{{\rm cn}_i}(n,t)},$$ (6)

wobei $N_{{\rm B}}(n,t)$ die Anzahl der Bindungen und $\hbox {cn}_M$ die maximale Koordination ist. Der Faktor 1/2 kommt durch die paarweise Nächste-Nachbar-Bindung zustande.

Da wir wissen, dass diese Gleichungen von n . abhängen , t als Polynom höchsten Grades 3 können wir $N_{{\rm cn}_i}(n,t)$ für 4 aufeinanderfolgende Werte von n . berechnen , sagen wir $n=n_0+j$, j = 0, 1, 2, 3. Ein einfaches interpolierendes Polynom ergibt dann die Polynomkoeffizienten. Es muss überprüft werden, dass sich die Formeln durch Erhöhen von $n_0$, das normalerweise gleich 1 ist, nicht ändern. Werden die Formeln ab $n_0$ stabil, dann gelten sie für alle $n\ge n_0$. Um die exakten rationalen Koeffizienten zu erhalten, muss man das Vandermonde-System nach den Koeffizienten in exakter Arithmetik auflösen.

Beachten Sie, dass in den magischen Formeln für Nanoboxen $n> t$ gilt, so dass entgegen jeder Erwartung die Box durch eine geeignete Wahl von t . aufgefüllt wird wird die ursprünglichen magischen Formeln für die vollständigen festen Cluster nicht neu erstellen. Diese magischen Formeln sind nützlich, um die mesoskaligen Eigenschaften von Clustern und Boxen oder Käfigen zu modellieren. Vollständige Formelsätze wurden ursprünglich für neunzehn Clustertypen abgeleitet. In diesem Manuskript leiten wir magische Formeln für dreizehn Arten von Nanoboxen ab.

In den folgenden magischen Formeln finden wir, dass die Massenkoordination entweder für t . auftreten kann = 2 oder t = 3 Schichten Schalendicke. Die meisten sind für Ebenen, bei denen t = 2; Ausnahmen sind der FCC-Würfel, der Kuboktaeder, der Ikosaeder und der BCC-Würfel und der abgeschnittene Würfel. Im letzteren Fall erscheint die Massenkoordination nur für t = 3 Schichten. Für die folgenden Daten werden die Tabellen der magischen Formeln von einer Abbildung einer „halben Box“ begleitet, um das Innere der Nanoboxen zu zeigen. Daneben befindet sich ein Farbbalken, der die Koordination und Anzahl dieser in Klammern anzeigt.

Ergebnisse und Diskussion

Um die Anwendbarkeit magischer Formeln zu skizzieren, skizzieren wir, wie das katalytische Verhalten von der Koordination und solchen Formeln abhängen kann. Wir definieren G als die größenabhängige Gibbs-Energie des Clusters. Da Adatome an die äußeren Schalenatome gebunden sind, kommt es zu einem Anstieg von G das heißt Adsorptionsenergie und wird als $\Delta G$ bezeichnet. Diese lässt sich auf verschiedene Koordinationstypen der Atome auf der äußeren Schale aufteilen, die zu Adatomen binden. Zum Beispiel fügt ein Knickatom der Adsorptionsenergie einen Betrag $\Updelta G_{k}$ hinzu. In ähnlicher Weise fügt ein Kantenatom $\Delta G_{e}$ hinzu, während ein Facettenatom $\Delta G_f$ beisteuert, dann [18]:

$$\Updelta G=\sum_{o\in\{f,e,k\}} \Updelta G_o N_o$$ (7)

wobei $N_o$ die Anzahl der Atome in der äußeren Schale des angegebenen Typs ist. Die Gesamtzahl der Atome in der äußeren Schale, die an Adatome gebunden sind, ist definiert als $N_s=N_f+N_e+N_k$, was zu:

$$\begin{ausgerichtet}\Delta G=&{} \Delta G_f\cdot (1-f_e-f_k)+\Delta G_e\cdot f_e+\Delta G_k\cdot f_k \\&\quad {\hbox{where} } \,\,f_o=N_o/N_s, \,\,o\in \{e,k\},\end{ausgerichtet}$$ (8)

mit dem Gibbs-Energieanteil, ausgedrückt durch die Kanten- und Knickstellen, die explizite Koordinationen für spezifische Strukturen aufweisen. Dies zeigt, dass magische Formeln bei Oberflächenreaktionen eine Rolle spielen, durch Kanten- und Knickkoordinationen und deren Formeln. Beachten Sie, dass Gl. (8) gilt für die Adsorption an on-top-Plätzen, andernfalls werden nicht alle Adatome an Atome in der äußeren Schale gebunden. In einem solchen Modell haben die Knickstellen magische Formeln, die mit der Anzahl der Schalen konstant sind, n , Kantenstandorte haben Formeln, die mit n . linear sind , und Facettenseiten haben quadratische Formeln mit n . Genauer gesagt sind die Knickstellen die am niedrigsten koordinierten Formeln, die Kantenstellen sind die zweitniedrigsten koordinierten und Facettenstellen haben cn = 8 für (100)-Facetten und cn = 9 für (111)-Facetten.

Es können zwei fundamentale Beziehungen pro Partikel angewendet werden. Für die Gibbs-Energie und die Adsorptionskonstante $K_{{\rm a}}$ gilt:

$$K_{{\rm a}}={\exp } \left( -\frac{\Delta G}{RT}\right) ,$$ (9)

wo R ist die Gaskonstante und T ist die Temperatur in Kelvin. Darüber hinaus werden Brønsted-Evans-Polanyi-Beziehungen häufig in der homogenen und heterogenen Katalyse verwendet [18, 22] unter Verwendung einer Beziehung für die Reaktionskonstanten k und Gleichgewichtskonstanten K wie folgt:

$$k=gK^{\alpha},\quad 0<\alpha <1,$$ (10)

wo g und $\alpha$ (Polanyi-Parameter) sind Konstanten. Der Polanyi-Parameter ist einheitslos und ein echter Bruch, wie er ursprünglich von Brønsted [23] angegeben wurde. Wir haben dann:

$$k=k'_{a}{\exp} \Bigl (-\alpha \bigl ({f_n^{e}\cdot \chi_{_e}({D_n}) +f_n^{k}\cdot \chi_{_k}({D_n})}\bigr)\Bigr),$$ (11)

$$\begin{ausgerichtet} &\chi_{_e}(D)=\frac{\Delta G_e(D)-\Delta G_f(D)}{RT},\\&\chi_{_k}(D )=\frac{\Updelta G_k(D)-\Updelta G_f(D)}{RT}, \end{ausgerichtet}$$ (12)

und

$$k'_{a}=g\exp \left( -\alpha \frac{\Delta G_f}{RT}\right) .$$ (13)

Diese Analyse zeigt, dass die Bestimmung eines katalytischen Modells eine Methode zur Berechnung der Gibbs-Energie erfordert. Bekannte katalytische Reaktionen wie der zweistufige und der Langmuir-Hinshelwood-Mechanismus wurden in Betracht gezogen [24].

FCC-Nanoboxen

Flächenzentrierte kubische Strukturen sind die häufigste Form für Nanocluster und Nanoboxen. Dies ist die Struktur der Metalle mit interessanten Eigenschaften, wie der Edelmetalle mit plasmonischen Eigenschaften und der katalytischen Edelmetalle. Da Gold ein hohes Reduktionspotential von 1,50 V (siehe Gl. 1) gegenüber der Standard-Wasserstoffelektrode (SHE) [5] hat, ist es eines der am einfachsten zu synthetisierenden Metalle als Nanobox oder Nanokäfig. Gold-Nanoboxen oder Nanokäfige wurden in kubischer [1], Kuboktaeder- [25], Ikosaeder- und Dekaeder-[26], Oktaeder-[27] und Tetraeder-[28]-Form gebildet.

Wir können die ungefähre Größe dieser Nanoboxen bestimmen, indem wir einen Koordinationsansatz für die nächste Nachbarbindungslänge r . verwenden (cn) [29],

$$r(cn) =\frac{2r_{{\rm B}}}{\left( 1+\exp \left( \frac{12 - \langle cn \rangle_c)}{8\cdot \langle cn \rangle _c}\right) \right) }.$$ (14)

Dabei ist $r_{{\rm B}}$ die Bulk-Bindungslänge für Gold (0,2884 nm) und $\langle cn \rangle _c$ die durchschnittliche Koordination des Clusters. Wir finden eine lineare Beziehung zwischen D und n , die Anzahl der Cluster-Shells, wie in Tabelle 1 gezeigt:

$$D(n)=a\cdot r_{{\rm B}} \cdot n + b.$$ (15)

Wir verwenden Nanoboxen mit t = 3, da die Formeln mit t . variieren , und wir möchten eine gewisse Massenkoordination erreichen. Zur Berechnung von D (n ) verwenden wir den maximalen Abstand zwischen Atomen im Cluster, abgeleitet aus der euklidischen Matrix. Beachten Sie, dass D (n ) ist eine empirische Formel, abgeleitet von Daten (variiere n und berechnen D ) und ist als solche nicht bewiesen.

Diese Beziehungen erzeugen Durchmesser in Übereinstimmung mit anderen Daten aus der DFT. Für die massiven Kuboktaeder mit N gleich 55, 561 und 923 erhalten wir Durchmesser von 1,12 nm, 2,85 nm und 3,43 nm. Dies ist im Vergleich zu den veröffentlichten DFT-Ergebnissen für 55 Atome mit 1,1 nm [30], für 561 Atome mit 2,7 nm [31] und für 923 Atome mit 3,5 nm [30] günstig. Die magischen Formeln für einige fcc-Nanoboxen sind unten tabellarisch aufgeführt (Tabellen 2, 3, 4, 5, 6, 7, 8).

Ikosaeder- und Dekaeder-Nanoboxen

Siehe Tabellen 9 und 10.

Diamant und einfache kubische Nanoboxen

Die kubische Diamantgitterstruktur wird von einem Allotrop aus Kohlenstoff sowie den Elementen Silizium und Germanium gebildet. Auch einige kubische Verbindungen bilden diese Struktur, wie kubisches Eisenoxid, tetraedrisches Diamantmaghemit $\gamma$-Fe₂ O₃ . Die Bindungslänge für Fe-O in tetraedrischem Diamantmaghemit $\gamma$-Fe₂ O₃ = 0,186 nm [32]. Dies führt zum Durchmesser der Diamantcluster D (n ) wie unten:

$$D(n) =3,3984\cdot n_{{\rm B}} \cdot n - 0,21194.$$ (16)

Laut Referenz [12] bildeten sich Mikroboxen aus kubischem Eisenoxid und hatten interessante Lithiumspeicherfähigkeiten. Uns ist kein vollständiges Koordinationsmodell für die Energiespeicherung bekannt, aber wie oben erwähnt, deuten die DFT-Ergebnisse darauf hin, dass die Aktivität von der Facettenorientierung abhängen kann [19]. Ein solches Modell der Speicherabhängigkeit von der Koordination existiert derzeit nicht, wie wir es für die Katalyse haben. Aus Gleichung (16) oben (erstellt mit t = 4), eine Microbox benötigt ungefähr n = 1600 Muscheln für Diamant-Maghemit. Magische Formeln für die Diamant- und einfache kubische Gitterstruktur sind unten aufgeführt (Tabellen 11, 12).

BCC-Nanoboxen

Siehe Tabellen 13, 14 und 15.

HCP-Nanoboxen

Siehe Tabelle 16.

Der Fall t = 1

Der Sonderfall t = 1 ist einzigartig und hat als solche unterschiedliche magische Formeln. Wir untersuchen diesen Fall für einige der oben genannten Nanoboxen. Nanoboxen mit ultradünnen Wänden wurden mit kubischen [33], oktaedrischen [16] und ikosaedrischen Formen [34] gebildet. Nach den folgenden magischen Formeln ist die kubische Nanobox mit t = 1 hat die niedrigste Koordination. Platin hat ein relativ hohes Reduktionspotential von 1,18 V gegenüber dem SHE, sodass es durch galvanischen Austausch gebildet werden kann, siehe Gl. (fünfzehn]. Die Eigenschaften der Oxidations-Reduktions-Reaktion (ORR) einiger dieser Platin-basierten Nanokäfige weisen jedoch darauf hin, dass Strukturen mit (111)-Facetten im Gegensatz zu (100)-Facetten bessere ORR-Massenaktivitäten aufweisen [35].

Somit hat das Ikosaeder mit 20 (111) Facetten die beste ORR-Massenaktivität, gefolgt vom Oktaeder und zuletzt dem abgestumpften Würfel. Diese Eigenschaft des katalytischen Verhaltens von der Facettenorientierung, die Vorrang vor der Koordinationszahl hat, wird durch die nachstehenden Tabellendaten belegt. Mit anderen Worten, wie in den folgenden Tabellen erwähnt, hat der Würfel mit (100)-Facetten die niedrigsten magischen Koordinationszahlen mit vier und fünf, jedoch haben Oktaeder und Ikosaeder mit (111)-Facetten und größeren magischen Formeln eine bessere ORR-Aktivität. Diese Eigenschaft wird auch in Nanoclustern nachgewiesen, wo DFT-Ergebnisse die Dominanz der (111)-Facetten [36] bestätigen, insbesondere für PtNi-Legierungen (Tabellen 17, 18, 19, 20, 21).

Dispersion

Angesichts der Bedeutung von Kanten- und Knickstellen im Vergleich zu Facetten für die katalytische Aktivität haben wir die Oberflächendispersion für einige der von uns untersuchten Nanoboxen bestimmt. Die (100)-Facetten haben cn = 8, während die (111)-Facetten cn = 9 haben. Dies kann einen Einblick in die Gründe für die individuelle polyedrische Aktivität im Vergleich zwischen den Nanoboxen geben. In Abb. 1 unten zeichnen wir die Oberflächendispersion $D_{{\rm s}} =(N_{{\rm e}} + N_{{\rm k}}) / N_{{\rm S}} \cdot 100\%$. In dieser Beziehung ist $N_{{\rm k}}$ die Anzahl der Knick- oder Eckplätze und $N_{{\rm e}}$ die Anzahl der Kantenplätze. Wie in Abbildung 1 zu sehen ist, weisen Nanoboxen mit (111)-Oberflächen im Gegensatz zu (100)-Oberflächen eine höhere Dispersion auf, was die Bevorzugung der katalytischen Aktivität der (111)-Facette glaubhaft macht.

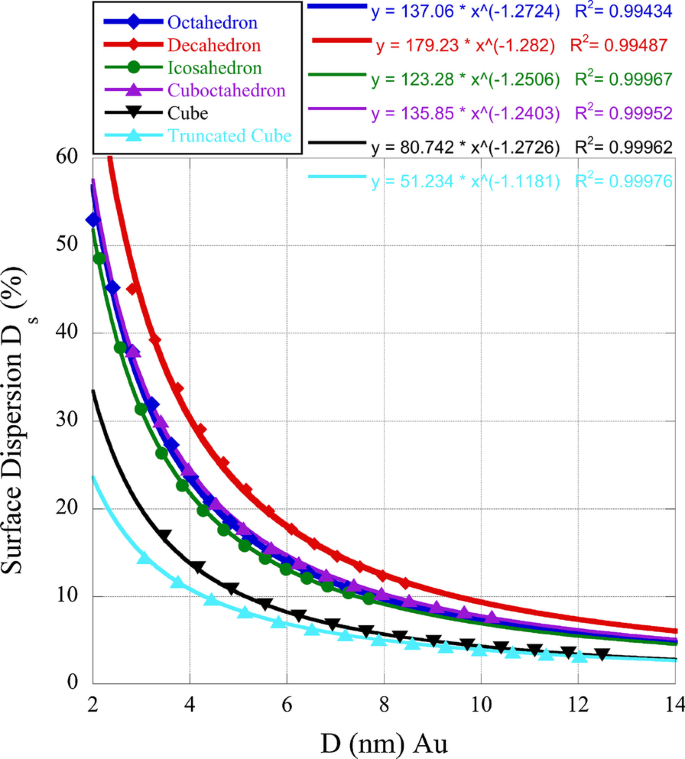
Oberflächendispersion von Gold-Nanoboxen

Schlussfolgerung

Zusammenfassend haben wir die erste detaillierte mathematische Beschreibung magischer Formeln für Nanoboxen präsentiert. Der Fall der Schalendicke, t = 1 unterscheidet sich von $t>1$ und wir stellen die Daten für einige dieser Fälle tabellarisch zusammen. Die Formeln für die Koordination, Anzahl der Atome und Anzahl der Bindungen sind alle aufgezählt. Wir stellen fest, dass die Bulk-Koordination für Layer auftritt, bei denen t = 2 oder 3 und ist daher viel dünner als normalerweise synthetisiert. Die Vorteile der geringen Koordination werden nur bei sehr dünnen Wänden erreicht. Wir erwarten, dass diese Ergebnisse für die Modellierung und experimentelle Arbeit nützlich sind.

Verfügbarkeit von Daten und Materialien

Die Datensätze, die die Schlussfolgerungen dieses Artikels unterstützen, können beim entsprechenden Autor angefordert werden.

Abkürzungen

bcc:: Körperzentriert kubisch
fcc:: Flächenzentriert kubisch
hcp:: Sechseckig dicht gepackt
DFT:: Dichtefunktionaltheorie
Sie:: Sekundäre Wasserstoffelektrode

Quantitative Bewertung der zellulären Internalisierung von polymeren Nanopartikeln in Kehlkopfkrebszellen und Immunzellen für eine verbesserte Wirkstoffabgabe Ein Dual-Vier-Quadranten-Fotodetektor basierend auf schwarzem Nanometer-Silizium im Nahinfrarotbereich

Nanomaterialien