charakteristische Impedanz

Die parallelen Drähte von unendlicher Länge

Nehmen wir jedoch an, wir hätten einen Satz paralleler Drähte von unendlich Länge, ohne Lampe am Ende. Was würde passieren, wenn wir den Schalter schließen? Da sich am Ende der Drähte keine Last mehr befindet, ist dieser Stromkreis offen. Gäbe es überhaupt keinen Strom? (Abbildung unten)

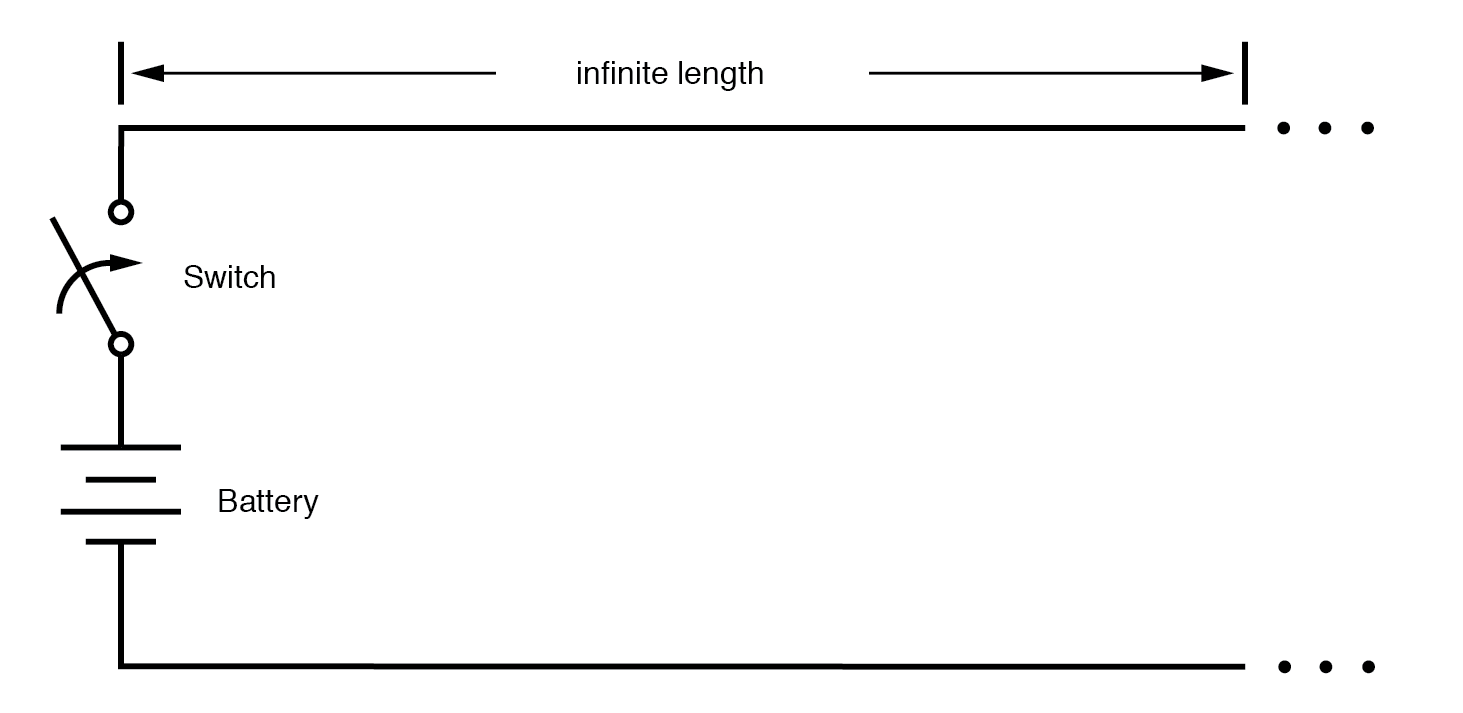
Eine unendliche Übertragungsleitung antreiben.

Obwohl wir in diesem „Gedankenexperiment“ durch den Einsatz von Supraleitern Drahtwiderstände vermeiden konnten, können wir die Kapazitäten entlang der Drähte nicht eliminieren. Alle Durch ein isolierendes Medium getrenntes Leiterpaar erzeugt eine Kapazität zwischen diesen Leitern:(Abbildung unten)

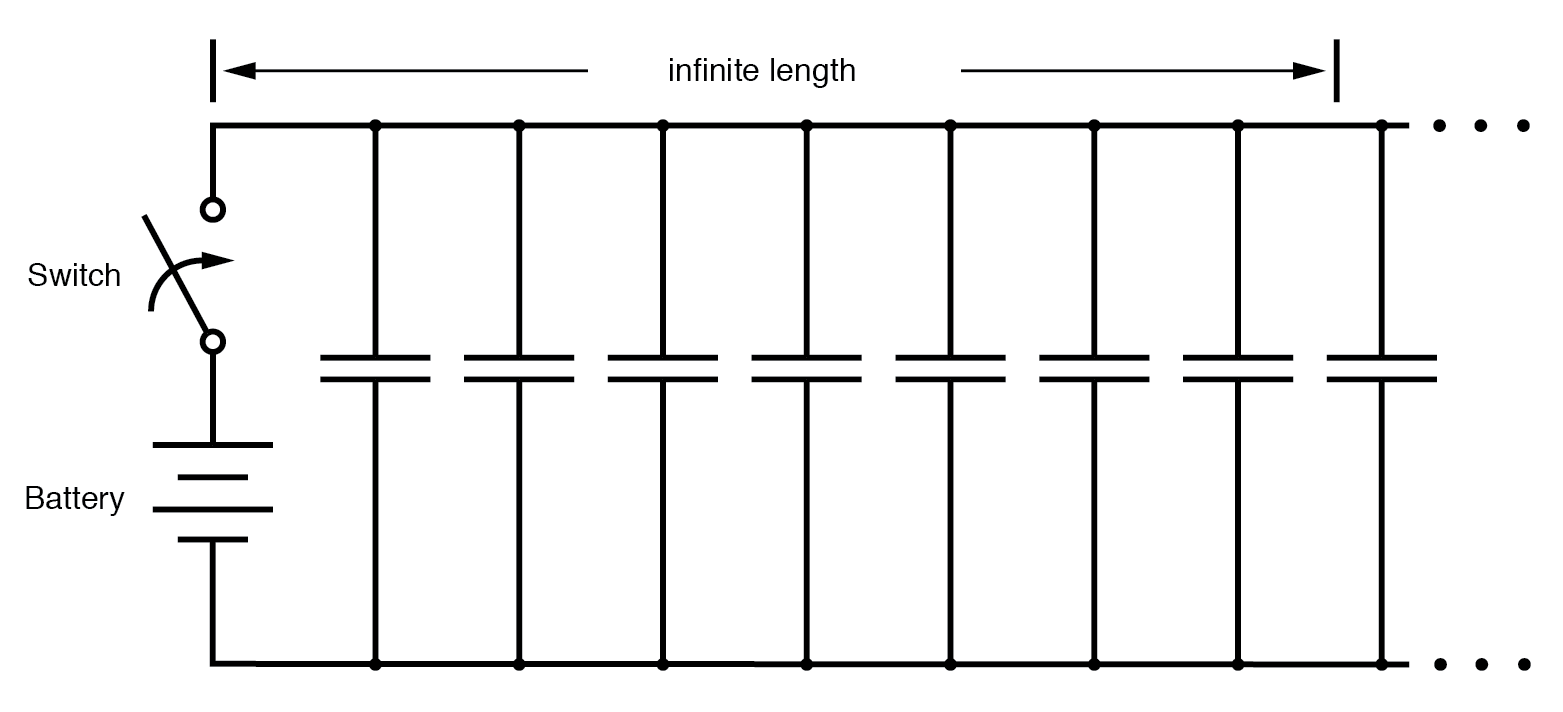
Äquivalenter Schaltkreis, der Streukapazitäten zwischen den Leitern anzeigt.

Zwischen zwei Leitern angelegte Spannung erzeugt ein elektrisches Feld zwischen diesen Leitern. In diesem elektrischen Feld wird Energie gespeichert, und diese Energiespeicherung führt zu einem Widerstand gegen Spannungsänderungen. Die Reaktion einer Kapazität auf Spannungsänderungen wird durch die Gleichung i =C(de/dt) beschrieben, die uns sagt, dass Strom proportional zur zeitlichen Änderungsrate der Spannung gezogen wird. Wenn der Schalter geschlossen ist, reagiert die Kapazität zwischen den Leitern auf den plötzlichen Spannungsanstieg, indem sie sich auflädt und Strom aus der Quelle zieht. Gemäß der Gleichung führt ein sofortiger Anstieg der angelegten Spannung (wie durch perfektes Schließen des Schalters erzeugt) zu einem unendlichen Ladestrom.

Kapazität und Induktivität

Der von einem Paar paralleler Drähte gezogene Strom ist jedoch nicht unendlich, da entlang der Drähte aufgrund der Induktivität eine Reihe von Impedanzen existiert. (Abbildung unten) Denken Sie daran, dass Strom durch beliebige Leiter ein Magnetfeld proportionaler Größe entwickelt. In diesem Magnetfeld wird Energie gespeichert (Abbildung unten) und diese Energiespeicherung führt zu einem Widerstand gegen Stromänderungen. Jeder Draht baut ein magnetisches Feld auf, da er Ladestrom für die Kapazität zwischen den Drähten führt und dabei die Spannung nach der Induktivitätsgleichung e =L(di/dt) abfällt. Dieser Spannungsabfall begrenzt die Spannungsänderungsrate über die verteilte Kapazität und verhindert, dass der Strom jemals eine unendliche Größe erreicht:

Ersatzschaltung mit Streukapazität und -induktivität.

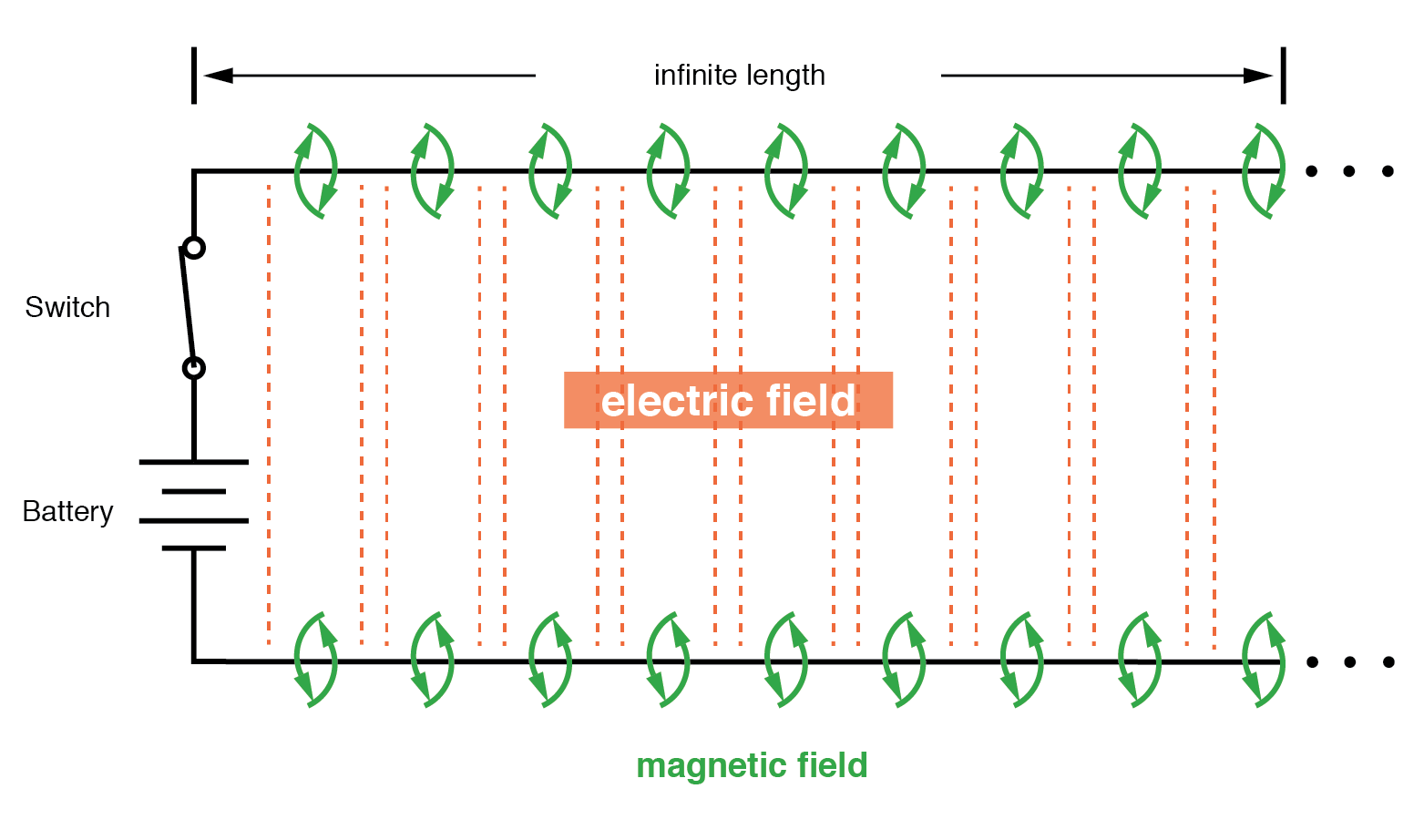
Spannung lädt Kapazität, Strom lädt Induktivität.

Da die elektrischen Ladungsträger in den beiden Drähten die Bewegung mit nahezu Lichtgeschwindigkeit aufeinander zu- und voneinander übertragen, breitet sich die „Wellenfront“ der Spannungs- und Stromänderung mit derselben Geschwindigkeit über die Länge der Drähte aus, was zu der verteilten Kapazität und Induktivität laden sich progressiv auf die volle Spannung bzw. den vollen Strom auf, wie folgt:

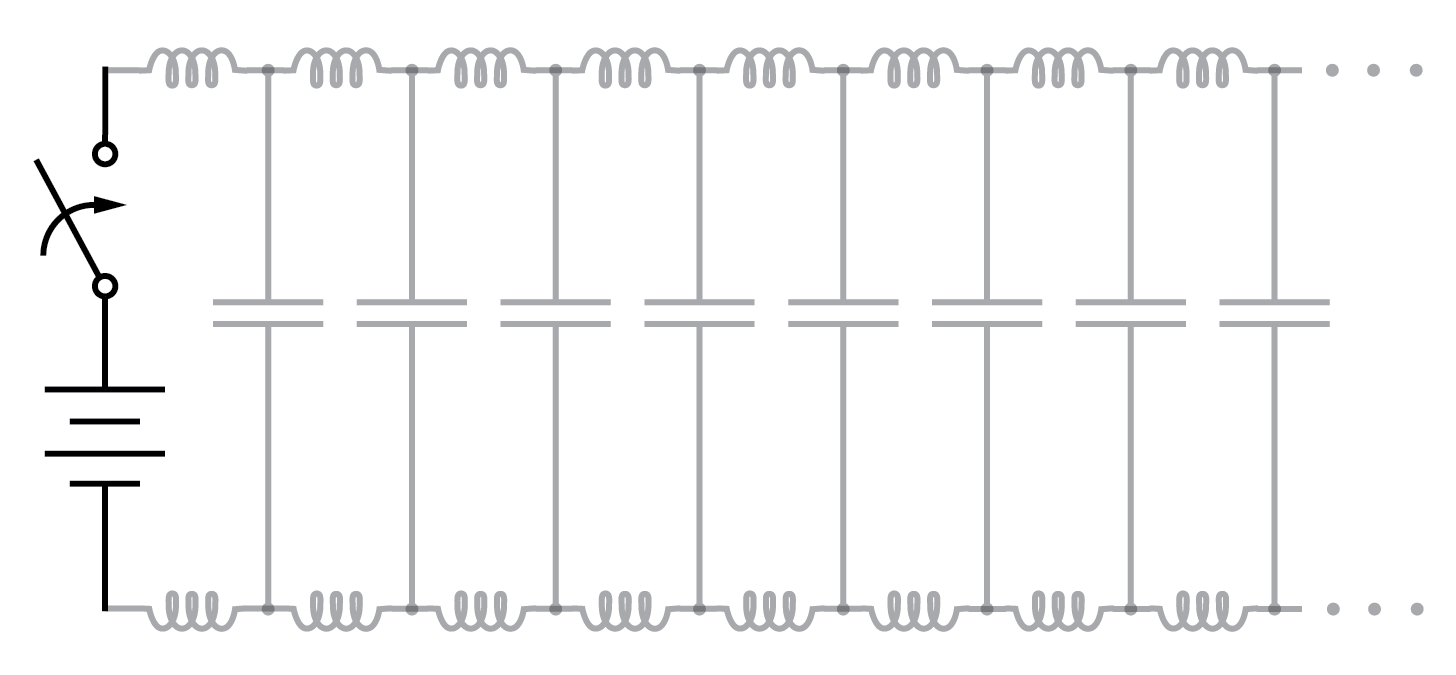
Ungeladene Übertragungsleitung.

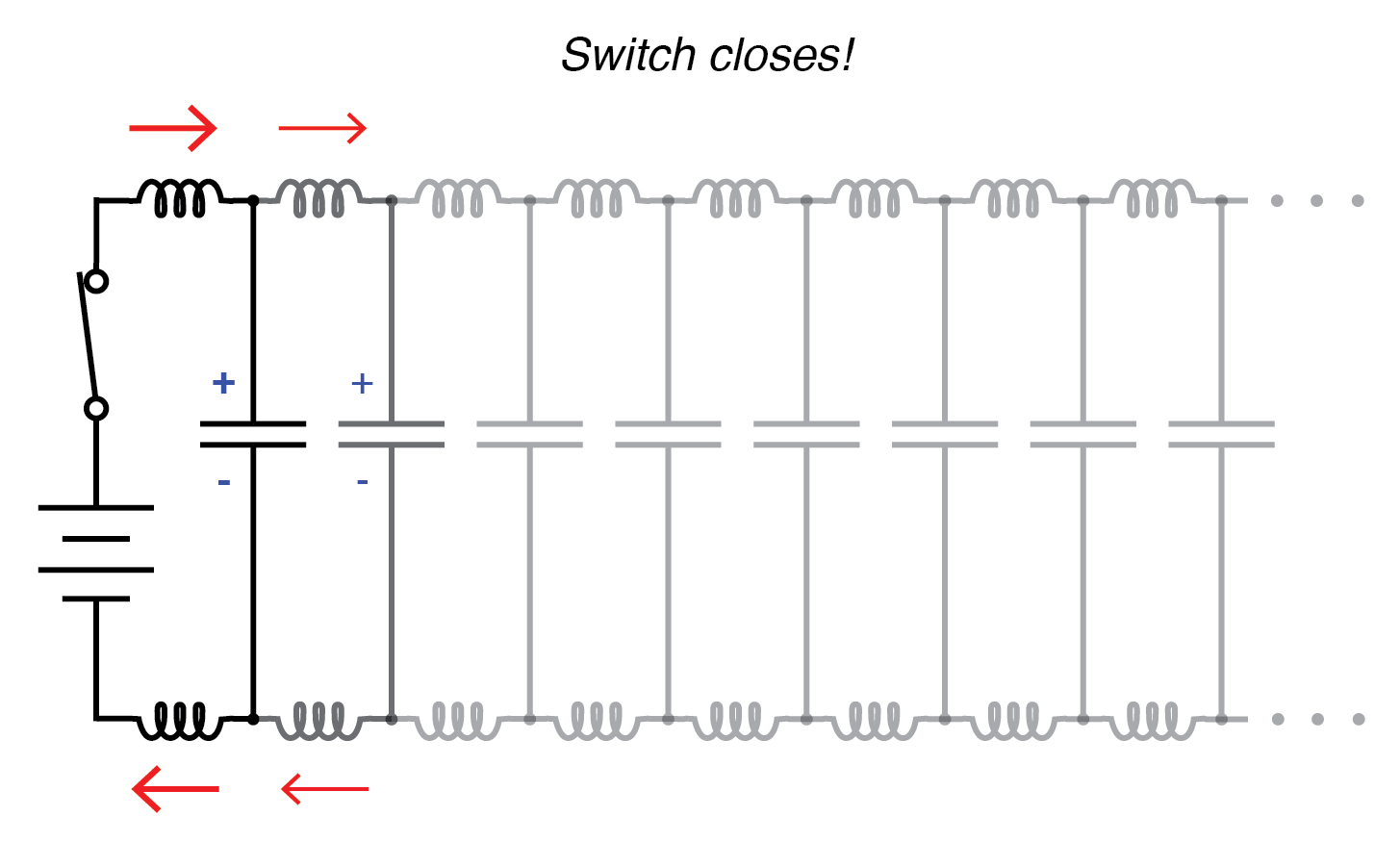
Beginnen Sie mit der Wellenausbreitung.

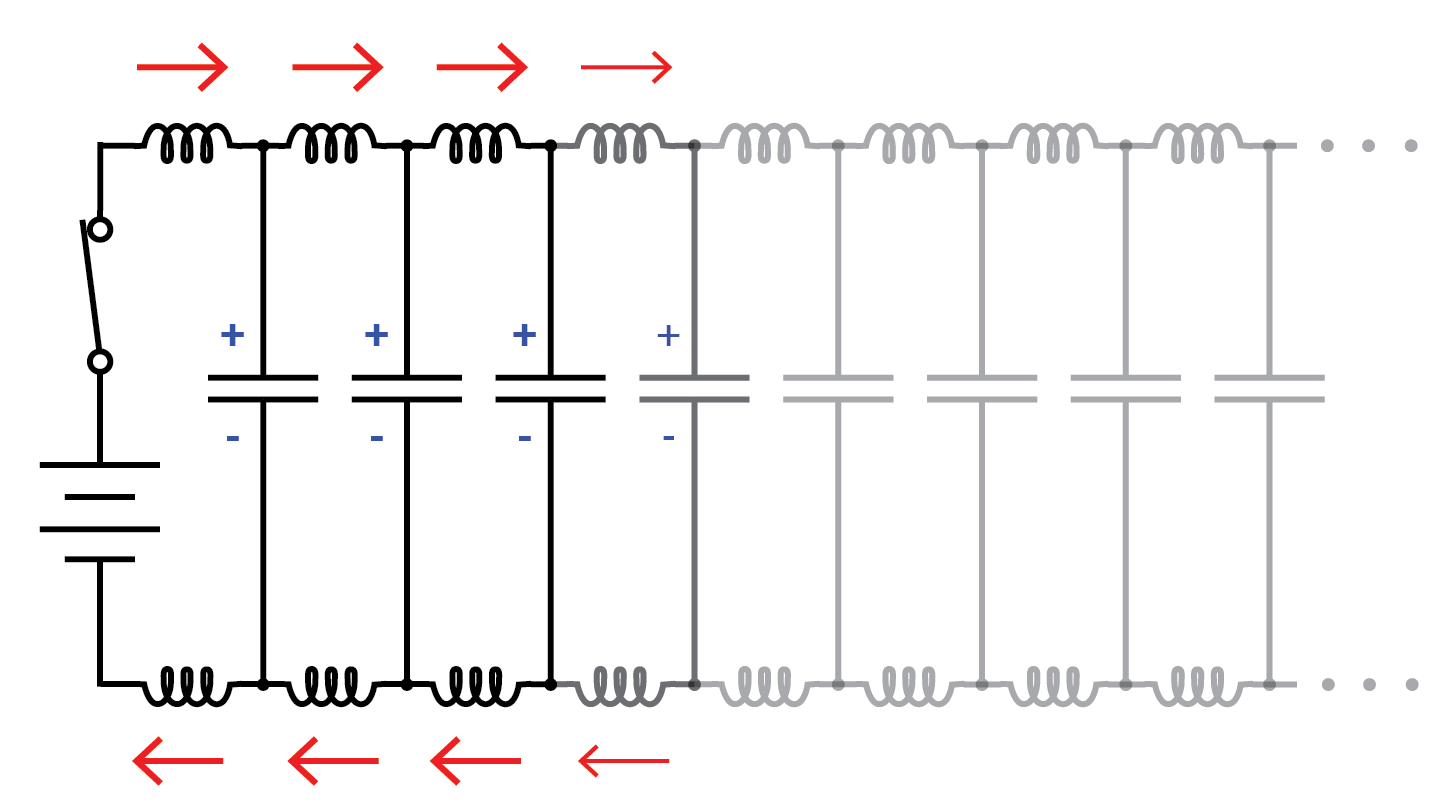
Setzen Sie die Wellenausbreitung fort.

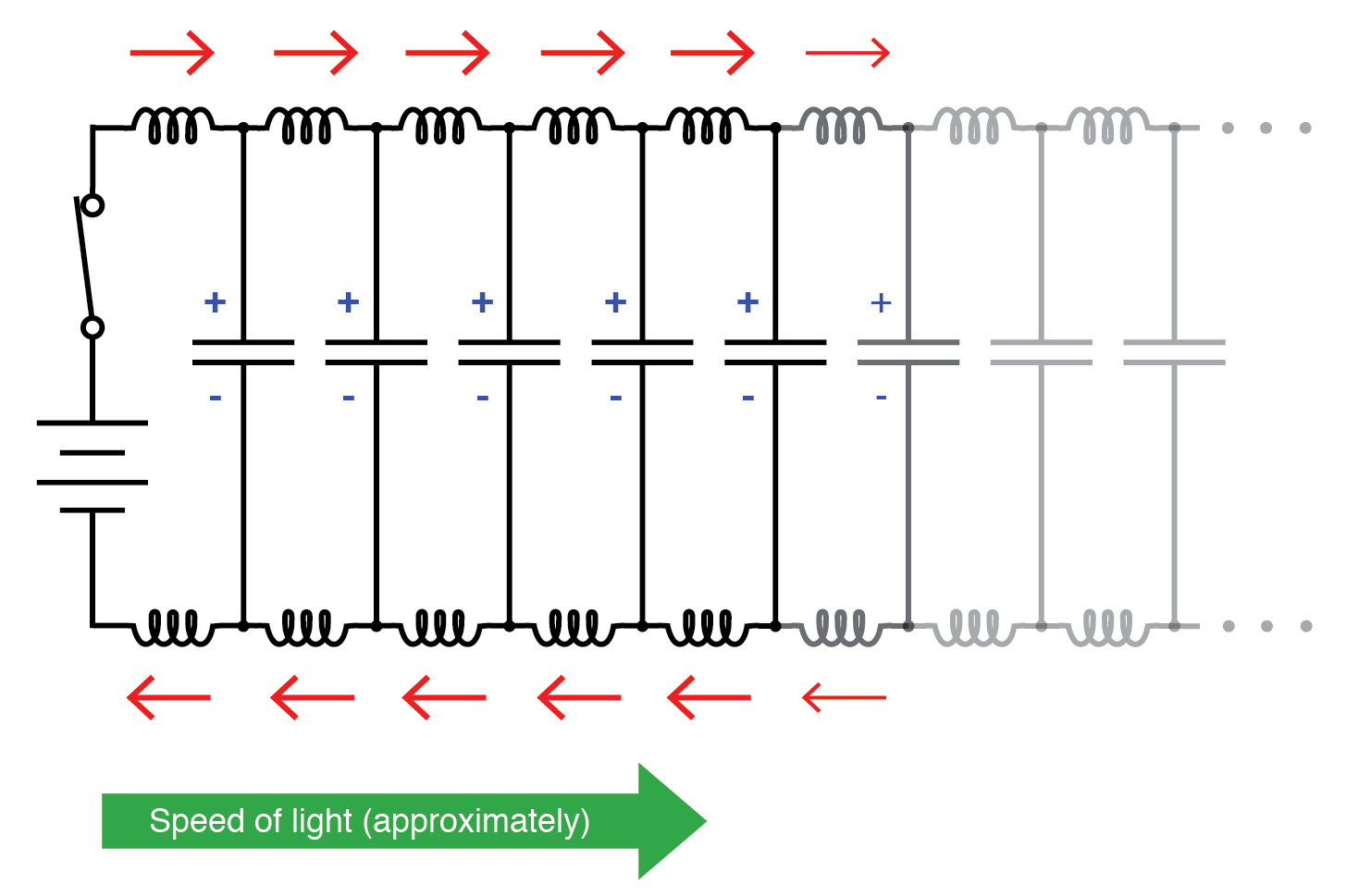
Vermehrt sich mit Lichtgeschwindigkeit.

Die Übertragungsleitung

Das Endergebnis dieser Wechselwirkungen ist ein konstanter Strom begrenzter Größe durch die Batteriequelle. Da die Drähte unendlich lang sind, wird ihre verteilte Kapazität niemals vollständig auf die Quellenspannung aufgeladen und ihre verteilte Induktivität wird niemals einen unbegrenzten Ladestrom ermöglichen. Mit anderen Worten, dieses Kabelpaar zieht Strom von der Quelle, solange der Schalter geschlossen ist, und verhält sich wie eine konstante Last. Die Drähte sind nicht mehr nur Leiter von elektrischem Strom und Träger von Spannungen, sondern bilden nun selbst eine Schaltungskomponente mit einzigartigen Eigenschaften. Die beiden Drähte sind nicht mehr nur ein Leiterpaar , sondern eine Übertragungsleitung .

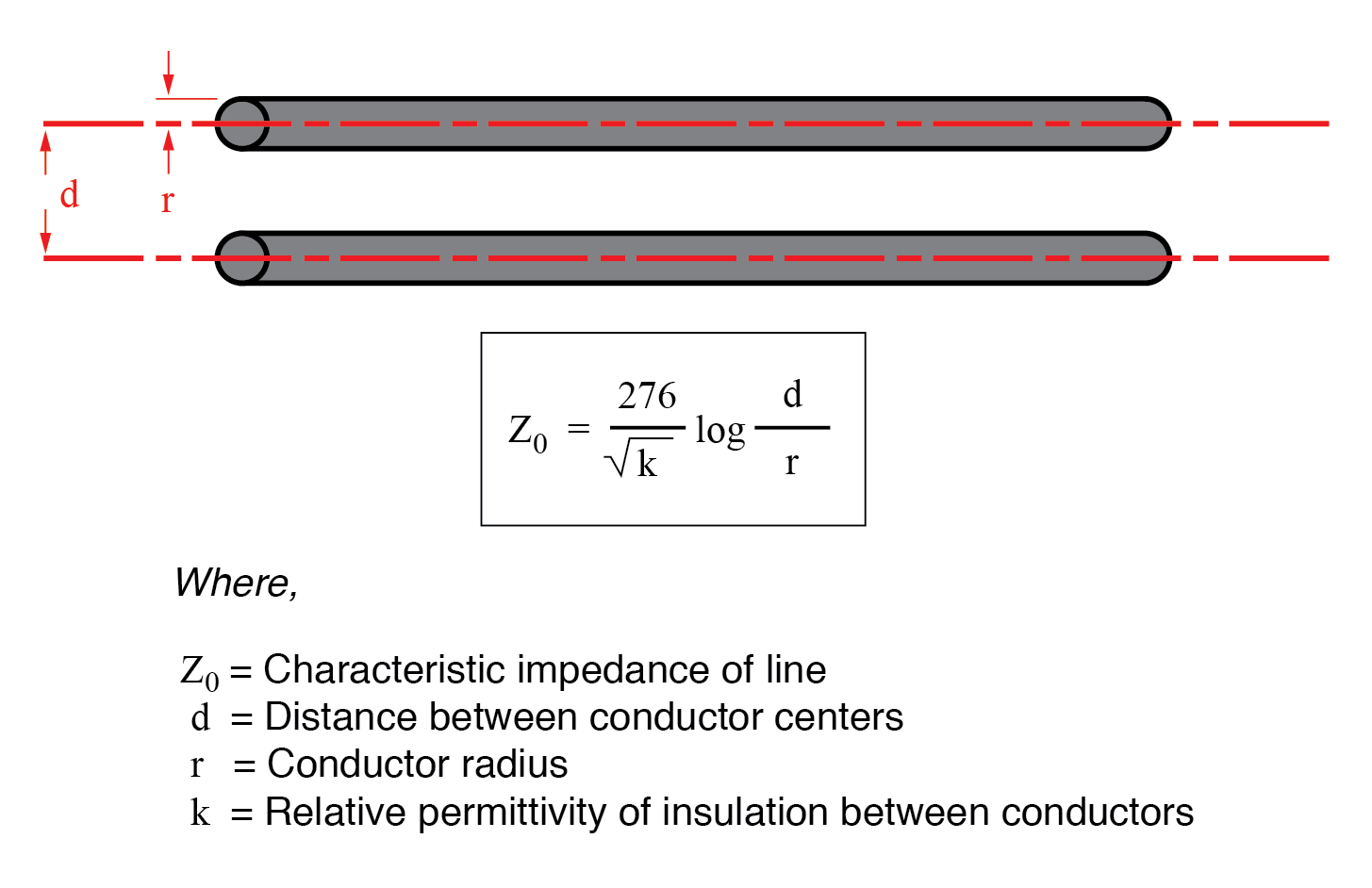
Als konstante Last reagiert die Übertragungsleitung auf die angelegte Spannung eher ohmsch als reaktiv, obwohl sie nur aus Induktivität und Kapazität besteht (unter der Annahme, dass supraleitende Drähte ohne Widerstand sind). Wir können dies sagen, weil es aus Sicht der Batterie keinen Unterschied zwischen einem Widerstand, der ewig Energie abgibt, und einer unendlichen Übertragungsleitung gibt, die ewig Energie absorbiert. Die Impedanz (Widerstand) dieser Leitung in Ohm wird als charakteristische Impedanz bezeichnet , und wird durch die Geometrie der beiden Leiter festgelegt. Für eine paralleladrige Leitung mit Luftisolierung kann der Wellenwiderstand wie folgt berechnet werden:

Wenn die Übertragungsleitung koaxial aufgebaut ist, folgt der Wellenwiderstand einer anderen Gleichung:

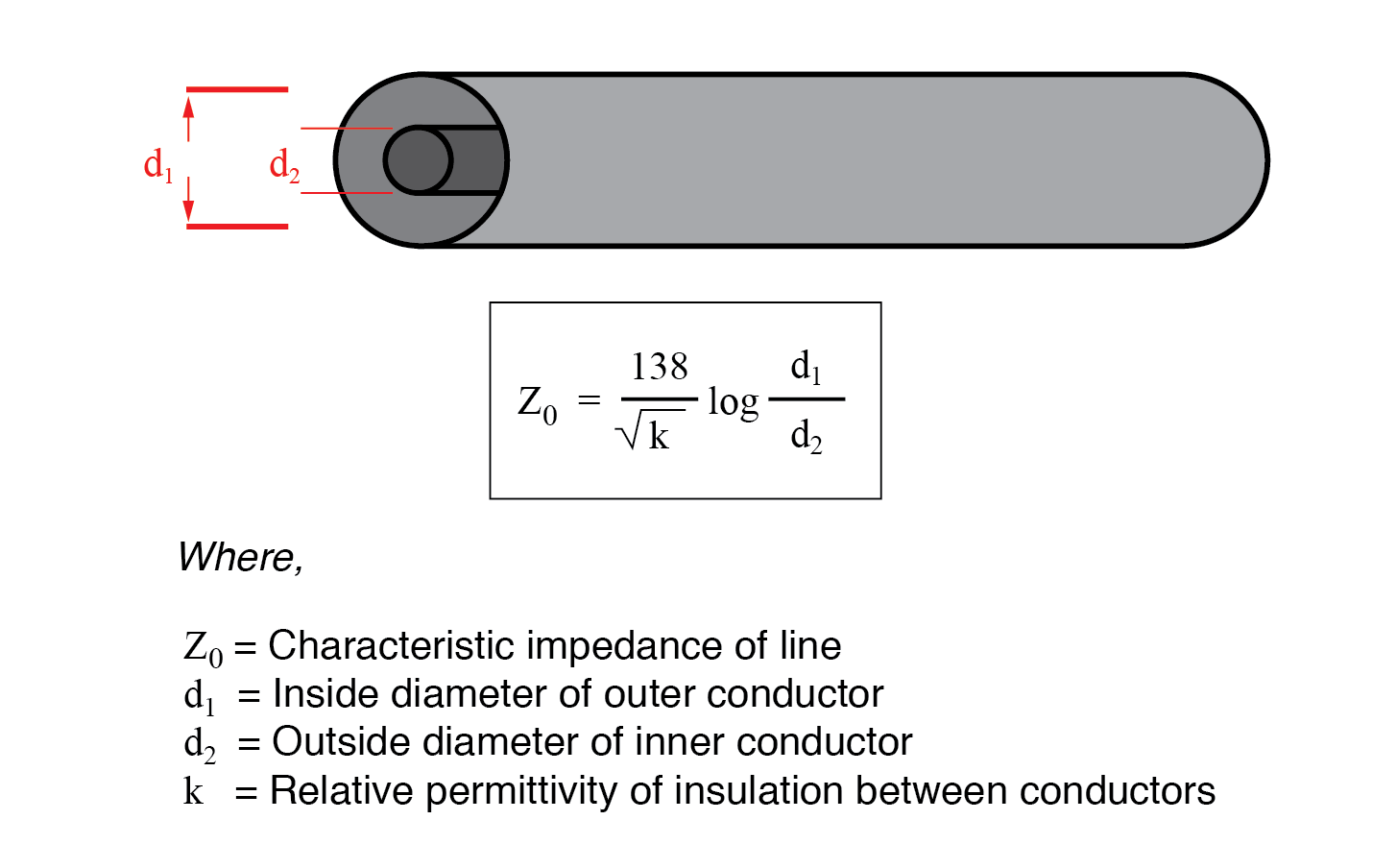
In beiden Gleichungen müssen in beiden Anteilen des Bruchs identische Maßeinheiten verwendet werden. Wenn das Isoliermaterial kein Luft (oder Vakuum) ist, werden sowohl die charakteristische Impedanz als auch die Ausbreitungsgeschwindigkeit beeinflusst. Das Verhältnis der wahren Ausbreitungsgeschwindigkeit einer Übertragungsleitung zur Lichtgeschwindigkeit im Vakuum wird als Geschwindigkeitsfaktor bezeichnet dieser Linie.

Der Geschwindigkeitsfaktor ist ein reiner Faktor der relativen Permittivität des Isoliermaterials (auch bekannt als seine Dielektrizitätskonstante ), definiert als das Verhältnis der elektrischen Feldpermittivität eines Materials zu der eines reinen Vakuums. Der Geschwindigkeitsfaktor jedes Kabeltyps – koaxial oder anderweitig – kann ganz einfach nach der folgenden Formel berechnet werden:

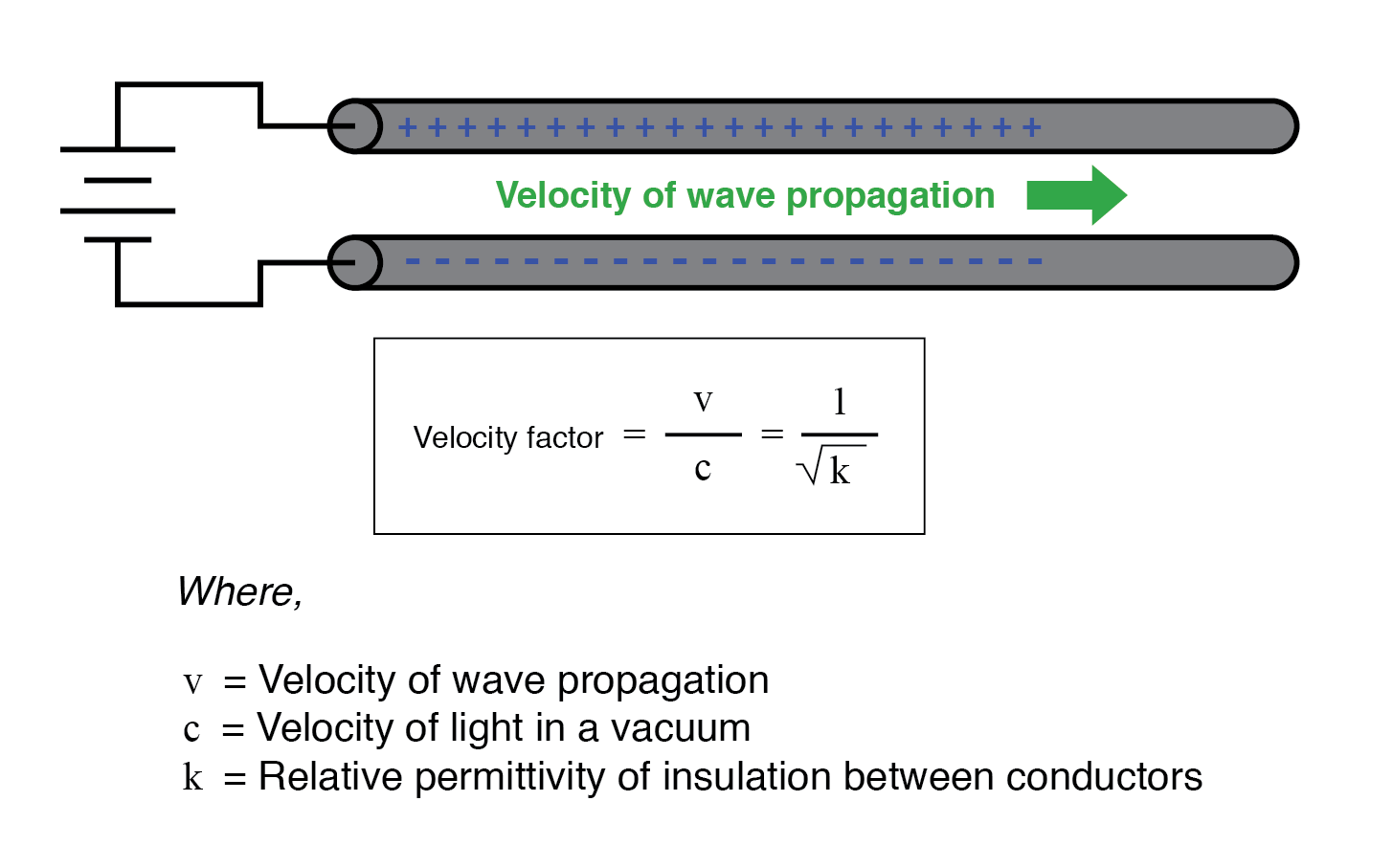
Die natürliche Impedanz

Die charakteristische Impedanz wird auch als natürliche Impedanz bezeichnet , und bezieht sich auf den äquivalenten Widerstand einer Übertragungsleitung, wenn sie unendlich lang wäre, aufgrund der verteilten Kapazität und Induktivität, wenn sich die Spannungs- und Strom-„Wellen“ entlang ihrer Länge mit einer Ausbreitungsgeschwindigkeit ausbreiten, die einem großen Bruchteil der Lichtgeschwindigkeit entspricht.

Aus jeder der ersten beiden Gleichungen ist ersichtlich, dass die charakteristische Impedanz einer Übertragungsleitung (Z₀ ) nimmt mit zunehmendem Leiterabstand zu. Wenn die Leiter voneinander entfernt werden, nimmt die verteilte Kapazität ab (größerer Abstand zwischen den Kondensatorplatten) und die verteilte Induktivität wird größer (weniger Aufhebung der beiden entgegengesetzten Magnetfelder). Weniger Parallelkapazität und mehr Serieninduktivität führen zu einem geringeren Strom, der von der Leitung für jede gegebene angelegte Spannung gezogen wird, was per Definition eine größere Impedanz ist. Umgekehrt erhöht das Annähern der beiden Leiter die Parallelkapazität und verringert die Serieninduktivität. Beide Änderungen führen zu einer größeren Stromaufnahme bei einer gegebenen angelegten Spannung, was einer geringeren Impedanz gleichkommt.

Abgesehen von dissipativen Effekten wie dielektrischer „Leckage“ und Leiterwiderstand ist die charakteristische Impedanz einer Übertragungsleitung gleich der Quadratwurzel des Verhältnisses der Leitungsinduktivität pro Längeneinheit geteilt durch die Leitungskapazität pro Längeneinheit:

RÜCKBLICK:

• Eine Übertragungsleitung ist ein Paar paralleler Leiter, die aufgrund der verteilten Kapazität und Induktivität entlang ihrer Länge bestimmte Eigenschaften aufweisen.
• Wenn an einem Ende einer Übertragungsleitung plötzlich eine Spannung angelegt wird, breiten sich sowohl eine Spannungs-„Welle“ als auch eine Strom-„Welle“ mit nahezu Lichtgeschwindigkeit entlang der Leitung aus.
• Wenn an einem Ende einer unendlich langen Übertragungsleitung eine Gleichspannung angelegt wird, zieht die Leitung Strom von der Gleichstromquelle, als ob sie ein konstanter Widerstand wäre.
• Die charakteristische Impedanz (Z₀ ) einer Übertragungsleitung ist der Widerstand, den sie aufweisen würde, wenn sie unendlich lang wäre. Dies unterscheidet sich vollständig vom Leckwiderstand des Dielektrikums, das die beiden Leiter trennt, und dem metallischen Widerstand der Drähte selbst. Die charakteristische Impedanz ist eine reine Funktion der über die Länge der Leitung verteilten Kapazität und Induktivität und würde selbst dann existieren, wenn das Dielektrikum perfekt wäre (unendlicher Parallelwiderstand) und die Drähte supraleitend (Null-Reihenwiderstand) wären.
• Geschwindigkeitsfaktor ist ein Bruchwert, der sich auf die Ausbreitungsgeschwindigkeit einer Übertragungsleitung zur Lichtgeschwindigkeit im Vakuum bezieht. Für typische Zweidrahtleitungen und Koaxialkabel liegen die Werte zwischen 0,66 und 0,80. Für jeden Kabeltyp ist er gleich dem Kehrwert (1/x) der Quadratwurzel der relativen Permittivität der Kabelisolierung.

VERWANDTE ARBEITSBLÄTTER:

• Arbeitsblatt zur charakteristischen Impedanz