Best Practices für Toleranzstapelung

Toleranzstapelung, auch bekannt als Toleranzstapelung, bezieht sich auf die Kombination verschiedener Teilabmessungstoleranzen. Nachdem eine Toleranz für die Abmessung eines Teils identifiziert wurde , ist es wichtig zu testen, ob diese Toleranz mit den Werkzeugen funktioniert Toleranzen:entweder das obere Ende oder das untere Ende. Ein Teil oder eine Baugruppe kann Ungenauigkeiten unterliegen, wenn seine Toleranzen falsch gestapelt werden.

Die Bedeutung von Toleranzen

Toleranzen wirken sich direkt auf die Kosten und Leistung eines Produkts aus. Engere Toleranzen machen die Herstellung eines bearbeiteten Teils schwieriger und daher oft teurer. Vor diesem Hintergrund ist es wichtig, ein Gleichgewicht zwischen der Herstellbarkeit des Teils, seiner Funktionalität und seinen Kosten zu finden.

Tipps für erfolgreiches Tolerance Stacking

Vermeiden Sie die Verwendung unnötig kleiner Toleranzen

Wie oben erwähnt, führen engere Toleranzen zu höheren Herstellungskosten, da das Teil schwieriger herzustellen ist. Diese höheren Kosten sind häufig auf die erhöhte Menge an verschrotteten Teilen zurückzuführen, die auftreten können, wenn festgestellt wird, dass Abmessungen außerhalb der Toleranz liegen. Die Kosten für hochwertige Werkzeughalter und Werkzeuge mit engeren Toleranzen können ebenfalls zu zusätzlichen Kosten führen.

Darüber hinaus führen unnötig kleine Toleranzen zu längeren Fertigungszeiten, da mehr Arbeit darauf verwendet wird, sicherzustellen, dass das Teil während der Bearbeitung und nach der Bearbeitung im Inspektionsprozess strenge Kriterien erfüllt.

Achten Sie darauf, ein Teil nicht zu überdimensionieren

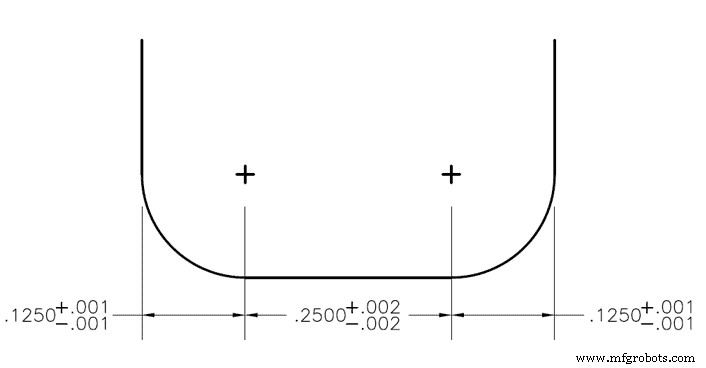
Wenn auf jedem Merkmal eines Teils eine obere und untere Toleranz angegeben ist, kann eine Überdimensionierung zu einem Problem werden. Beispielsweise kann ein Eckenradius-Schaftfräser mit einem rechten und einem linken Eckenradius eine Toleranz von +/- 0,001 Zoll haben, und die Fläche zwischen ihnen hat eine Toleranz von 0,002 Zoll. In diesem Fall würde das Toleranzfenster für den Fräserdurchmesser +/- 0,004 Zoll betragen, wird jedoch bei der Bauteilbemessung häufig falsch berechnet. Darüber hinaus würde das Platzieren einer Toleranz auf diesem Callout dazu führen, dass es überdimensioniert wird, und daher muss das Referenzmaß „REF“ belassen werden, um den Platz der Toleranz einzunehmen.

Statistische Toleranzanalyse verwenden:

Die statistische Analyse betrachtet die Wahrscheinlichkeit, dass alle drei Toleranzen unter oder über der bemessenen Schlitzbreite liegen würden, basierend auf einer Standardabweichung. Diese Wahrscheinlichkeit wird durch eine normale Wahrscheinlichkeitsdichtefunktion dargestellt, die in Abbildung 2 unten zu sehen ist. Durch Kombinieren aller Wahrscheinlichkeiten der verschiedenen Teile und Abmessungen in einem Design können wir die Wahrscheinlichkeit bestimmen, dass ein Teil ein Problem hat oder ganz ausfällt, basierend auf den Abmessungen und Toleranzen der Teile. Im Allgemeinen wird diese Analysemethode nur für Baugruppen mit vier oder mehr Toleranzen verwendet.

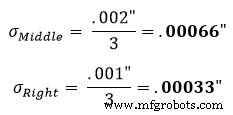
Bevor Sie eine statistische Toleranzanalyse starten, müssen Sie einen Toleranzverteilungsfaktor berechnen oder auswählen. Die Standardverteilung ist 3 . Das bedeutet, dass die meisten Daten (oder in diesem Fall Toleranzen) innerhalb von 3 Standardabweichungen vom Mittelwert liegen. Die Standardabweichungen aller Toleranzen müssen durch diesen Toleranzverteilungsfaktor dividiert werden, um sie von einer Verteilung von 3 auf eine Verteilung von 1 zu normalisieren. Sobald dies geschehen ist, kann die Quadratsumme genommen werden, um die Standardabweichung der Baugruppe zu ermitteln.

Stellen Sie es sich wie eine Tasse Kaffee vor, die mit 3 Bohnen unterschiedlicher Größe zubereitet wird. Um eine köstliche Tasse Kaffee zuzubereiten, müssen Sie zuerst alle Bohnen auf die gleiche Größe mahlen, damit sie in den Kaffeefilter gegeben werden können. In diesem Fall sind die Bohnen die Standardabweichungen, die Mühle der Toleranzverteilungsfaktor und der Kaffeefilter die Quadratsummengleichung. Dies ist notwendig, da einige Toleranzen je nach Enge des Toleranzbereichs unterschiedliche Verteilungsfaktoren haben können.

Die statistische Analysemethode wird verwendet, wenn die Anforderung besteht, dass der Schlitz 0,500 Zoll breit sein muss mit einer Toleranz von +/- 0,003 Zoll, die Radien (0,125 Zoll) und die Abflachung (0,250 Zoll) jedoch nicht erforderlich sind. ), um genau zu sein, solange sie in den Schlitz passen. In diesem Beispiel haben wir 3 bilaterale Toleranzen mit ihren Standardabweichungen bereits verfügbar. Da sie bilateral sind, wäre die Standardabweichung vom Mittelwert einfach gleich dem + oder – Toleranzwert. Für die Außenradien wäre dies 0,001 Zoll und für den mittleren flachen Bereich 0,002 Zoll.

Lassen Sie uns für dieses Beispiel die Standardabweichung (σ) jedes Abschnitts mithilfe von Gleichung 1 ermitteln. In dieser Gleichung steht die Standardabweichung.

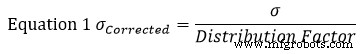
Die Standardannahme ist, dass eine Teiletoleranz eine +/- 3-Normalverteilung darstellt. Daher ist der Verteilungsfaktor 3. Unter Verwendung von Gleichung 1 im linken Abschnitt von Abbildung 1 finden wir heraus, dass seine korrigierte Standardabweichung entspricht:

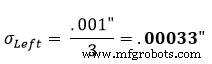
Dies wird dann für den mittleren und rechten Abschnitt wiederholt:

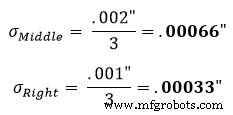
Nachdem wir diese Standardabweichungen erhalten haben, geben wir die Ergebnisse in Gleichung 2 ein, um die Standardabweichung der Toleranzzone zu finden. Gleichung 2 ist bekannt als Wurzel-Summe-Quadrat-Gleichung.

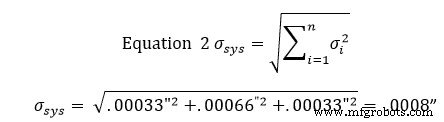
An diesem Punkt bedeutet dies, dass 68 % der Slots innerhalb einer Toleranz von +/- 0,0008 Zoll liegen. Die Multiplikation dieser Toleranz mit 2 ergibt ein Konfidenzfenster von 95 %, während die Multiplikation mit 3 ein Konfidenzfenster von 99 % ergibt.

68 % der Slots liegen innerhalb von +/- 0,0008 Zoll

95 % der Slots liegen innerhalb von +/- 0,0016 Zoll

99 % der Slots liegen innerhalb von +/- 0,0024 Zoll

Diese Konfidenzfenster sind Standard für einen normalverteilten Satz von Datenpunkten. Eine Standardnormalverteilung ist in Abbildung 2 oben zu sehen.

Die statistische Toleranzanalyse sollte nur für Baugruppen mit mehr als 4 tolerierten Teilen verwendet werden. Viele Faktoren wurden in dieser einfachen Analyse nicht berücksichtigt. Dieses Beispiel galt für 3 bilaterale Dimensionen, deren Toleranzen repräsentativ für ihre Standardabweichungen von ihren Mittelwerten waren. Bei der standardmäßigen statistischen Toleranzanalyse kommen andere Variablen ins Spiel, wie Winkel, Unrundheit und Parallelität, die Korrekturfaktoren erfordern.

Wussten Sie, dass die Marken der Harvey Performance Company mit den führenden Kamerasoftwareanbietern der Branche zusammenarbeiten, um Werkzeugbibliotheken bereitzustellen?

Klicken Sie hier, um mehr zu erfahren

Worst-Case-Analyse verwenden:

Bei der Worst-Case-Analyse werden alle Toleranzen eines Teils addiert, um die Gesamtteiltoleranz zu ermitteln. Bei der Durchführung dieser Art von Analyse wird jede Toleranz auf ihre größte oder kleinste Grenze in ihrem jeweiligen Bereich eingestellt. Diese Gesamttoleranz kann dann mit den Leistungsgrenzen des Teils verglichen werden, um sicherzustellen, dass die Baugruppe richtig konstruiert ist. Dies wird normalerweise für nur 1 Dimension (nur 1 Ebene, daher keine Winkel beteiligt) und für Baugruppen mit einer kleinen Anzahl von Teilen verwendet.

Die Worst-Case-Analyse kann auch bei der Auswahl des geeigneten Schneidwerkzeugs für Ihre Arbeit verwendet werden, da die Werkzeugtoleranz für ein Worst-Case-Szenario zur Teiletoleranz hinzugefügt werden kann. Sobald dieses Szenario identifiziert ist, kann der Maschinist oder Ingenieur die entsprechenden Anpassungen vornehmen, um das Teil innerhalb der auf dem Druck angegebenen Abmessungen zu halten. Dabei ist zu beachten, dass der Worst-Case-Szenario in der realen Produktion selten eintritt. Während diese Analysen für die Fertigung teuer sein können, geben sie den Maschinisten Sicherheit, indem sie garantieren, dass alle Baugruppen ordnungsgemäß funktionieren. Oft erfordert diese Methode enge Toleranzen, da die Gesamtstapelung bei maximalen Bedingungen das primäre Merkmal ist, das bei der Konstruktion verwendet wird. Engere Toleranzen erhöhen die Herstellungskosten aufgrund des erhöhten Schabaufwands, der Produktionszeit für die Inspektion und der Werkzeugkosten für diese Teile.

Beispiel für ein Worst-Case-Szenario im Kontext zu Abbildung 1:

Finden Sie die untere Spezifikationsgrenze.

Für den Radius der linken Ecke

0,125 Zoll – 0,001 Zoll =0,124 Zoll

Für den flachen Abschnitt

0,250 Zoll – 0,002 Zoll =0,248 Zoll

Für den richtigen Eckenradius

0,125 Zoll – 0,001 Zoll =0,124 Zoll

Fügen Sie all dies zur unteren Spezifikationsgrenze hinzu:

0,124 Zoll + 0,248 Zoll + 0,124 Zoll =0,496 Zoll

Finden Sie die obere Spezifikationsgrenze:

Für den Radius der linken Ecke

0,125" + 0,001" =0,126"

Für den flachen Abschnitt

0,250" + 0,002" =0,252"

Für den richtigen Eckenradius

0,125" + 0,001" =0,126"

Fügen Sie all dies zur unteren Spezifikationsgrenze hinzu:

0,126 Zoll + 0,252 Zoll + 0,126 Zoll =0,504 Zoll

Subtrahieren Sie die beiden und teilen Sie dieses Ergebnis durch zwei, um die Worst-Case-Toleranz zu erhalten:

(Obergrenze – Untergrenze)/2 =0,004”

Daher ist das Worst-Case-Szenario dieses Slots 0,500" +/- 0,004".