Ultraschmalbandiger perfekter Absorber und seine Anwendung als plasmonischer Sensor im sichtbaren Bereich

Hintergrund

In den letzten Jahren haben plasmonische Metamaterialien, die auf der lokalisierten Oberflächenplasmonenresonanz (LSPR) basieren, aufgrund ihrer elektromagnetischen Eigenschaften und vielversprechenden Anwendungen wie den Monopolresonatoren erhebliche Fortschritte erzielt [1,2,3,4,5,6,7,8] , die Verbesserung der Lichtdurchlässigkeit [9,10,11,12,13] und die plasmonischen Sensoren [14,15,16,17,18,19,20,21]. Für einen Metamaterial-Absorber ist es vorteilhaft, die Absorption elektromagnetischer Wellen zu verbessern, während die intrinsischen optischen Verluste von Metallen beim Design anderer Geräte sorgfältig berücksichtigt werden müssen. Der erste perfekte Metamaterial-Absorber wird von Landy vorgeschlagen und demonstriert [22]. Danach wurden schnell perfekte Metamaterial-Absorber entwickelt [23,24,25,26,27,28,29,30,31], die nach ihren unterschiedlichen Anwendungsanforderungen allgemein in Schmalbandabsorber und Breitbandabsorber eingeteilt werden können. Im Allgemeinen können die Breitbandabsorber in Energy Harvester verwendet werden, während die Schmalbandabsorber in Sensoren und monochromatischen Photodetektoren verwendet werden.

Bei Sensoranwendungen hat der plasmonische Brechungsindexsensor auf Basis von Schmalbandabsorbern viel Aufmerksamkeit auf sich gezogen. Bis heute wurde über viele verschiedene Typen von plasmonischen Brechungsindexsensoren berichtet, die im Infrarot- und Terahertz-Bereich arbeiten, darunter hybride Mikrokavitäten [32, 33], Nanoscheiben [34], netzwerkartige Metaoberflächen [24], Metallgitter [28] und so weiter [35,36,37]. Beachten Sie, dass im Vergleich zu den plasmonischen Sensoren, die im Infrarot-, Terahertz- und Mikrowellenbereich arbeiten, die im sichtbaren Band arbeitenden Sensoren eine geringere Periodizität der Metamaterialstruktur realisieren können, was die Nutzung dieser Geräte in vielen praktischen Anwendungen wie Chemie und . verbessern kann Biologie [38]. Leider haben die früher veröffentlichten plasmonischen Brechungsindexsensoren im sichtbaren Bereich im Allgemeinen einen vergleichsweise niedrigen FOM, was ihre weitere Entwicklung und Anwendung stark erschwert. In theoretischen Studien haben Zhou et al. schlugen theoretisch einen Brechungsindexsensor im sichtbaren Bereich vor, der die Subwellenlängen-Metallgitterstrukturen mit einem S . verwendet von 300 nm/RIU, aber die FOM beträgt nur 2 [28]. Liuet al. entwarfen einen multispektralen Sensor mit plasmonischen Nanokavitäten tiefer Subwellenlänge und demonstrierten eine FOM von 58 [34]. Mit den Bemühungen von Liu et al. wurde über die plasmonische Struktur mit netzwerkartiger Metaoberfläche ein Brechungsindexsensor mit einer minimalen FWHM von 3 nm und einer FOM von 68,57 erhalten [24]. In experimentellen Studien demonstrierten Emiko und Tetsu 2014 experimentell einen LSPR-Sensor basierend auf einer einzelnen Au-Nanosternstruktur mit einem S von 665 nm/RIU und einer FWHM von bis zu 40 nm [39]. Cho et al. berichteten über eine experimentelle Demonstration eines plasmonischen Brechungsindexsensors mit dem S 378 nm/RIU erreicht [40]. Sowohl theoretisch als auch experimentell haben viele Forscher große Anstrengungen unternommen, um das FOM des im sichtbaren Bereich arbeitenden Brechungsindexsensors zu verbessern. Es ist jedoch immer noch eine große Herausforderung, einen plasmonischen Brechungsindexsensor mit einem hohen FOM im sichtbaren Bereich zu entwickeln, was seine Anwendungen stark einschränkt.

Bei Sensoren ist es sehr sinnvoll, FOM zu erhöhen. Im biologischen Bereich bedeutet beispielsweise ein höherer FOM des Brechungsindexsensors eine stärkere Leistung bei der Moleküldetektion. Die FOM des Sensors in dieser Arbeit kann 233,5 erreichen, was weit höher ist als die des veröffentlichten plasmonischen Brechungsindexsensors im sichtbaren Bereich [24, 28, 34]. Der plasmonische Sensor basiert auf der periodischen Metall-Dielektrikum-Metall (MDM)-Struktur. Dann kann die Struktur auch als perfekter ultraschmalbandiger plasmonischer Absorber mit einer Absorptionseffizienz von über 95 % und einer FWHM von nur 1,82 nm im sichtbaren Bereich arbeiten. Außerdem untersuchen wir den Einfluss von Strukturabmessungen und Materialparametern auf die optischen Eigenschaften des Metamaterials. Darüber hinaus zeigen wir, dass im Vergleich zu den üblichen MDM-Strukturen die Verwendung von dreieckigen Nanobändern in der Struktur hilfreich ist, um die Absorptionsleistung zu verbessern. Und mittlerweile werden auch die Absorptionsmechanismen im Detail untersucht und analysiert. Unter Berücksichtigung der Herstellung der vorgeschlagenen Struktur können die dreieckigen Nanobänder durch viele Methoden hergestellt werden, wie z. B. Elektronenstrahllithographie [41], Formen [42] und Imprint-Lithographie [43]. Es wird erwartet, dass unsere Arbeit eine Anleitung für das Design eines plasmonischen Sensors sein wird.

Methoden

Abbildung 1 veranschaulicht den Querschnitt einer Elementarzelle für die vorgeschlagene Metamaterialstruktur. Die Struktur besteht aus zwei Gold-Nanobändern auf einer dünnen Goldschicht, die zwischen der dielektrischen Schicht und dem Substrat angeordnet ist, und zwischen den Gold-Nanobändern befindet sich ein dreieckiges Gold-Nanoband. In unserer Simulation wird die Permittivität von Gold durch das Drude-Modell charakterisiert. Das Dielektrikum der Mittelschicht und des Substrats werden als NaF (n = 1.3) und MgF₂ (n = 1.4) bzw. Wir verwenden die zweidimensionale Finite-Difference-Time-Domain-(FDTD)-Methode, um die Transmission und Reflexion der vorgeschlagenen Struktur zu berechnen, und die Absorption der gesamten Struktur wird als A . definiert = 1 − R − T. Wir stellen periodische Randbedingungen in x-Richtung ein, und die transversale magnetische (TM) Welle fällt normal auf die Struktur mit Polarisation entlang der x-Richtung.

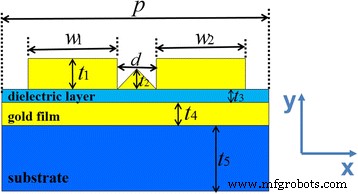
Schema der vorgeschlagenen Metamaterialstruktur einer Elementarzelle

Wie wir alle wissen, wird das LC-Ersatzschaltungsmodell häufig verwendet, um die durch LSPR angeregte Magnetresonanz für einen perfekten Absorber qualitativ vorherzusagen [44,45,46]. Zur Vereinfachung der Diskussion über das LC-Modell ist das Schema der Metamaterial-Absorberstruktur in Abb. 2a dargestellt. Und das äquivalente LC-Modell ist in Abb. 2b gezeigt. Hier kann die Lückenkapazität zwischen den Nanobändern in benachbarten Einheiten als C . ausgedrückt werden _g = ε ₀ t ₁ /(P − d − 2w ), wobei ε ₀ ist die dielektrische Permittivität der Umgebung. Die Kapazität C _m = c ₁ ε ₃ ε ₀ (2w + d )/t ₃ wird verwendet, um die Kapazität zwischen den Nanobändern und dem Goldfilm darzustellen, wobei c ₁ ist ein Koeffizient aufgrund der ungleichmäßigen Ladungsverteilung auf der Metalloberfläche und ε ₃ die Permittivität der dielektrischen Schicht ist [44,45,46]. Die Gegeninduktivität der Goldnanobänder und des Goldfilms ist gegeben durch L _m = 0.5μ ₀ (2w + d )t ₃ , wobei μ ₀ ist die Durchlässigkeit der Umgebung. Um den Beitrag der Driftladungen in den Goldnanobändern und dem Goldfilm zu berücksichtigen, ist die kinetische Induktivität gegeben durch \({L}_e=\left(2w+d\right)/\left(\gamma {\varepsilon} _0{t}_1{\omega}_p^2\right) \), wobei γ ist ein Koeffizient, der für die effektive Querschnittsfläche der Gold-Nanobänder und ω _p ist die Plasmafrequenz des Goldes [44,45,46]. Dann kann die Gesamtimpedanz für das äquivalente LC-Schaltungsmodell ausgedrückt werden als

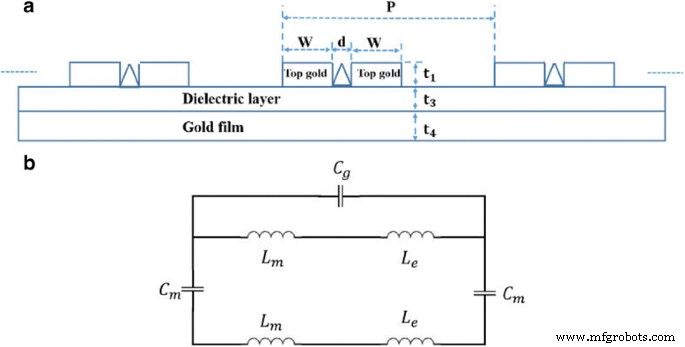
a Schema der Metamaterial-Absorberstruktur. b Schema des äquivalenten LC-Schaltungsmodells für die Struktur von Fig. 6a

Die Resonanzwellenlänge kann erhalten werden, wenn Z _tnicht = 0.

Die Kopplung zwischen den Nanobändern in benachbarten Einheiten ist aufgrund der großen Lücke (P − d − 2w ) zwischen den Nanobändern. Der Einfluss von C _g kann ignoriert werden, wenn C _g weniger als 5 % von C . beträgt _m . Somit kann in dieser Situation die Resonanzwellenlänge vereinfacht werden auf

wo L _m = 0.5μ ₀ (2w + d )t ₃ , \( {L}_e=\left(2w+d\right)/\left(\gamma {\varepsilon}_0{t}_1{\omega}_p^2\right)\), und C _m = c ₁ ε ₃ ε ₀ (2w + d )/t ₃ . Im LC-Schaltungsmodell lassen sich die Einflüsse der Strukturdimensionen auf die Resonanzwellenlänge durch Gl. (3). Es ist leicht zu beobachten, dass die Resonanzwellenlänge λ _r würde mit größerer Permittivität zunehmen (ε ₃ ) der dielektrischen Schicht aufgrund der Zunahme von C _m . Ebenso die größere Breite w führt zu den größeren Werten für L _m , L _e , und C _m , was zu einer Rotverschiebung der Resonanzwellenlänge führt. Die Zunahme der Permittivität (ε ₀ ) der Umgebung führt zu einem größeren L _m C _m Werte, während der andere Begriff L _e C _m ist unabhängig vom ε ₀ in Gl. (3). Somit nimmt die Resonanzwellenlänge mit der Zunahme von ε . zu ₀ .

Ergebnisse und Diskussion

Dann beginnen wir die Diskussion mit den folgenden Strukturdimensionen. Die Struktur hat eine Gitterperiode von P = 580 nm in x-Richtung. Die Höhen des quadratischen Gold-Nanobands und des dreieckigen Gold-Nanobands sind jeweils als t . festgelegt ₁ = 45 nm und t ₂ = 30 nm . Die Dicke der dielektrischen Schicht, des Goldfilms und des Substrats beträgt t ₃ = 10 nm, t ₄ = 25 nm , und t ₅ = 165 nm , bzw. Die Breite des dreieckigen Gold-Nanobands und des quadratischen Gold-Nanobands beträgt d = 75 nm und w ₁ = w ₂ = w = 142nm , bzw. Abbildung 3a zeigt die simulierten Absorptions-, Reflexions- und Transmissionsspektren der entworfenen Struktur. Wie in Abb. 3a gezeigt, kann die Absorptionseffizienz bis zu 95 % erreichen, und der Reflexionsabfall der Struktur unter 0,001 wird bei 751,225 nm gefunden. Die FWHM beträgt 1,82 nm, was viel schmaler ist als die des zuvor berichteten Schmalbandabsorbers im sichtbaren Bereich [24, 28, 34, 39].

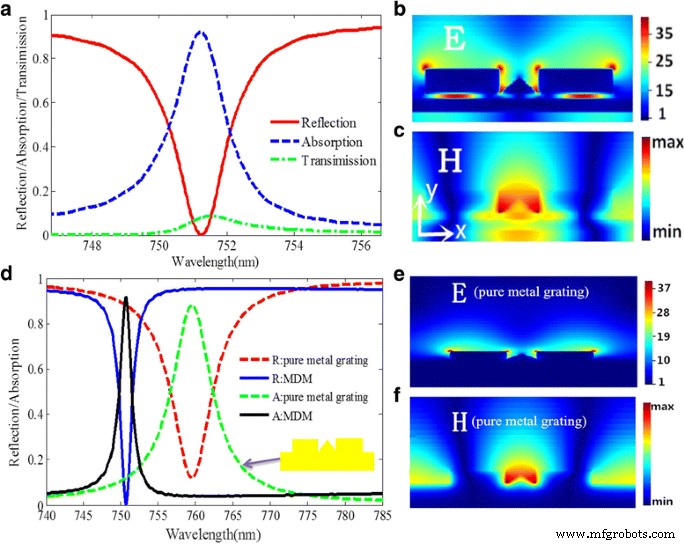
a Absorptions-, Reflexions- und Transmissionsspektren der vorgeschlagenen Struktur. b Verteilungen des elektrischen Feldes E der MDM-Struktur bei Resonanzspitze. c Verteilungen des magnetischen Feldes H der MDM-Struktur bei Resonanzspitze. d Die Reflexions- und Absorptionsspektren der MDM-Struktur und der reinen Metallgitterstruktur. e Verteilungen des elektrischen Feldes E der reinen Metallgitterstruktur am Resonanzpeak. f Verteilungen des magnetischen Feldes H der reinen Metallgitterstruktur am Resonanzpeak

Um den physikalischen Mechanismus des Absorptionspeaks auszuarbeiten, werden die Verteilungen des elektrischen Felds E und des magnetischen Felds H am Resonanzpeak berechnet und in Abb. 3b, c dargestellt. Wie in Fig. 3b gezeigt, kann die Amplitude des elektrischen Felds in den Lücken eindeutig einen Wert erreichen, der bis zu 35 mal größer ist als der des einfallenden Lichts. Daher kann die vorgeschlagene Struktur nicht nur die perfekte Absorption, sondern auch die Verstärkung des elektrischen Felds in einem Nanospalt realisieren, was ein wichtiges Phänomen bei Biosensoranwendungen ist. Wie in Abb. 3c gezeigt, ist das stärkste Magnetfeld im Raum zwischen zwei Gold-Nanobändern konzentriert und dringt etwas in die dielektrische Schicht ein, was auf den Kopplungseffekt hindeutet, der aus der LSPR resultiert. Um den Einfluss der dielektrischen Schicht und des Goldfilms auf die ultraschmale FWHM und die hohe Absorptionsleistung weiter zu verstehen, werden dann das Absorptions- und Reflexionsspektrum analysiert und zwischen der MDM-Struktur und der reinen Metallgitterstruktur mit derselben verglichen Dimensionsparameter, wie in Abb. 3d gezeigt. Offensichtlich hat die MDM-Struktur eine schmalere FWHM und eine geringere Reflektivität des Resonanzeinbruchs. Das elektrische Feld und das magnetische Feld der Metallgitterstruktur werden simuliert und in Abb. 3e bzw. f dargestellt. Verglichen mit der Magnetfeldverteilung der MDM-Struktur befindet sich das Magnetfeld der Metallgitterstruktur offensichtlich nur auf der Oberfläche des dreieckigen Gold-Nanobandes, ohne dass das Magnetfeld das Metall durchdringt, was verwendet werden kann, um das Vergleichsergebnis von . zu erklären die Absorption zwischen der MDM-Struktur und der Metallgitterstruktur. Darüber hinaus ist die elektrische Feldstärke zwischen zwei Gold-Nanobändern und dem dünnen Goldfilm aufgrund des Kopplungsverhaltens in der Struktur, wie in Abb. 3b gezeigt, etwa 40-mal größer als die der einfallenden Wellen, was viel größer ist als angegeben in ref. [25].

Abbildung 4a zeigt die Auswirkung der Polarisationskonfiguration des einfallenden Lichts auf das Absorptionsspektrum des vorgeschlagenen Metamaterial-Absorbers. Es ist ersichtlich, dass die Struktur in der TM-Konfiguration einen scharfen Absorptionspeak aufweist, jedoch nicht in der TE-Konfiguration. Offensichtlich kann die LSPR bei TE-Konfiguration nicht durch das einfallende Licht angeregt werden, was durch die asymmetrische Struktur des Absorbers gut erklärt werden kann. Außerdem ist in einem tatsächlichen System aufgrund der Oberflächenstreuung und der Korngrenzeneffekte in dem dünnen Goldfilm die Dämpfungskonstante des dünnen Goldfilms wahrscheinlich höher als die des massiven Goldes. Um den Einfluss der Dämpfungskonstante des dünnen Goldfilms zu berücksichtigen, zeigt Abb. 4b, dass die berechneten Absorptionsspektren der Dämpfungskonstanten des Goldfilms drei- und fünfmal höher sind als die des Volumengolds. Offensichtlich werden Absorptionspeaks mit unterschiedlichen Amplituden und FWHM beobachtet. Die Ergebnisse zeigen, dass der erhöhte Materialverlust von Metall ungünstig ist, um die Absorptionseigenschaften des vorgeschlagenen Schmalbandabsorbers weiter zu verbessern, die mit der früheren Forschung übereinstimmen [17].

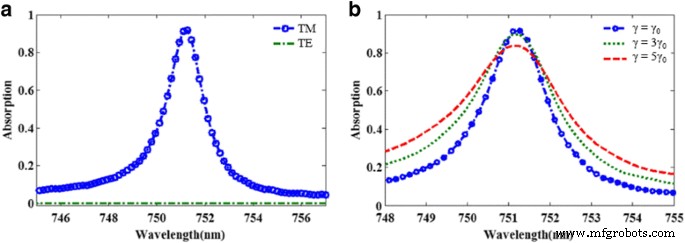
a Die Absorptionsspektren der vorgeschlagenen Struktur unter TE- und TM-Polarisationskonfigurationen. b Berechnete Absorptionsspektren in Abhängigkeit von der Dämpfungskonstante des Goldfilms

Es ist allgemein bekannt, dass die Eigenschaften des Metamaterial-Absorbers stark von der geometrischen Form und den strukturellen Abmessungen der Struktur beeinflusst werden. Zunächst untersuchen wir den Einfluss des dreieckigen Gold-Nanobands auf das Reflexionsspektrum der entworfenen Struktur. Das dreieckige Gold-Nanoband der Struktur wird entfernt oder in ein quadratisches bzw. halbelliptisches Gold-Nanoband umgewandelt, wie in Abb. 5c–e gezeigt, wobei die anderen Parameter in der Simulation unverändert bleiben. Die Reflexionsspektren dieser drei Strukturen werden analysiert und mit denen der Originalstruktur verglichen, wie in Abb. 5f–h jeweils gezeigt. Es ist leicht zu erkennen, dass die ursprüngliche Struktur eine schmalere FWHM und einen geringeren Reflexionsabfall erreichen kann als drei andere Strukturen. Um diese Ergebnisse besser zu verstehen, wird, wie in Abb. 5i–l gezeigt, die Magnetfeldverteilung (H) am Resonanzpeak dieser vier Strukturen jeweils aufgetragen und die Farbe zeigt die Intensität des Magnetfelds. Die magnetische Feldstärke der ursprünglichen Struktur ist offensichtlich stärker als die der drei anderen Strukturen. Dies bedeutet, dass LSPR in der ursprünglichen Struktur effizienter angeregt werden kann, was zu einem schmaleren FWHM und einem geringeren Reflexionsabfall führt.

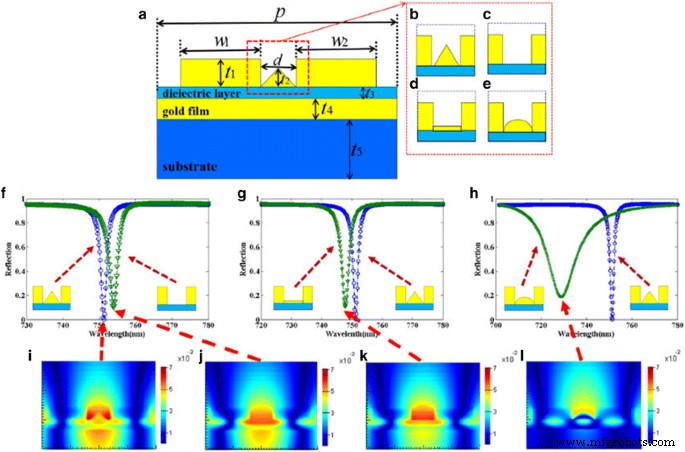
a–e Schema des vorgeschlagenen Metamaterials mit unterschiedlichen Nanostrukturen einer Elementarzelle. f–h Reflexionsspektren der verschiedenen Strukturen. ich–l Verteilungen des Magnetfeldes H am Resonanzpeak der entsprechenden Strukturen

Aus Abb. 5 ist die optische Leistung der ursprünglichen Struktur bei Verwendung von dreieckigen Nanobändern der der anderen Strukturen überlegen. Um einen weiteren Einblick in die Einflüsse der dreieckigen Nanobänder auf die optische Leistung zu erhalten, geben wir eine detaillierte Berechnung und Analyse für die in Abb. 6a gezeigte modifizierte Struktur, die ein trapezförmiges Nanoband mit dem gleichen Winkel θ<. enthält /i> zum dreieckigen Nanoband in Originalstruktur. Zunächst untersuchen wir, wie in Abb. 6b, c gezeigt, die optische Leistung der modifizierten Struktur in Abhängigkeit von verschiedenen Höhen h des trapezförmigen Nanobandes, wenn die Winkel θ bleiben unverändert. Wenn die Höhe h mehr als 10 nm beträgt, wird die optische Leistung der Struktur offensichtlich fast unverändert gehalten, was zeigt, dass die optische Leistung der Struktur bei der Herstellung robust ist. Da die Höhe h unter 5 nm liegt, nimmt der Reflexionsabfall zu, was damit erklärt werden kann, dass die Höhe h zu klein ist, was die effektive Fläche der Anregung von LSPR verringern würde. Wie in Abb. 6d, e gezeigt, untersuchen wir auch die optische Leistung der modifizierten Struktur in Abhängigkeit von verschiedenen Winkeln θ wenn die Höhe h auf 15 nm eingestellt ist. Es ist leicht zu beobachten, dass sich die optische Leistung der modifizierten Struktur mit dem großen Winkelbereich von 35° bis 68° wenig ändert. Allerdings nimmt der Reflexionsabfall offensichtlich unter dem Winkel θ . zu kleiner als 30°, woraus zu verstehen ist, dass der zu kleine Winkel θ kann die Anregungseffizienz von LSPR verringern. Somit wird durch die detaillierte Analyse der Einflüsse der verschiedenen Winkelparameter zwischen dem trapezförmigen Nanoband und den quadratischen Nanobändern auf die optische Leistung die perfekte Absorptionsleistung der ursprünglichen Struktur der Anregung von LSPR an der Ecke zwischen dem dreieckigen Nanoband zugeschrieben und die quadratischen Nanobänder, die gut mit den Ergebnissen des in Abb. 5i gezeigten Magnetfelds übereinstimmen. Gleichzeitig kann die Struktur gute optische Leistungen in einem großen Höhenbereich halten h und Winkel θ , was eine große Lockerung der Herstellungsrobustheit suggeriert und die Nanostruktur aus experimenteller Sicht realistischer macht. Unter Berücksichtigung der Herstellungsprozesse der eigentlichen Nanostruktur zeigt Abb. 6f schließlich die Geometrie der Struktur mit der Rauhigkeit der Gold/Dielektrikum-Oberfläche und der Passivierungsbehandlung für alle spitzen Winkel. Der Vergleich der optischen Leistung zwischen der modifizierten Struktur und der ursprünglichen Struktur wird berechnet und in Fig. 6g dargestellt. Offensichtlich ist der Einfluss der Fertigungstoleranz auf die Leistung der Nanostruktur sehr gering, was die robuste optische Leistung bei der Fertigung zeigt.

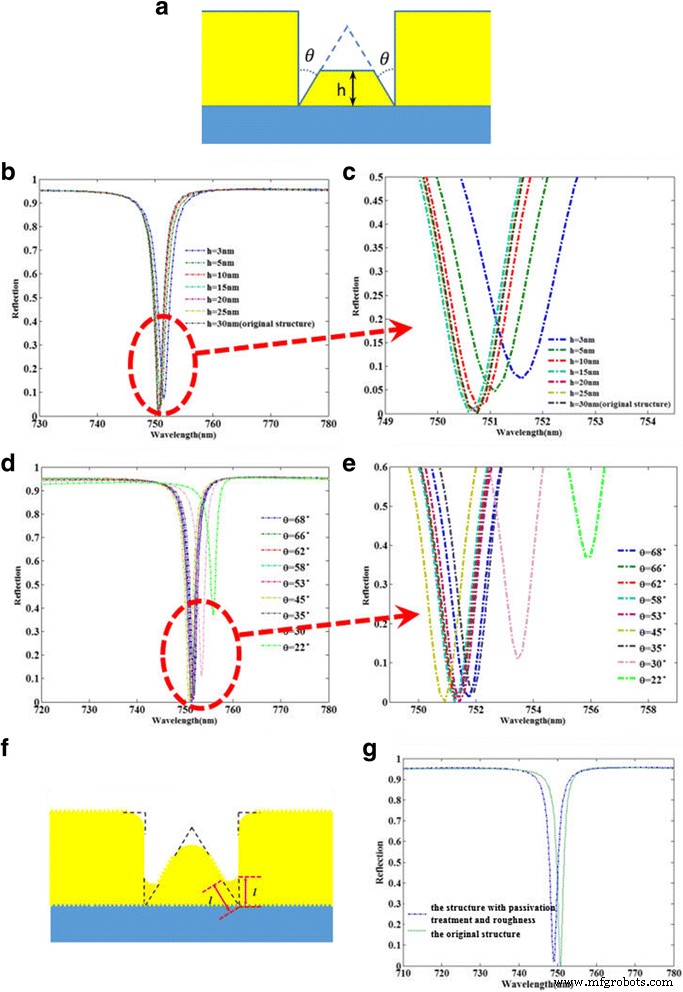
a Die modifizierte Struktur enthält ein trapezförmiges Nanoband mit dem gleichen Winkel θ zum dreieckigen Nanoband. b , c Vergleich der Reflexionsspektren zwischen den Nanostrukturen mit unterschiedlichen Höhen h , wenn die θ unverändert halten. d , e Vergleich der Reflexionsspektren zwischen den Nanostrukturen mit unterschiedlichen Winkeln θ , wenn die Höhe h = 15 nm. f Die modifizierte Struktur mit der Rauhigkeit der Gold/Dielektrikum-Oberfläche und der Passivierungsbehandlung für alle scharfen Winkel. g Vergleich der Reflexionsspektren zwischen der modifizierten Struktur und der ursprünglichen Struktur, wenn die l ist auf 3 nm festgelegt

Dann untersuchen wir auch die Auswirkungen der Strukturdimension und der Materialparameter mithilfe der FDTD-Methode auf das Reflexionsvermögen von Dip, FWHM und Resonanzwellenlänge der entworfenen Struktur. Mehrere Parameter werden untersucht, darunter Brechungsindex des Dielektrikums, Gold-Nanobandbreite w , die Goldnanobandbreite d , und die Dicke des Gold-Nanobands t ₁ . Abbildung 7 zeigt die Wirkung des Brechungsindex der dielektrischen Schicht auf das Reflexionsspektrum der Metamaterialstruktur. Wie in Abb. 7a gezeigt, verschiebt sich die Resonanzwellenlänge offensichtlich mit zunehmendem n . rot _Dielektrikum , was mit der Vorhersage des LC-Schaltungsmodells übereinstimmt. Wie in Abb. 5b gezeigt, wird der Reflexionsabfall zuerst verringert und dann erhöht, wenn n _Dielektrikum wird erhöht, während FWHM schmaler wird. Der FWHM- und Reflexionsgradabfall des Reflexionsspektrums hängt stark von der Kopplungsstärke zwischen den Nanobändern und dem Goldfilm ab, was zu unterschiedlichen optischen Leistungen mit verschiedenen dielektrischen Materialien des dielektrischen Abstandshalters zwischen den Nanobändern und dem Goldfilm führt. Der Reflektivitätsabfall ist der minimale Wert, wenn der Brechungsindex der dielektrischen Schicht ungefähr 1,3 beträgt. Gleichzeitig beträgt die FWHM etwa 1,85 nm, was viel schmaler ist als die des veröffentlichten Schmalbandabsorbers im sichtbaren Bereich [24, 28, 34, 39].

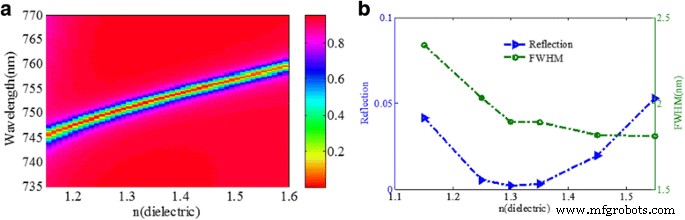
a Reflexionsspektren als Funktion des Brechungsindex der dielektrischen Schicht. b Reflektivität des Resonanzeinbruchs und FWHM als Funktion des Brechungsindex der dielektrischen Schicht

Abbildung 8 zeigt den Einfluss der Goldnanobandbreite w über das Reflexionsspektrum der Metamaterialstruktur. Wie in Abb. 8a gezeigt, wenn die Goldnanobandbreite w von 140 auf 177 nm ändert, verschiebt sich die Resonanzwellenlänge blau, was gut mit den Ergebnissen des äquivalenten LC-Schaltungsmodells übereinstimmt. Abbildung 8b zeigt, dass die FWHM schmaler wird und der Reflexionsabfall mit der Zunahme von w . zunimmt . Die Zunahme des Reflexionsabfalls kann sich aus der Zunahme der effektiven Metallfläche zum Reflektieren des einfallenden Lichts mit zunehmendem w . ergeben . Die Mindestwerte des Reflexionsabfalls und des FWHM können nicht gleichzeitig erhalten werden. In unserem Design ändern sich jedoch sowohl die Werte des Reflexionsabfalls als auch der FWHM geringfügig in einem weiten Bereich von w (140~162 nm), was für praktische Anwendungen günstig ist.

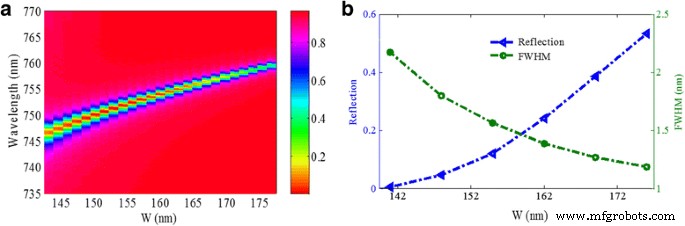
a Reflexionsspektren als Funktion der Gold-Nanobänder-Breite w . b Reflektivitätsabfall und FWHM als Funktionen der Gold-Nanobänder-Breite w

Darüber hinaus kann, wie in Abb. 9a gezeigt, der Reflektivitätsabfall einen niedrigeren Wert aufrechterhalten, wenn die Goldnanobandbreite d zwischen 55 und 75 nm liegt, während er deutlich ansteigt, wenn d 76 nm überschreitet, was erklärt werden kann, dass ein zu großer Abstand zwischen den beiden Nanobändern die Anregungseffizienz für LSPR verringern kann, wodurch die Absorptionseffizienz des einfallenden Lichts verringert wird. Der FWHM wird mit zunehmendem d . schmaler , und die optimale Größe von d liegt bei etwa 75 nm. Aus Abb. 9b kann der Reflektivitätsabfall einen niedrigeren Wert beibehalten, wenn die Gold-Nanobanddicke t ₁ ändert sich von 35 auf 50 nm, während die FWHM schmaler wird. Wenn jedoch t ₁ von 50 auf 60 nm erhöht, nimmt der Reflexionsabfall offensichtlich zu. Wir können das Ergebnis so verstehen, dass das Nanoband zu dick ist, das die Reflexion des einfallenden Lichts erhöhen würde. Abbildung 9c zeigt, dass der minimale Wert des Resonanzeinbruchs erreicht wird, wenn die dreieckige Goldhöhe t ₂ liegt bei etwa 30 nm. In dieser Struktur lag der Reflexionsabfall unter 0,025, wenn die dreieckige Goldhöhe im Bereich von 15 bis 40 nm liegt, was aufgrund der hervorragenden Robustheitsleistung für die Entwicklung einer Metamaterialstruktur von Vorteil ist.

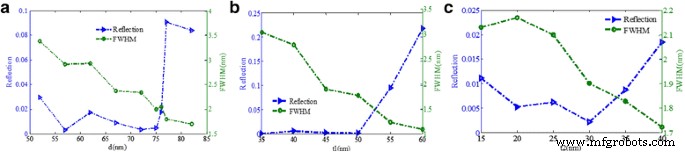
a Reflexionsabfall und FWHM als Funktionen der dreieckigen Gold-Nanobandbreite d . b Reflexionsabfall und FWHM als Funktion der Dicke der Gold-Nanobänder t ₁ . c Reflektivität des Resonanzeinbruchs und FWHM als Funktion der dreieckigen Goldhöhe t ₂

Es ist allgemein bekannt, dass die Resonanzwellenlänge der Metamaterialstruktur stark vom Brechungsindex des Umgebungsmediums abhängt, was in Sensoranwendungen weit verbreitet ist. Abbildung 10a zeigt, dass sich die Resonanzwellenlänge offensichtlich rot verschiebt, wenn der Brechungsindex der Umgebung zunimmt, was mit der Vorhersage des LC-Modells übereinstimmt, und der Reflexionsabfall gleichzeitig einen extrem niedrigen Wert halten kann. Wenn der RI von 1,07 auf 1,12 ansteigt, verschiebt sich die Resonanzwellenlänge von 733,828 auf 755.097 nm. Die berechnete Wellenlängenempfindlichkeit (S ) beträgt ungefähr 425 nm/RIU und die FWHM kann bis zu 1,82 nm betragen. Somit kann das FOM 233,5 erreichen. Soweit uns bekannt ist, ist der FOM viel höher als der des zuvor veröffentlichten plasmonischen Brechungsindexsensors im sichtbaren Bereich [24, 28, 34, 39]. Der vorgeschlagene plasmonische Brechungsindexsensor zeigt eine gute Linearität, wie in Abb. 10b gezeigt.

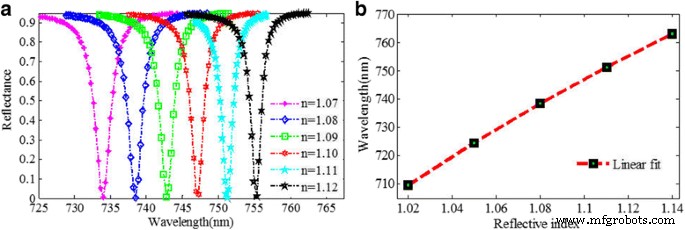
a Reflexionsspektren des plasmonischen Brechungsindexsensors mit verschiedenen Brechungsindizes der Umgebung. b Resonanzwellenlängenverschiebung gegenüber dem umgebenden Brechungsindex

In praktischen Anwendungen ist es normalerweise erforderlich, die relative Intensitätsänderung bei einer festen Wellenlänge mit den verschiedenen Brechungsindizes des umgebenden Mediums zu erfassen, und die entsprechende Gütezahl ist definiert als FOM* = max |(dI /dn )/Ich | [17]. Wie in Abb. 11a gezeigt, ändert sich der FOM* offensichtlich mit abnehmendem w , und das Maximum von FOM* kann 1,4 × 10 ⁵ . erreichen im w von etwa 358 nm. Abbildung 11b zeigt, dass der FOM mit abnehmendem d . zunimmt und ein Maximum von FOM* wird bei d . erreicht = 75 nm. Wie in Abb. 11c gezeigt, wenn die Goldnanobanddicke t ₁ 35 nm beträgt, ist die FOM* maximal. Darüber hinaus zeigt Abb. 11d auch, dass das Maximum von FOM* erreicht wird, wenn die dreieckige Goldhöhe t ₂ beträgt etwa 30 nm. Die Eigenschaften von FOM und FOM* mit den Änderungen der Strukturdimensionen werden numerisch untersucht, was eine gewisse Orientierung beim Design eines Hochleistungs-Plasmonensensors bieten kann.

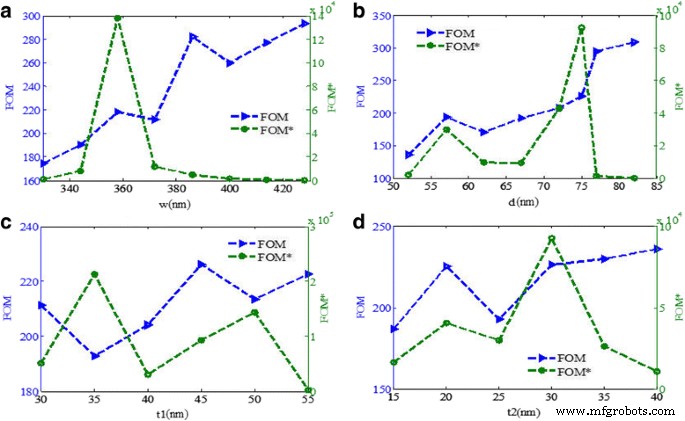
a–d FOM und FOM* als Funktionen der Gold-Nanobandbreite w , die dreieckige Gold-Nanobandbreite d , die Dicke der Gold-Nanobänder t ₁ , und die dreieckige Goldhöhe t ₂ , bzw.