Lichtleitfähigkeit, pH-Empfindlichkeit, Rauschen und Kanallängeneffekte bei Si-Nanodraht-FET-Sensoren

Hintergrund

In den letzten zehn Jahren wurden nanoskalige Siliziumstrukturen aufgrund ihrer vielversprechenden elektrischen, optischen, chemischen, thermischen und mechanischen Eigenschaften intensiv untersucht [1]. Im Vergleich zu größeren Strukturen ermöglichen nanoskalige Feldeffekttransistoren (FETs) die Messung elektrischer, optischer und anderer Arten von sehr kleinen Signalen aufgrund des erhöhten Oberfläche-zu-Volumen-Verhältnisses der Probe. Die kleinen Größen der Nanostrukturen machen sie ideal für die Erfassung kleiner Probenvolumina mit niedrigen Analytkonzentrationen. Die Merkmale und Eigenschaften von pH-Sensoren werden in [2–4] ausführlicher diskutiert. Es wird gezeigt, dass die pH-Empfindlichkeit von Siliziummassenmaterialien schlecht ist. Es wurden gute pH-Sensoreigenschaften von Si-Nanodrähten (NW) mit einer Empfindlichkeit von 58,3 mV/pH beobachtet. So können beispielsweise im Bereich der medizinischen Diagnostik nanoskalige Strukturen mit dem Ziel der Nutzung niederdimensionaler Nanostrukturen wie Carbon Nanotubes, metallische oder halbleitende NW oder atomgroße dünne Nanobänder (NR) für eine Vielzahl von Anwendungen realisiert werden [5] . Unter den genannten Strukturen eröffnen Silizium-NR- und NW-FET-Strukturen Perspektiven für den markierungsfreien, Echtzeit- und hochempfindlichen Nachweis von Biomolekülen unter Verwendung affinitätsbasierter Bindungsprinzipien [6]. Die Sensitivität verschiedener NR-Dimensionen wurde untersucht. Es konnte gezeigt werden, dass der neue Sensor mit integriertem Referenz-NR zur Echtzeit-Fehlerüberwachung bei der pH-Messung eingesetzt werden kann [6]. Die elektronischen Geräte werden ständig um neue Merkmale und Funktionen erweitert, wie zum Beispiel mobile Systeme zur Gesundheitsüberwachung und tragbare Geräte. Trotz des Erfolgs solcher persönlicher Gesundheitsüberwachungssysteme [7] wird erwartet, dass die nächste Generation tragbarer Geräte auch ein tragbares „Lab-on-a-Chip“ enthält – ein Satz medizinischer Biosensoren, die zur Erkennung und Diagnose verschiedener medizinische Substanzen [8, 9]. Um frühe Krankheitsstadien im Idealfall auf Einzelmolekülebene überwachen und erkennen zu können, muss die Größe des Sensorwandlers mit den zu testenden biologischen Markern vergleichbar sein. Daher müssen auf NWs und NRs basierende Biosensoren für die Überwachung biologischer Ereignisse entwickelt werden, die in sehr kleinen Dimensionen auftreten. Ein weiteres wichtiges Anwendungsgebiet ist die Optoelektronik, wo die Lichtwechselwirkung mit Nanostrukturen für zukünftige optische Geräteanwendungen genutzt werden kann. Subwellenlängen-Durchmesser und Proximity-Effekte können zu verbesserten optischen Eigenschaften führen, wie beispielsweise einem geringen Reflexionsvermögen und damit einer hohen Absorption. Untersuchungsergebnisse der optischen Si-NW-Absorption haben die starken größenabhängigen Effekte gezeigt [10–12]. Untersuchungen der optischen Breitbandabsorption zeigten erhöhte optische Gesamtabsorptionsspektren für Si-NW-Proben [13]. Si-NWs führen zu einer signifikanten Reduktion des Reflexionsvermögens im Vergleich zu den festen Siliziumschichten [13, 14]. Die optische Absorption nimmt zu, während die Wellenlänge abnimmt. Es sollte beachtet werden, dass nanoskalige Si-Strukturen im Gegensatz zum Volumenmaterial Halbleiter mit direkter Bandlücke sein können, was sie zu einer ausgezeichneten Wahl für optische Anwendungen macht [11, 13, 15–18]. Andererseits vergrößert die Größenskalierung die Bandlücke [15]. Dies kann zu einer erfolgreichen Verschiebung der Absorptionsspektren zu kurzen Wellenlängen führen [11, 18]. Bei Abnahme der Baugröße müssen auch die Beschränkungen bezüglich Strom und Spannung berücksichtigt werden. Bei Geräten, die mit schwachen Signalpegeln arbeiten, spielt das interne Rauschen eine entscheidende Rolle [4, 19, 20, 21]. Es bestimmt einen der wichtigsten Parameter von Sensoren – das Signal-Rausch-Verhältnis (SNR). Wie für SiNW-Sensoren mit doppeltem Gate gezeigt, steigt die pH-Empfindlichkeit mit der Liquid Gate-Spannung und das SNR hat einen höheren Wert (~ 10 ⁵ ) [11, 18]. Der Nanoband-Ansatz eröffnet die Möglichkeit zur großtechnischen CMOS-Fertigung hochempfindlicher Biomolekül-Chips für den potenziellen Einsatz in Medizin und Biotechnologie [22].

Neueste Forschungen zu nanoskaligen Materialien haben gezeigt, dass sich elektronische, magnetische, thermische und optische Eigenschaften dramatisch unterscheiden können, wenn ihre eindimensionalen Formen synthetisiert werden. Nanodrähte, die aus ein- oder wenigen Atomen dicken lamellaren Kristallen gewonnen werden, sind neuartige Formen eindimensionaler nanoskaliger Materialien und ideale Systeme zur Untersuchung der Größenabhängigkeit der fundamentalen Eigenschaften.

Eine detaillierte Analyse der neuesten Errungenschaften zu Synthesemethoden und theoretischen Studien der NR wird in [23] präsentiert. In der Literatur wurden die Effekte der Photoleitfähigkeit, der pH-Empfindlichkeit, des Rauschens und der Kanallänge im gleichen Satz von NW-FET-Arrays nicht im Detail untersucht. Die Oberflächenrauhigkeit und der Beitrag der dielektrischen Schichten können jedoch die Struktureigenschaften in Abhängigkeit von der Herstellungstechnologie, die für verschiedene Gerätesätze angewendet wird, erheblich verändern. In dieser Hinsicht ist das Verständnis der Kanallängeneffekte in demselben Satz von NW-FETs wichtig für die Entwicklung von Geräten mit erweiterter Funktionalität.

Die vorliegende Arbeit widmet sich der Untersuchung von Silizium-Nanodraht-basierten FETs, einschließlich der Probenherstellungstechnologie, und der Chip-Charakterisierung, ihrer dunklen und hellen Strom-Spannungs-Eigenschaften (I-V) und der pH-Empfindlichkeit. Die Auswirkungen des Kanallängeneinflusses auf die Source-Drain-Ströme, die pH-Empfindlichkeit und das niederfrequente Rauschen werden beschrieben. Wir zeigen, dass Silizium-Nanodrähte, die auf der Basis einer dünnen Siliziumschicht auf einem oxidierten Siliziumsubstrat hergestellt werden, eine hohe pH-Empfindlichkeit ziemlich nahe der Nernst-Grenze aufweisen können.

Methoden/experimentell

Silizium-NW-Strukturen wurden auf der Basis von Silizium-auf-Isolator(SOI)-Wafern hergestellt, die von SOITEC bezogen wurden. Der Prozess beginnt mit der thermischen Oxidation zu 20 nm dicken Siliziumoxid-Hartmasken. Die Dicke der aktiven Siliziumschicht beträgt 50 nm. NWs verschiedener Geometrien werden dann mittels optischer Lithographie in einer Hartmaske strukturiert und in SiO₂ . übertragen Schicht unter Verwendung eines reaktiven Ionenätzverfahrensschrittes. Das Muster wird verwendet, um Silizium-Nanobänder und -Nanodrähte durch nasschemisches Ätzen in der Tetramethylammoniumhydroxid (TMAH)-Lösung zu erhalten. Die Gatedielektrikumsschicht, die auch als Kanalschutz vor einer flüssigen Umgebung dient, besteht aus thermisch gewachsenem 8 nm dickem Siliziumoxid. Der NW-Kanal bestand aus fast undotiertem Silizium mit einer Lochkonzentration von etwa 10 ¹⁵ cm ⁻³ . Source- und Drain-Kontakte wurden hochdotiert, um gute ohmsche Kontakte zu bilden. Für die Anbindung an die Elektronik wurden Aluminiumkontakte im Lift-Off-Verfahren strukturiert. Schließlich wurden die Chips mit einer Polyimidschicht (PI) passiviert, um Metallzuleitungen vor einer flüssigen Umgebung zu schützen. Abbildung 1 zeigt schematische Bilder der untersuchten Proben im pH-Sensor-Betriebsmodus (a) und Fotoempfänger-Betriebsmodus (b), und ein REM-Bild der untersuchten NW ist in Abbildung 2 dargestellt.

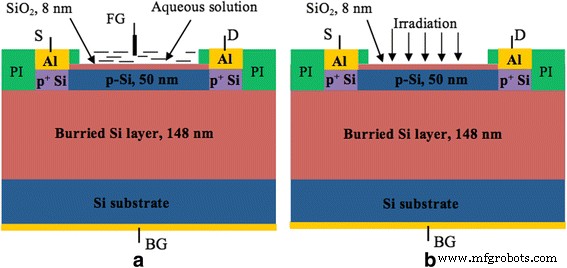
Untersuchung von Si-Nanodraht-Feldeffekttransistorstrukturen. Schematische Darstellung der untersuchten Proben:pH-Sensor-Betriebsmodus (a ) und Fotoempfänger-Betriebsmodus (b ). PI Polyimidschicht, S Source, D Drain, FG Front Gate (Referenzelektrode, RE), BG Back Gate

SEM-Bild einer Si-NW-FET-Struktur. Typische rasterelektronenmikroskopische (REM) Aufnahme einer hergestellten Si-Nanoband-Feldeffekttransistorstruktur

Ergebnisse und Diskussion

Strom-Spannungs-Eigenschaften und pH-Empfindlichkeit

Die Abbildungen 3 und 4 zeigen die Source-Drain-Strom-Spannung (I-V)-Kennlinien der untersuchten Proben, die bei Back-Gate-Spannungen von − 1 bzw. − 5 V gemessen wurden. Die Eigenschaften wurden unter dunklen Bedingungen sowie unter spezifischen Beleuchtungsstärken von 0,85 und 1,6 W/cm ² . gemessen bei Raumtemperatur. Die Lichtanregung erfolgt mit Glühlampen, die sich im Abstand von 15 cm vom Sensor befinden. Die I-V-Abhängigkeiten zeigen ein typisches Verhalten, das den Metall-Oxid-Halbleiter-FETs (MOSFETs) [24] ähnelt, da die untersuchten Proben relativ große Abmessungen von l . haben × w × t = (2 ÷ 10) × 10 × 0.05 μm (l , w , und t sind die Kanallänge, -breite und -dicke entsprechend). I-V-Kurven in den Fign. 3 und 4 können wie folgt beschrieben werden:

wo ich _{ds, d} und ich _{ds, ph} sind die Dunkel- und Photo-Source-Drain-Stromkomponenten. Dunkelstrom kann durch den bekannten Ausdruck für MOSFETs für V . beschrieben werden _ds V _gs − V _te [24]:

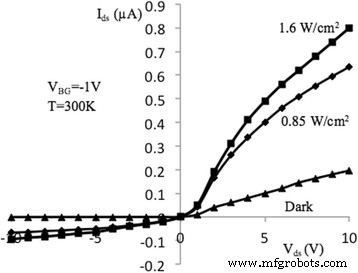
I–V-Charakteristik von NW FET, gemessen bei optischer Anregung (V _BG = − 1 V). Ausgangsstrom-Spannungs-Kennlinie der NW-FET-Probe mit der Länge l = 10 μm, gemessen im Dunkeln und bei Anregung durch das Licht spezifische Leistung 0,85 und 1,6 W/cm ² , um T = 300 K und V _BG = − 1 V

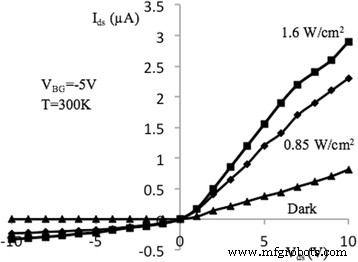
I–V-Charakteristik von NW FET, gemessen bei optischer Anregung (V _BG = − 5 V). Ausgangsstrom-Spannungs-Kennlinie der NW-FET-Probe mit der Länge l = 10 μm, gemessen im Dunkeln und bei Anregung durch das Licht spezifische Leistung 0,85 und 1,6 W/cm ² um T = 300 K und V _BG = − 5 V

Hier, C _Ochse = ε _Ochse /t _Ochse ist die Kapazität der Oxidschicht pro Flächeneinheit, ε _Ochse und t _Ochse sind die Permittivität und Dicke der Gateoxidschicht, μ _n die Elektronenmobilität ist und V _ds , V _gs , und V _te sind entsprechend Source-Drain-, Gate-Source- und Schwellenspannungen. Die Erzeugungsrate von Fototrägern ist gleich ηαN _ph , wobei N _ph = W /hν ist die Strahlungsintensität. Bei niedrigen Injektionsniveaus und konstanter Lebensdauer der Löcher beträgt die Konzentration der Phototräger \(\Updelta p=\eta\alpha{\tau}_p\frac{W}{h\nu}\) [25]. Die Ladungsträger driften bei angelegter Spannung V _ds . In diesem Fall kann der Photostrom dargestellt werden als:

Hier, A _ch = wt ist die aktuelle Kanalquerschnittsfläche, e ist die Elektronenladung, ∆p und μ _p sind die Konzentration und Beweglichkeit überschüssiger Phototräger (Löcher), α der Beleuchtungsabsorptionskoeffizient, η die Quantenausbeute, τ _p die Lebensdauer des Lochs, hν die Photonenenergie und W die spezifische Beleuchtungsleistung in [W/cm ² ].

In Gl. (3) angenommen, dass die elektrische Feldstärke gleichmäßig über die Kanallänge verteilt ist und der Wert von A _ch aufgrund der hohen Kanalleitfähigkeit leicht über die Länge des Kanals variiert. Es sollte beachtet werden, dass diese Annahme im Hauptteil des Kanals gilt, der weit von Source- und Drain-Kontakten entfernt ist.

Bei niedrigen Spannungen V _ds , der Source-Drain-Strom I _ds wächst ungefähr linear mit der Spannung. Mit zunehmender spezifischer Lichtleistung wird die Größe des I _ds steigt. Die Abbildungen 5 und 6 zeigen I-V-Kurven des untersuchten Bauelements bei den verschiedenen Front-Gate-Spannungen (V _FG =  − 1 V, − 5 V) gemessen in wässriger Lösung mit pH = 6.2, 7 und 8.3. Wir können sehen, dass eine Erhöhung des pH-Werts zu einer Erhöhung des Kanalstroms führt,I _ds . Dies stimmt gut mit dem Modell des Lösungskontakts mit der Oxidschichtoberfläche überein, dann an der Oxid/Lösungs-Grenzfläche verursachte Hydroxylgruppen SiOH. Konzentration und Verhalten dieser Hydroxylgruppen hängen vom pH-Wert ab. Der Fall, in dem die Oberfläche nicht geladen ist, wird als Nullladungspunkt bezeichnet. Für das SiO₂ dielektrischer Schicht wird der Punkt bei pH = 2,2 erreicht. Bei pH-Werten kleiner 2,2 wird die Oxidoberfläche positiv geladen; bei höheren pH-Werten wird die Oxidoberfläche negativ geladen. Bei Pufferlösung mit pH = 7 wird die Oberflächenladung des Siliziumoxids negativ geladen. Daher steigt bei angelegtem negativem Gate-Potential der Absolutwert der negativen Ladung auf dem Oberflächenoxid. Als Ergebnis steigt die Majoritätsträgerkonzentration im Stromkanal (Löcher in p-Si) und somit steigt der Kanalstrom.

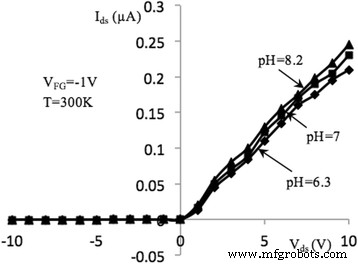
I–V-Eigenschaften von NW FET, gemessen in verschiedenen pH-Lösungen (V _FG = − 1 V). Ausgangsstrom-Spannungs-Kennlinie des NW-FET mit Länge, l = 10 μm, gemessen im Dunkeln und pH-Konzentrationen:6,3, 7, 8,2 bei T = 300 K, V_BG = − 5 V und V _FG = − 1 V

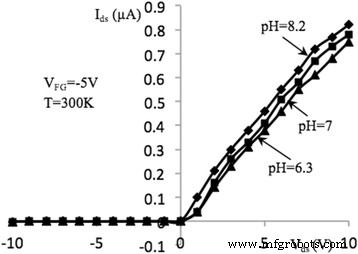
I–V-Eigenschaften von NW FET, gemessen in pH-Lösungen (V _FG = − 5 V). Ausgangsstrom-Spannungs-Kennlinie des NW-FET mit Länge, l = 10 μm, gemessen im Dunkeln und pH-Konzentrationen 6,3, 7, 8,2 bei T = 300 K, V _BG = − 5 V und V _FG = − 5 V

Die Abbildungen 5 und 6 zeigen die I-V-Eigenschaften der Si-NW-Strukturen, die im biochemischen Sensormodus arbeiten. Für jeden pH-Wert wurden viermal Messungen durchgeführt. Die Wiederholbarkeit lag innerhalb von 7%. In [26] wurde die pH-Empfindlichkeit der biochemischen Sensoren eingeführt als

Hier, ∆ich _ds und ∆pH sind die elementaren Änderungen in I _ds und pH-Wert. Beachten Sie, dass die pH-Empfindlichkeit der messbare Wert ist. Im Lösungsmedium mit erhöhtem pH-Wert erhöht sich der Source-Drain-Strom. Dies ermöglicht die Registrierung der pH-Variation in beliebigen Bioflüssigkeiten (innerhalb des für physiologische Lösungen relevanten Lösungsbereichs) mit hoher Genauigkeit. Zum Beispiel für V _BG =  − 5 V bei V _ds = 5 V, die Empfindlichkeit ist gleich R _pH ≈ 56,4 mV/pH. Am V _BG =  − 5 V steigt die pH-Empfindlichkeit auf 59,3 mV/pH an und nähert sich der Nernst-Grenze von 59,5 mV/pH [24]. Die pH-Empfindlichkeit wächst mit steigender Back-Gate-Spannung. Zum Beispiel aus den Abb. 5 und 6 bei V _ds = 8 V erhalten wir das Verhältnis \( {\left({R}_{\mathrm{pH}}\right)}_{V_{\mathrm{BG}}=-5\ \mathrm{V}}/ {(R)}_{V_{BG}=-1\ \mathrm{V}}\approx 5,17 \), dh ungefähr fünfmal verbesserte Empfindlichkeit.

Niederfrequente Rauschspektren und -merkmale durch Bestrahlung und pH-Änderungen

Die Rauschspektren von Si-NW-Strukturen wurden bei konstantem Strom im ohmschen Modus gemessen. Abbildung 7 zeigt die spektrale Dichte der Drainstrom-Rauschleistung, gemessen unter dunklen Bedingungen sowie unter Bestrahlung mit einer angelegten Back-Gate-Spannung von V _BG =  − 1 V bei I _ds = 0,1 μA. Geräuschspektren, gemessen im Dunkeln, zeigen 1/f ^γ Rauschverhalten mit Rauschparameter gleich γ =1. Der Niederfrequenz-(LF)-Rauschpegel steigt mit der Zunahme der Lichteinstrahlungsintensität. Die Erhöhung der Beleuchtungsintensität führt zu einer Zunahme der Konzentration des Hauptträgers. Dies wiederum verursacht das Anwachsen von Mobilitätsfluktuationen im Kanal aufgrund erhöhter Wechselwirkungs- und Streuraten als Ergebnis der Streuung erstens zwischen Trägern und zweitens zwischen Trägern und akustischen Phononen sowie an verschiedenen Störstellenfallen [27].

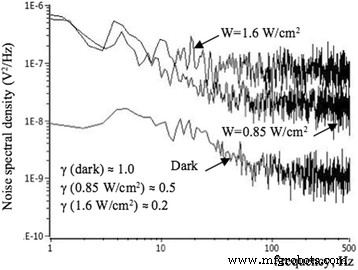
Rauschspektren von NW FET, gemessen bei optischer Anregung. Spektrale Abhängigkeit des NF-Rauschens, gemessen für eine NW-FET-Probe mit l = 10 μm unter Beleuchtung:0,85 W/cm ² , 1,6 W/cm ² , und im Dunkeln; V _BG = − 1 V, T = 300 K

Da die Rauschmessungen bei konstantem Strom im ohmschen Modus durchgeführt wurden, ändert sich der Kanalwiderstand linear mit der angelegten Spannung V _ds . Bekanntlich ist die spektrale Dichte des 1/f-Rauschens S _V ist proportional zur Spannung in Leistung 2:

Hier, α _H ist der Hooge-Parameter, R _ch ist der aktuelle Kanalwiderstand; Ω = A _ch l ist die Lautstärke des aktuellen Kanals; ρ ist der kanalspezifische Widerstand. Die Verringerung des Kanalwiderstands führt zu einer Zunahme der spektralen Rauschdichte. Bei der Lichtanregung einer Nanodraht-FET-Probe mit Leistung W , wir haben:

Hier, p _d ist die Konzentration von Löchern im Dunkeln und σ ist die spezifische Leitfähigkeit. Der Geräuschpegel steigt proportional zur Intensität der Beleuchtung.

Wir berechnen Werte des Rauschparameters γ , unter Verwendung der in Abb. 7 dargestellten Kurven. Die folgenden Parameter werden für Proben erhalten, die im Dunkeln und bei Lichtanregung unterschiedlicher Leistung gemessen wurden:

γ (dunkel) ≈ 1.0, γ (0,85 W/cm ² ) ≈ 0.5 und γ (1,6 W/cm ² ) ≈ 0.2.

Bei Bestrahlung ist der Wert des Rauschparameters γ sinkt. Dies lässt sich wie folgt erklären. Mit steigender Lichtleistung steigt die Leitfähigkeit des Stromkanals. Als Ergebnis ist die effektive Lebensdauer von Minoritätsladungsträgern τ _ef steigt und erreicht Werte τ _ef ≥ (10 ⁻³ ÷ 10 ⁻² ) S. Sobald die Elektron-Loch-Paare durch Absorption in Silizium erzeugt wurden, müssen mehrere Rekombinationsmechanismen berücksichtigt werden. Diese Prozesse laufen parallel ab, und die Rekombinationsrate ist die Summe der Raten, die dem einzelnen Prozess entsprechen. Verschiedene Lebensdauern sind mit unterschiedlichen Rekombinationsmechanismen verbunden. Die effektive Lebensdauer des Ladungsträgers muss durch die Oberfläche des Ladungsträgers, die Strahlung, das Volumen (Masse) und die Lebensdauer der Auger-Rekombination bestimmt werden. Es ist bekannt, dass die Strahlungslebensdauer umgekehrt proportional zur Ladungsträgerdichte ist und die Auger-Lebensdauer umgekehrt proportional zum Quadrat der Ladungsträgerdichte [28]. Die Rekombinationslebensdauer wird durch den Shockley-Read-Hall-Rekombinationsmechanismus bestimmt. Sie ist für niedrige Ladungsträgerdichten konstant und nimmt für hohe Injektionspegel zu [29,30,31]. Es ist bekannt, dass die Lebensdauer der Oberflächenrekombination proportional zur Geschwindigkeit der Oberflächenrekombination und umgekehrt proportional zur Dicke der Probe ist [29, 32, 33].

Das Verhalten der effektiven Lebensdauer ist komplex, abhängig von der Dichte des Nichtgleichgewichtsträgers und den Rekombinationsmechanismen. Wenn die Ladungsträgerdichte zunimmt, kann die effektive Lebensdauer entweder eine konstante oder eine abnehmende Funktion sein [29]. Bei Nanodrähten mit einem hohen Verhältnis von Oberfläche zu Volumen spielen die Oberflächengrenzflächenzustände eine wichtigere Rolle und ihr Beitrag dominiert. Darüber hinaus kann es andere Arten der Rekombination übertreffen. Andererseits kann die Rekombinationslebensdauer bei moderater Trägerdichte auch zunehmen. In unserem Fall von Silizium-NW-Trägern wird die effektive Lebensdauer im Wesentlichen durch die Oberflächen- und Volumenrekombination und die Zunahme mit dem Dichtewachstum des Trägers bestimmt.

Bekanntlich hat das Generations-Rekombinations-(g-r)-Rauschen die Lorentzsche Form [19, 34]:

Hier, f ist die Frequenz. Es ist klar, dass der Abschnitt des Plateaus von der Abhängigkeit S _{V , g − r} (f ) wird durch die Bedingung bestimmt

wo f _c ist die charakteristische Frequenz. Es ist zu beachten, dass mit zunehmender Elektronenlebensdauer der Wert der Grenzfrequenz f _c sinkt. Die charakteristische Frequenz des g-r-Rauschens verschiebt sich in den Niederfrequenzbereich. Da die Leitfähigkeit σ und Lebensdauer τ _n mit zunehmender Beleuchtungsleistung zunehmen, die f _c nimmt mit zunehmendem W . ab , entsprechend:

Die g-r-Prozesse führen zur Abschirmung des 1/f-Rauschanteils unter dem g-r-Rauschplateau. Die Tatsache erklärt die Abnahme des Wertes des Rauschparameters γ mit zunehmender Beleuchtungsleistung.

Abbildung 8 zeigt die spektrale Abhängigkeit des NF-Rauschleistungsspektrums einer Si-NW-FET-Probe, gemessen bei V _FG =  − 1 V, I _ds = 0,1 μA in Lösung bei den verschiedenen pH-Werten:6,3, 7,0 und 8,2. Der Geräuschparameter nimmt mit steigendem pH-Wert ab:γ (pH = 6,3) ≈ 1,0; γ (pH = 7,0) ≈ 0,5; γ (pH = 8,2) ≈ 0,4. Die Steigungen wurden im Bereich von 10 bis 500 Hz berechnet. Der NF-Geräuschpegel steigt und seine Steigung nimmt mit steigendem pH-Wert ab. Der Anstieg des pH-Wertes führt zu einer Abnahme des Kanalwiderstands, der durch die Ansammlung negativer Ladungen an der Halbleiter-Oxid-Grenzfläche verursacht wird. Abnahme der Steigung von S _V (f ) kann die Abhängigkeit mit steigendem pH unter Berücksichtigung des Effekts der Kanalleitfähigkeitserhöhung erklärt werden.

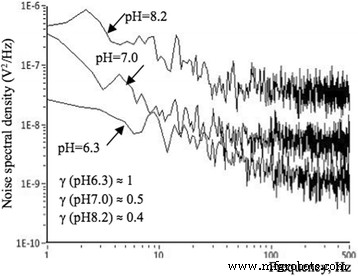
Rauschspektren von NW FET, gemessen in verschiedenen pH-Lösungen. Spektrale Abhängigkeit des NF-Rauschens für NW mit der Länge, l = 10 μm, gemessen bei T = 300 K und mehrere pH-Werte:6,3, 7,0 und 8,2 bei V _BG = − 5 V, V _FG = − 1 V

Auswirkungen der Kanallänge

In diesem Abschnitt präsentieren wir die Ergebnisse zum Einfluss der aktuellen Kanallänge auf die Transportmechanismen, die pH-Empfindlichkeit und auch auf das Verhalten des NF-Rauschens der Si-NW-basierten Sensoren. Die Stromstärke ist umgekehrt proportional zur Länge des Stromkanals, was die Anwendung der Drift-Approximation für den Transportmechanismus sowie die Annahme einer gleichmäßigen Verteilung der elektrischen Feldstärke über die Länge des Stromkanals rechtfertigt ( Abb. 9). Der Einfluss der Lichtanregung führt zu einer Erhöhung des Source-Drain-Stroms. Die pH-Empfindlichkeit steigt mit der aktuellen Kanallänge und tendiert zum Nernst-Limit von 59,5 mV/pH (Abb. 10), was gut mit Werten für Mikrosensoren übereinstimmt [27]. Unsere Ergebnisse unterstützen auch Beobachtungen des pH-Sensitivitätsverhaltens, die für NW-Proben mit unterschiedlichen Geometrien erhalten wurden [6]. Der in unserer Arbeit systematisch untersuchte Längeneffekt lässt sich wie folgt erklären. Da die Länge des Kanals l nimmt die Fläche der pH-sensitiven Oberfläche ab und folglich die Anzahl der messbaren H ⁺ Ionen in der wässrigen Lösung nimmt ab. Nach Gl. (2), das aktuelle Ich _ds steigt mit abnehmendem l , was zu einer Abnahme des Widerstands des Stromkanals bei konstanter Spannung V . führt _ds . Als Widerstand des Kanals R _ch nimmt ab, seine Modulation wird unter dem Einfluss des H ⁺ . behindert Ionen; daher nimmt die pH-Empfindlichkeit ab.

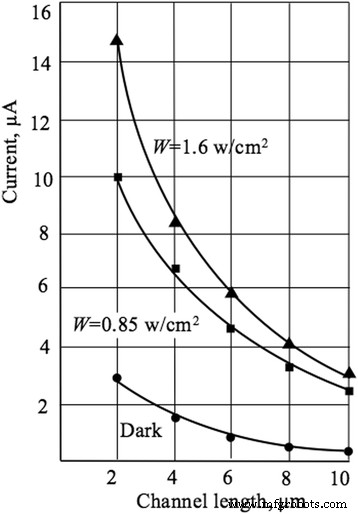
Kanalstrom von NW FET vs. Länge. Darstellung des Kanalstroms als Funktion der Kanallänge. V _BG = − 5 V, V _ds = − 5 V, R _ch = 1,26 MΩ

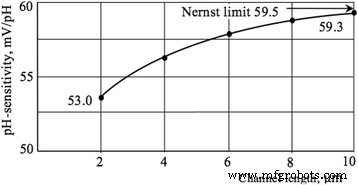
pH-Empfindlichkeit vs. Kanallänge. Auftragung der pH-Empfindlichkeit als Funktion der Kanallänge. V _FG = − 10 V, V _BG = − 5 V, V _ds = − 5 V, R _ch = 1,26 MΩ

Abbildung 11 zeigt die Abhängigkeit der spektralen Dichte des NF-Rauschens von der Länge des aktuellen Kanals.

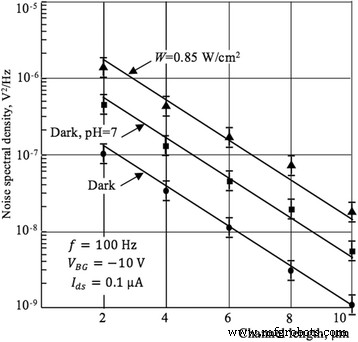
Spektraldichte Rauschen im Vergleich zur aktuellen Kanallänge. Plot der spektralen Rauschdichte als Funktion der aktuellen Kanallänge. Für pH-Messungen V _FG = − 10 V

Diese Kurven werden unter Verwendung der spektralen Abhängigkeiten des NF-Rauschens, gemessen für Si-NWs mit unterschiedlichen Längen im Dunkeln, unter Beleuchtung mit einer Intensität von 0,85 V/cm ² . aufgetragen , und in einer wässrigen Lösung mit einem pH = 7 Der berechnete Wert der Steigung der parallelen Kurven (Abb. 10) ist gleich log(500/10) ≈ 2.7. Dieser Wert liegt nahe dem Wert (gleich 3), der theoretisch unter Verwendung von Gl. (6) und (7), S _V l ⁻³ mit Fehler etwa 10 %. Die Ergebnisse zeigen, dass das theoretisch vorhergesagte S_V (l ) stimmen unter Berücksichtigung des relativ hohen thermischen Rauschens gut mit den gemessenen Eigenschaften überein. Nach Gl. (6), Skalierung der Kanallänge l nach unten führt zu einer Verringerung des Widerstands und einer Stromerhöhung, was einer Erhöhung der Ladungsträger im Kanal entspricht. This, in turn, results in increased interaction of charge carriers with traps on the interface between silicon and dielectric layer. Thus, the noise level increases, which is also confirmed by experimental dependences (see Fig. 11).

The non-Nernstian pH-response of SiO₂ -gated FET-based sensors has been a major topic since the introduction of the ion-sensitive FET (ISFET) concept. The sensitivity of the SiNR FET sensor to changes in pH can be quantified by measuring the shift of the threshold voltage of the device and is defined by the Nernst equation [35]:

\( \frac{\delta {\Psi}_0}{\delta \mathrm{pH}}=-2.3\frac{kT}{q}\alpha \le 59\ \frac{mV}{\mathrm{pH}} \),

wo δ Ψ₀ is the potential at the surface. The dimensionless parameter a which depends on the intrinsic buffer capacity of the oxide surface and the differential double-layer capacitance can be a value between 0 and 1.

Changes in the pH of the solution induce variations in the surface charge density and surface potential. It leads to a change in the NR channel conductance. In general, sensitivity is defined as the largest possible output response to a certain biological event. The pH sensitivity of BioFETs arises from the acid/base reactions at the oxide/electrolyte interface and the maximum pH response achievable by a conventional ISFET is the Nernst limit of 59 mV/pH. Over the years, there have been numerous reports [36,37,38,39,40,41,42,45] on devices with near Nernstian. The high sensitivity was achieved either by optimization of the intrinsic device transfer characteristics (such as lowering of the subthreshold swing or by tuning the gate potential) or by chemical surface modifications. Decreasing silicon thickness leads to higher surface charge sensitivity [45]. In [6], it is shown that at an optimum thickness of 30 nm the sensitivity reaches maximum value, and for a thicker device layer the pH response decreases and the largest response is obtained from the widest NR FET with the highest surface area. The most popular platform for chemical modification of SiO₂ surface is chemisorption of a few nanometer thick self-assembled monolayers [46], not only to enhance the pH sensitivity of Si/SiO₂ gated nanosensors [47], but also because biomolecules such as proteins [48] or DNA [49], which can be coupled to the other functional end of certain monolayers. Authors of Ref. [50] discussed the results concerning the functionalization and modification of SiNW FET sensors.

Schlussfolgerungen

Silicon nanowire FET biochemical sensors of various lengths were fabricated. The static dark and light-illuminated I–V curves as well as the behavior of these sensors in an aqueous solution with different values of pH are investigated. The static dark I–V dependencies demonstrate FET behavior. With increasing light intensity, the source-drain current grows because of the increase in the conduction of the current channel. The pH sensitivity increases with the increasing of the back-gate voltage and approaches to 59.5 mV/pH. The magnitude of the channel current is approximately inversely proportional to the length of the current channel and the pH sensitivity increases with increase of channel length approaching to the Nernst limit value, indicating that larger area devices are more suitable for the pH sensing.

The spectral density of the LF noise increases both under the action of the pH solution and the illumination, and in both cases, the frequency dependence of the noise is weakened and the value of the noise parameter γ decreases. With increasing of the pH value and illumination power, the 1/f-noise is screened by the g-r plateau. The characteristic frequency of the g-r noise component decreases with increasing illumination power. LF noise level increases and its slope decreases with increase of the pH value. It is shown that the measured value of the slope of noise spectral density dependence on the current channel length is 2.7 that is close to the theoretically predictable value 3 within 10% error.

Abkürzungen

FETs:

Field-effect transistors

LF:

Low-frequency

NWs:

Nanowires

TMAH:

Tetramethylammonium hydroxide