Spin- und Valley-abhängige elektronische Struktur in Silicen unter periodischen Potentialen

Hintergrund

Zweidimensionale (2D) Dirac-Materialien mit hexagonalen Gitterstrukturen werden seit der Entdeckung von Graphen intensiv erforscht, wie Silicen [1, 2], Übergangsmetalldichalkogenide [3, 4] und Phosphoren [5]. Obwohl Graphen viele besondere Eigenschaften hat, wird seine Anwendung durch die Nullbandlücke und die schwache Spin-Bahn-Wechselwirkung (SOI) eingeschränkt. Vor kurzem wurde ein Silizium-Analogon von Graphen, Silicen, durch epitaktisches Wachstum hergestellt [6–10], und seine Stabilität wurde durch theoretische Studien vorhergesagt [11, 12]. Graphen und Silicen haben ähnliche Bandstrukturen um K und K ^′ Täler, und die niederenergetischen Spektren von beiden werden durch die relativistische Dirac-Gleichung [13] beschrieben. Im Gegensatz zu Graphen hat Silicen eine starke intrinsische SOI und eine geknickte Struktur. Der starke SOI könnte an Dirac-Punkten eine Lücke öffnen [13, 14] und zu einer Kopplung zwischen den Spin- und Valley-Freiheitsgraden führen. Die geknickte Struktur ermöglicht es uns, die Bandlücke durch ein externes elektrisches Feld senkrecht zur Silicenschicht zu kontrollieren [14–16]. Darüber hinaus hat Silicen den Vorteil, dass es besser mit bestehender elektronischer Technologie auf Siliziumbasis kompatibel ist. Diese Eigenschaften machen Silicen zu einem hervorragenden Material für die Nanoelektronik der nächsten Generation. Insbesondere ein Silicen-Feldeffekttransistor bei Raumtemperatur wurde im Experiment [17] erfolgreich durch einen Wachstumstransfer-Fertigungsprozess hergestellt.

Die Entdeckung von 2D-Dirac-Materialien bietet neue Möglichkeiten zur Erforschung der Quantenkontrolle des Tals. Die zwei ungleichen Täler K und K ^′ in der ersten Brillouin-Zone als zusätzlicher Freiheitsgrad neben Ladung und Spin für Quanteninformation und Quantenberechnung angesehen werden [18–20]. Beispielsweise kann der Valley-Freiheitsgrad eingebaut werden, um ein Elektronenspin-Qubit zu einem Spin-Valley-Qubit zu erweitern [18]. Daher hat die Valleytronics, die darauf abzielt, den Valley-Pseudospin zu erzeugen, zu detektieren und zu manipulieren, beträchtliches Interesse auf sich gezogen. In Graphen wurden verschiedene Schemata vorgeschlagen, um eine Talpolarisation zu erreichen, indem einzigartige Kantenmoden [21, 22], trigonaler Warping-Effekt [23], topologische Liniendefekte [24, 25], Dehnung [26, 27] und elektrostatische Gates verwendet werden [28]. Im Vergleich zu Graphen hat Silicen einen signifikanten Vorteil bei der Untersuchung von Valley Pseudospin. Es zeigt sich, dass Silicen unter der Modulation unterschiedlicher äußerer Felder eine reiche Vielfalt an topologischen Phasen und Chern-Zahlen aufweist [13, 16, 29, 30]. Bei Vorhandensein eines elektrischen Feldes E _z und Austauschfeld h , erforschte Ezawa das Phasendiagramm im E _z −h Ebene, die durch die Spin- und Valley-Indizes charakterisiert ist [16]. Unter weiterer Berücksichtigung des Rashba-SOI wird in Silicen aufgrund des topologischen Phasenübergangs ein tal-polarisierter quantenanomaler Hall-Zustand vorhergesagt [31]. Basierend auf dem Zustandsübergang wird ein Spinfilter auf Silicenbasis mit nahezu 100% Spinpolarisation vorgeschlagen, der robust gegenüber schwacher Unordnung ist [32]. Yokoyama untersuchte den ballistischen Transport durch einen ferromagnetischen (FM) Silicen-Übergang und zeigte einen kontrollierbaren Spin- und Valley-polarisierten Strom [33]. Bei Übergangsmetalldichalcogeniden mit gebrochener Inversionssymmetrie ist die Spinaufspaltung der Valenzbänder aufgrund intrinsischer SOI aufgrund einer Zeitumkehrsymmetrie an den beiden Tälern entgegengesetzt [3, 34, 35]. Die gebrochene Inversionssymmetrie könnte zu einer talabhängigen optischen Auswahlregel führen, die verwendet werden kann, um selektiv Träger im K . anzuregen oder K ^′ Tal über rechts bzw. links zirkular polarisiertes Licht [3, 34]. Im Experiment wurde das Signal der Talpolarisation durch optische [36, 37] und Transportmessungen [38, 39] untersucht. Ein riesiger nicht-lokaler Tal-Hall-Effekt wurde in Doppelschicht-Graphen beobachtet, der einem symmetriebrechenden elektrischen Gate-Feld ausgesetzt war, und das nicht-lokale Signal bleibt bis Raumtemperatur [38]. Eine aktuelle Übersicht über Valleytronics in 2D-Dirac-Materialien findet sich in Lit. [40].

Übergitter ist eine effektive Methode zum Engineering der elektronischen Struktur in Halbleitern und 2D-Materialien [41]. Übergittermuster mit Nanoskala können im Experiment natürlicherweise entstehen, wenn Graphen oder Silicen auf metallische Substrate aufgebracht wird [42, 43]. Ein Übergitter in Graphen könnte aufgrund der experimentell beobachteten chiralen Natur zu einer Renormierung der anisotropen Fermigeschwindigkeit [44] und zur Erzeugung neuer Dirac-Punkte im Spektrum [45–47] führen [43, 48, 49]. In Silicen-Übergittern mit elektrischem Feld E _z und Austauschfeld h , werden sowohl Spin- als auch Valley-Degenerationen aufgehoben. Es wird bestätigt, dass die Minibandstruktur und Minigaps, die durch die Übergitter verursacht werden, von den Spin- und Valley-Indizes abhängen [50]. Darüber hinaus konnten die Spin- und Talpolarisationen durch die Silicen-Übergitter verstärkt werden [51]. Wie bei Graphen werden viele neue elektronische Strukturen in Silicen-Übergittern erwartet. Es gibt jedoch nur sehr wenige Arbeiten zu Silicen-Übergittern [50, 51]. In diesem Beitrag diskutieren wir im Detail einen komplementären Aspekt, nämlich die spin- und talabhängige Bandstruktur und die Transporteigenschaft von Silicen. Wir fanden heraus, dass die Spin- und Valley-Indizes unterschiedliche Auswirkungen auf die zusätzlichen Dirac-Punkte und die anisotrope Geschwindigkeit haben, die durch die strukturellen Parameter eingestellt werden können. Die Geschwindigkeit wird aufgrund des elektrischen Feldes und des Austauschfeldes stark unterdrückt. Es wird eine bemerkenswerte Spin- und Valley-Polarisation erreicht, die durch die Fehlordnung stark verstärkt werden kann.

Das Papier ist wie folgt aufgebaut. Im Abschnitt „Methoden“ stellen wir den theoretischen Formalismus und die Dispersionsrelation vor. Die numerischen Ergebnisse zur Bandstruktur, Spin- und Valley-polarisierten Transmissionen werden im Abschnitt „Ergebnisse und Diskussionen“ gezeigt. Schließlich schließen wir mit einer Zusammenfassung im Abschnitt "Schlussfolgerungen".

Methoden

In der Einteilchen-Näherung gehorcht die elektronische Struktur von Silicen in der Nähe von Dirac-Punkten einem effektiven Dirac-Hamiltonian. Das betrachtete System ist ein eindimensionales Silicen-Übergitter, das durch eine Reihe lokaler Potentialbarrieren U . gebildet wird , Felder austauschen h , und senkrechtes elektrisches Feld E _z . U , h , und E _z sind nur in den Barrierebereichen mit Barrierebreite d . vorhanden _b , während U =h =E _z =0 in den Wannenbereichen mit Wannenbreite d _w , wie in Abb. 1 gezeigt. Das Übergitter mit einem Kronig-Penney-Typ variiert nur entlang x Richtung und die Länge einer Einheit beträgt d =d _b +d _w . Ein ähnliches Modell wurde in Lit. diskutiert. [51, 52], die sich hauptsächlich auf den thermoelektrischen und elektronischen Transport konzentrieren und nicht auf die Bandstruktur und den Unordnungseffekt, die in dieser Arbeit untersucht wurden. Experimentell U kann durch die metallischen Tore erzeugt werden und h kann durch den magnetischen Proximity-Effekt mit FM-Isolatoren EuO [33] erzeugt werden, die periodisch auf der Silicenschicht abgeschieden werden (siehe Abb. 1). Das elektrische Feld E _z senkrecht zu Silicen angewendet kann ein gestaffeltes Untergitterpotential induzieren Δ _z =ℓ E _z , mit 2ℓ ≈0.46Å der vertikale Abstand von A und B Stellen der beiden Untergitter aufgrund der geknickten Struktur [16]. Daher können die elektronischen Zustände durch den Hamilton-Operator beschrieben werden,

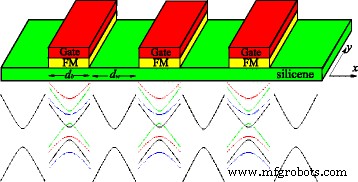
Oben:Schema der Silicen-Übergitter. Die FM-Isolatoren wie EuO und EuS auf der Oberseite von Silicen induzieren die Austauschfelder in Silicen, wie für Graphen vorgeschlagen [53]. Die metallischen Gates auf der Oberseite der FM-Isolatoren kontrollieren lokal das Fermi-Niveau. Unten:Schematische Darstellung des Energiespektrums in Silicen mit und ohne externe Felder

Δ _{η σ} =Δ _z −η σ λ _SO beschreibt die Bandlücke für verschiedene Spin- und Valley-Indizes, die durch das gestaffelte Potential gesteuert werden kann Δ _z und die SOI λ _SO . U _σ =U −σ h ist das effektive Potenzial für verschiedene Spin-Indizes. η =±1 bezeichnet das K und K ^′ Täler. σ =±1 bezeichnet Spin-Up- und Spin-Down-Zustände. v _F ist die Fermi-Geschwindigkeit. In Silicen sind die intrinsischen und extrinsischen Rashba-Effekte sehr gering und können vernachlässigt werden [15].

Aufgrund der Translationsinvarianz entlang des y Richtung, der Transversalwellenvektor k _y ist konserviert. Die Wellenfunktion für Tal η und drehe σ in jeder Region hat die Form Ψ (x ,y )=ψ (x )e ^iky _y mit

In den Barriereregionen ε _{η σ} =ε _b =(E −U _σ )+Δ _{η σ} und das x Komponente des Wellenvektors \(q_{\eta\sigma} =q_{b} =\sqrt {(E - U_{\sigma})^{2} - \Updelta ^{2}_{\eta\sigma} - (\hbar v_{F} k_{y})^{2}} / \hbar v_{F} \). In den Brunnenregionen ε _{η σ} =ε _w =E −η σ λ _SO und \(q_{\eta\sigma} =q_{w} =\sqrt {E^{2} - \lambda_{SO}^{2} - (\hbar v_{F} k_{y})^{ 2}} / \hbar v_{F} \). k _± =q _{η σ} ±i η k _y . Die Übertragungswahrscheinlichkeit T _{η σ} kann mit der Transfermatrixtechnik berechnet werden. Die normierte Leitfähigkeit für einen bestimmten Spin in einem bestimmten Tal bei der Temperatur Null ist gegeben durch

wo θ ist der Einfallswinkel bezüglich x Richtung. Die spin- und talaufgelösten Leitwerte sind definiert als \(G_{\uparrow (\downarrow)} =\left (G_{K \uparrow (\downarrow)} + G_{K^{\prime} \uparrow (\downarrow )} \right) / 2 \) und \(G_{K (K^{\prime})} =\left (G_{K (K^{\prime}) \uparrow} + G_{K (K^{ \prime }) \downarrow } \right) / 2\). Dann führen wir die Spinpolarisation P . ein _s und Talpolarisation P _v :

Basierend auf dem Satz von Bloch und der Stetigkeitsbedingung von Wellenfunktionen ist die Dispersionsrelation E (k _x ) für Spin-up- und Spin-down-Elektronen in der Nähe des K und K ^′ Täler können berechnet werden,

und k _x ist die Bloch-Wellenzahl. Zur Vereinfachung der Berechnung werden die dimensionslosen Einheiten eingeführt:\(E \rightarrow E d / \hbar v_{F}\), \(U \rightarrow U d / \hbar v_{F}\), \(\ Lambda _{SO} \rightarrow \lambda_{SO} d / \hbar v_{F}\), \(\Updelta _{z} \rightarrow \Updelta_{z} d / \hbar v_{F}\) , \(h \rightarrow hd / \hbar v_{F}\), k _y →k _y d , k _x →k _x d , d _w →d _w /d , und d _b →d _b /d . Beachten Sie, dass bei Δ _z =λ _SO =h =0, Gl. (6) wird auf dasjenige reduziert, das für lückenloses Graphen in einem periodischen Potential gefunden wird, bei dem sowohl Spin als auch Tal entartet sind [44–47]. Aus Gl. (6) sehen wir, dass das Austauschfeld h allein könnte die Spinspaltung bewirken, während das Tal die Entartung aufrechterhält. Die Talentartung kann jedoch durch das elektrische Feld E . aufgehoben werden _z mit Hilfe des SOI λ _SO . Somit könnte eine Kombination aus Austauschfeld und elektrischem Feld die Spin- und Tal-Entartungen anheben [16, 31–33], wie in Abb. 1 gezeigt. Im vorgeschlagenen System würden Elektronen mit unterschiedlichen Spins in der Nähe unterschiedlicher Täler verschiedene Band darstellen Strukturen und Transportfunktionen.

Ergebnisse und Diskussionen

In diesem Abschnitt würden wir die obigen Gleichungen verwenden, um die Bandstrukturen und Transporteigenschaften für verschiedene Spin- und Talindizes in Silicen-Übergittern zu berechnen. Die Breiten von Barrieren und Brunnen werden im Folgenden als gleich angenommen. Die Ergebnisse für den Fall mit ungleichen Well- und Barrierebreiten (d _b ≠d _w ) ähneln denen in lückenlosem Graphen [47]. Einige Parameter sind als d . festgelegt _b =d _w =50 nm und λ _SO =3,9 meV in Silicen, sofern nicht anders angegeben. Wir konzentrieren uns auf die ersten beiden Minibänder (die niedrigsten Valenz- und Leitungsminibänder) in der Nähe des Fermi-Niveaus.

Spin- und Valley-abhängige Bandstruktur

Erstens die Wirkung von potenziellem U auf Minibändern ist in Abb. 2 dargestellt. Um den Lückenfall und den lückenlosen Fall von Energiebändern gleichzeitig zu diskutieren, setzen wir Δ _z =7,8 meV=2λ _SO . Bei fehlendem Potenzial (U =0), das Spin-up-Elektron in der Nähe von K Tal (K ↑ Elektron) und Spin-Down-Elektron in der Nähe von K ^′ Tal (K ^′ ↓ Elektron) sind lückenlos (siehe Abb. 2 (a1, a4)), während das Spin-Down-Elektron in der Nähe von K Tal (K ↓ Elektron) und Spin-up-Elektron in der Nähe von K ^′ Tal (K ^′ ↑ Elektron) haben eine große Lücke (siehe Abb. 2 (a2, a3)). Die Minibänder der Spin-up-(oder Spin-down-)Elektronenverschiebung in den negativen (oder positiven) Energiebereich von E =0 um h , wegen des effektiven Potentials U _σ =U −σ h . Die Bandstrukturen von K ↑ (oder K ↓ ) Elektron und K ^′ ↓ (oder K ^′ ↑ ) Elektron spiegelsymmetrisch bezüglich E =0, im Einklang mit Gl. (6). Diese Spiegelsymmetrie wird jedoch in Gegenwart von U . zerstört . Beobachtbar, als U erhöht, erscheinen zusätzliche Dirac-Punkte, deren Anzahl sich zwischenzeitlich erhöht. Die zusätzlichen Dirac-Punkte können durch die Chiralität der Wellenfunktionen in ihrer Umgebung nachgewiesen werden [46]. Die Eigenschaften von Dirac-Punkten im Silicen-System hängen stark von den Spin- und Valley-Freiheitsgraden ab, wie in Abb. 2 gezeigt. Zum Beispiel bei U =135 meV in Abb. 2 (d1–d4) für K ↑ , K ↓ , K ^′ ↑ und K ^′ ↓ Elektronen, die Anzahl der Dirac-Punkte beträgt 5, 6, 4 bzw. 7. Für bestimmte Werte von U , wie zum Beispiel U =40,66 meV für K ↓ Elektron (siehe Abb. 2 (b2)) und U =100,63 meV für K ^′ ↑ Elektron (siehe Abb. 2 (c3)), kann ein neuer Dirac-Punkt bei k . erzeugt werden _y =0, und es wird sich in ein Paar aufspalten, das sich in entgegengesetzte Richtungen vom k . wegbewegt _y =0 Punkt, aber immer k _x =0, da U weiter erhöht. Folglich sind die Bandlücken für K ↓ und K ^′ ↑ Elektronen sind geschlossen (siehe Abb. 2 (b2, c3)) und das System mit Lücken wird lückenlos. Um den kritischen Wert von U . zu finden , wir setzen d _b =d _w und k _x =0. Analog zur Regel in lückenlosem Graphen [47] kann man unter Berücksichtigung des impliziten Funktionssatzes schließen, dass die Longitudinalwellenvektoren an den neuen Dirac-Punkten q _b =q _w wenn

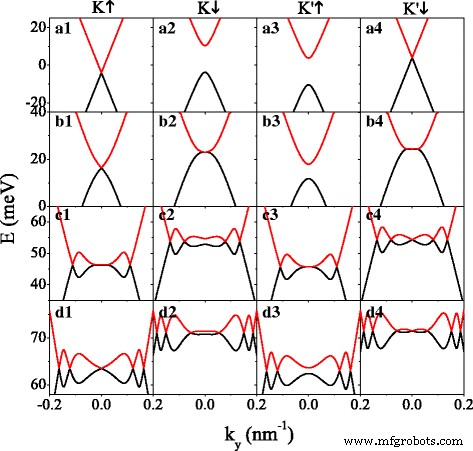
Energiespektrum im Vergleich zu k _y für mehrere verschiedene Potentialwerte U . (a1–a4) U =0; (b1–b4) U =40,66 meV; (c1–c4) U =100,63 meV; (d1–d4) U =135,0 meV. Die Parameterwerte sind h =8,0 meV, Δ _z =7,8 meV und k _x =0

Für K ↑ und K ^′ ↓ Elektronen mit η σ =1, wenn Δ _z =2λ _SO , Gl. (7) kann auf

Dementsprechend ist Gl. (6) wird zu

die erfüllt ist, wenn \(\left (\epsilon_{b}^{2} + \epsilon_{w}^{2}\right) q_{w}^{2} + (\epsilon_{b} - \epsilon _{w})^{2} k^{2}_{y} =-2 \epsilon _{w} \epsilon _{b} q_{w}^{2}\) oder q _w d =2n π (n ist eine positive ganze Zahl). Basierend auf Gl. (8), wir haben ε _b =−ε _w , und so ist die erste Gleichheit nur erfüllt, wenn k _{y 0} =0 für K ↑ und K ^′ ↓ Elektronen bei Δ _z =2λ _SO , entsprechend dem ursprünglichen Dirac-Punkt. Die Lösungen von q _w d =2n π haben die Form

Wenn \(\sqrt {E_{0}^{2}-\lambda_{SO}^{2}}d / 2\pi \hbar v_{F}\geq n\), k _{y 0} real ist, und es entstehen die neuen Dirac-Punkte, die genau bei (E ₀ ,k _{y 0} ). Bei niedrigen Werten von U , k _{y 0} ist imaginär und es gibt keine Lösung für n , was keine zusätzlichen Dirac-Punkte bedeutet. Die Dirac-Punkte erscheinen erst nach einem kritischen Wert von U , wie zum Beispiel U =40,66 meV für K ↓ Elektronen in Abb. 2 (b2), entsprechend n =1. Nach Gl. (10), Die Anzahl der Dirac-Punkte N _D erhalten werden kann. Wenn Δ _z =2λ _SO ,

für K ↑ und K ^′ ↓ Elektronen, während

für K ↓ und K ^′ ↑ Elektronen, wobei [...] einen ganzzahligen Teil bezeichnet. Beachten Sie, dass beim kritischen Wert von U , wie zum Beispiel U =40,66 meV und 100,63 meV, die Anzahl der Dirac-Punkte beträgt N _D =2n −1 für K ↓ und K ^′ ↑ Elektronen (siehe Abb. 2 (b2, c3)).

Gleichungen (7) und (10) zeigen, dass die Positionen und die Anzahl der Dirac-Punkte durch das elektrische Feld E . angepasst werden können _z und Austauschfeld h . Abbildung 3 zeigt die Anzahl der Dirac-Punkte N _D als Funktion von U für verschiedene Werte von E _z und h . Wenn Δ _z =7,8 meV in Abb. 3a, mit zunehmendem U , N _D für K ↑ und K ^′ ↓ Elektronen nimmt in ungerader Zahl zu, im Einklang mit Gl. (11). N _D für K ↓ und K ^′ ↑ Elektronen nimmt in Form einer geraden Zahl zu, im Einklang mit Gl. (12), außer N _D beim kritischen Wert. Ein Vergleich zwischen Abb. 3a und b zeigt, dass als h steigt, nimmt der kritische Wert für das Spin-down (oder Spin-up) Elektron allmählich ab (oder steigt). Wenn Δ _z =15 meV≠2λ _SO in Abb. 3c, N _D für alle Elektronen nimmt in gerader Zahl zu, außer N _D beim kritischen Wert. Die kritischen Werte von U sind für Elektron mit unterschiedlichen Spins und Tälern unterschiedlich. Die Dirac-Punkte könnten durch eine gemeinsame Modulation der Parameter U . gesteuert werden , E _z , und h .

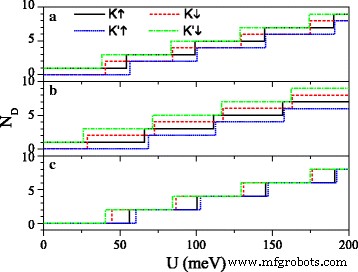
Anzahl Dirac-Punkte N _D gegen potenzielles U . (a ) h =8,0 meV und Δ _z =7,8 meV; (b ) h =20,0 meV und Δ _z =7,8 meV; (c ) h =8,0 meV und Δ _z =15.0 meV

Das Potenzial U und Barrierebreite d _b könnte verwendet werden, um die Bandlücke zu regulieren, wie in Abb. 4 dargestellt. Die Lücken für K ↑ und K ^′ ↓ Elektronen sind klein, während die Lücken für K ↓ und K ^′ ↑ Elektronen sind groß aufgrund von Δ _{η σ} =Δ _z −η σ λ _SO . Als U nimmt zu, alle Minibänder bewegen sich allmählich in Richtung des Hochenergiebereichs (siehe Abb. 4a) und alle Bandlücken zeigen eine gedämpfte Schwingung mit U (siehe Abb. 4b). Wenn U =σ h , das effektive Potential ist null und die Lücke erreicht den maximalen Wert. Die Lücke wird beim kritischen Wert von U . geschlossen , wegen der Entstehung neuer Dirac-Punkte. Abbildung 4c, d zeigt die Abhängigkeit von Minibändern und Bandlücken von der Barrierenbreite d _b bei U =0. Ohne externes Feld (d _b =0), die Minibänder bleiben entartet und die Lücke auf Fermi-Niveau beträgt 2λ _SO . Mit dem Erscheinen von d _b , wird das Miniband gespalten, wobei Valley und Spin nicht entartet werden. Die Minibänder von K ↑ (oder K ↓ ) und K ^′ ↓ (oder K ^′ ↑ ) Elektronen halten Spiegelsymmetrie um E =0 (siehe Abb. 4c). Als d _b nimmt zu, die Lücken von K ↓ und K ^′ ↑ Elektronen werden allmählich verbreitert. Die Lücken von K ↑ und K ^′ ↓ Elektronen sinken auf Null, wenn d _b erfüllt d _b /d _w =λ _SO /Δ _z , und danach mit d . erhöhen _b (siehe Abb. 4d). Die Spaltbreiten nähern sich der Sättigung mit der weiteren Zunahme von d _b . Darüber hinaus wird die Breite des Minibands auf d . verringert _b steigt (in der Abbildung nicht gezeigt) aufgrund der geringeren Kopplung von Eigenzuständen. Die Wirkung des elektrischen Felds auf die Bandlücke ist analog zu der in früheren Studien [50].

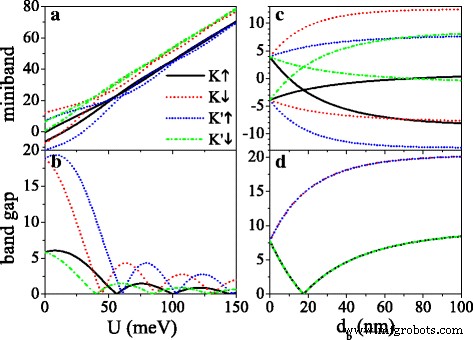
(a ) Minibänder in der Nähe des Fermi-Niveaus und (b ) ihre Bandlücken am ursprünglichen Dirac-Punkt gegenüber dem Potential U , um d _b =d _w =50 nm. (c ) Minibänder in der Nähe des Fermi-Niveaus und (d ) ihre Bandlücken am ursprünglichen Dirac-Punkt gegenüber d _b , bei U =0 und d _w =50 nm. Die Werte anderer Parameter sind h =8,0 meV, Δ _z =15,0 meV und k _x =k _y =0

Die Gruppengeschwindigkeit hängt stark von den Spin- und Valley-Indizes ab, wie in Abb. 5 gezeigt. Die Komponenten (v _x ,v _y ) der Geschwindigkeit kann definiert werden als

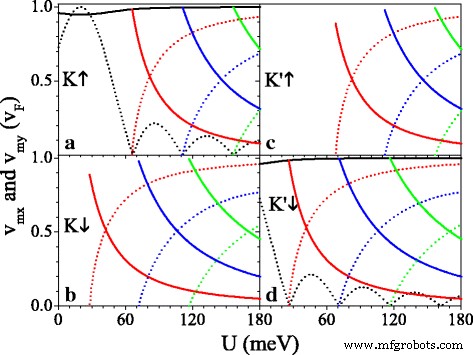
(a –d ) Geschwindigkeit versus Potential U , und die Parameter sind als h . eingestellt =20,0 meV und Δ _z =7,8 meV. Die schwarzen, roten, blauen und grünen durchgezogenen Kurven sind die Geschwindigkeiten v _0x , v _1x , v _2x , und v _3x , bzw. Die schwarzen, roten, blauen und grünen gestrichelten Kurven sind die Geschwindigkeiten v _0j , v _1j , v _2j , und v _3j , bzw.

Abbildung 5 zeigt die Geschwindigkeitskomponenten v _mx und v _mein in Einheiten von v _F am ursprünglichen Dirac-Punkt (m =0) und neue Dirac-Punkte (m =1,2,3). Das kann man als U . sehen erhöht, v _0j schwingt verfallen und v _0x v _F ist nahezu unbeeinflusst (siehe Abb. 5a, d). Beim kritischen Wert von U wo die neuen Dirac-Punkte auftauchen, v _mx v _F aber v _0j =v _mein =0, was auf ein Kollimationsverhalten entlang des k . hinweist _x Richtung für bestimmte Spins und Täler. Wenn U den kritischen Wert überschreitet und weiter ansteigt, v _mein auf v erhöhen _F aber v _mx allmählich auf Null sinken. Die Wirkung des periodischen Potentials ist aufgrund der chiralen Natur stark anisotrop. Die Eigenschaften der anisotropen Geschwindigkeit sind aufgrund der Lücke Δ . für verschiedene Spins und Täler unterschiedlich _{η σ} und das Potenzial U _σ , die mit U . kommandiert werden kann . Einnahme von U =20 meV zum Beispiel, v _0j =v _F für K ↑ Elektron ist viel größer als v _0j =0,16v _F für K ^′ ↓ Elektron und kein v _0j für K ↓ und K ^′ ↑ Elektronen aufgrund der Bandlücke. v _mx (oder v _mein ) für Spin-up-Elektronen ist immer größer (oder kleiner) als für Spin-down-Elektronen im gleichen Tal. Insbesondere impliziert Abb. 5 auch, dass für einen kleinen Wert von U , v _0x , v _0j , und v _mx kleiner als v . sind _F wegen Δ _z und h , anders als das lückenlose System [44]. Zum Beispiel v _1x =0,98v _F , 0,89v _F , 0,89v _F , und 0,98v _F für K ↑ , K ↓ , K ^′ ↑ und K ^′ ↓ Elektronen, wenn der Dirac-Punkt erscheint. Um den Einfluss von Δ . zu beleuchten _z und h auf die Gruppengeschwindigkeit zeigt Abb. 6 die Geschwindigkeiten (v _0x ,v _0j ) als Funktion von (a) Δ _z und (b) h für K ↑ Elektron. Aus Abb. 6a können wir deutlich erkennen, dass v _0x ist monoton fallend mit Δ _z während v _0j ist unempfindlich gegenüber der Änderung von Δ _z . Im Gegenteil, v _0x ist desensibilisiert gegen h , während v _0j steigt auf Maximalwert v _0j =v _F um h =σ U und nimmt dann mit h . ab . Die Ergebnisse zeigen, dass die Gruppengeschwindigkeit durch Δ . unterdrückt werden kann _z und h in Silikon.

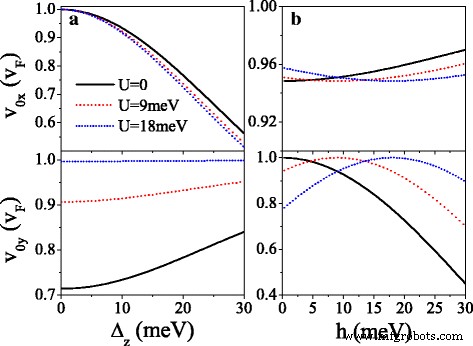
Geschwindigkeiten v _0x und v _0j gegen (a ) Δ _z und (b ) h , für K ↑ Elektron. (a ) h =20,0 meV und λ _SO =Δ _z /2. (b ) Δ _z =7,8 meV

Spin- und Valley-polarisierter Transport

Die spin- und talabhängige Bandstruktur spiegelt sich in der Transporteigenschaft wider und bietet eine Orientierungshilfe bei der Steuerung des Transports. In diesem Abschnitt diskutieren wir die Eigenschaften des spin- und talpolarisierten Transports durch ein endliches Silicen-Übergitter. Abbildung 7 zeigt die Übertragungswahrscheinlichkeit T _{η σ} für (a, c) K ↑ und (b, d) K ↓ Elektronen und die Periodenzahl n =10. Die rot gestrichelten Kurven sind die Minibänder, die auch die Grenzen für verschiedene elektronische Zustände sind, die die Übertragung bestimmen. Wir können sehen, dass die Übertragung im Minibandbereich eingeschränkt ist und keine Übertragung im Bandlückenbereich (siehe Abb. 7a, b). Die Transmissionsverteilung ist symmetrisch um k _y =0 wegen der symmetrischen Minibänder. Die Resonanzcharakteristik der Übertragung ergibt sich aus den Resonanzzuständen. Es sollte beachtet werden, dass die Übertragung immer noch in der Lückenregion in der Nähe von k . existiert _y =0 aufgrund des Tunneleffekts der Eigenzustände. T _{η σ} auf Fermi-Niveau für K ↑ und K ↓ Elektronen sind in Abb. 7c bzw. d) gezeigt. Man sieht deutlich, dass viele dünne Resonanzpeaks mit T _{η σ} =1 treten genau an den Positionen der Dirac-Punkte auf, was eine Anwendung des Systems als Spin- und Valley-Filter nahelegt.

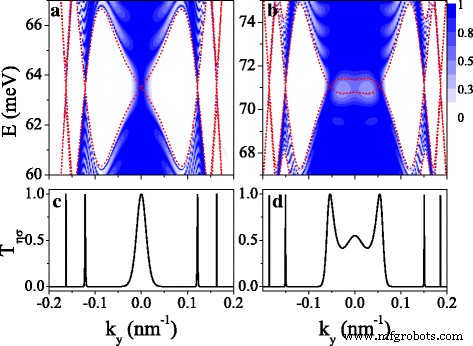
Konturdiagramm der Übertragung T _{η σ} (E ,k _y ) für (a ), (c ) K ↑ Elektron und (b ), (d ) K ↓ Elektron. Die Parameterwerte sind dieselben wie in Abb. 2 (d1–d4) und n =10

Die starke Abhängigkeit der Bandstruktur von den Spin- und Valley-Indizes ist für die Realisierung hoher Spin- und Valley-Polarisationen von Vorteil. Abbildung 8 zeigt die Minibänder, Leitwerte G _{η σ} , Spinpolarisation P _s , und Talpolarisation P _v als Funktion des Potentials U . It can be found that the distribution of conductance is completely in agreement with the band structure, that is, the conductance (or conductance gap) corresponds to the miniband (or band gap). The minibands for spin-up and spin-down electrons could be alternative distribution by adjusting h properly. Consequently, \(G_{K(K^{\prime })\uparrow }\) and \(G_{K(K^{\prime })\downarrow }\) present alternative distribution as well, i.e., \(G_{K(K^{\prime })\uparrow }\) nearly vanishes for those regions where \(G_{K(K^{\prime })\downarrow }\) is in resonance and vice versa. This result directly leads to a remarkable spin polarization, proposing a switching effect of spin polarization (see Fig. 8a). By changing Δ _z , the minibands and conductances for electrons near K and K ^′ valleys could be controlled, leading to a fully valley-polarized current (see Fig. 8b). Compared with spin polarization, the valley polarization is not perfect enough. However, this drawback could be remedied via the disorder structure of the system, as discussed in the following.

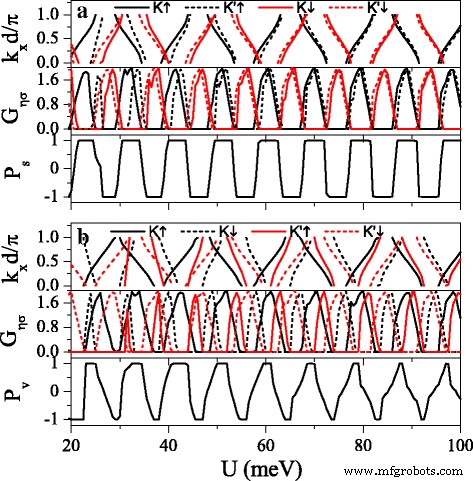
Minibands, conductances G _{η σ} , spin polarization P _s , and valley polarization P _v versus potential U . (a ) Δ _z =4.0 meV. (b ) Δ _z =12.0 meV. Other parameters are set as h =7.0 meV, E =6.0 meV, d _b =d _w =120 nm, and n =10

Figure 9 shows the (a) spin polarization P _s and (b) valley polarization P _v in (U ,h ) space. Interestingly, both P _s and P _v present periodical changes in the considered region, which is not observed in the ferromagnetic silicene junction [33]. Both distributions of P _s and P _v are antisymmetric with respect to h →−h . It is possible to achieve independently a full spin and valley polarization by a proper tuning of the fields U und h . For example, when h =6 meV and U =42 meV, P _s ≈1 and P _v ≈1, meaning that the current is mainly contributed by K ↑ electrons. When h =6 meV and U =44 meV, P _s ≈1 and P _v ≈−1 while P _s ≈−1 and P _v ≈−1 at h =6 meV and U =46 meV. The results demonstrate that a spin and valley polarization can be switched effectively.

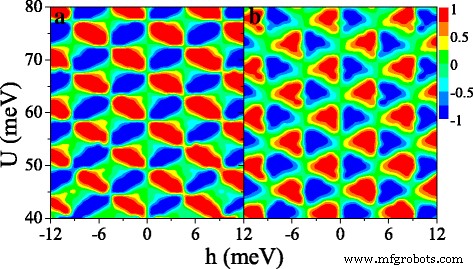
Contour plot of (a ) spin polarization P _s (U ,h ) und (b ) valley polarization P _v (U ,h ), at Δ _z =10.0 meV. The values of other parameters are the same as these in Fig. 8

In experiment, the structural imperfection of the model is unavoidable due to the limitations of the experimental techniques. Therefore, it is necessary to discuss the effect of the disorder on transmission. When the electric field or exchange field presents disorder, the conductance, spin polarization, and valley polarization are shown in Figs. 10 and 11. We set disorder situations of Δ _z und h fluctuate around their mean values, given by 〈Δ _z 〉=Δ _{z 0} and 〈h 〉=h ₀ , bzw. The fluctuations are given by

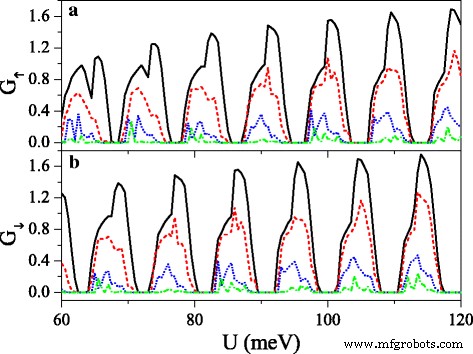
Conductances (a ) G _↑ and (b ) G _↓ versus potential U , when the electric field presents disorder, at n =50 and Δ _{z 0} =20.0 meV. The solid, dashed, dotted, and dash-dotted curves correspond to the disorder strength δ =0.0, 0.1, 0.3, and 0.6, respectively. The values of other parameters are the same as these in Fig. 8

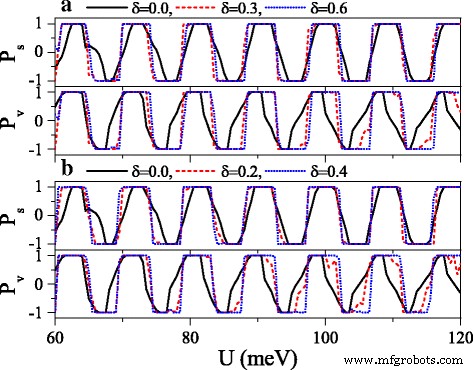
Polarizations P _s and P _v versus potential U when a the electric field or b the exchange field presents disorder. Δ _{z 0} =20.0 meV and h =7.0 meV in (a ). Δ _z =20.0 meV and h ₀ =7.0 meV in (b ). The values of other parameters are the same as these in Fig. 10

where {ζ _ich } is a set of uncorrelated random variables or white noise, − 1<ζ _ich <1, δ is the disorder strength, and i is the site index. Note that the disorder only takes place in the x direction, and the system is always homogeneous in y Richtung. Thus, k _y still keeps conservation. Figure 10 exhibits the effect of the disorder of the electric field on the conductances (a) G _↑ and (b) G _↓ . With the presence and increase of the disorder strength δ , both G _↑ and G _↓ are suppressed gradually, and each resonant peak splits into many small peaks. One may find that the conductance range is narrowed while the conductance gap range is broadened. Hence, the allowable (or forbidden) ranges of G _↑ completely fall into the forbidden (or allowable) ranges of G _↓ , giving rise to an excellent spin polarization (see Fig. 11). Furthermore, the positions of conductances and conductance gaps are nearly invariable as δ changes, suggesting that the miniband and band gap are insensitive to the disorder. Note that the disorder effect of the electric field on G _K and G _K ^′ is similar to that observed in Fig. 10. Figure 11 presents the disorder effects of (a) the electric field and (b) the exchange field on polarizations P _s and P _v . Obviously, with the increase of δ , P _s and P _v increase greatly, and the polarization platform is broadened. Thus, a full spin and valley polarization is realized. Comparison between Fig. 11a and b indicates that the disorder effect of exchange field is more prominent. The results demonstrate that the disorder could enhance the spin and valley polarizations compared with the order case, which is an advantage in realistic application.

Schlussfolgerungen

In summary, we demonstrated detailedly that band structure and transport property of silicene under a periodic field strongly depend on the spin and valley degrees of freedom. The numerical results indicate that electrons with different spins and valleys have various characteristics in Dirac point, bang gap, and group velocity. In particular, owing to the electric field and exchange field, the anisotropic velocity is restrained, which displays a collimation behavior for specific spins and valleys. Therefore, the transmission presents strong spin- and valley-dependent feature, consistent with the band structure, resulting in a significant spin and valley polarizations. In addition, the disorder could greatly enhance the spin and valley polarizations. Finally, we hope these results can be conducive to the potential applications of the spin and valley indices.

Abkürzungen

2D:

Zweidimensional

FM:

Ferromagnetic

SOI:

Spin-orbit interaction