Elektronische Eigenschaften von schwarzen Phosphor-Nanobändern für Sessel, kantenmodifiziert durch die Übergangselemente V, Cr und Mn

Einführung

Die Entdeckung von Graphen [1, 2] hat einen Forschungsschub für zweidimensionale (2D) Kristallmaterialien ausgelöst [3,4,5,6]. In den letzten zehn Jahren wurden hexagonales Bornitrid, Übergangsmetalldichalkogenid, schwarzes Phosphoren und viele andere hergestellt oder vorhergesagt [7,8,9]. Diese 2D-Materialien können in einer Vielzahl von Bereichen eingesetzt werden, was nicht nur für die Erforschung neuer physikalischer Phänomene und Leistungen unter der 2D-Grenze wichtig ist, sondern auch für viele neue Anwendungen in elektronischen, spintronischen und optoelektronischen Geräten [10,11,12,13 ,14,15,16,17,18,19,20,21]. Darüber hinaus können einige Eigenschaften von zweidimensionalen Materialien verbessert werden, nachdem sie in eindimensionale (1D) Nanobänder zugeschnitten oder/und funktionalisiert wurden [22, 23]. Bei Feldeffekttransistoren aus von unten nach oben synthetisiertem Graphen-Nanoband wurde eine hervorragende Leistung beobachtet [24]. Schottky-barrierefreie Kontakte mit 2D-Halbleitern über Metallcarbid oder -nitrid, die durch O- oder OH-Gruppen funktionalisiert sind, wurden vorhergesagt [25]. Für hocheffiziente Solarzellen wurden kantenmodifizierte Phosphoren-Nanoflocken vorgeschlagen [26]. Atomare Defekte und Verunreinigungen können verwendet werden, um die elektronischen Eigenschaften für potenzielle Anwendungen im Magnetismus und in der Katalyse lokal zu modulieren [27,28,29]. Das Anlegen eines externen elektrischen Felds und Heterostrukturen kann die elektronischen Eigenschaften weiter erheblich manipulieren [30,31,32].

Unter diesen bekannten 2D-Materialien ist schwarzes Phosphoren eines der wenigen mit überlegenen mechanischen, elektrischen und optischen Eigenschaften für Geräteanwendungen. Seit der Herstellung von darauf basierenden Feldeffekttransistoren [9] stößt schwarzes Phosphoren immer mehr auf Interesse. Es ist ein direkter Halbleiter mit moderater Bandlücke (≈ 2 eV) und hoher Lochbeweglichkeit (≈ 1000 cm ² /(Vs)) [33,34,35], die ein enormes Anwendungspotenzial in den Bereichen Elektronik, Optoelektronik, Sensorik, Katalyse und Batterien aufweisen [36,37,38,39]. Ähnlich wie Graphen kann schwarzes Phosphoren entlang zweier typischer Richtungen in Zickzack-Phosphoren-Nanobänder (ZPNRs) oder Armlehnstuhl-Phosphoren-Nanobänder (APNRs) geschnitten werden [40,41,42]. Die First-Principles-Simulation hat gezeigt, dass eine Substitutionsdotierung von Übergangsmetallen leicht Magnetismus in Phosphoren für Spintronikanwendungen einführen kann [43]. Die durch Defekte verankerte Absorption von Übergangsmetallen könnte zu halbmetallischen und metallischen Phosphoren-Verbundsystemen führen [44]. Es wurde vorhergesagt, dass die Kantenmodifikation von Übergangsmetallen auch die elektronischen Eigenschaften von Zickzack-Phosphoren-Nanobändern stark modulieren kann [45]. Soweit wir wissen, wurden die Auswirkungen der TM-Passivierung auf APNRs jedoch noch nicht gut untersucht.

In diesem Artikel konzentrieren wir uns auf die Modulation der elektronischen Eigenschaften von APNRs, die durch die typischen Übergangsmetallelemente V, Cr und Mn funktionalisiert sind, da sie größere magnetische Momente einführen als die anderen. Die auf der Dichtefunktionaltheorie basierenden Simulationen zeigen, dass das Halbhalbleiterverhalten auftreten und durch ein transversales elektrisches Feld gesteuert werden kann. Darüber hinaus leistungsstarker Spin p-n Junction kann für spintronische Anwendungen entworfen werden [46].

Systeme und Computermethoden

Schwarzer Phosphor ist ein Schichtmaterial, bei dem die Atomschichten durch eine schwache Van-der-Waals-Kraft zwischen den Schichten zusammengestapelt sind, während die Atome in jeder Schicht durch starke kovalente Bindungen verbunden sind. Es kann leicht in Monolayer-Phosphorene abgezogen werden. Die Draufsicht eines Phosphorens ist in Abb. 1a mit einem Zoom-in-Teil auf der rechten Seite schematisch dargestellt, um die Geometrieparameter zu zeigen. Außerdem sind zwei Seitenansichten entlang der Sessel- bzw. Zickzackrichtung gegeben. Jedes Phosphoratom ist an drei benachbarte Phosphoratome (mit Gitterkonstanten 3,31 und 4,38 Å, Bindungslänge 2,2 Å, Bindungswinkel 96,34° und Diederwinkel 102,1°) gebunden, um eine gefaltete Wabenstruktur zu bilden [47]. Wie andere zweidimensionale Materialien eines hexagonalen Wabengitters wie Graphen und Molybdändisulfid kann ein Phosphoren auf Nanobänder mit zwei typischen Kantenmorphologien zugeschnitten werden, dem Sessel- und Zickzack-Schwarz-Phosphoren-Nanoband [40, 41, 48, 49].

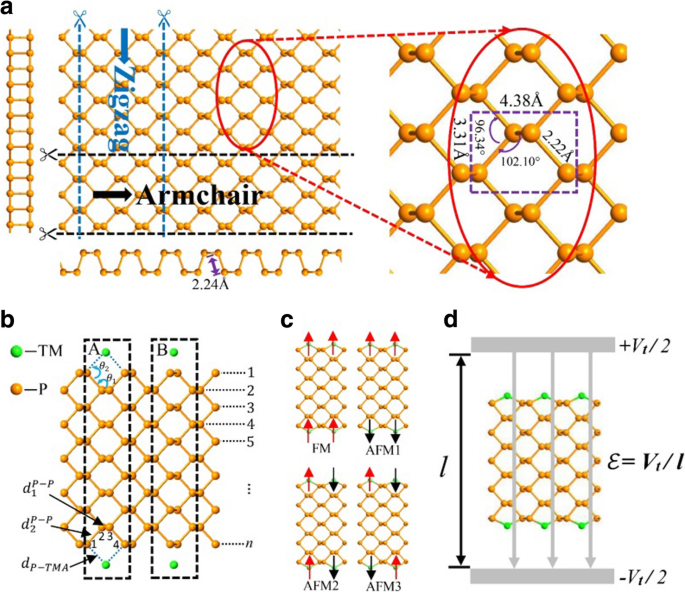
a Draufsicht und Seitenansicht eines 2D-Phosphorens mit einer Zoom-in-Ansicht auf der rechten Seite. Die Querschnittsansichten von den Sessel- und Zickzackkanten sind unten bzw. auf der linken Seite gezeigt. b Ein APNR mit TM-Adatomen an hohlen Stellen (A) und oberen Stellen (B) am Rand. Die gestrichelten Rahmen geben die Größe der primitiven Zelle und die Zahl n . an bezeichnet die Breite des Nanobandes. c Die vier magnetischen Konfigurationen von APNRs. d Das schematische Diagramm bei Vorhandensein eines transversalen elektrischen Felds

Hier betrachten wir den Halbleiter n -APNRs für ungerade Breitenzahl n mit spiegelsymmetrischem Querschnitt. Ähnliche Ergebnisse sollten sogar für n . folgen da die beiden Kanten des Nanobandes fast unabhängig sind, wie im Folgenden angesprochen wird. Die Auswirkungen von Kantenmodifikationen durch drei typische Übergangsmetall(TM)-Elemente V, Cr und Mn werden systematisch analysiert. Wie in 1b dargestellt, kann ein TM-Atom an einer APNR-Kante an der hohlen Position (Fall A) oder an der oberen Position (Fall B) adsorbiert werden. Da Fall A eine viel größere Bindungsenergie hat, nehmen wir ihn an, wo ein TM-Atom in der Nähe des Zentrums jeder hohlen Position adsorbiert wird und nebenbei an die beiden Phosphorkantenatome bindet. Um die Beschreibung der Bindungsgeometrie der TM-Atome an den APNR-Kanten zu erleichtern, wie in Abb. 1b dargestellt, bezeichnen wir die Phosphoratome an den Plätzen 1, 2, 3 und 4 als P₁ , P₂ , P₃ , und P₄ , bzw. Wir definieren auch einige Geometrieparameter:die Bindungslängen \( {d}_1^{P-P} \) (zwischen P₂ und P₃ ), \( {d}_2^{P-P} \) (zwischen P₁ , P₂ oder P₃ , P₄ ) und d ^{P − TM} und die Bindungswinkel θ ₁ (zwischen \( {d}_1^{P-P} \) und\( {d}_2^{P-P} \)) und θ ₂ (zwischen \( {d}_2^{P-P} \) und d ^{P − TM} ). Aufgrund des Magnetismus der TM-Adatome gibt es vier mögliche magnetische Konfigurationen, d. h. FM, AFM1, AFM2 und AFM3, wie in Abb. 1c gezeigt. In Abwesenheit eines Magnetfelds zeigt unsere Simulation, dass die Energie der AFM2-Elementarzelle in Abb. 1c etwa 0,2 eV niedriger ist als die der FM-Elementarzelle. Die beiden Kanten sind fast unabhängig, und die entgegengesetzte Spinpolarisation zwischen ihnen in den AFM1- und AFM3-Konfigurationen kann die Energie um einen Betrag von weniger als 0,002 eV reduzieren. In diesem Artikel untersuchen wir die elektronischen Eigenschaften der Nanobänder in der FM-Konfiguration, da ein angelegtes Magnetfeld sie möglicherweise halten kann. Wir untersuchen auch die Auswirkungen eines angelegten transversalen elektrischen Felds, wie in Abb. 1d dargestellt, auf die elektronische Struktur und die Eigenschaften von FM-APNRs. Schließlich schlagen wir mögliche Geräteanwendungen der Materialien vor.

Die Transporteigenschaften eines Nanoband-Übergangs werden berechnet, indem eine Zwei-Sonden-Bauelementstruktur erstellt wird. Der Übergang ist in drei Teile unterteilt:Ein Streubereich, in dem sich die Übergangsgrenzfläche befindet, liegt zwischen der linken (L) und der rechten (R) Elektrode. Bei einer Vorspannung von V _b zwischen den beiden Elektroden angelegt wird, setzen wir die Fermi-Energien in den Elektroden L und R als μ _L =  − e |V _b |/2 und μ _R = e |V _b |/2. Der elektronische Spinstrom σ durch die Quantenbauelemente wird durch die Landauer-Büttiker-Formel [50] ausgewertet:

Hier, T _σ (E ) ist die Spinübertragung σ und f die Fermi-Dirac-Verteilungsfunktion.

Die Simulation wird mit dem Atomistix Toolkits (ATK)-Paket durchgeführt, das auf der Ab-initio-Dichtefunktionaltheorie (DFT) in Kombination mit der Nichtgleichgewichts-Green-Funktion (NEGF)-Methode basiert [51, 52]. Vor der elektronischen Struktur- und Transportsimulation werden die Strukturen optimiert, bis die auf jedes Atom einwirkenden Kräfte kleiner als 0,02 eV/Å sind. Für das Austauschkorrelationsfunktional verwenden wir die spinabhängige generalisierte Gradienten-Approximation mit der Perdew-Burke-Emzerhof-Parametrisierung (SGGA-PBE). Wir haben bestätigt, dass SGGA+U-Simulationen zum gleichen Ergebnis führen wie im Folgenden dargestellt [43]. Ein Basissatz von doppelt zeta-polarisierten (dzp ) Atomorbitale werden in der Berechnung verwendet, um ein genaues Ergebnis zu erhalten. Zwischen benachbarten Nanobändern wird eine 20-Å-dicke Vakuumschicht eingefügt, um Kopplungen zwischen den Bändern zu vermeiden. Die Abschneideenergie für die Basisvektorentwicklung von Wellenfunktionen wird als 150 Hartree oder 4082 eV mit einem k . festgelegt -Raummaschengitter von 1 × 1 × 101. Eine elektronische Temperatur von 300 K wird in der Technik der Real-Achsen-Integration für das NEGF-Schema verwendet, um die Simulation zu erleichtern. Die vier magnetischen Konfigurationen werden durch anfängliches Einstellen der entsprechenden Spinpolarisationen der TM-Adatome vor der Optimierung erhalten. Das transversale elektrische Feld ε wird durch zwei parallele virtuelle Metallplatten erzeugt, die durch einen Abstand l . getrennt sind , mit einer elektrischen Potentialdifferenz V _t also ε =V _t /l .

Ergebnisse und Diskussion

Geometrie und Bindungsenergie

In unberührten APNRs verschieben sich die P-Atome der Kante in die hohle Position, sodass jeder Kanten-„Sessel“ im Vergleich zu ihrem 2D-Gegenstück schmaler wird, wie in Abb. 2a, b gezeigt. Wird ein APNR hydriert, wobei die schwebende Bindung jedes P-Kantenatoms mit einem H-Atom gesättigt ist, wie in Lit. [48, 53] kehren die P-Randatome in ihre 2D-Positionen zurück, wie in Abb. 2c dargestellt. Wenn an jeder hohlen Position ein TM-Atom adsorbiert ist, passiviert es die beiden P-Randatome daneben. Die Sessel erholen sich dann teilweise und die Kanten werden aufgrund der Spinpolarisation der TM-Adatome magnetisiert. In der FM-Konfiguration wird an den Kanten keine Rekonstruktion beobachtet und die Länge der primitiven Zelle bleibt unverändert, wie in Abb. 2d–f gezeigt.

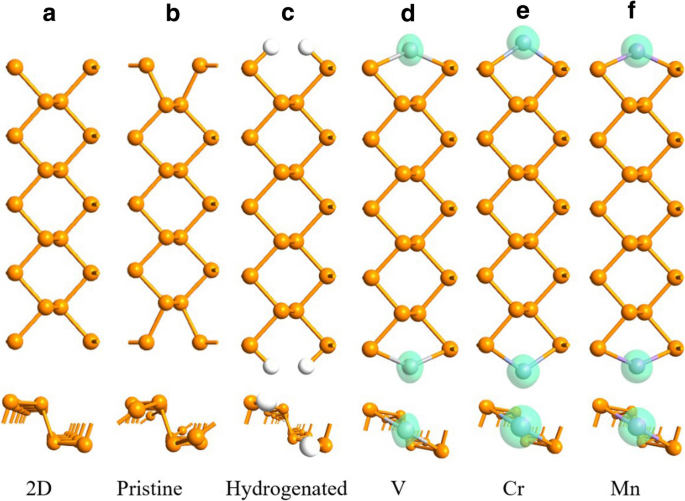
Geometrien von FM 9-APNRs a gerade aus einem 2D-Phosphoren geschnitten, b geometrisch optimiert (unberührt), c hydriert und nach Adsorption von d V, e Cr und f Mn-Atome am Rand. Die Dichte der Spinpolarisation der Atome wird durch die grüne Isofläche mit dem Wert 0,004 e/Å ³ . angezeigt

In Tabelle 1 listen wir die Geometrieparameter und die Bindungsenergie E . auf _b für reine, hydrierte und TM-adsorbierende 9- und 17-APNRs in der FM-Konfiguration, falls zutreffend. Hier, E _b = (mE _X + E _APNR − E _{X − APNR} )/m mit E _X , E _APNR , und E _{X − APNR} die Gesamtenergien eines externen Atoms, einer primitiven Zelle aus reinem APNR und einer primitiven Zelle aus APNR passiviert durch m externe Atome jeweils mit m =4 für H und m =2 für TM-Elemente. Wenn wir ein 2D-Phosphoren schneiden, um ein APNR herzustellen, reduzieren sich die hängenden Bindungen an den Kanten erheblich θ ₁ von 102 bis 87°. Die Passivierung der suspendierten Bindungen durch externe Atome erholt sich θ ₁ und führt eine abstoßende Reaktion ein, gekennzeichnet durch die Dehnung von \( {d}_{P-P}^1 \) und \( {d}_{P-P}^2 \). In den TM-Fällen zeigt die Adsorption von V-Atomen die stärkste abstoßende Reaktion mit der größten θ ₁ . Ähnlich wie bei H ist die Adsorption des TM-Elements mit einer Bindungsenergie in der Größenordnung von 4 eV energetisch stabil. Die beiden Kanten von APNRs sind fast unabhängig voneinander, daher sind die Geometrieparameter und E _b sind unempfindlich gegenüber der Breite von APNR. Die Bindungsgeometrie und Energie halten auch in verschiedenen magnetischen Konfigurationen für TM-n -APNRs.

Elektronische Struktur und magnetische Eigenschaften

In Abb. 3 präsentieren wir die Bandstrukturen und typischen Wellenfunktionen von Elektronen in 9-APNRs mit und ohne Kantenmodifikation. Unberührte APNRs sind nichtmagnetische indirekte Halbleiter mit einer Bandlücke von E _g ≈ 0.5 eV, wobei die elektronischen Zustände am oberen Ende des Valenzbandes (Leitung) (unten) Volumenzustände (Kanten) sind. Wenn die P-Kantenatome durch H-Atome passiviert werden, verschiebt sich das Leitungsband aufgrund von kantenaufhängenden Bindungen in unberührten APNRs weg von der Bandlücke und die hydrierten ANPRs werden zu direkten Halbleitern mit einer breiteren Bandlücke von E _g ≈ 1.0 eV. Die Zustände am unteren Ende des Leitungsbandes und am oberen Ende des Valenzbandes sind alle Bulk-Zustände. Mit zunehmender Breite von n =9 bis 17, nimmt die Bandlücke geringfügig von 1,01 auf 0,89 eV in Übereinstimmung mit den von Han et al. vorhergesagten ab. [49].

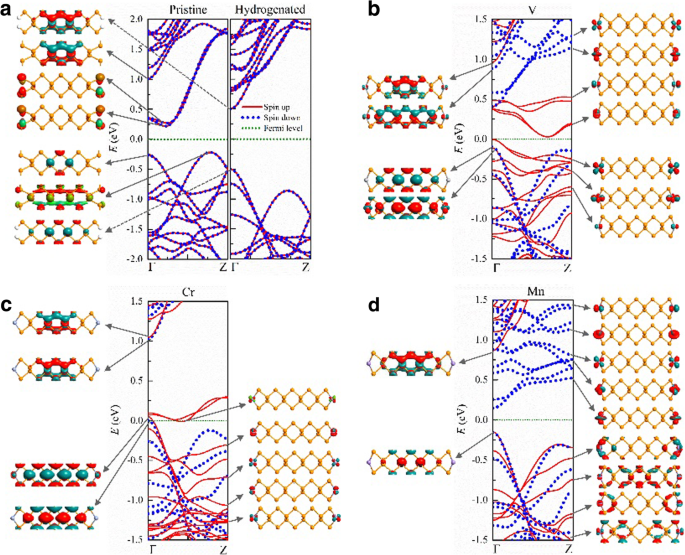
Bandstrukturen und typische Wellenfunktionen nahe der Fermi-Energie von unberührten 9-APNRs kantenmodifiziert durch a H, b V, c Cr und d Mn-Atome

Wenn TM-Atome an den Kanten von APNRs adsorbiert werden, bleiben sie spinpolarisiert. In der FM-Konfiguration V-n -APNRs sind magnetische Halbleiter mit spinabhängiger Bandlücke. Wie in Abb. 3b dargestellt, für n =9, haben die Spin-up-Elektronen eine indirekte Lücke von \( {E}_g^{\mathrm{up}}\approx 0,03 \) eV, während die Spin-down-Elektronen eine direkte Lücke von \( {E}_g ^{\mathrm{down}}\approx 0.5\) eV. Die elektronischen Zustände in den Spin-up-Bändern um die Fermi-Energie setzen sich zusammen aus d Orbitale der V-Adatome und sind auf Kanten beschränkt. Diese Spin-up-Kantenbänder haben eine ähnliche Dispersion und sind teilweise besetzt. Das entsprechende Valenzband oben und das untere Leitungsband trennen sich im k Raum, sind aber energetisch nahe beieinander. Für Spin-up-Elektronen tritt eine schmale indirekte Bandlücke auf. Im Gegensatz dazu liegen alle Spin-Down-Kantenbänder weit über der Fermi-Energie. Das Spin-Down-Valenzband stammt von Volumenzuständen und weist eine entgegengesetzte Dispersion des Spin-Down-Leitungsbandes auf, das von Randzuständen stammt. Daraus ergibt sich die direkte Bandlücke für Spin-Down-Elektronen. Die V-Kantenbänder erscheinen aufgrund der schwachen Kopplung zwischen den linken und rechten V-Kantenatomen paarweise. Drei der fünf Paare sind besetzt, sodass jede primitive Zelle ein magnetisches Moment von 6 μ . hat _B .

Ein Spin-Up-Paar und alle Spin-Downs d Orbitalkantenbänder befinden sich oberhalb des Fermi-Niveaus in Cr-9-APNR, wie in Abb. 3c dargestellt, da es vier d Orbitalelektronen in jedem Cr-Atom. Aufgrund der leichten Überlappung der beiden höchsten Paare von Spin-Up-Kantenbändern in der Nähe des oberen Spin-down-Valenzbandes wird es zu einem Halbmetall mit dem Fermi-Niveau knapp über dem oberen Rand des Spin-down-Valenzbandes. In Mn-9-APNR sind alle fünf Spin-up-Paare d Orbitalbänder sind während des Spindowns besetzt d Orbitalbänder sind leer, wie in Fig. 3d gezeigt. Es wird ein halber Halbleiter, bei dem sich die Bandlücken entgegengesetzter Spins stark unterscheiden, mit \( {E}_g^{\mathrm{up}}\approx 1 \) eV für Spin-up und \( {E}_g^{\ mathrm{down}}\approx 0.3 \) eV für Spin-Down. Beide Spins haben die gleiche Valenzbandspitze, auf der sich Volumenzustände befinden. Aufgrund der unbesetzten Spin-Down-Kantenzustände ist die Leitungsbandunterseite des Spin-Down jedoch viel niedriger als die des Spin-Up.

Die elektronischen Strukturen von TM-n -APNRs bleiben das gleiche Muster und ändern sich nicht viel wie n steigt, wie in Abb. 4 dargestellt. Dennoch können die physikalischen Eigenschaften in den Cr-passivierten Proben erheblich variieren, da sich eine Energielücke als n . öffnen kann steigt. Schmaler Cr-n -APNRs sind halb aus Metall, aber breite Cr-n -APNRs können zu Halbleitern werden, wie in den Einfügungen von Abb. 4 für n . gezeigt =11 und n =17 bzw..

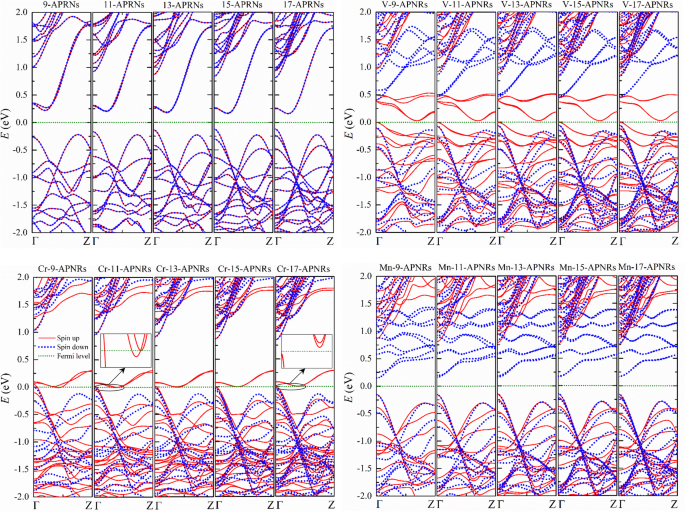
Bandstrukturen von unberührten n -APNRs und solche mit V-, Cr- und Mn-Atomen für verschiedene n . Vergrößerte Ansichten von Cr-n -APNRs in der Nähe des Fermi-Niveaus werden in den Einschübe für n . angezeigt =11 und 17

Die magnetischen Momentverteilungsprofile von FM TM-9-APNRs sind in Abb. 2 gezeigt, wo die Isoflächen der Spindichte ∆ρ = ρ ^hoch − ρ ^unten = 0,004 e/Å ³ sind geplottet. Hier, ρ ^hoch und ρ ^unten sind die Dichten der Spin-up- bzw. Spin-down-Elektronen. Die magnetischen Momente konzentrieren sich hauptsächlich um die TM-Atome, und der Beitrag der P-Atome ist zu klein, um klar gezeigt zu werden. In Tabelle 2 präsentieren wir das gesamte magnetische Moment M _T in einer primitiven Zelle die Momentensumme der zehn Kantenatome M _E =2 M (TM) + 4 M (P₁ ) + 4 M (P₂ ) und das Moment eines Einzelkantenatoms TM, P₁ /P₄ , oder P₂ /P₃ .

Die gesamten magnetischen Momente stammen hauptsächlich von den Randatomen (M _T ≈ M _E ) und in der Einheit μ _B pro primitiver Zelle liegen nahe bei den Valenzelektronenzahlen der Übergangsmetallatome minus 4. In V-n -APNRs, die Rand-P-Atome (P₁ und P₄ ) sind leicht antiparallel polarisiert, während die P-Atome der zweiten Kante (P₂ und P₃ ) sind parallel polarisiert. Damit heben sich die magnetischen Momente der P-Atome nahezu auf. Jedes V-Atom hat ein magnetisches Moment von etwa 3 μ _B von drei 3d Orbitale. Die 4s Orbital ist ähnlich wie ein einzelnes V-Atom voll besetzt. Im Gegensatz dazu sind die Rand-P-Atome in Cr-n -APNRs haben viel größere magnetische Momente von M (P1) ≈  − 0,27μ _B . Zufälligerweise haben sie die längsten d ^{P − TM} unter den drei TM-APNRs, was auch die größte Geometrieabweichung der P-Atome von denen in 2D-Phosphoren anzeigt. Darüber hinaus hat jedes Cr-Atom ein magnetisches Moment von ungefähr 5 μ _B , statt 4 μ _B . Dies deutet darauf hin, dass seine 4s Orbital ist nicht vollständig besetzt und trägt zur Spinpolarisation bei, ähnlich wie im Fall eines isolierten Cr-Atoms mit einer Valenzelektronenkonfiguration von 3d ⁵ 4s ¹ . Die spinpolarisierten s Orbitale von Cr-Atomen in Cr-APNRs könnten die antiparallele Spinpolarisation im p . induzierten Orbitale in ihren benachbarten P-Atomen über den kinetischen Austauschmechanismus. In Mn-n -APNR, das d Orbitale des Mn-Atoms sind halb besetzt mit einem magnetischen Moment von etwa 5 μ _B und die benachbarten P-Atome sind alle sehr schwach parallel polarisiert. In Abb. 5 zeichnen wir die partielle Zustandsdichte (PDOS) (blau) von d Orbitale in TM-Atomen zusammen mit der Gesamtzustandsdichte (DOS) (schwarz) von 9-APNRs. Hier der Spinsplit und die Energiespreizung von d Orbitale werden deutlich angezeigt. In reinen und hydrierten APNRs überlappen Spin-up- und Spin-down-DOS-Spektren miteinander, was auf keine Spinpolarisation hindeutet. In TM-APNRs sind das Spin-Up und das Spin-Down d Orbital-PDOS-Spektren verteilen sich hauptsächlich in einem Energiebereich von 2 bis 4 eV. Sie sind energetisch gut getrennt mit einem Abstand von etwa 3, 9 und 4 eV in V-, Cr- bzw. Mn-APNR. Ausgenommen der d Orbitale, die p Orbitale von P-Atomen dominieren den Beitrag zur DOS der Valenzbänder. Beachten Sie, dass die s Orbitale von Cr-Atomen tragen ebenfalls signifikant zu Cr-APNRs bei. Die Kantenpassivierung von Co- und Ni-Atomen kann auch Magnetismus in APNRs einführen, aber der Magnetismus, der durch andere TM-Elemente wie Sc, Ti, Fe, Cu und Zn eingeführt wird, könnte ziemlich begrenzt sein.

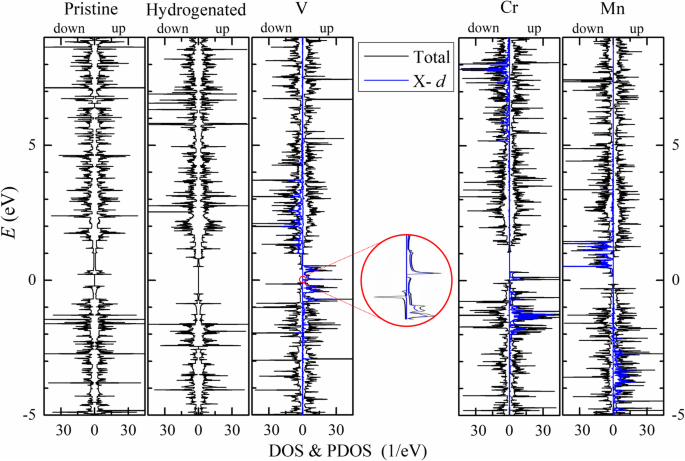
Die DOS (schwarze Kurve) von unberührten und modifizierten 9-APNRs in ihrem FM-Zustand ist für den Aufwärtsspin (rechts) und den Abwärtsspin (links) aufgetragen. Die d Orbital-PDOS (blaue Kurve) von TM-Atomen ist ebenfalls zum Vergleich dargestellt. Die DOS von V-9-APNR nahe der Fermi-Energie ist in den Einschub gezoomt, um die Bandlücke zu zeigen

Auswirkungen eines elektrischen Querfeldes

Transversale elektrische Felder wurden in elektronischen Geräten häufig verwendet, um die Ladungsträgerkonzentration und die Bandstruktur von Halbleitern zu steuern [54, 55]. Wie in Abb. 1d angedeutet, simulieren wir die elektronischen Strukturen von TM-n -APNRs in der FM-Konfiguration unter einem transversalen elektrischen Feld \( \mathcal{E}={V}_t/l \) parallel zur Nanobandebene, über Sandwich-Nanobänder zwischen zwei parallelen Balken. Hier, V _t ist die Spannungsdifferenz zwischen den beiden Balken und l ist die Trennung zwischen ihnen. Aufgrund des Stark-Effekts sollten sich zwei entartete Zustände, die im realen Raum um einen Abstand Δ entlang des elektrischen Feldes getrennt sind, um einen Betrag von \(\delta E=e{\mathcal{E}}^{\ast}\Delta\) teilen , wobei das wirksame elektrische Feld \({\mathcal{E}}^{\ast}\) infolge des Abschirmeffekts in der Regel kleiner ist als das äußere elektrische Feld \(\mathcal{E}\). In TM-n -APNRs kann der Abstand Δ zwischen den Zustandszentren eines Kantenbandpaares so groß wie die Nanobandbreite sein, wenn jeder Zustand nur auf eine Kante beschränkt ist, aber Δ sollte bei gemischten Kantenzuständen kürzer sein oder sogar verschwinden. Wie die Wellenfunktionen in Abb. 3 zeigen, sind die Kantenzustände normalerweise gemischt.

In Abb. 6 präsentieren wir die Bandstrukturen von V-, Cr- und Mn-13-APNR für verschiedene \(\mathcal{E}\). Die Nanobandbreite beträgt ungefähr \( w=0.5\left(n-1\right)\times 3,31\ {\AA}+{d}^{P-\mathrm{TM}}\cos \left({135}^ {{}^{\circ}}-{\theta}_2\right)\approx 21\kern0.20em {\AA}.\)Die Stark-Aufspaltung ist viel kleiner als \(e\mathcal{E}w\) zeigt einen starken Abschirmeffekt oder eine starke Mischung der Randzustände an. Da V-13-APNR eine sehr schmale Spin-up-Bandlücke hat, wird es bei etwa \(\mathcal{E}=3\) V/nm halbmetallisch. Die Stark-Aufspaltung von Leitungskantenbändern kann bei \(\mathcal{E}=5\) V/nm bis zu 0.1 eV betragen. Cr-13-APNR zeigt eine ähnliche Stärke der Stark-Aufspaltung und bleibt unter dem transversalen Feld halbmetallisch.

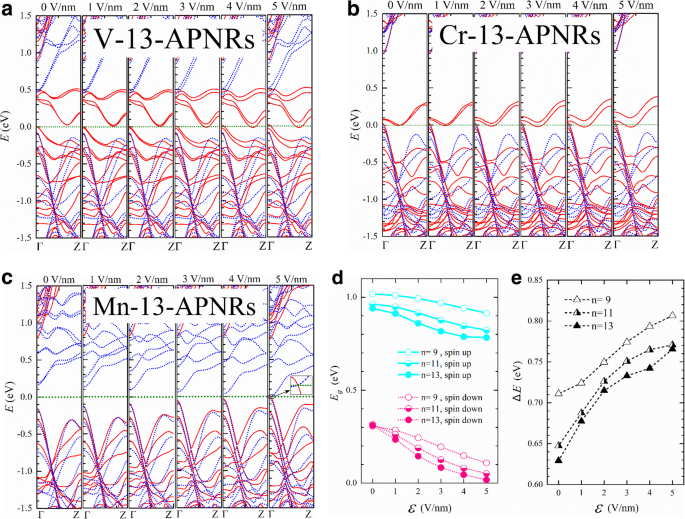
Die Spin-up (durchgezogen) und Spin-down (gestrichelt) Bandstrukturen von a V-, b Cr- und c Mn-13-APNRs unter einem transversalen elektrischen Feld der Stärke \(\mathcal{E}=0,1,\dots, 5\) V/nm. d Die Bandlücken von Mn-n -APNRs versus \(\mathcal{E}\) für Upspin (\({E}_g^{\mathrm{up}}\), durchgezogene Linien) und Downspin (\({E}_g^{\mathrm {down}} \), gepunktete Linien) mit n =9, 11 und 13. e Die Lückendifferenz \(\Delta E={E}_g^{\mathrm{up}}-{E}_g^{\mathrm{down}}\) gegen \(\mathcal{E}\)

Ein viel stärkerer Stark-Effekt wird beim Halbhalbleiter Mn-13-APNR beobachtet, wie in Fig. 6c gezeigt. Die Spin-Down-Leitungsbandpaare von Kantenzuständen erhalten am Γ-Punkt in k . eine Aufspaltung von etwa 0.55 eV Raum unter \(\mathcal{E}=5\) V/nm. Das Spin-down-Leitungsband überlappt mit dem Spin-up-Valenzband, und das Mn-13-APNR geht von einem halben Halbleiter zu einem Metall über, wie durch den vergrößerten Einschub dargestellt. In Fig. 6d tragen wir die Spin-Up- und Spin-Down-Energielücken gegen die Feldstärke auf. Die Elektronenwellenfunktionen ändern sich mit dem Feld, und die Energielücken ändern sich nicht linear mit dem Feld. Die Bandlücke von Mn-13-APNRs verschwindet bei \(\mathcal{E}=5\) V/nm für Spin-Down-Elektronen fast, bleibt aber über 0,75 eV für Spin-Up-Elektronen. Die Energielückendifferenz ∆E zwischen den entgegengesetzten Spins ist in Abb. 6e gegen \(\mathcal{E}\) aufgetragen für n =9, 11 und 13. ∆E steigt in einem viel langsameren Schritt für n =9 als für n =11 und 13 im unteren Halbbild, aber die Art und Weise kehrt sich im hohen Halbbild um.

Drehen p-n Kreuzung

Wir haben gesehen, dass TM-Atome die Bandstruktur von APNRs auf verschiedene Weise modulieren können. Dies bietet Möglichkeiten für ein neuartiges Gerätedesign. Zum Beispiel können wir Cr-APNRs und Mn-APNRs kombinieren, um ein spinabhängiges p-n . zu bilden Kreuzung. Experimentell ist die Metallionendotierung [56] in Phosphoren verfügbar. Auch das glatte Stitching von 2D-Materialien [57] und die atomare Kantenmodifikation von Nanobändern sind realisierbar [58]. Diese Techniken könnten verwendet werden, um das p-n . herzustellen Kreuzung. In Abb. 7a tragen wir seine Strom-Spannung (I-V ) Kennlinie, die aus der Simulation des im oberen Einschub gezeigten Zwei-Sonden-Systems erhalten wurde. Der Spin p-n Übergang zeigt einen sehr starken Gleichrichtungseffekt für Spin-up-Elektronen, aber nur einen schwachen Effekt für Spin-down-Elektronen. Diese Spinabhängigkeit kommt von den ausgeprägten Bandstrukturen der linken und rechten Elektroden, wie im unteren Einschub dargestellt. Bei negativer Vorspannung hat die linke Mn-APNR-Elektrode eine Fermi-Energie von μ _L = e |V _b |/2 und das rechte Cr-APNR μ _R =  − e |V _b |/2. Innerhalb des Transportfensters des Energiebereichs [μ _L ,μ _R ], gibt es nur einen sehr kleinen Teil des Spin-Down-Energiebandes in der Cr-APNR-Elektrode, so dass der Spin-Down-Strom niedrig bleibt. Im Gegensatz dazu existiert sowohl bei Mn- als auch bei Cr-APNR-Elektroden eine breite Überlappung der Spin-up-Energiebänder und der Spin-up-Strom steigt schnell mit der Vorspannung an. Im Transportfenster [μ _R ,μ _L ] bei positiver Vorspannung gibt es jedoch kein Spin-up-Energieband in der linken Elektrode und der entsprechende Strom bleibt fast Null, da Mn-APNR ein p . ist -Typ Halbleiter mit großer Bandlücke für Aufwärtsspin. Der Spin-Down-Strom beginnt bei V . zu steigen _b =0,2 V, wenn die rechte Fermi-Energie mit dem linken Spin-Down-Leitungsband ausgerichtet ist. In Abb. 7b tragen wir das Gleichrichtungsverhältnis α _σ = [Ich _σ (−|V _b |) − ich _σ (|V _b |)]/Ich _σ (|V _b |) des Spins σ als Funktion der Bias-Größe |V _b |. Um |V _b | = 0,5 V, der APNR-Spin p-n Junction hat eine Gleichrichtung von 2400 für Aufwärtsspin und nur 2 für Abwärtsspin.

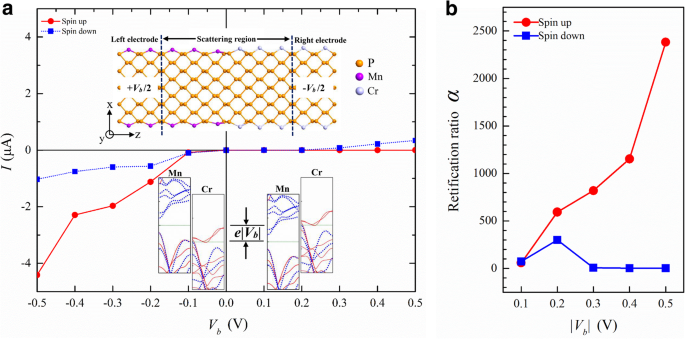
a Das spinabhängige I-V charakteristisch für einen Mn/Cr-9-APNR-Heteroübergang. Die Geometrie des Zwei-Sonden-Systems ist im oberen Einschub dargestellt. Die unteren Einschübe zeigen die Ausrichtungen der Elektrodenenergiebänder für negative und positive Vorspannungen. b Das entsprechende Gleichrichtungsverhältnis α wird gegen die Bias-Größe aufgetragen

Schlussfolgerungen

Die DFT-NEGF-Simulation legt nahe, dass die Kantenfunktionalisierung von TM-Atomen die elektrischen und magnetischen Eigenschaften von nichtmagnetischen Halbleiter-APNRs stark manipulieren und sie metallisch oder halbhalbleiterig machen kann. Die TM-Atome in TM-APNRs behalten ihre elektronischen Konfigurationen im isolierten Zustand, wobei der Magnetismus der V- und Mn-Atome hauptsächlich von d . stammt Orbitale, aber das von Cr von beiden d und s Orbitale. In Mn-APNRs ist das d Orbitale sind halb gefüllt. Das ganze Spin-up d Orbitale der Mn-Atome sind besetzt und der Spin-down d Orbitale liegen über dem Fermi-Niveau. Aufgrund der schmalen Bandlücke des d Orbital werden Mn-APNRs zu Halbhalbleitern, bei denen die Spin-down-Energiebänder eine viel engere Lücke auf dem Fermi-Niveau aufweisen als die Spin-up-Banden. Diese besondere Eigenschaft könnte für das Design von Spintronikvorrichtungen verwendet werden, da die Materialien unter geeigneten Bedingungen Halbleiter für einen Spin und Isolatoren für den anderen sein können. Mit Hilfe des Stark-Effekts auf Kantenzustände können die Energielücken durch ein angelegtes transversales elektrisches Feld weiter moduliert werden. Beispielsweise kann ein Feld von 5 V/nm die Bandlücke von Spin-Down-Elektronen schließen, während eine Lücke von 0,75 eV für Spin-Up-Elektronen aufrechterhalten wird. Unter Ausnutzung des drastischen Unterschieds im Energieband zwischen Mn- und Cr-APNRs können wir Spin p-n . entwerfen Dioden mit Mn/Cr-APNR-Übergang, bei denen eine starke Gleichrichtung nur für einen Spin auftritt.

Abkürzungen

1D:

Eindimensional

2D:

Zweidimensional

AFM:

Antiferromagnetisch

APNR:

Sessel schwarzes Phosphoren Nanoband

ATK:

Atomistix-Toolkits

DFT:

Dichtefunktionaltheorie

DOS:

Dichte der Zustände

FM:

Ferromagnetisch

NEGF:

Nicht-Gleichgewichts-Green-Funktion

TM:

Transition metal