Design eines abstimmbaren Ultra-Breitband-Terahertz-Absorbers basierend auf mehreren Schichten von Graphen-Bändern

Hintergrund

In den letzten Jahren hat sich das Terahertz-Band aufgrund der großen Anwendung in Spektroskopie, medizinischer Bildgebung, Modulatoren, Sicherheit und Kommunikation zu einer der interessantesten Plattformen entwickelt [1,2,3]. Der Terahertz-Absorber ist ein wichtiger Zweig, der in den oben genannten Bereichen praktische Anwendung finden kann [4,5,6]. Die schmale Bandbreite, der geringe Absorptionswirkungsgrad und die nicht einstellbare Absorptionsleistung der Absorber schränken ihre Anwendungsmöglichkeiten in der Praxis jedoch stark ein. Um die Anwendung von Terahertz-Absorbern besser auszuweiten, werden dringend weitere neue Geräte und Materialien benötigt. Graphen als zweidimensionales Material mit Wabengitterstruktur hat sich aufgrund seiner durch elektrisches Feld, Magnetfeld, Gatespannung und chemischer Dotierung gesteuerten Leitfähigkeit zu einem der vielversprechendsten Materialien entwickelt [7,8,9,10 ,11,12,13,14]. Graphen kann insbesondere Oberflächenplasmonen im Terahertz-Bereich unterstützen. Verglichen mit dem traditionellen Oberflächenplasmonenmaterial haben Graphen-Oberflächenplasmonen den Vorteil geringer Verluste, flexibler Abstimmbarkeit usw. [15,16,17,18,19].

Aufgrund der Überlegenheit von Graphenmaterialien in Terahertz-Absorbern wurden einige Graphen-Absorber vorgeschlagen und nachgewiesen [20,21,22,23,24,25,26,27,28,29,30,31,32,33 ,34]. Die theoretische Analyse bestätigt, dass eine einzelne Graphenschicht optisch transparent ist und eine Absorption von 2,3% hat [35,36,37]. Um die Begrenzung der elektromagnetischen Energie zu verbessern, wurden periodisch gemusterte Graphenstrukturen entworfen, wie zum Beispiel netzförmige [20,21,22], Anti-Punkte [23] und kreuzförmige [32]. Diese Absorber sind jedoch stark von komplex strukturiertem Graphen abhängig, was zu Herstellungsschwierigkeiten führt. Darüber hinaus ist das für den Betrieb verfügbare Band sehr schmal, und die meisten der berichteten Arbeiten haben keine Bandbreite von mehr als 1,5 Thz [20,21,22,23,24,25,26,27,28]. Um die Bandbreite zu verbreitern, wurden mehrere mehrschichtige Graphenstrukturen vorgeschlagen. Allerdings hängen die berichteten Mehrschichtstrukturen auch von einer sehr komplexen Struktur des Graphens ab und die Betriebsbandbreiten sind nicht lang genug [32,33,34]. Darüber hinaus haben Zhao et al. einen schaltbaren Terahertz-Absorber für die Anwendung als Amplitudenmodulator entwickelt [25]. Durch Steuerung des chemischen Potentials von Graphen von 0 bis 0,3 eV kann der Zustand der entworfenen Struktur von Absorption (> 90%) auf Reflexion (> 82%) im Frequenzbereich von 0,53–1,05 Thz umgeschaltet werden. Aber die Schaltintensität ist nicht hoch genug und die Modulationsbandbreite ist sehr schmal, was die weitere Anwendung in der Praxis einschränkt.

In diesem Artikel stellen wir einen abstimmbaren Terahertz-Absorber auf Graphenbasis aus mehrschichtigem Graphen vor, der eine ultrabreitbandige Absorption von über 90% im Frequenzbereich von 3–7,8 Thz erreichen kann. Das durchschnittliche Absorptionsvermögen des Absorbers beträgt mehr als 96,7%. Außerdem hat der vorgeschlagene Absorber eine höhere Schaltintensität, die Absorptionsamplitude kann von nahezu perfekter Absorption (> 90%) bis zu hoher Reflexion (> 90%) durch Änderung der Fermi-Energie der Graphenschicht in der gesamten Bandbreite von 4,8 Thz eingestellt werden. Wenn die Fermi-Energie von Graphen 0 eV beträgt, wird die vorgeschlagene Struktur ein nahezu perfekter Reflektor mit einer Reflexion von mehr als 97% im Hochfrequenzband (etwa 5,5 Thz später) sein. Darüber hinaus ist der Absorber unabhängig von den Einfallswinkeln mit einer Absorption von mehr als 90% bis 50°. Nach unserem besten Wissen schlagen wir zunächst die zweidimensionale mehrschichtige Graphen/Dielektrikum-Struktur vor, um eine ultrabreitbandige Absorption zu realisieren. Der vorgeschlagene Absorber ist einfach und hängt nicht von komplex strukturiertem Graphen ab, und das Design bietet großen Komfort für die Herstellung von mehrschichtigen Graphenstrukturen [38, 39]. Wichtig ist, dass das Design skalierbar ist, um breitere abstimmbare Terahertz-Absorber durch Hinzufügen weiterer Graphenschichten zu entwickeln, die in optoelektronischen Terahertz-Bauelementen breite Anwendung finden können.

Methoden

Das Diagramm der vorgeschlagenen Struktur ist in Abb. 1 gezeigt, die aus mehrschichtigem Graphen besteht, das in das Dielektrikum auf dem SiO₂ . eingebettet ist Schicht und einer dicken metallischen reflektierenden Platte auf der Unterseite. Wie in Abb. 1 gezeigt, ist oben Graphen mit unterschiedlicher Breite (W ) ist in einem bestimmten Abstand t . in das Dielektrikum eingebettet ₂ (t ₂ = 2 μm). Die Breite W jedes Graphens beträgt 5, 5, 27, 4, 4, 2, 21, 21 bzw. 26 µm (von oben nach unten). Jede Schicht ist symmetrisch um die z -Achse. Die Entfernung t ₁ zwischen der Unterseite der Graphenschicht und dem SiO₂ Schicht ist 2 µm. Die Dicke des Dielektrikums beträgt H ₁ . Die mittlere Schicht ist SiO₂ mit einer Dicke von H ₂ . Der Boden ist ein Metallfilm mit einer Dicke von D . Die Dauer der Einheit beträgt P. Diese Anfangswerte der Strukturparameter werden auf H . gesetzt ₁ = 21 μm, H ₂ = 7 μm, D = 0,5 μm, P = 32 μm. Das untere metallische Material ist Gold, und seine Permittivität kann wie folgt durch das Drude-Modell im Terahertz-Bereich richtig dargestellt werden:

wobei der Wert der konstanten Permittivität ε _∞ , Plasmafrequenz ω _p , und Kollisionshäufigkeit γ sind auf 1, 1,38 × 10 ¹⁶ . eingestellt rad/s und 1,23 × 10 ¹³ s ^− 1 , bzw. Die Permittivität des dielektrischen Materials und SiO₂ Material werden auf 3 bzw. 4 gesetzt.

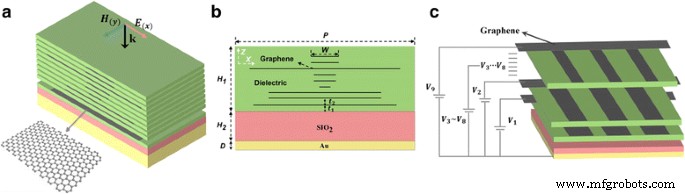
a Schematische Darstellung des Breitbandabsorbers auf Graphenbasis. b Querschnitt des Absorbers mit den zur Berechnung verwendeten Parametern. c Das Schema der externen Vorspannungsschaltung. Die Zweige der Spannung (V ₁ ~V ₉ ) sind jeweils mit verschiedenen Graphenschichten verbunden

In der Simulation wird Graphen als ultradünner Film behandelt, der in das Dielektrikum eingebettet ist. Die komplexe Oberflächenleitfähigkeit von Graphen, die von Interband- und Intraband-Beiträgen dominiert wird, kann mit der Kubo-Formel berechnet werden [40]:

wobei \({f}_d\left(\varepsilon\right)={\left({e}^{\left(\varepsilon -{E}_f\right)/{k}_BT}+1\right)} ^{-1} \) ist die Fermi-Dirac-Verteilung, w ist die Bogenfrequenz, ε ist die Energie, k _B ist die Boltzmann-Konstante, τ ist die Trägerrelaxationszeit, T ist die Temperatur (T = 300 K in unserer Arbeit), ℏ ist die reduzierte Plank-Konstante und E _f ist Fermi-Energie. Die Kubo-Formel (2) zeigt, dass die Oberflächenleitfähigkeit des komplexen Graphens durch die Fermi-Energie E . eingestellt werden kann _f . Die Graphen-Fermi-Energie jeder Schicht kann individuell durch die Vorspannung gesteuert werden, die Beziehung zwischen E _f und Vorspannung kann geschrieben werden als [41, 42]:

wo v _F = 0,9 × 10 ⁶ m/s ist die Femi-Geschwindigkeit, V ₀ ist der Spannungsoffset [41], \( {a}_0=\frac{\varepsilon_0{\varepsilon}_d}{ed} \), a ₀ ist das kapazitive Modell der Struktur, wobei ε ₀ ist die Permittivität im Vakuum. ε _d ist die Permittivität des Dielektrikums, d ist die Höhe des Dielektrikums und e ist die Ladung eines Elektrons. V _n (V ₁ ~V ₉ ), d. h. die an das Graphen angelegte Spannung kann aus der zusätzlichen Schaltung von Fig. 1c erhalten werden. Nach Formel (2) und (3) kann die Oberflächenleitfähigkeit von Graphen durch die angelegte Spannung gesteuert werden. Basierend auf dem Ampere-Gesetz im stationären Bereich und dem Ohmschen Gesetz kann die Permittivität von Graphen dann wie folgt erhalten werden:[43]:

In dem t _g ist die Dicke des Graphens, ε ₀ die Permittivität des Vakuums ist und σ _g ist die Oberflächenleitfähigkeit des Graphens. Gemäß Formel (4) kann die Permittivität von Graphen durch die Oberflächenleitfähigkeit ermittelt werden, die auch durch die angelegte Spannung ermittelt werden kann. Daher zeigen Formel (2–4), dass die elektromagnetischen Eigenschaften von Graphen dynamisch durch die angelegte Spannung gesteuert werden können, was dazu führt, dass auch die Absorptionseigenschaften der Struktur dynamisch gesteuert werden können.

Um das Absorptionsverhalten der entworfenen Struktur zu untersuchen, implementieren wir die numerischen Simulationen mit zweidimensionaler FDTD. In unserer Simulation setzen wir die Struktur auf eine periodische Randbedingung in x-Richtung. Ein Strahl einer ebenen Terahertzwelle fällt auf das Modell normalerweise entlang der z . ein Richtung mit seinem elektrischen Feld E entlang x Richtung. Die Bloch-Randbedingung wird auf den schiefen Einfall im periodischen Gefüge angewendet. Wir verwenden 1-R-T, um die Absorption des Modells zu berechnen, wobei R und T Reflektivität bzw. Transmission darstellen. Da die Dicke des Metalls viel größer ist als die Skin-Tiefe des einfallenden Lichts in das Metall, ist die Durchlässigkeit T null. Daher vereinfachen wir die Berechnungsformel für 1-R.

Ergebnisse und Diskussion

Zuerst stimmen wir die Spannung jeder Graphenschicht ab, um eine perfekte Absorption zu erreichen (von oben nach unten passen wir die Fermi-Energie E _f jeder Graphenschicht auf 0,9, 0,9, 1,1, 0,8, 0,8, 1,1, 1,1, 0,9 und 0,8 eV). Wie in Abb. 2 gezeigt, weist die vorgeschlagene Struktur von 3 bis 7,8 Thz eine Breitbandabsorption von über 90% innerhalb einer Bandbreite von 4,8 Thz auf. Die FWHM des Absorbers beträgt 5,4 Thz. Die Bandbreite beträgt etwa \( \frac{BW}{f_0}\times 100\% \) = 88,8% der Mittenfrequenz (hier BW ist die Bandbreite und f ₀ ist die Zentralfrequenz). Wir berechnen auch den durchschnittlichen Absorptionsgrad des Absorbers, der bis zu 96,7% beträgt. Andererseits mit dem E _f = 0 eV, die vorgeschlagene Struktur ist ein nahezu idealer Reflektor mit einer Reflexion von mehr als 90% über die gesamte Betriebsbandbreite und im Hochfrequenzband (etwa 5,5 Thz später) die Reflexion sogar von mehr als 97%. Natürlich können wir auch die Spannung jeder Graphenschicht abstimmen, um die gewünschte Amplitude zu erhalten, die in einigen Bereichen potenzielle Anwendungen haben kann.

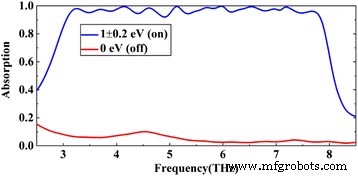
Die berechneten Absorptionsspektren des vorgeschlagenen Absorbers, wobei die blaue Linie die Absorption bei hoher Spannung und die rote Linie die Absorption ohne angelegte Spannung darstellt

Um die nahezu perfekte Absorption in einer ultrabreiten Bandbreite zu erklären, diskutieren wir zunächst die Situation einer einzelnen Graphenschicht. Wie in Abb. 3a gezeigt, entwerfen wir die Struktur mit nur einer einzigen Graphenschicht, die in das Dielektrikum eingebettet ist. Basierend auf Graphen-Oberflächenplasmonen untersuchen wir den Einfluss von Graphen-bezogenen Parametern auf die Absorptionsleistung von Absorbern, einschließlich der Fermi-Energie E _f , die Breite W , und die Position t von Graphen.

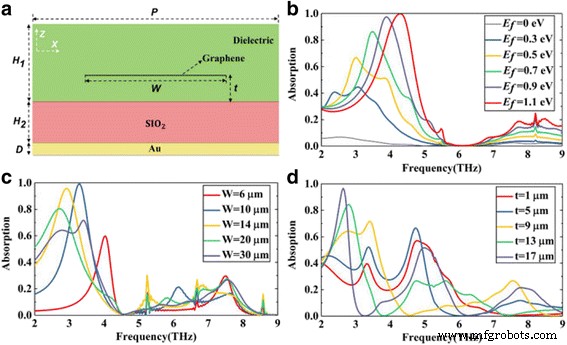
a Schematische Darstellung einer einschichtigen Graphenstruktur. b –d Die Absorption der Strukturbreite unterschiedlicher Fermi-Energie E _f , Breite W , und Position t des Graphenblattes bzw.

Abbildung 3b zeigt den Einfluss der Graphen-Fermi-Energie E _f im Absorptionsspektrum mit festem W und t . Als die Zunahme von E _f , wird die Oberflächenplasmonenresonanz des Graphens stärker, die Absorption der Struktur ist entsprechend höher. Der Absorptionspeak beträgt sogar mehr als 99% bei 4,3 Thz mit dem E _f = 1,1 eV. Und der Resonanzabsorptionspeak verschiebt sich zu einer höheren Frequenz, einer Blauverschiebung. In ähnlicher Weise zeigt Abb. 3c, d das Absorptionsspektrum der Struktur mit unterschiedlichen W oder t mit unverändertem E _f . Durch Variieren des W oder t der Graphenschicht werden die Amplitude und die Frequenz des Resonanzpeaks entsprechend geändert. Dieses Phänomen kann durch die Schaltungstheorie erklärt werden [28]. In dieser Theorie wird Graphen als Shunt-Admittanz beschrieben, dann kann das Ersatzschaltbild der Struktur mit Übertragungsleitungen und Graphen-Admittanz modelliert werden. Nach früheren Arbeiten [28] kann die Graphenadmittanz um die Breite W . geändert werden und die Fermi-Energie E _f des Graphens. Außerdem hängt die Admittanz der dem Dielektrikum entsprechenden Übertragungsleitungen von der Dicke des Dielektrikums ab. In unserer Struktur ist das Dielektrikum durch eine Graphenschicht getrennt. Somit ist die Position t der Graphenschicht beeinflusst auch die Eingangsadmittanz der Struktur.

Wie oben diskutiert, werden aufgrund des Einflusses von Graphen-bezogenen Parametern auf die Eingangsadmittanz der Struktur auch die Resonanzabsorptionspeaks des Modells beeinflusst. Wenn die Eingangsadmittanz der Struktur mit der Freiraumadmittanz übereinstimmt, wird die nahezu perfekte Absorption bei einer bestimmten Frequenz erreicht.

Um eine Breitbandabsorption zu erreichen, müssen wir dann die Resonanzabsorptionspeaks, die die Admittanzanpassung nahe beieinander erreichen, zulassen. Da die Absorptionspeaks nahe genug liegen, um zu verschmelzen, wird eine Breitbandabsorption erhalten. Daher fügen wir Graphenschichten hinzu, um mehr Resonanzabsorptionspeaks zu erhalten. Gleichzeitig passen wir die Parameter an, die die Resonanzspitze beeinflussen, einschließlich E _f , W , und t Admittanzabgleich zu implementieren. Zuerst fügen wir zwei Graphenschichten hinzu. Wie in Abb. 4a gezeigt, drei Schichten von Graphen mit unterschiedlicher Breite W sind in das Dielektrikum eingebettet. Es gibt ein bestimmtes Intervall t zwischen verschiedenen Graphenschichten oder dem unteren Graphen vom Dielektrikum. Wir passen die Graphen-bezogenen Parameter auf die entsprechenden Werte an, wobei wir t . festlegen = 2 μm, E _f = 0,9 eV und W = 26, 21 bzw. 20 µm (von unten nach oben).

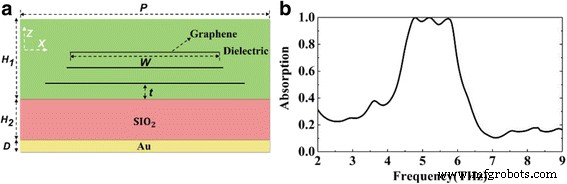
a Schematische Darstellung einer dreischichtigen Graphenstruktur. b Die berechneten Absorptionsspektren der dreischichtigen Graphenstruktur

Wie in 4b gezeigt, hat die Struktur eine nahezu perfekte Absorptionsbandbreite von 1,3 Thz mit einer Mittenfrequenz von 5,25 Thz. Drei Resonanzpeaks bei 4,7, 5,2 und 5,7 Thz werden entsprechend der Absorptionsamplitude von 99,9, 99,9 bzw. 99,1 % erhalten. Um eine ultrabreitbandige Absorption zu erreichen, ähnlich der dreischichtigen Graphenstruktur, fügen wir weitere Graphenschichten hinzu und passen die Graphenparameter jeder Graphenschicht auf die entsprechenden Werte an. Wir gehen davon aus, dass die strukturellen Parameter feststehen und die Produktion abgeschlossen ist; Wir können die Fermi-Energie von Graphen dynamisch anpassen, um eine Breitbandabsorption zu erreichen. Basierend auf dem Prinzip der Impedanzanpassung und den Forschungserfahrungen der dreischichtigen Graphenstruktur gehen wir zunächst davon aus, dass das Fermi-Niveau jeder Graphenschicht 1 eV beträgt. Wie in Abb. 5 (a) gezeigt, beträgt die Absorption der meisten Banden über 90% mit Ausnahme der Bande „1“ und „2“. Abbildung 5 (a–e) zeigt den schrittweisen Anpassungsprozess zur perfekten Absorption der „1“- und „2“-Bande. Nach Abb. 6e, f wird die Absorption der letzten Bande „1“ von der vierten Schicht (von unten nach oben) dominiert, daher passen wir die Fermi-Energie dieser Schicht individuell an. Wie in Fig. 7 gezeigt, ist die Absorptionsleistung am besten, wenn die Fermi-Energie 0,8 eV beträgt. Dies liegt daran, dass die Fermi-Energie die Impedanz von Graphen beeinflusst und dann die Eingangsimpedanz der gesamten Struktur beeinflusst. Die größere oder kleinere Fermi-Energie von Graphen führt zu einer Impedanzfehlanpassung. Von a nach b haben wir die Absorptionsleistung der „1“-Bande verbessert (im Band vor „1“ überlappen sich die Kurven a und b ungefähr). Ebenso finden wir, dass sich die Energieverteilung im „2“-Band hauptsächlich auf die 5., 8. und 9. Schicht konzentriert. Wir setzen zunächst die Fermi-Energie der 8. und 9. Graphenschicht auf 0,9 bzw. 0,8 eV. Wie in Abb. 5 gezeigt, beträgt die Absorption der verbleibenden Bande in „2“ von b bis c zusätzlich zu Dip „3“ und „4“ über 90%. Dann wird gemäß Abb. 6c Dip „3“ hauptsächlich durch die 5. Graphenschicht beeinflusst, wir setzen die Fermi-Energie auf 0,8 eV. Von c bis d wurde auch die Absorptionsleistung bei Dip „3“ verbessert. Gemäß Abb. 6d wird Dip „4“ jedoch von allen Graphenschichten beeinflusst. Daher passen wir die Fermi-Energie der verbleibenden Graphenschicht auf den entsprechenden Wert an. Von d bis e wird die nahezu perfekte Breitbandabsorption erreicht. Im Vergleich zu der in Abb. 4 gezeigten dreischichtigen Graphenstruktur werden mehr Resonanzabsorptionspeaks erhalten, Absorptionspeaks verschiedener Frequenzen liegen dicht beieinander und überlagern sich zu einer ultrabreitbandigen Absorption von über 90% mit einer Bandbreite von 4,8 Thz.

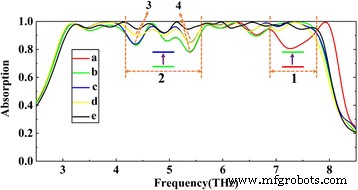
(a)–(e) zeigen den schrittweisen Anpassungsprozess für eine perfekte Absorption. Die Fermi-Energien jeder Graphenschicht (von unten nach oben) werden als (a) [1] eV, (b) [1, 1, 1, 0.8, 1, 1, 1, 1, 1] eV, (c ) [1, 1, 1, 0.8, 1, 1, 1, 0.9, 0.8] eV, (d) [1, 1, 1, 0.8, 0.8, 1, 1, 0.9, 0.8] eV und (e) [0.9, 0.9, 1.1, 0.8, 0.8, 1.1, 1.1, 0.9, 0.8] eV

a –f Die Verteilungen der elektrischen Feldamplitude (|E |) des vorgeschlagenen Absorbers bei verschiedenen Frequenzen

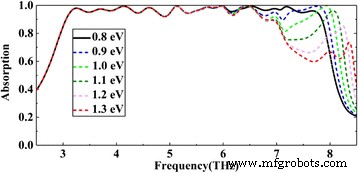
Absorptionsspektren mit unterschiedlichem E _f der vierten Graphenschicht und mit unverändertem E _f anderer Graphenschichten

Um den physikalischen Mechanismus hinter der ultrabreitbandigen nahezu perfekten Absorption zu verstehen, geben wir auch eine detaillierte Berechnung und Analyse der Verteilung der elektrischen Feldamplitude (|E|) der vorgeschlagenen Struktur bei verschiedenen Betriebsfrequenzen. Wie in Abb. 6 gezeigt, wird die Energie des Lichtfeldes zwischen den verschiedenen Schichten von Graphen und Dielektrikum begrenzt, was zu einer starken Absorption führt. Die Eigenschaften der elektrischen Feldverteilungen stimmen mit dem in Abb. 2 gezeigten Absorptionsspektrum überein. Bei einer bestimmten Frequenz beispielsweise zeigt Abb. 6b, dass die Begrenzung des elektrischen Felds hauptsächlich auf die starke Kopplung von Graphen und Dielektrikum aufgrund der Anregung zurückzuführen ist des lokalisierten Oberflächenplasmons (LSP) zeigt Fig. 6d, dass Graphen-Oberflächenplasmen eine wichtige Rolle bei der Eingrenzung des elektrischen Felds spielen. Die Anregung von lokalisiertem Oberflächenplasmon (LSP) und Graphenoberflächenplasmen tragen zusammen zur starken Absorption bei. Fig. 6a, b, d und Fig. 6c, e, f zeigen, dass die starke Kopplung zwischen Graphen und Dielektrikum bei einer bestimmten Frequenz durch Mehrschicht-Graphen bzw. Monoschicht-Graphen verursacht werden kann. Die Stapelung hoher Absorption bei verschiedenen Frequenzen erzeugt eine Breitbandabsorption unter der Einwirkung aller Graphenschichten.

Um beispielsweise den Stapeleffekt besser zu veranschaulichen, wird nach Abb. 6e, f die Absorption der letzten Bande (ca. 6,5 Thz später) hauptsächlich von der vierten Graphenschicht (von unten nach oben) dominiert. Also stimmen wir die Spannung dieser Graphenschicht ab. Wie in Fig. 7 gezeigt, nimmt mit der Zunahme der Fermi-Energie der vierten Graphenschicht die Absorptionsamplitude der Bande nach etwa 6,5 ​​Thz allmählich zu, aber es gibt fast keine Änderung in der Bande vor 6,5 Thz. In ähnlicher Weise können wir auch unabhängig ein bestimmtes Band einstellen, das hauptsächlich von anderen Graphenschichten beeinflusst wird. Alle Banden, die unabhängig voneinander auf hohe Absorption eingestellt werden können, werden überlagert, um schließlich eine breitbandige Absorption zu bilden. Wie bei der Analyse von Abb. 7 zeigt das Phänomen der unabhängigen Anpassung weiter, dass der Stapeleffekt aller Graphenschichten eine nahezu perfekte Breitbandabsorption erreicht.

Wie oben diskutiert, spielt die starke Kopplung zwischen Graphen und dem Dielektrikum eine wichtige Rolle bei der Breitbandabsorption. In den praktischen Anwendungen hoffen wir, dass die Breitbandabsorption unempfindlich gegenüber den Einfallswinkeln ist. Wie in Abb. 8 gezeigt, untersuchen wir den Einfluss der Einfallswinkel auf den Absorber. Aus Abb. 8 können wir entnehmen, dass der vorgeschlagene Absorber gegenüber Einfallswinkeln unempfindlich ist. Obwohl sich der Einfallswinkel auf 30° geändert hat, ist die Absorptionsleistung der Struktur nahezu unverändert. Wenn der Einfallswinkel auf 50° ansteigt, behält der Absorber trotz verringerter Absorptionseffizienz immer noch eine hohe Absorption von mehr als 90% über die gesamte Betriebsbandbreite bei. Daher kann der Absorber mit hoher Absorptionseffizienz über einen großen Einfallswinkelbereich gut arbeiten.

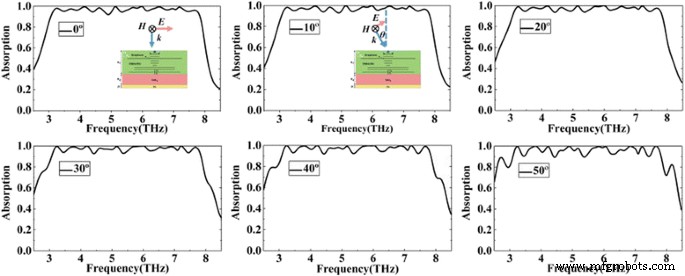
Die berechneten Absorptionsspektren des Absorbers mit unterschiedlichen Einfallswinkeln

Unter Berücksichtigung der Schwierigkeiten der Mehrschichtstruktur bei der Herstellung diskutieren wir schließlich den Einfluss der relevanten Strukturparameter auf die Absorberleistung. Abbildung 9a, b zeigen die Absorptionsspektren des vorgeschlagenen Absorbers mit unterschiedlicher Dicke der dielektrischen Schicht H ₁ und mit unterschiedlicher Dicke des SiO₂ Schicht H ₂ , bzw. Wie in Abb. 9a gezeigt, ist die am besten geeignete Höhe des Dielektrikums H ₁ beträgt 21 µm. Auf dieser Grundlage H ₁ 0,5 µm erhöhen oder verringern, die Leistung des Absorbers ändert sich fast nicht. Auch wenn H ₁ sich um 1 µm ändert, behält der Absorber in den meisten Bändern mit Ausnahme des Bandes um 7 Thz immer noch eine Absorption von über 90 % bei. Wie in Abb. 9b gezeigt, verglichen mit H ₁ , der Absorber reagiert empfindlicher auf die Höhe des SiO₂ H ₂ . Auch in diesem Fall behält der Absorber neben dem Band um 6 und 7,1 Thz auch in den meisten Bändern eine gute Leistung. Wie oben besprochen, können wir feststellen, dass, obwohl die Dicke der dielektrischen Schicht und des SiO₂ Schicht sogar im Mikrometerbereich verändert werden, behält der Absorber bei den meisten Wellenlängen immer noch eine gute Absorptionsleistung bei, was die Robustheit des Absorbers bei der Herstellung erheblich verbessert.

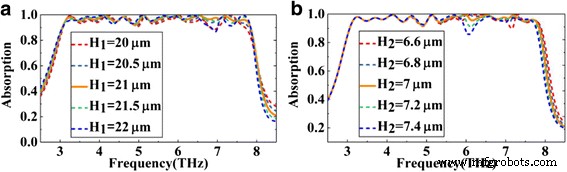
Die simulierten Absorptionsspektren des vorgeschlagenen Absorbers mit unterschiedlicher Dicke der dielektrischen Schicht und mit unterschiedlicher Dicke des SiO₂ Schicht entsprechend a und b

Schlussfolgerungen

In diesem Artikel schlagen wir einen ultrabreitbandigen, abstimmbaren Terahertz-Absorber auf Graphenbasis vor, der aus mehreren Schichten aus Graphen/Dielektrikum besteht. Der vorgeschlagene Absorber kann durch Veränderung der Fermi-Energie E . eine Breitbandabsorption von über 90% mit einer Bandbreite von 4,8 Thz erreichen _f verschiedener Graphenschichten. Mit dem E _f = 0 eV, das vorgeschlagene Design wird ein nahezu idealer Reflektor mit einer Reflexion von mehr als 90% innerhalb der gesamten Betriebsbandbreite von 3–7,8 Thz sein. Die ultrabreitbandige Absorption wird dem Stapeleffekt einer starken Resonanzabsorption bei verschiedenen Frequenzen zugeschrieben, die durch lokalisierte Oberflächenplasmonen (LSP) und Graphenoberflächenplasmonen angeregt werden. Darüber hinaus ist der vorgeschlagene Absorber unempfindlich gegenüber den Einfallswinkeln, und wir stellen auch fest, dass die Dicke der dielektrischen Schicht und das SiO₂ Schicht wenig Einfluss auf die Absorptionsleistung hat, was für praktische Anwendungen vorteilhafter ist. Darüber hinaus ist der vorgeschlagene Absorber einfach, der nicht von komplex strukturiertem Graphen abhängt, und die Bandbreite kann durch Hinzufügen weiterer Graphenschichten erweitert werden. Dieser abstimmbare Breitbandabsorber kann große potenzielle Anwendungen in Fotodetektoren, Bildgebung und Modulatoren haben.

Abkürzungen

FDTD:

Zeitbereich mit endlicher Differenz

LSP:

Lokalisiertes Oberflächenplasmon