Dynamisch abstimmbare plasmoneninduzierte Transparenz in einem On-Chip-Graphen-basierten asymmetrischen Nanohohlraum-gekoppelten Wellenleitersystem

Hintergrund

Plasmoninduzierte Transparenz (PIT), ein neuartiges Phänomen, das analog zum elektromagnetisch induzierten Transparenzeffekt (EIT) ein scharfes Transparenzfenster innerhalb eines breiten Absorptionsspektrums erzeugt [1], hat aufgrund seiner potenziellen Anwendungen in einem weiten Bereich von große Aufmerksamkeit auf sich gezogen Felder wie langsames Licht [2, 3], optisches Schalten [4], Lichtspeicherung [5] und hochempfindliche Wahrnehmung [6, 7]. Die PIT-basierten Geräte können aufgrund der großen lokalen Feldverstärkungsfähigkeit und der Überwindung der klassischen Beugungsgrenze des Lichts, die durch die Oberflächenplasmonenpolaritonen (SPPs) bereitgestellt wird, mit ultrakompakter Grundfläche realisiert werden [8, 9]. Es wurde eine Vielzahl von Designs vorgeschlagen, um einen PIT-Effekt in plasmonischen Nanostrukturen zu erzielen, einschließlich gekoppelter Resonatorsysteme [10,11,12,13], photonischer Kristallstrukturen [14, 15] und Metamaterialstrukturen [16, 17]. Die meisten dieser Strukturen mit PIT-Effekt sind jedoch kaum abstimmbar, es sei denn, die geometrischen Parameter der Strukturen werden geändert, was die aktive Steuerung von PIT-Fenstern in hohem Maße einschränkt und die Qualität verschlechtert.

Graphen, eine Monoschicht aus Kohlenstoffatomen, die in einem zweidimensionalen (2D) Wabengitter angeordnet sind [18], zeigt aufgrund seiner außergewöhnlichen elektrischen und optischen Eigenschaften, einschließlich der Fähigkeit zu extremer Einschließung, großes Potenzial für die Entwicklung hocheffizienter optoelektronischer Bauelemente [19,20, 21], dynamische Abstimmbarkeit und relativ geringe Dämpfungsverluste [22, 23]. Insbesondere die Oberflächenleitfähigkeit von Graphen kann durch chemisches Potential über externe Gatespannung oder chemische Dotierung dynamisch eingestellt werden [24, 25], was Graphen zu einem vielversprechenden Kandidaten für die Entwicklung abstimmbarer PIT macht, während die geometrischen Parameter festgelegt sind. Aufgrund dieser außergewöhnlichen Eigenschaften im Vergleich zu denen herkömmlicher Edelmetalle wurde eine breite Palette von Forschungen durchgeführt, um graphenbasierte PIT zu realisieren, wie PIT-Phänomene in graphenringresonatorgekoppelten Graphenwellenleitern [26, 27] und PIT-Effekte in a Graphen-basierter Nanoband-Wellenleiter gekoppelt mit einer rechteckigen Resonatorstruktur aus Graphen [28, 29]. Sonneet al. untersuchten die periodisch gemusterte Graphen-Doppelschichtstruktur, die durch eine dielektrische Schicht im Terahertz-Frequenzbereich getrennt ist, wo die multispektralen PIT-Antworten erreicht wurden [30]. Darüber hinaus werden abstimmbare PIT-Effekte in den periodisch kombinierten Graphen-Nanostreifen realisiert und mit dem gekoppelten Lorentz-Oszillator-Modell analytisch beschrieben [31, 32]. Die meisten früheren Arbeiten befassten sich jedoch mit Graphen-Resonatoren, die an ein Monolayer-Graphen- oder ein Graphen-Nanoband-Wellenleitersystem gekoppelt sind, und Graphen-Nanostreifen-Systeme mit normal einfallendem Licht. Es gab nur sehr wenige oder sogar keine Studien über das plasmonisch induzierte Transparenzphänomen in einer Graphenschicht mit lokal unterschiedlichen chemischen Potentialen. Darüber hinaus hat die Ausbreitung in der Ebene im Vergleich zu normal einfallendem Licht überwältigende Vorteile für die On-Chip-Integration.

Motiviert durch die obigen grundlegenden Studien schlagen wir in diesem Artikel eine Graphen-basierte plasmonische Nanostruktur vor, die aus einem plasmonischen Buswellenleiter besteht, der seitlich an eine U-förmige Nanokavität und eine rechteckige Nanokavität auf derselben Graphen-Monoschicht gekoppelt ist. Die kommerzielle Software COMSOL Multiphysics basierend auf der Finite-Elemente-Methode (FEM) wird verwendet, um die Transmission und das elektromagnetische Verhalten unserer Designs zu untersuchen. Simulationsergebnisse zeigen, dass das PIT-Phänomen in unserer vorgeschlagenen plasmonischen Nanostruktur beobachtet wird. Außerdem kann das PIT-Fenster durch Variieren der chemischen Potentiale der Nanohohlräume und des plasmonischen Buswellenleiters effektiv abgestimmt werden. Außerdem wird eine Theorie des gekoppelten Modus (CMT) eingeführt, um die Übertragungsmerkmale des PIT-Phänomens zu erklären. Schließlich wird ein plasmonischer Brechungsindexsensor basierend auf der vorgeschlagenen plasmonischen Nanostruktur untersucht. Die Sensibilität von 333,3 nm/Brechungsindexeinheit (RIU) wird bei der PIT-Transmissionsspitze erreicht. Auch der Slow-Light-Effekt mit Gruppenverzögerung über 1 ps wird realisiert. Diese vorgeschlagene neuartige plasmonische Nanostruktur könnte eine neue Möglichkeit bieten, eine graphenbasierte On-Chip-Integration plasmonischer Bauelemente mit hoher Dichte auf einer Graphen-Monoschicht zu realisieren.

Methoden

Der Einfachheit halber wird die vorgeschlagene Struktur durch eine suspendierte Graphen-Monoschicht mit lokaler Variation des chemischen Potentials modelliert, um den entsprechenden Buswellenleiter und die Nanoresonatoren zu bilden. 1a zeigt die schematische Konfiguration und die geometrischen Parameter einer U-förmigen Nanokavität, die direkt an einen plasmonischen Buswellenleiter gekoppelt ist. Der U-förmige Nanokavitäten-gekoppelte Wellenleiter mit einem chemischen Potential von μ _c2 ist von derselben Graphenschicht mit einem chemischen Potential von μ . umgeben _c1 . Die Breite des plasmonischen Buswellenleiters d beträgt 20 nm. Die Breite und Höhe der U-förmigen Nanokavität beträgt W _U = 150 nm und L _U =120 nm bzw.. Eine exakte theoretische Modellierung einer solchen Struktur erfordert eine dreidimensionale (3D) Berechnung, die extrem zeit- und speicherintensiv ist. Um dieses Problem zu lösen, wurde in vielen Veröffentlichungen die Methode des effektiven Index verwendet [33,34,35], und der Brechungsindex der Struktur wird durch den effektiven Index der geführten Moden ersetzt, der durch das Verhältnis zwischen der Ausbreitungskonstanten und die Wellennummer im freien Raum. In unserer Struktur wird die Graphenschicht als ultradünner Film behandelt, der durch einen effektiven Index gekennzeichnet ist, der als n . definiert ist _eff = β /k ₀ , wobei k ₀ = 2π /λ ist die Wellenzahl im freien Raum. Die Ausbreitungskonstante β des von Monolayer-Graphen unterstützten geführten SPP-Modus wird geschrieben als [36, 37]

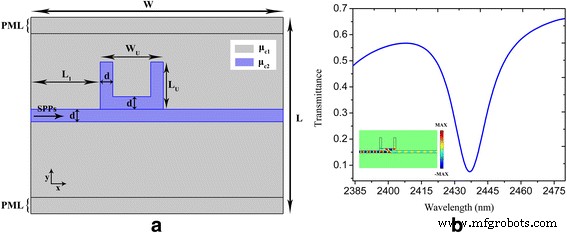
a, b Die schematische Konfiguration und die geometrischen Parameter eines U-förmigen Nanohohlraum-gekoppelten Wellenleitersystems bzw. die entsprechende spektrale Transmission. Der Einschub in b zeigt das elektrische Feld (E _y ) Verteilung bei einer Wellenlänge von 2437 nm. Die Parameter sind als W . eingestellt = 800 nm, L = 620 nm, d = 20 nm, W _U = 150 nm, L _U = 120 nm, L ₁ = 220 nm, τ = 1 ps, μ _c1 = 0,3 eV und μ _c2 = 0,9 eV. Die perfekt aufeinander abgestimmten Schichten (PML ) mit einer Breite von 50 nm sind auf der oben implementiert und unten des Berechnungsbereichs, um unerwünschte Reflexionen von der Bereichsgrenze zu eliminieren

wobei μ ₀ und ε ₀ die Permeabilität bzw. Permittivität des Vakuums darstellen und μ _r und ε _r repräsentieren die relative Permeabilität bzw. die relative Permittivität. Die Oberflächenleitfähigkeit von Graphen σ _g zusammengesetzt aus den Interband-Elektronenübergängen σ _inter und die Intraband-Elektronen-Photonen-Streuung σ _intra wird durch die Kubo-Formel gegeben [38, 39]

Mit

wobei μ _c ist das chemische Potenzial von Graphen, ω ist die Kreisfrequenz des Plasmons, ћ ist die reduzierte Planck-Konstante, e ist die Elektronenladung, k _B ist die Boltzmann-Konstante, T ist die Temperatur, ℏ = h/2π die reduzierte Planck-Konstante ist und τ ist die Elektronenimpulsrelaxationszeit. Konkret kann das chemische Potenzial von Graphen durch chemische Dotierung oder elektrisches Gating eingestellt werden [25, 26]. Michailowet al. haben experimentell gezeigt, dass die Ladungsträgerdichte in einer Graphenschicht bis zu 10 ¹⁴ . beträgt cm ⁻² erreicht, was zu einem chemischen Potential von 1–2 eV bei einer Temperatur unter 250 K führte [40]. Darüber hinaus wurde nachgewiesen, dass hochwertiges suspendiertes Graphen mit einer Gleichstrommobilität von bis zu 10 ⁵ cm ² V ⁻¹ s ⁻¹ erhalten werden, was τ . entspricht> 1,5 ps [41]. In diesem Papier sind sowohl die Relaxationszeit als auch das chemische Potenzial, die wir festlegen, konservativ genug, um die Zuverlässigkeit unserer numerischen Studie zu gewährleisten.

Ergebnisse und Diskussion

Wenn die SPP-Welle durch den in 1a gezeigten seitlich gekoppelten U-förmigen Nanohohlraum hindurchgeht, wird die Energie in den Nanohohlraum eingekoppelt. Bei der Resonanzwellenlänge wird aufgrund der destruktiven Interferenz zwischen der einfallenden Welle und der entweichenden Leistung aus der Nanokavität ein tiefes Transmissionstal erhalten [12, 13]. Abbildung 1b zeigt das Transmissionsspektrum einer U-förmigen Nanokavität, die direkt an einen plasmonischen Buswellenleiter mit τ . gekoppelt ist = 1 ps, μ _c1 = 0,3 eV und μ _c2 = 0,9 eV. Bei der Resonanzwellenlänge von 2437 nm wird ein ausgeprägter Einbruch mit einer Transmission von weniger als 0,1 erreicht. Der Einschub in Abb. 1b zeigt die entsprechende Verteilung des elektrischen Feldes bei der Resonanzwellenlänge, wobei zu sehen ist, dass sich fast keine SPPs durch den plasmonischen Wellenleiter ausbreiten. Abbildung 2a zeigt die Transmissionsspektren mit unterschiedlicher Relaxationszeit τ =0,6, 0,8 und 1 ps, wobei zu erkennen ist, dass mit zunehmender Relaxationszeit ein höherer Transmissionskontrast erreicht wird. Dies wird auf die Verringerung der ohmschen Absorption der Plasmonen mit zunehmender Relaxationszeit des Elektronenimpulses zurückgeführt [39]. Die berechnete Transmission eines U-förmigen Nanokavitäten-gekoppelten Wellenleitersystems für verschiedene chemische Potentiale μ _c2 ist in Abb. 2b dargestellt. Die Entspannungszeit τ und chemisches Potenzial μ _c1 werden konstant auf 1 ps bzw. 0,3 eV gehalten. Man kann sehen, dass die Orte der Einbrüche dynamisch über das unterschiedliche chemische Potenzial des Nanohohlraums und des Buswellenleiters abgestimmt werden. Die zentralen Wellenlängen der Dips sind 2455, 2445 und 2437 nm mit μ _c2 = 0,89, 0,895 bzw. 0,9 eV.

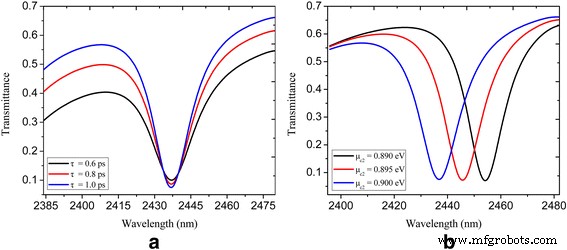
Spektraler Transmissionsgrad eines U-förmigen nanocavity-gekoppelten Wellenleitersystems in Abb. 1:a mit τ =0,6, 0,8 und 1 ps; μ _c1 = 0,3 eV; und μ _c2 = 0,9 eV; b mit μ _c2 = 0,89, 0,895 und 0,9 eV; μ _c1 = 0,3 eV; und τ = 1 ps

Nach CMT [12, 42, 43] ist die spektrale Transmission des Systems, das einen Resonanzmodus der Frequenz unterstützt, ω ₀ kann geschrieben werden als

wobei 1/τ _ich und 1/τ _e repräsentieren die Abklingrate des intrinsischen Verlustes in der Nanokavität bzw. der durch den plasmonischen Bus-Wellenleiter entweichenden Leistung. Offensichtlich ist die minimale Transmission T _min = (1/τ _ich ) ² /(1/τ _ich + 1/τ _e ) ² erreicht werden, wenn die Frequenz des einfallenden Lichts ω gleich der Resonanzfrequenz ω ₀ . Als 1/τ _e ist viel mehr als 1/τ _ich , kann ein Transmissionseinbruch von nahezu Null erreicht werden, was gut mit den Simulationsergebnissen übereinstimmt.

Um PIT-Effekte zu erzielen, fügen wir eine rechteckige Nanokavität basierend auf der in Abb. 1 gezeigten plasmonischen Nanostruktur hinzu. Eine Graphen-basierte plasmonische Nanostruktur bestehend aus einem plasmonischen Buswellenleiter, der seitlich an U-förmige und rechteckige Nanohohlräume gekoppelt ist, ist in Abb. 1 schematisch dargestellt 3a. Zwischen den beiden Nanohohlräumen besteht eine starke Kopplung, wenn sie über den plasmonischen Bus-Wellenleiter verbunden sind. Die destruktive Interferenz zwischen zwei resonanten Anregungspfaden in Bezug auf die U-förmigen und rechteckigen Nanokavitäten erzeugt das PIT-Phänomen [10, 11]. Wie in Fig. 3b gezeigt, erschien ein scharfer Transmissionspeak (erhöht von 0,06 auf 0,44) in dem in Fig. 1b gezeigten verbotenen Transmissionsband, was die Bildung des PIT-Fensters impliziert. Die zentrale Wellenlänge des PIT-Fensters beträgt 2437 nm, was genau der Ort der zentralen Wellenlänge des in 1b gezeigten Transmissionstiefs ist. Die breite Resonanz der U-förmigen Nanokavität wird in zwei Resonanzmoden aufgeteilt:eine ist blau- und die andere rotverschoben [12, 13]. Abbildung 3c–e zeigt die elektrischen Feldverteilungen der Resonanzmoden bei 2408, 2437 bzw. 2457 nm. Wir können sehen, dass die elektrische Feldverteilung in den Nanohohlräumen bei 2437 nm mit der elektrischen Feldverteilung in plasmonischen Buswellenleitern phasengleich ist, was bedeutet, dass das einfallende Licht und das aus den Nanohohlräumen in den plasmonischen Buswellenleiter austretende Licht eine kohärente Verstärkung erfahren . Darüber hinaus zeigen die elektrischen Feldverteilungen, dass zwischen den Nanokavitäten und dem plasmonischen Bus-Wellenleiter bei 2408 und 2457 nm eine Gegenphase besteht, dh die Bedingungen der destruktiven Resonanz sind erfüllt, was zur Hemmung der Übertragungswellen führt [12].

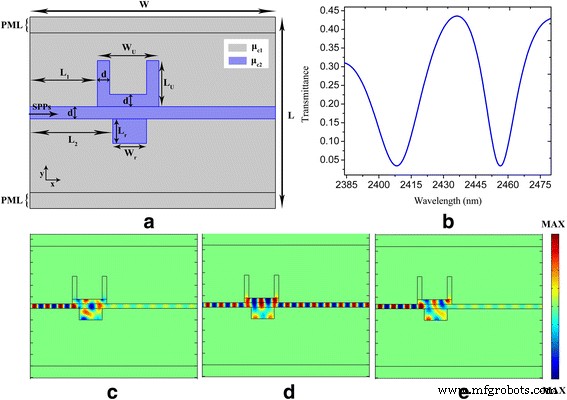
a, b Die schematische Konfiguration und die geometrischen Parameter des U-förmigen und rechteckigen nanocavity-gekoppelten Wellenleitersystems bzw. die entsprechende spektrale Transmission. c –e Elektrisches Feld (E _y ) Verteilung bei Wellenlängen von 2408, 2437 bzw. 2457 nm. Die Parameter sind als W . eingestellt = 800 nm, L = 620 nm, d = 20 nm, W _U = 150 nm, L _U = 120 nm, L ₁ = 220 nm, L ₂ = 250 nm, L _r = 50 nm, W _r = 100 nm, τ = 1 ps, μ _c1 = 0,3 eV und μ _c2 = 0,9 eV

Wir berechnen die spektrale Transmission für das U-förmige und rechteckige Nanocavity-gekoppelte plasmonische Bus-Wellenleitersystem mit variierter Relaxationszeit τ =0,6, 0,8 und 1 ps, und die Ergebnisse sind in Fig. 4a gezeigt. Man sieht, dass der Transmissionskontrast mit zunehmender Relaxationszeit zunimmt. Darüber hinaus ist die dynamische Durchstimmbarkeit des PIT-Fensters in 4b gezeigt. Das chemische Potenzial μ _c1 wird konstant auf 0,3 eV gehalten, während μ _c2 0,89, 0,895 und 0,9 eV beträgt. Als chemisches Potential μ _c2 erhöht, ist der Transmissionspeak (bei den Wellenlängen 2452, 2445 und 2437 nm) im PIT-Fenster offensichtlich blauverschoben. Als Ergebnis wird der dynamisch abstimmbare PIT-Effekt in unserer vorgeschlagenen Nanostruktur durch Modifizieren des chemischen Potenzials der Nanohohlräume und des plasmonischen Buswellenleiters realisiert.

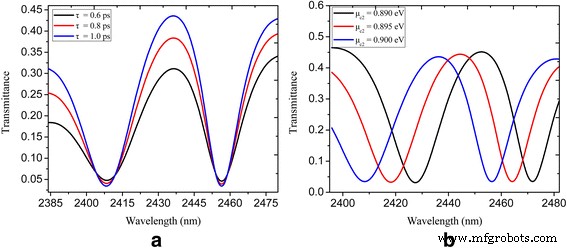
Die spektrale Transmission eines U-förmigen und rechteckigen nanocavity-gekoppelten Wellenleitersystems, gezeigt in Abb. 3:a mit τ =0,6, 0,8 und 1 ps; b mit μ _c2 = 0,89, 0,895 und 0,9 eV

Um zu untersuchen, wie die geometrischen Parameter das PIT-Phänomen beeinflussen, haben wir die Position der rechteckigen Nanokavität modifiziert. Abbildung 5a zeigt die spektrale Transmission des U-förmigen und rechteckigen nanocavity-gekoppelten plasmonischen Bus-Wellenleitersystems, wobei zu sehen ist, dass der Transmissionspeak höher wurde (von 0,44 auf 0,52 erhöht) und das PIT-Fenster breiter wird mit L ₂ für einen bestimmten Bereich ansteigend, was auf die Intensivierung der Kopplungsstärke zwischen den beiden Nanokavitäten zurückgeführt wird [11, 28]. Außerdem stellen wir fest, dass die Verringerung der Breite des rechteckigen Nanohohlraums zu einem höheren Transmissionspeak (erhöht von 0,44 auf 0,48) führen kann, wie in Fig. 5b gezeigt. Dies bietet eine weitere Möglichkeit, das PIT-Fenster abzustimmen. Der Qualitätsfaktor (Q-Faktor) der PIT-Fenster ist definiert als λ ₀ /∆λ , wobei λ ₀ und λ sind die Transmissionsspitzenwellenlänge und die Halbwertsbreite (FWHM). In unserer vorgeschlagenen plasmonischen Nanostruktur wird eine FWHM von weniger als 30 nm und ein Q-Faktor von etwa 80 erhalten, was viel schmaler und höher ist als die in den oben genannten Literaturstellen vorgeschlagenen Gegenstücke der graphenbasierten PIT [28, 29].

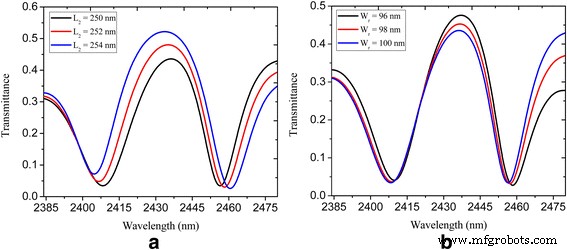
Spektrale Transmission eines U-förmigen und rechteckigen nanocavity-gekoppelten Wellenleitersystems, gezeigt in Abb. 3:a mit L ₂ =250, 252 und 254 nm; b mit W _r = 96, 98 und 100 nm

Gemäß CMT wird die Transmission in unserer plasmonischen Nanostruktur ausgedrückt als [12, 42]

wo γ und β stehen für den Kopplungskoeffizienten zwischen den beiden Nanokavitäten bzw. den Kopplungskoeffizienten zwischen den Nanokavitäten und dem plasmonischen Buswellenleiter. Wir können feststellen, dass das PIT-Fenster erhalten werden kann, wenn die Resonanzfrequenzen der U-förmigen Nanokavität ω _U und die rechteckige Nanokavität ω _r sind ungefähr gleichwertig. Und der entsprechende Transmissionspeak ist |( γ + 1)/(β + γ + 1)| ² .

Basierend auf der in Abb. 3a gezeigten Struktur konstruieren wir den Brechungsindexsensor, der durch Modifizieren der relativen Permittivität in Gl. 1. Abbildung 6a veranschaulicht die spektrale Durchlässigkeit mit unterschiedlichem Brechungsindex n , die sich auf den Brechungsindex des Undersensing-Materials bezieht. Man kann sehen, dass sich die Wellenlängen von Peak/Dip1/Dip2 von 2437,3 zu 2457,3 nm/2410,3 zu 2432,4 nm/2457.3 zu 2474,9 nm verschieben, wenn der Brechungsindex n variiert von 1 bis 1.06. Als Brechungsindex n zunimmt, zeigen sowohl die Transmissionsspitze als auch die Einbrüche eine Rotverschiebung. Die Erfassungsempfindlichkeit des Brechungsindexsensors, definiert als die Verschiebung der Peak/Dip1/Dip2-Wellenlänge pro Einheitsvariation des Brechungsindex dλ/dn beträgt 333,3, 368,3 bzw. 293,3 nm/RIU. Abbildung 6b zeigt die Peaks und Dips der spektralen Transmission mit Brechungsindex n variierend von 1 bis 1,19, wobei wir die ungefähr lineare Beziehung der Peak/Dip-Wellenlängen gegenüber dem Brechungsindex n . sehen können .

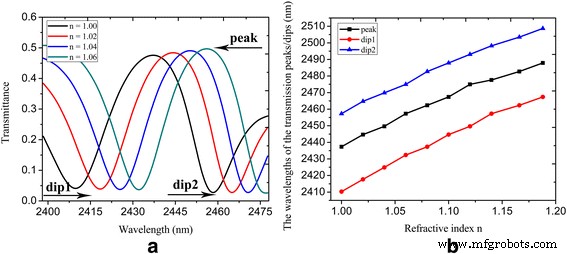
a Die spektrale Transmission mit Brechungsindex n =1, 1,02, 1,04 und 1,06; b die Peak-/Dip-Wellenlängen der spektralen Transmission gegenüber dem Brechungsindex n . Die Parameter sind als W . eingestellt = 800 nm, L = 620 nm, d = 20 nm, W _U = 150 nm, L _U = 120 nm, L ₁ = 220 nm, L ₂ = 250 nm, L _r = 50 nm, W _r = 96 nm, τ = 1 ps, μ _c1 = 0,3 eV und μ _c2 = 0,9 eV

Es ist bekannt, dass das PIT-Phänomen von einem langsamen Lichteffekt begleitet wird, der durch die scharfe Dispersion verursacht wird [13, 29]. Der Slow-Light-Effekt kann durch die Gruppenlaufzeit charakterisiert werden, die als τ . ausgedrückt wird _g = ∂φ (ω )/∂ ω wo φ (ω ) ist die effektive Phasenverschiebung des Transmissionsspektrums. In Abb. 7 tragen wir die Gruppenverzögerungen innerhalb des PIT-Fensters bei verschiedenen chemischen Potentialen μ _c2 . In der Nähe der PIT-Übertragungsspitze bietet es große positive Gruppenlaufzeiten, die den langsamen Lichteffekt anzeigen. Die Spitzenwellenlängen des PIT-Systems bei μ _c2 =0,89, 0,895 und 0,9 eV sind 2449,7, 2442,3 bzw. 2434,7 nm, und die entsprechenden Gruppenverzögerungen betragen 0,99, 1,1 bzw. 1,02 ps. Somit wird der Slow-Light-Effekt durch Modifizieren des chemischen Potentials der Nanohohlräume und des plasmonischen Buswellenleiters effektiv abgestimmt. Es sollte auch darauf hingewiesen werden, dass es sich um einen Proof-of-Concept-Artikel handelt. In Wirklichkeit sollte die vorgeschlagene Struktur auf dem Substrat liegen, wo der Brechungsindex größer ist als die von Luft, und der Frequenzgang würde sich entsprechend verschieben. Außerdem ist der Einschluss des Plasmons höher, begleitet von der Zunahme des Verlustes, was zu einer Verringerung des Spitzenwertes des Transparenzfensters im Transmissionsspektrum führt. Das Prinzip ist jedoch identisch mit dem suspendierten Fall.

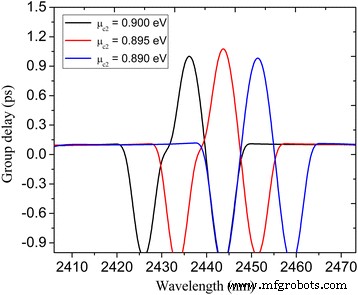
Die Gruppenverzögerungen gegenüber dem chemischen Potenzial μ _c2 für das in Abb. 3a gezeigte Graphen-PIT-System. Die anderen Parameter sind als W . eingestellt = 800 nm, L = 620 nm, d = 20 nm, W _U = 150 nm, L _U = 120 nm, L ₁ = 220 nm, L ₂ = 254 nm, L _r = 50 nm, W _r = 96 nm, τ = 1 ps, μ _c1 = 0,3 eV

Schlussfolgerungen

Zusammenfassend wurden dynamisch abstimmbare PIT-Effekte in Graphen-basierten plasmonischen Nanostrukturen, die aus einem plasmonischen Bus-Wellenleiter bestehen, der seitlich an U-förmige und rechteckige Nanohohlräume gekoppelt ist, vorgeschlagen und unter Verwendung der Finite-Elemente-Methode modelliert. Die dynamische Durchstimmbarkeit der PIT-Fenster wird durch Modifizieren des chemischen Potentials der Nanohohlräume und des plasmonischen Buswellenleiters erreicht. Darüber hinaus kann das PIT-Fenster dynamisch durch Anpassen der geometrischen Parameter der Nanostruktur, wie beispielsweise der Lage und Breite der rechteckigen Nanokavität, abgestimmt werden. Im Vergleich zu den herkömmlichen Ringresonatoren [24, 25] bieten unsere vorgeschlagenen asymmetrischen U-förmigen und rechteckigen Resonatoren eine stärkere Kopplungsstärke zwischen den Resonatoren und dem Buswellenleiter, was weiter zu einem stärkeren PIT-Effekt führt. Auf der anderen Seite werden unsere Strukturen im Gegensatz zu anderen berichteten Nanobandwellenleitern durch die lokale Variation des chemischen Potenzials auf der identischen Graphen-Monoschicht gebildet, was eine einfachere Integration mit anderen funktionellen Komponenten auf derselben Materialplattform ermöglicht. Darüber hinaus kann diese plasmonische Nanostruktur als Brechungsindexsensor mit hoher Sensibilität verwendet werden. Und auch der langsame Lichteffekt mit großer Gruppenlaufzeit wird im PIT-System realisiert. Die vorgeschlagene Nanostruktur ebnet einen neuen Weg zur Realisierung von auf dem Chip integrierten nanophotonischen Geräten auf Graphenbasis.

Abkürzungen

CMT:

Theorie der gekoppelten Mode

EIT:

Elektromagnetisch induzierte Transparenz

FEM:

Finite-Elemente-Methode

PIT:

Plasmoneninduzierte Transparenz

RIU:

Brechungsindexeinheit

SPPs:

Oberflächenplasmonenpolaritonen