Einfluss des Substrats auf die Wellenlänge und Stärke der LSP-Kopplung

Hintergrund

Lokalisiertes Oberflächenplasmon (LSP) ist ein starkes Kopplungsphänomen zwischen Elektronen in Edelmetall-Nanopartikeln (NPs) und einfallendem Licht, wenn die Größe der NPs vergleichbar oder kleiner als die Wellenlänge des einfallenden Lichts ist. Die LSP-Resonanzwellenlänge hängt von der Größe, Form und dem Material der NPs sowie von der umgebenden dielektrischen Umgebung ab [1,2,3,4]. Aufgrund ihrer vielen attraktiven Eigenschaften, einschließlich exponentiell verstärkter elektrischer Felder in der Nähe der Grenzfläche zwischen Metall und dielektrischem Medium und einer verbesserten Absorption bei der Plasmonenresonanzwellenlänge [5, 6], wurden LSPs in viele optoelektronische Geräte integriert, einschließlich Leuchtdioden (LEDs ) [7,8,9], Photodetektoren [10, 11], Solarzellen [12, 13] und andere neue Technologien wie oberflächenverstärkte Raman-Streuung (SERS) [14,15,16,17], Spitzen- verbesserte Raman-Streuung (TERS) [18, 19] und chemische Sensoren [20, 21].

Für die meisten LSP-basierten Anwendungen sind Substrate, die die Metall-NPs unterstützen, unvermeidlich. In bisherigen Studien konzentrierten sich Untersuchungen zum Einfluss von Substraten meist auf den Brechungsindex von Substraten oder die Trennung zwischen Partikeln und Substraten [22, 23]. Insbesondere bei Metallnanopartikeln mit kubischer Geometrie werden Substrate die Hybridisierung zwischen dipolaren und quadrupolaren Würfelmoden induzieren [24, 25]. Der Einfluss von Substraten wird durch eine effektive Brechungsindextheorie vernachlässigt. In unserer früheren Arbeit haben wir jedoch die unterschiedlichen LSP-Kopplungsstärken diskutiert, wenn Licht aus verschiedenen Richtungen einfällt, wenn sich hemisphärische Metall-NPs auf einem Substrat befinden, was auf die unterschiedlichen lokalisierten elektrischen Feldstärken zurückzuführen ist, die von der Fresnel-Reflexion der Grenzfläche herrühren [26]. In dieser Arbeit werden drei Strukturen mit auf dem Substrat befindlichen Au-NPs für die FDTD-Simulation verwendet, um die Kopplungswellenlängen und die Stärke der LSPs zu diskutieren. Die erste Struktur sind halbkugelförmige Metall-NPs auf einem Substrat, die durch physikalische Methoden wie thermisches Tempern oder Nanoimprint erhalten werden können [27,28,29]. Die zweite Struktur sind kugelförmige Metall-NPs auf einem Substrat, die normalerweise durch chemische Synthese und anschließenden Übertragungsprozess erhalten werden [30, 31]. Diese beiden Strukturen werden typischerweise für ein festes Substrat verwendet. Die dritte Struktur sind kugelförmige Metall-NPs, die halb in das Substrat eingebettet sind und an einer Flüssig-Flüssig-Grenzfläche beobachtet wurden [32]. Unsere Ergebnisse zeigen, dass sich der effektive Brechungsindex des die NPs umgebenden Mediums für verschiedene Strukturen unterschiedlich verhält. Die Koppelwellenlängen der ersten und der dritten Struktur verschieben sich stark mit der Zunahme der Brechungsindizes des Substrats, während die Koppelwellenlänge der zweiten Struktur nahezu konstant bleibt. Dies kann auf verschiedene Grade des Eindringens des elektrischen Polarisationsfeldes in das Substrat zurückgeführt werden. Darüber hinaus wurden die LSP-Kopplungsstärken dieser drei Strukturen auch durch Einstellen der Richtung des einfallenden Lichts, normalerweise entweder von Luft oder Substrat, untersucht. Simulierte Ergebnisse zeigen, dass für die erste und zweite Struktur, wenn Licht aus unterschiedlichen Richtungen einfällt, das Verhältnis der Streupeakintensitäten gleich dem Verhältnis der Brechungsindizes des einfallenden Mediums und des austretenden Mediums ist. Für die dritte Struktur sind diese beiden Verhältnisse jedoch nicht gleich. Dieses Verhalten kann quantitativ erklärt werden, indem die lokalen treibenden elektrischen Feldstärken der LSPs unter Verwendung modifizierter Fresnel-Gleichungen betrachtet werden.

In der Praxis wird jedoch in der Regel eine Array-Struktur von Nanopartikeln zur Untersuchung erreicht. Daher wurden auch NP-Dimere [33,34,35] für die Diskussion verwendet, da die Nahfeldeigenschaften der periodischen NP-Strukturen durch Randbedingungsprobleme in FDTD-Simulationen beeinflusst werden. Die Ergebnisse der FDTD-Simulation zeigen, dass die Trends der Kopplungswellenlängen und -stärken der Metall-NP-Dimere größtenteils denen der Einzelmetall-NP für die erste und dritte Struktur ähnlich sind. Bei Metall-NP-Dimeren mit der zweiten Struktur ist der Einfluss des Brechungsindex des Substrats jedoch etwas stärker als bei Einzelmetall-NP.

Ergebnis und Diskussion

Abbildung 1a–c zeigen die schematischen Darstellungen der Strukturen für FDTD-Simulationen. Die in Fig. 1a gezeigte Struktur stellt die halbkugelförmigen Au-NPs auf einem dielektrischen Substrat dar, das als Struktur A bezeichnet wird. Die in Fig. 1b gezeigten Strukturen stellen die kugelförmigen Au-NPs auf einem dielektrischen Substrat dar, das als Struktur B bezeichnet wird. Zum Vergleich:die in Abb. 1c gezeigte Struktur C, die eine höhere Symmetrie aufweisen, wird auch für Simulationen verwendet. Zur Simulation werden die Durchmesser der Au-NPs für alle Strukturen auf 60 nm festgelegt. Die Brechungsindizes der Medien über den Substraten werden als n . festgelegt ₁ = 1 in den meisten Fällen. Die Brechungsindizes der Substrate variieren von n ₂ = 1 bis n ₂ = 2,5. Abbildung 1d–f zeigt die normierten Streuspektren der Strukturen A bzw. C. Es ist deutlich zu erkennen, dass sich für die Struktur A und C die Streupeaks mit zunehmendem Brechungsindex der Substrate stark rotverschieben. Für Struktur B hat die Erhöhung der Brechungsindizes der Substrate jedoch einen vernachlässigbaren Einfluss auf die Streupeaks.

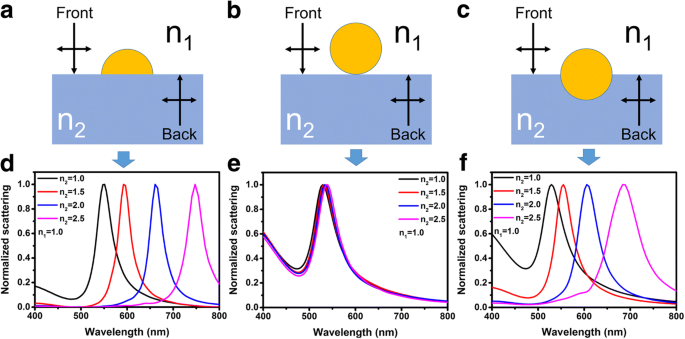
a –c Schematische Diagramme der Strukturen A bis C, die jeweils für FDTD-Simulationen verwendet werden. d –f Normalisierte Streuspektren der Struktur A bis C mit jeweils unterschiedlichen Substratbrechungsindizes

Abbildung 2a zeigt die Wellenlänge der LSP-Streuungsmaxima im Vergleich zu den Brechungsindizes der Substrate, die aus Fig. 1 extrahiert wurden. Aus Fig. 2a können wir als erste Information erhalten, dass, wenn die Brechungsindizes von Substraten zunehmen, die Wellenlängen der Streuungspeaks zunehmen schneller als die lineare Annahme. Dies kann näherungsweise durch die Mie-Theorie erklärt werden. Aus der Mie-Theorie unter der quasi-statischen Näherung der Streuquerschnitt eines Metall-NP, umgeben von einem isotropen und nicht absorbierenden Medium mit Dielektrizitätskonstante ε _m kann ausgedrückt werden als:

wo k ist der Wellenvektor der sich ausbreitenden Welle, a der Radius eines kugelförmigen Metall-NP ist und ε repräsentiert die Dielektrizitätskonstante des Metalls. Der Einschub in Fig. 2a zeigt die Beziehung zwischen den Streupeakwellenlängen und den Brechungsindizes des Mediums, das das Metall-NP umgibt, berechnet unter Verwendung von Gl. (1). Man kann deutlich die superlineare Beziehung zwischen den Streupeakwellenlängen und den Brechungsindizes sehen, die den simulierten Ergebnissen ziemlich ähnlich ist. Somit können wir die Theorie des effektiven Brechungsindex für weitere Diskussionen verwenden. Aus der Theorie des effektiven Brechungsindex, wenn die Streupeakwellenlängen von Au-NP von einem unendlichen dielektrischen Medium mit Brechungsindex n . umgeben sind _eff gleich dem des Au-NP für verschiedene Strukturen, n _eff können als effektive Brechzahlen der entsprechenden Strukturen angesehen werden. Tabelle 1 zeigt die n _eff mit dieser Methode erhalten.

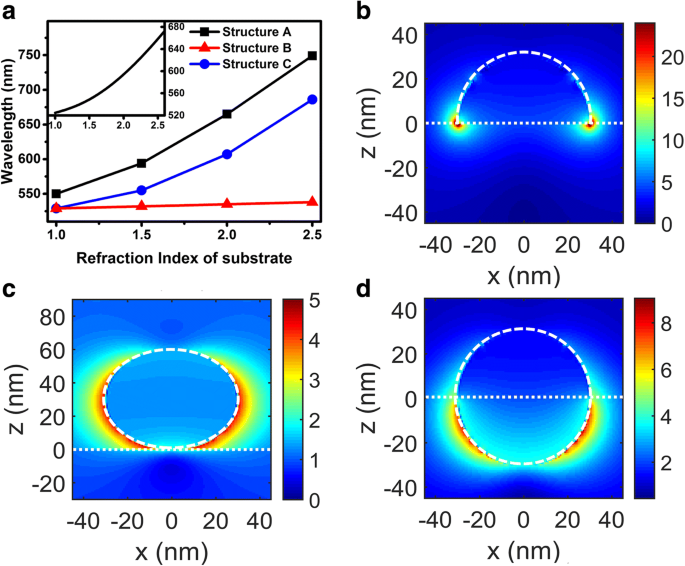
a Streuung von Spitzenwellenlängen verschiedener Strukturen mit unterschiedlichen Substratbrechungsindizes. Der Einsatz zeigt die Beziehung zwischen der LSP-Kopplungswellenlänge und dem Brechungsindex des umgebenden Mediums basierend auf der Mie-Theorie. b –d Polarisationsverteilungen des elektrischen Feldes der Struktur A bis C mit n ₂ = 1,5 jeweils bei der entsprechenden LSP-Kopplungswellenlänge

Verwenden einer linearen Anpassungsgleichung [36]:

wobei μ kann als Gewichtungskoeffizient angesehen werden, um den Einfluss des Substratbrechungsindex auf die LSP-Kopplungswellenlänge abzuschätzen. Der Einfluss der Medien oberhalb und unterhalb der Grenzfläche kann abgeschätzt werden. Unter Verwendung der in Tabelle 1 gezeigten Parameter werden die Gewichtungskoeffizienten μ der Struktur A bis C sind 0,38 ± 0,02, 0,93 ± 0,01 bzw. 0,25 ± 0,05. Diese Ergebnisse zeigen, dass für Struktur B die Wellenlänge des Streupeaks fast nur vom Brechungsindex des Mediums oberhalb der Grenzfläche abhängt. Für Struktur C spielt der Brechungsindex des Substrats eine wichtige Rolle für die Wellenlänge des Streupeaks. Bei Struktur A wird die Streuungspeakwellenlänge jedoch sowohl durch den Brechungsindex der Medien oberhalb als auch unterhalb der Grenzfläche beeinflusst.

Diese Phänomene können durch die Analyse der elektrischen Feldverteilungen erklärt werden. Abbildung 2b–d zeigt die Amplitudenverteilungen des elektrischen Felds der Struktur A bis C mit n ₂ =1,5 bei den entsprechenden Streupeakwellenlängen. Elektrische Felder, die hauptsächlich in der Nähe der Grenzfläche konzentriert sind, beeinflussen sowohl das Medium oberhalb der Grenzfläche als auch das Medium unterhalb der Grenzfläche die Resonanzwellenlängen der LSPs für die Strukturen A bis C. Diese Ergebnisse bestätigen, dass die Verteilung des elektrischen Felds gut mit den berechneten Gewichtungskoeffizienten übereinstimmt, da der Einfluss des umgebenden Mediums auf die Wellenlänge des Streupeaks auf die Polarisation des dielektrischen Mediums zurückzuführen ist, die durch das lokalisierte elektrische Feld verursacht wird.

Aus Gl. (2) erhalten wir, wenn n ₂ ist behoben und n ₁ abstimmbar ist, die Änderungsrate, d. h. die Steigung der n _eff , sind die Gewichtungskoeffizienten μ . Somit können wir die obigen Ergebnisse verwenden, um den LSP-basierten chemischen Sensor zu optimieren, wenn das Substrat unvermeidbar ist. LSP-basierter chemischer Sensor soll die Brechungsindexänderung der Umgebung durch die LSP-Resonanzpeak-Wellenlängenverschiebung Δλ . erkennen [37]. Die Empfindlichkeit der Sensoren hängt stark von zwei Parametern ab, darunter dem Verschiebungsparameter S = d (Δλ )/d (Δn ) und die Verdienstzahl FOM = S /FWHM , wobei Δn repräsentiert die Änderung des Brechungsindex und FWHM ist die Vollwelle beim Halbmaximum des Anfangszustandes [37, 38]. Die meisten früheren Studien zu LSP-basierten Sensoren konzentrieren sich auf das Material, die Größe und die Form der NPs [39,40,41]. Allerdings diskutierten nur sehr wenige Berichte den Einfluss des Substrats und deren Wechselwirkungen mit den Metall-NPs. Abbildung 3 zeigt die Streuspektren der Strukturen A bis C bei n ₁ wird linear von 1,0 auf 1,5 erhöht und n ₂ ist als 1,5 oder 2,5 festgelegt. Die in allen Abbildungen gezeigten Einsätze repräsentieren die Streupeakwellenlängen vs. n ₁ . Abbildung 3a–f zeigen, dass das S Parameter für Struktur A und B ist höher als der von Struktur C. Tabelle 2 listet die berechneten Parameter von S . auf , FWHM , und FOM aus Abb. 3. Für n ₂ = 1.5, das S und FOM Parameter für die Strukturen A und B ist viel besser als die von Struktur C. Für n ₂ = 2.5, obwohl das S Parameter für die Strukturen A und B ist höher als bei n ₂ = 1.5, das FOM verschlechtert sich aufgrund der Zunahme von FWHM .

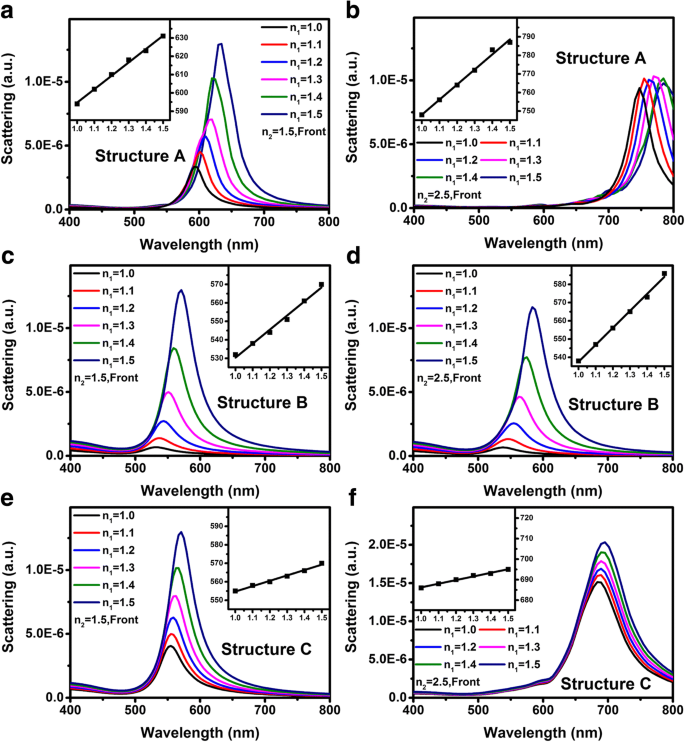
a , c , e Streuspektren der Struktur A bis C bei n ₁ wird linear von 1,0 auf 1,5 erhöht. mit festem n ₂ = 1,5 bzw. . b , d , f Streuspektren der Struktur A bis C bei n ₁ wird linear von 1,0 auf 1,5 erhöht, mit festem n ₂ =2,5, bzw.. Die Einschübe zeigen die Beziehung zwischen den Streupeakwellenlängen und n ₁ für unterschiedliche Strukturen oder Substratbrechungsindizes

Die obige Diskussion dreht sich alles um die LSP-Kopplungswellenlänge. Die LSP-Kopplungsstärke ist ein weiterer wertvoller Parameter für viele LSP-basierte Geräte wie LEDs, Fotodetektoren, Solarzellen und neue Techniken wie SERS, TERS und chemische Sensoren. Unsere vorherige Untersuchung zeigte, dass für Struktur A die Kopplungsstärke zwischen Licht und LSPs durch die Einfallsrichtung des Lichts beeinflusst wird. Dies kann auf die unterschiedlichen lokalen treibenden elektrischen Feldstärken zurückgeführt werden, wenn Licht normalerweise aus der Luft und dem Substrat einfällt [26]. Das Verhältnis der Extinktionspeakintensitäten bei Lichteinfall vom Substrat (bezeichnet als Rückeinfall) und der Luft (bezeichnet als Fronteinfall) C _B /C _F ist gleich n ₂ /n ₁ . Abbildung 4 zeigt die FDTD-simulierten Streuspektren bei Lichteinfall aus verschiedenen Richtungen in Verbindung mit den Streuspektren von Au-NPs, die von den entsprechenden effektiven Brechungsindizes umgeben sind. Abbildung 4a–c, d–f repräsentieren die Streuspektren der Strukturen A bzw. C. Die Brechungsindizes des Substrats n ₂ sind 1,5, 2,0 und 2,5 für Abb. 4a, d, b, e, c bzw. f. n ₁ ist für alle Spektren auf 1.0 festgelegt. Ähnlich wie bei den Extinktionsspektren sind die Streupeakintensitäten bei Lichteinfall von hinten und vorne C _SB /C _SF ist gleich n ₂ /n ₁ sowohl für Struktur A als auch für C.

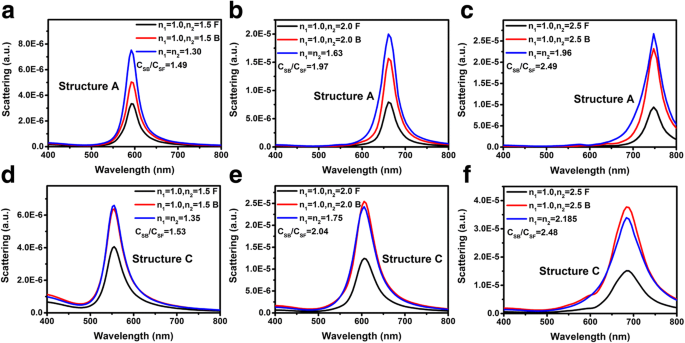
Streuspektren für variierende n ₂ = 1.5, 2.0 und 2.5 von Struktur A (a –c ) und Struktur C (d –f ) bzw. Licht fällt normalerweise von Luft (als schwarze Linien bezeichnet) und Substraten (als rote Linien bezeichnet) ein. Die blauen Linien zeigen die Streuspektren, bei denen die Au-NPs von unendlichen dielektrischen Medien mit effektiven Brechungsindizes umgeben sind

Berücksichtigt man die Streuspektren von Au-NPs, die von den entsprechenden effektiven Brechungsindizes umgeben sind, gibt es Unterschiede zwischen den Streupeakintensitäten der Struktur A und C. Abbildung 5a, b zeigen die Verhältnisse von C _SF /C _Seff und C _SB /C _Seff gegenüber den Brechungsindizes der Substrate der Struktur A bzw. C, wobei C _Seff ist die Streuungspeakintensität, bei der die Au-NPs von unendlichen dielektrischen Medien mit effektiven Brechungsindizes umgeben sind (Abb. 4). Für alle Substrate gelten die Verhältnisse C _SF /C _Seff und C _SB /C _Seff der Struktur A sind kleiner als die der Struktur C. Dies kann auch durch den Unterschied zwischen dem lokalen treibenden elektrischen Feld von Struktur A und C erklärt werden.

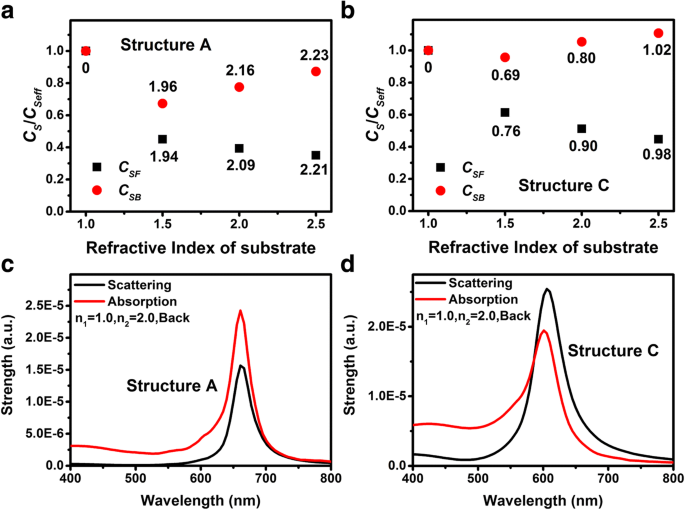
a , b Die Verhältnisse der Kopplungsstärken C _S /C _Seff mit verschiedenen n ₂ von Struktur A bzw. Struktur C. Schwarze rechteckige und rote kreisförmige Punkte repräsentieren die vorderen bzw. hinteren Vorfallfälle. c , d Streu- und Absorptionsspektren der Strukturen A und C mit festem n ₂ = 2.0 wenn Licht vom Substrat einfällt

Basierend auf den modifizierten Fresnel-Gleichungen [26, 42] kann die Intensität des lokalen treibenden elektrischen Felds bei Lichteinfall von der Vorder- und Rückseite als 2n . geschrieben werden ₁ E _ich /(n ₁ + n ₂ + A ) und 2n ₂ E _ich /(n ₁ + n ₂ + A ), wobei E _ich die elektrische Feldstärke der einfallenden Welle ist und A =  − i (ω /c )ρα kann als zusätzlicher Parameter angesehen werden, der sich aus den LSPs ergibt, der proportional zur Polarisierbarkeit α . ist der Au-NPs und ist eine positive reelle Zahl bei der LSP-Resonanzfrequenz. Somit ist das C _SB /C _SF ist gleich n ₂ /n ₁ was auch in Abb. 4 dargestellt ist. Andererseits ist die lokale treibende elektrische Feldstärke, wenn die Au-NPs von dem entsprechenden effektiven Brechungsindex umgeben sind, gleich E _ich . Somit ist der Wert von A Parameter kann mit der Gleichung erhalten werden:

Das berechnete A Parameter sind in der Nähe des entsprechenden Punktes in Abb. 5a, b aufgelistet. Man sieht, dass der Wert von A ist sehr nahe, aber für verschiedene Lichteinfallsrichtungen nicht genau gleich. Dies wird auf den leichten Unterschied zwischen C . zurückgeführt _SB /C _SF und n ₂ /n ₁ sowie die Genauigkeit der Simulationssoftware. Für dieselbe Struktur mit unterschiedlichen Substratbrechungsindizes beträgt der A Wert steigt mit steigendem Brechungsindex des Substrats, was auf die erhöhte Polarisierbarkeit der Au-NPs mit steigender LSP-Resonanzwellenlänge zurückgeführt werden kann [43,44,45]. Andererseits sollte man sich bewusst sein, dass die A Wert von Struktur A ist viel größer als der von Struktur C für verschiedene Strukturen mit gleichen Substratbrechungsindizes. Dies bedeutet, dass die Polarisierbarkeit der Au-NPs für Struktur A viel größer ist als die von Struktur C, was in Abb. 2b, d nachgewiesen werden kann. Es ist interessant, dass, obwohl die Polarisierbarkeit der Au-NPs von Struktur A größer ist als die von Struktur C, die Streupeakintensitäten von Struktur A geringer sind als die von Struktur C (Abb. 4). Dies ist auf die höhere Absorption von Struktur A zurückzuführen. Abbildung 5c, d zeigt die Streu- und Absorptionsspektren von Struktur A bzw. C, der Brechungsindex des Substrats beträgt für beide Strukturen 2,0 und das Licht fällt von der Rückseite ein. Man kann sehen, dass die Absorption von Struktur A viel höher ist als die von Struktur C. Somit wird für Struktur A die meiste Energie, die die LSPs anregt, durch Absorption verbraucht und nicht gestreut.

Für Struktur B gilt jedoch das Verhältnis C _SB /C _SF ist nicht gleich n ₂ /n ₁ . Abbildung 6a–c zeigt die Streuspektren der Struktur B mit unterschiedlichen Substratbrechungsindizes von 1,5, 2,0 bzw. 2,5. C _SB /C _SF der Struktur B ist kleiner als n ₂ /n ₁ für alle Substratbrechungsindizes. Wie in Fig. 6d schematisch dargestellt, kann das lokale elektrische Antriebsfeld, wenn Licht von der Vorderseite einfällt, als Überlagerung von E . geschrieben werden _ich und E _rF , wobei E _rF ist die elektrische Feldstärke der reflektierten Welle. Die lokale treibende elektrische Feldstärke bei Lichteinfall von der Vorderseite kann geschrieben werden als \( {E}_{dF}={E}_i+{E}_{rF}=\left[1+\frac{n_1- {n}_2}{n{}_1+{n}_2}\cos\left(\frac{4\pi Pa}{\lambda_{LSP}}\right)\right]{E}_i\), wobei P ist ein Koeffizient, der sich auf den durchschnittlichen Abstand der oszillierenden Elektronen und einen zusätzlichen Lichtweg bezieht, wenn sich Licht durch die Au-NPs ausbreitet, und der λ _LSP ist die Resonanzwellenlänge der LSPs. In Anbetracht dessen, dass die lokale treibende elektrische Feldstärke bei Lichteinfall von der Rückseite als E . geschrieben werden kann _dB = E _tB = 2n ₂ E _ich /(n ₁ + n ₂ ), kann das Verhältnis der lokalen treibenden elektrischen Feldstärken bei Lichteinfall von der Vorder- und Rückseite wie folgt geschrieben werden:

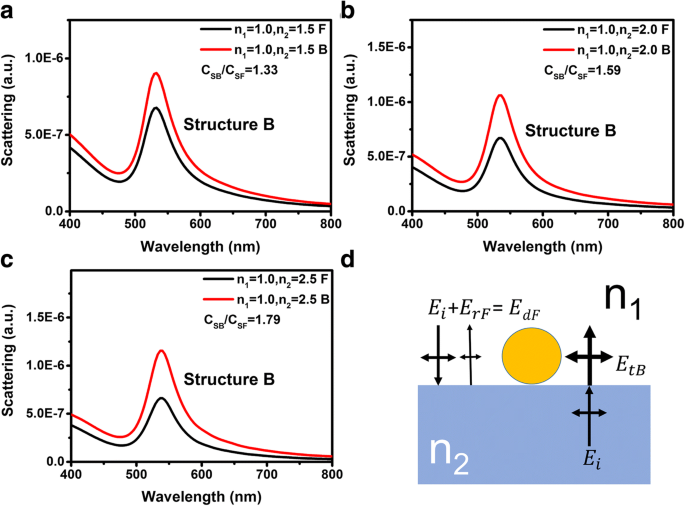
a –c Streuspektren für variierende n ₂ = 1,5, 2,0 bzw. 2,5 der Struktur B. Schwarze und rote Linien repräsentieren jeweils die vorderen und hinteren Vorfallfälle. d Schematische Darstellung des lokalen elektrischen Antriebsfeldes der Struktur B für verschiedene Einfallsrichtungen

In Tabelle 3 sind die C . aufgeführt _SB /C _SF der Struktur B erhalten durch die Streuspektren und die E _dB /E _dF berechnet nach Gl. (4) mit verschiedenen P Koeffizienten. Das sieht man, wenn das P Koeffizient gleich 1,5, E _dB /E _dF stimmt gut mit den Verhältnissen von C . überein _SB /C _SF für alle Untergründe. Der Grund, warum P gleich 1,5 ist noch unklar.

In den Tabellen 4 und 5 sind die C . aufgeführt _SB /C _SF erhalten durch die Streuspektren und das E _dB /E _dF berechnet nach Gl. (4) für NPs mit unterschiedlichen geometrischen Strukturen und Materialien, um die Universalität des P . zu untersuchen Koeffizient. Dies kann man für Au-NPs mit unterschiedlichen Größen sehen, wenn das P Koeffizient gleich 1,5, die Verhältnisse von C _SB /C _SF und E _dB /E _dF stimmen recht gut überein, wenn die NPs abgeflacht elliptisch oder gestreckt elliptisch sind. Tabelle 5 zeigt, dass die P Koeffizient der Ag-NPs mit unterschiedlicher Größe beträgt ebenfalls 1,5. Somit ist das P Koeffizient ist relativ universell, was darauf hindeutet, dass es einen internen Mechanismus für das P . geben sollte Koeffizient und eine eingehendere Untersuchung wert.

Die obigen Diskussionen basieren auf einzelnen NP. In der Praxis werden jedoch meist Array-Strukturen von Nanopartikeln zur Untersuchung erreicht. Daher sollten NP-Dimere zur Diskussion verwendet werden, da die Nahfeldeigenschaften der periodischen NP-Strukturen durch Randbedingungsprobleme in FDTD-Simulationen beeinflusst werden. Die geometrischen Strukturparameter der für die Dimersimulation verwendeten NPs ähneln denen für das oben diskutierte einzelne NP, und zwischen diesen beiden NPs wird eine Lücke von 2 nm festgelegt. Die simulierten Ergebnisse (hier nicht gezeigt) zeigten, dass, wenn die Polarisationsrichtung von normal einfallendem Licht senkrecht zum NP-Dimer verläuft, alle Eigenschaften dieselben sind wie für einzelne NP. Somit basieren alle unten diskutierten Nahfeldeigenschaften auf einfallendem Licht, dessen Polarisationsrichtung parallel zum NP-Dimer ist.

Abbildung 7a, b zeigen die schematischen Darstellungen von halbkugelförmigen Au-Dimeren auf einem dielektrischen Substrat (Struktur A′) bzw. kugelförmigen Au-Dimeren, die halb in das Substrat eingebettet sind (Struktur C′). Abbildung 7c, d zeigt die Streuspektren der Dimere mit unterschiedlichen Substratbrechungsindizes und Lichteinfallsrichtungen. Man sieht, dass für die Struktur A′ und C′ in allen Spektren sowohl die Streupeaks erster als auch zweiter Ordnung beobachtet werden. Insbesondere für die Struktur C&sub1; können die Peaks dritter Ordnung beobachtet werden, wenn die Brechungsindizes des Substrats gleich 2 und 2,5 sind. Es ist auch zu erkennen, dass sich alle Streupeaks mit zunehmendem Brechungsindex des Substrats stark rot verschieben. Dies kann durch die Amplitudenverteilungen des elektrischen Felds bei den entsprechenden Wellenlängen des Peaks erster Ordnung für die Struktur A′ und C′ erklärt werden, wie in Fig. 8a bzw. b gezeigt, wobei die Brechungsindizes des Substrats 1,5 betragen. Ähnlich wie in 2 gezeigt, konzentrierte sich das elektrische Feld hauptsächlich in der Nähe der Grenzfläche. Wenn Licht aus verschiedenen Richtungen einfällt, ist also C _SB /C _SF zu n ₂ /n ₁ erwartet werden kann und wie in Abb. 7c, d. Andererseits sind im Vergleich zu den in Fig. 4 gezeigten Streuspektren die Streupeakintensitäten des Dimers viel höher als die des einzelnen NP. Dies wird auf die starke Verstärkung des elektrischen Felds durch die Hot Spots zurückgeführt an den Nanolücken [33].

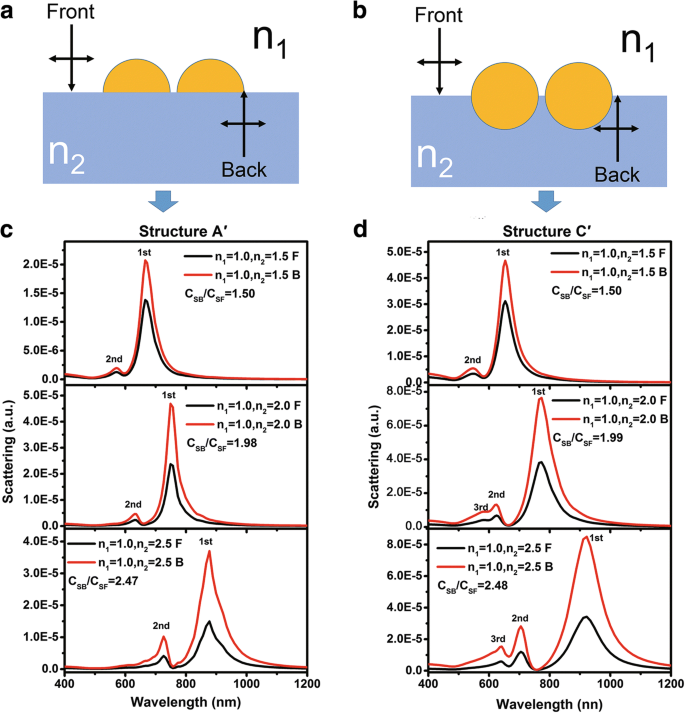
a , b Schematische Diagramme der Struktur A′ und C′, die jeweils für FDTD-Simulationen verwendet werden. c , d Streuspektren für variierende n ₂ = 1,5, 2,0 und 2,5 der Struktur A′ bzw. der Struktur C′. Licht fällt normalerweise von Luft (als schwarze Linien gekennzeichnet) und Substraten (als rote Linien gekennzeichnet) ein.

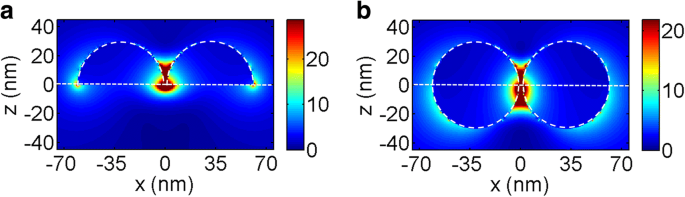
a , b Polarisationsverteilungen des elektrischen Feldes der Struktur A′ und C′ mit n ₂ = 1.5 bei den entsprechenden Wellenlängen des Peaks erster Ordnung bzw.

Wie jedoch in Abb. 9 gezeigt ist, ist der Einfluss des Brechungsindex des Substrats für kugelförmige Au-Dimere, die sich auf einem dielektrischen Substrat (Struktur B′) befinden, etwas stärker als bei Struktur B. Die Rotverschiebung des Peaks erster Ordnung von 580 auf 614 nm, wenn der Brechungsindex des Substrats von 1,5 auf 2,5 erhöht wird, was größer ist als der für einzelne NP (von 532 auf 538 nm). Dies kann den Amplitudenverteilungen des elektrischen Felds bei der entsprechenden Peakwellenlänge des Peaks erster Ordnung für die Struktur B&sub1; zugeschrieben werden (Fig. 9d, der Brechungsindex des Substrats beträgt 1,5). Die elektrische Feldstärke im Substrat ist stärker als die in Fig. 2c gezeigte. Außerdem ist, wie in Abb. 9 gezeigt, das Verhältnis von C _SB /C _SF für NP-Dimere der Struktur B′ ungleich n ₂ /n ₁ , ähnlich dem für einzelne NP. Die P Parameter ist keine Konstante mehr, wenn Gl. (4) wird weiterhin angewendet. Das P Parameter können zu 1,67, 1,82 und 2,05 berechnet werden, wenn der Brechungsindex des Substrats 1,5, 2,0 bzw. 2,5 beträgt. Der Unterschied zwischen dem P Parameter für Struktur B und B′ bedarf weiterer Untersuchungen.

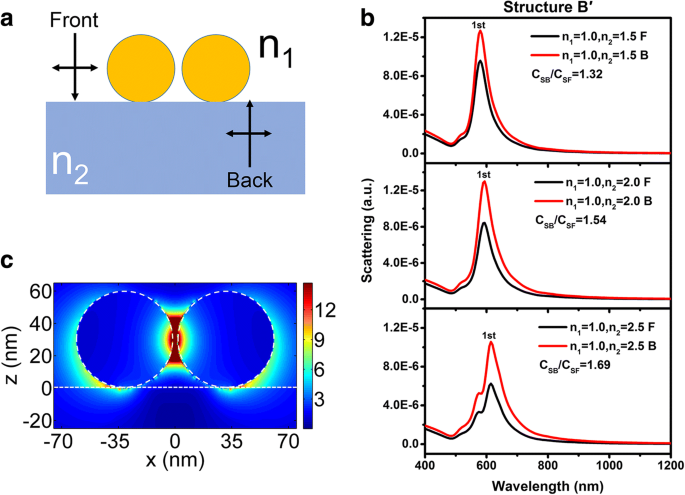
a Schematische Diagramme der Struktur B′, die für FDTD-Simulationen verwendet wird. b Streuspektren für variierende n ₂ = 1,5, 2,0 und 2,5 der Struktur B′. Licht fällt normalerweise von Luft (als schwarze Linien bezeichnet) und Substraten (als rote Linien bezeichnet) ein. c Polarisationsverteilungen des elektrischen Feldes der Struktur B′ mit n ₂ = 1,5 bei 532 nm

Schlussfolgerungen

Zusammenfassend wurde der Einfluss des Substrats auf die Kopplungswellenlänge und -stärke von LSPs durch FDTD-Simulation und theoretische Analyse untersucht. Bei den Strukturen mit halbkugelförmigen Au-NPs auf dem Substrat und sphärischen Au-NPs, die halb in das Substrat eingebettet sind, variiert die LSP-Kopplungswellenlänge stark mit dem Brechungsindex des Substrats. Allerdings ist die Abhängigkeit der LSP-Kopplungswellenlänge vom Substrat für die Struktur, bei der sich sphärische Au-NPs auf dem Substrat befinden, marginal. Der Abhängigkeitsunterschied wurde durch die Polarisationsfeldverteilungen von LSPs für verschiedene Strukturen erklärt. Bei der Struktur, bei der sphärische Au-NPs halb in das Substrat eingebettet sind, konzentriert sich das Polarisationsfeld von LSPs im Medium über dem Substrat. Bei den anderen beiden Strukturen dringen die Polarisationsfelder jedoch stark in das Substrat ein. Darüber hinaus wurden die LSP-Kopplungsstärken dieser drei Strukturen auch durch Ändern der Einfallsrichtung des Lichts, entweder normalerweise von Luft oder Substrat, untersucht. Simulierte Ergebnisse zeigen, dass für die Strukturen mit hemisphärischen NPs auf dem Substrat und sphärischen NPs, die halb im Substrat eingebettet sind, das Verhältnis der Streupeakintensitäten für verschiedene Lichteinfallsrichtungen gleich dem Verhältnis der Brechungsindizes des einfallenden Mediums und das austretende Medium. Für die Struktur, bei der sich kugelförmige NPs auf dem Substrat befinden, sind diese beiden Verhältnisse jedoch nicht gleich. Diese Phänomene wurden quantitativ erklärt, indem die lokalen treibenden elektrischen Feldstärken der LSPs unter Verwendung modifizierter Fresnel-Gleichungen betrachtet wurden. Die Nahfeldeigenschaft von NP-Dimeren wird ebenfalls berechnet. Obwohl in den Streuspektren Peaks mehrerer Ordnungen gezeigt werden, verschieben sich die Streupeakwellenlängen für Strukturen mit Substratbrechungsindizes für halbkugelförmige Au-Dimere, die sich auf dem Substrat befinden, und sphärische Au-Dimere, die halb im Substrat vergraben sind, stark rot. Das Verhältnis der Streuspitzenintensitäten für verschiedene Lichteinfallsrichtungen ist gleich dem Verhältnis der Brechungsindizes des einfallenden Mediums und des austretenden Mediums. However, for Au dimers located on the substrate, the influence induced by the refractive index of the substrates is slightly stronger than that for single spherical Au NP located on the substrate.

Methods

The models of hemi-/spherical metal NP located on substrate (denoted as structures A and B) and spherical metal NP half-buried into substrate (denoted as structure C) are created and studied by Lumerical FDTD (version 8.15.736), a commercial finite-difference time-domain solver. The substrate is semi-infinite in the z axis and infinite in the x /y Achse. The size of NP is set as 60 nm in diameter. The refractive index parameter of metal, gold, and silver specifically are support by CRC [46]. Total-field scattered-field source (TFSF), a special designing light source for studying particle scattering, is adopted in our research. The light normally incident from + z direction (designed as front incident) and − z direction (designed as back incident). Perfectly matched layers (PMLs) were used to absorb the scattered radiation in all directions (in order to eliminate reflection back to the model). The PML parameters such as Kappa, Sigma, layers, and polynomial order are assumed by 2, 1, 32, and 3 respectively. In addition, FDTD method consists in introducing a space and time mesh that must satisfy the stability criterion [47]. In order to converge, the simulation time and time steps (dt) are set to 2000 fs and 0.07 fs respectively. The space mesh is set to 0.3 nm in every direction (dx  = dy  = dz ).

Abkürzungen

FDTD:

Zeitbereich mit endlicher Differenz

LSP:

Localized surface plasmon

NPs:

Nanopartikel

SERS:

Surface-enhanced Raman scattering

TERS:

Tip-enhanced Raman scattering

TFSF:

Gesamtfeld-Streufeld