Verbesserte hohe Leistung eines Metaoberflächen-Polarisators durch numerische Analyse der Degradationseigenschaften

Hintergrund

Die Kontrolle von Licht auf der Nanoskala wurde in der Nanooptik und Nanophotonik umfassend untersucht. Als Ergebnis wurden bisher verschiedene Arten von photonischen Nanostrukturen vorgeschlagen. Beispielsweise können die Nanohohlräume des photonischen Kristalls (PhC) mit ultrahohen Qualitätsfaktoren (Q) [1] Licht auf einen Subwellenlängenbereich beschränken. Ähnlich wie bei den PhC-Kavitäten werden hohe Q-Faktoren durch Mikroscheiben- [2, 3], sphärische [4] und trioidale [5] Hohlräume realisiert. Diese Kavitäten mit hohen Q-Faktoren bestehen normalerweise aus transparenten dielektrischen Materialien. Im Gegensatz zu diesen dielektrischen Hohlräumen haben metallische Hohlräume niedrige Q-Faktoren, können aber ihre gesamten Hohlraumgrößen reduzieren. Insbesondere plasmonische Hohlräume im Subwellenlängenbereich sind wichtig für die Kontrolle von Licht in extrem kleinem Maßstab [6]. Obwohl plasmonische Hohlräume niedrige Q-Faktoren haben, können sie Licht in einen tiefen Subwellenlängenbereich quetschen [7]. Dieses extrem begrenzte Licht wird voraussichtlich ein Schlüssel zur Verschmelzung von Photonik und Elektronik sein [8].

Neben den oben erwähnten photonischen Nanostrukturen haben Metaoberflächen in letzter Zeit erhebliche Aufmerksamkeit für das Design hochfunktioneller und ultradünner optischer Bauelemente auf sich gezogen. Es gibt verschiedene Arten von Metaoberflächen, die Brechung [9], Reflexion [10], Photolumineszenz [11], Fluoreszenz [12–14], Wellenplatten [15] und Strahlteiler [16] steuern. Der Polarisationszustand ist eine der grundlegenden und wichtigen Eigenschaften von Licht, die durch Metaoberflächen gesteuert werden kann [17–22]. Numerische und experimentelle Studien haben gezeigt, dass ein Metaoberflächen-Polarisator mit einer gestapelten komplementären Struktur ein hohes Extinktionsverhältnis in der Größenordnung von 10.000 im nahen Infrarotbereich aufweist [23–26]. Die komplementären Strukturen haben aufgrund des Babinet-Prinzips Resonanzen bei nahezu derselben Wellenlänge [27, 28]. Wenn eine komplementäre Struktur in Resonanz ist, die eine hohe Durchlässigkeit für eine bestimmte Polarisation zeigt, ist die andere Struktur außer Resonanz, die eine niedrige Reflexion für dieselbe Polarisation zeigt. Als Ergebnis weist die gesamte Struktur eine hohe Durchlässigkeit auf. Bei der orthogonalen Polarisation tauscht sich die Rolle der elektrischen und magnetischen Felder aus, was zu einem hohen Reflexionsgrad führt. Somit weist die Metaoberfläche mit komplementären Strukturen ein hohes Extinktionsverhältnis auf. Es gibt jedoch große Bedenken hinsichtlich der Stabilität und Zuverlässigkeit dieser hohen Leistung, da die Metaoberfläche Silber enthält, das in der Atmosphäre abgebaut wird. Um dieses Problem zu umgehen, besteht ein alternativer Ansatz darin, Gold als plasmonisches Material zu verwenden, aber dies verringert die Leistung des Polarisators aufgrund des erhöhten Metallverlusts. Daher sollte für praktische Anwendungen die Stabilität und Zuverlässigkeit des Metaoberflächen-Polarisators berücksichtigt werden.

In dieser Studie untersuchen wir die Degradationseigenschaften des Metasurface-Polarisators. Wir zeigen, dass das Extinktionsverhältnis des Polarisators eine zeitliche Verschlechterung zeigt. Als Ursache der Degradation konzentrieren wir uns auf den Einfluss der Oberflächenmorphologie auf die hohe Leistung des Polarisators. Um die Morphologie zu beschreiben, führen wir zwei Modelle ein. Eine beschreibt die Oberflächenrauheit durch eine periodische Kurve mit einem Gaußschen weißen Rauschen, während die andere die Rauheit durch die Verwendung zufällig verteilter Nanopartikel beschreibt. Wir haben auch die Auswirkung von Metallverlusten auf die hohe Leistung untersucht. Während dieser numerischen Berechnungen enthüllen wir einen entscheidenden Faktor, der die Verschlechterung verursacht, und schlagen einen optimierten Metaoberflächen-Polarisator mit einem hohen Extinktionsverhältnis vor.

Methoden/Experimental

Der experimentelle Aufbau für die Messung des hohen Extinktionsverhältnisses ist in Abb. 1 schematisch dargestellt Quelle. Die Pulsbreite und Repetitionsrate betrugen 7 ns bzw. 20 Hz. Das Idlerlicht des OPO wurde durch eine Linse auf die Probe fokussiert und durch ein Glan-Laser-Prisma (GLP) linear polarisiert. Das durchgelassene Idlerlicht wurde mit einem erweiterten InGaAs-Photodetektor (Edmund Optics) gemessen. Bei diesem optischen System verursacht die Fluktuation der Lichtintensität eines einzelnen Pulses ein schlechtes Signal-Rausch-Verhältnis (S/N). Um den Effekt dieser Fluktuation zu beseitigen, haben wir daher die mittlere Transmission eines einzelnen Pulses gemessen. Um die Lichtintensität eines einzelnen Pulses zu überwachen, haben wir ein Paar Beam Sampler zwischen die Linse und das GLP eingefügt. Ein Teil des Idlerlichts wurde am zweiten Strahlabtaster (BS2) reflektiert und dann wieder am reflektierenden Neutraldichtefilter (ND) reflektiert, der die reflektierte Laserintensität so einstellte, dass ein Photodetektor nicht beschädigt wurde. Der abgestimmte Laser traf auf einen erweiterten InGaAs-Photodetektor (Edmund Optics) durch eine Lochblende, die unnötiges „Geisterlicht“, das an der Rückseite des BS2 reflektiert wurde, blockierte (siehe Einschub von Abb. 1). Der erste Strahlabtaster dient als Kompensator der Abweichung des Strahlengangs.

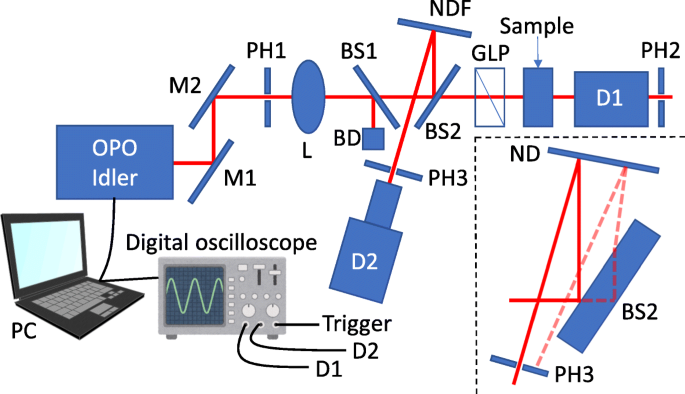
Schematische Darstellung des experimentellen Aufbaus der Extinktionsverhältnismessung. M Spiegel, PH Lochblende, L Linse, BS Beam Sampler, BD Beam Damper, NDF Neutral Density Filter, GLP Glan-Laser Prisma, D Detektor

Unter Verwendung dieses Aufbaus haben wir das Extinktionsverhältnis wie folgt bewertet. Das übertragene Signal wird zu D . berechnet ₁ =(1−R _BS2 )T _GLP T _Beispiel Ich , wobei R _BS2 , T _GLP , T _Beispiel , und ich sind das Reflexionsvermögen des BS2, das Transmissionsvermögen des GLP, das Transmissionsvermögen der Probe bzw. die Lichtintensität vor dem BS2. Die Signalintensität des Detektors 2 wird zu D . berechnet ₂ =R _BS2 R _NDF Ich , wobei R _NDF ist das Reflexionsvermögen des reflektierenden ND-Filters. Beachten Sie, dass die Lichtintensität ausreichend verringert wird, damit das erfasste Signal proportional zur Lichtintensität ist. Verwenden von D ₁ und D ₂ , können wir T . berechnen _Beispiel als

Um T auszuwerten _Beispiel , müssen wir auch das Reflexions- und Transmissionsvermögen der optischen Elemente, wie des Beam Samplers, messen. Dies ist unnötig, da unser Fokus auf einem Extinktionsverhältnis liegt, nämlich dem Verhältnis der Transmission. Indem wir die Probe um 90° drehen und die Transmission mit dem gleichen Setup messen, können wir einfach das Extinktionsverhältnis η . erhalten als

wobei die hochgestellten Buchstaben H und L die Polarisationszustände angeben, die eine hohe bzw. niedrige Durchlässigkeit aufweisen. In diesem Papier haben wir das Verhältnis D . gemessen ₁ /D ₂ für die orthogonalen Polarisationszustände und bewertet das Extinktionsverhältnis η .

Um die Validität der gemessenen Daten zu bestätigen, führten wir numerische Berechnungen auf der Grundlage der rigorosen gekoppelten Wellenanalyse (RCWA) mit der Streumatrixmethode [29, 30] und einer inversen Fouriermethode [31] durch. Die Permittivitäten von Ag und Siliciumdioxid wurden aus [32] bzw. [33] erhalten. Die Anzahl der reziproken Gittervektoren, die in der Berechnung verwendet wurden, betrug 2601.

Zur Berechnung der Transmission grober metallischer Strukturen haben wir eine kommerzielle Software von COMSOL Multiphysics verwendet, die auf der Finite-Elemente-Methode basiert. In der vorherigen Studie [34] wurden die Auswirkungen der Rauheit auf das optische Verhalten durch die Zunahme des Imaginärteils der Permittivität von Metall beschrieben. In dieser Arbeit haben wir neben der Erhöhung des Metallverlustes auch die direkten Auswirkungen von Gefügeänderungen gefolgt von der Rauheit auf den Transmissionsgrad betrachtet. Wir haben diese beiden Effekte getrennt behandelt. Wenn wir nur die Auswirkungen der Strukturänderungen berücksichtigen, haben wir die Volumenpermittivität auf metallische Strukturen mit Rauhigkeit angewendet. Wenn wir andererseits nur die Auswirkungen des erhöhten Verlusts betrachten, haben wir die modifizierte Permittivität auf metallische Strukturen ohne Rauheit angewendet. Wir setzen die relative Toleranz der numerischen Berechnungen auf weniger als 1%.

Ergebnisse und Diskussion

Abbildung 2a zeigt das Schema des dreischichtigen Metaoberflächen-Polarisators. Die erste Schicht hat eine komplementäre Struktur zur dritten Schicht (siehe Fig. 2b), wobei beide Schichten Silber (Ag) enthalten. Die zweite Schicht und das Substrat bestehen aus Siliziumdioxid (SiO₂ ). Wie in Abb. 1c gezeigt, weist die Metaoberfläche ein Array eines rechteckigen Lochpaares (150 nm ×  540 nm) auf und hat eine Periode von 900 nm im x und y Richtungen. Die Dicken der metallischen und dielektrischen Schichten betragen 45 bzw. 200 nm (siehe Abb. 2d). Die Probe wurde durch Nanoimprint-Lithographie in Verbindung mit anschließenden Trockenätztechniken hergestellt [35]. Die Details der Probenvorbereitung sind in [26] beschrieben. Abbildung 3 zeigt die rasterelektronenmikroskopischen (REM) Aufnahmen der präparierten Probe.

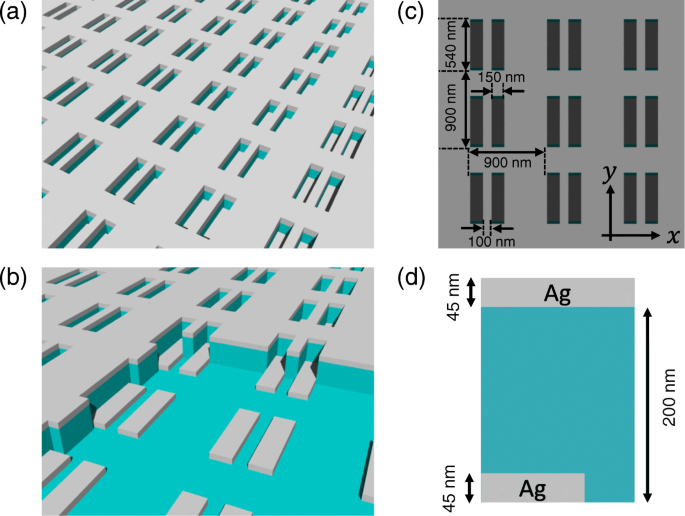
Ein Schema des Metaoberflächen-Polarisators (a ), die aus drei Schichten besteht (b ). Die Metaoberfläche hat ein Array von rechteckigen Lochpaaren mit einer Periode von 900 nm im x und y Wegbeschreibung (c ). Die Dicken der metallischen und dielektrischen Schichten betragen 45 bzw. 200 nm (d )

Das REM-Bild von a der Metaoberflächen-Polarisator und b sein vergrößertes Bild

Wir haben ein Spektrophotometer (V-7200, JASCO, Japan) verwendet, um die Transmission der Probe für das x . zu messen und y Polarisationen. Abbildung 4 zeigt die Messergebnisse. Die blauen und grünen Linien geben die Durchlässigkeit für das x . an und y Polarisationen bzw. Die blaue Linie, die der hohen Transmission entspricht, wird mit einem hohen S/N-Verhältnis gemessen. Die grüne Linie, die der geringen Durchlässigkeit entspricht, leidet jedoch unter einem niedrigen S/N-Verhältnis, was anzeigt, dass der Polarisator ein hohes Extinktionsverhältnis hat. Insbesondere die grüne Linie weist bei Wellenlängen über 1350 nm negative Signale auf, da die Intensität des durchgelassenen Lichts unter dem Rauschpegel des Spektralfotometers liegt. Daher haben wir das im vorherigen Abschnitt beschriebene optische System verwendet, um das hohe Extinktionsverhältnis zu messen.

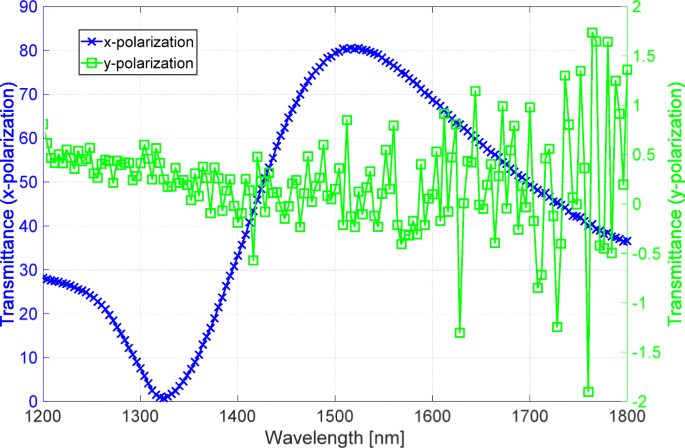
Transmissionsspektren, gemessen mit dem Spektrophotometer. Die blauen und grünen Linien sind die Spektren für das x und y Polarisationen bzw.

Abbildung 5a zeigt die gemessenen Transmissionsspektren für das x und y Polarisationen. Die blaue Linie, die der hohen Transmission entspricht, hat ein ähnliches Spektralprofil wie die vom Spektralfotometer gemessene Transmission. Die der geringen Transmission entsprechende grüne Linie weist um die Wellenlänge von 1625 nm einen deutlichen Einbruch auf, der vom Spektralphotometer nicht gemessen wurde. Durch Teilen der Transmission für das x Polarisierung dadurch für das y Polarisation bewerteten wir das in Abb. 5b gezeigte Extinktionsverhältnisspektrum. Das Extinktionsverhältnisspektrum hat einen Spitzenwert von über 20.000 um die Wellenlänge von 1640 nm.

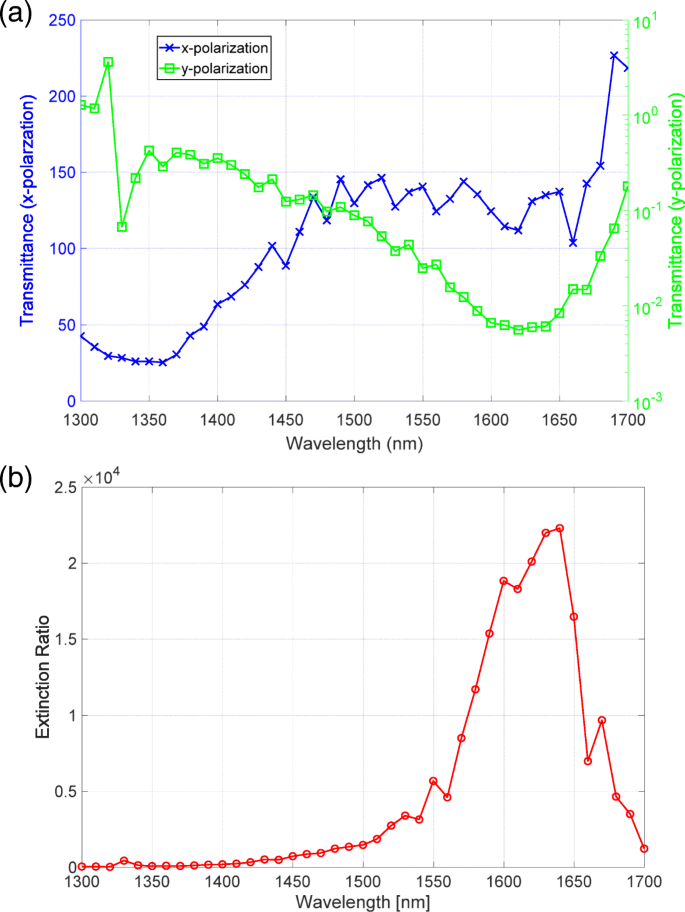
a Transmissionsspektren für das x (blau) und y (grün) Polarisationen gemessen mit dem in Abb. 1 gezeigten Aufbau. b Das Extinktionsverhältnisspektrum des Metaoberflächen-Polarisators

Um die Validität der Messdaten zu prüfen, haben wir die gemessenen Spektren mit den numerischen Berechnungsergebnissen verglichen. Wie in Fig. 6a gezeigt, stimmte das Spektrum mit hoher Durchlässigkeit mit den Spektren überein, die mit dem Spektrophotometer gemessen wurden. Das in einer logarithmischen Skala dargestellte niedrige Transmissionsspektrum weist einen deutlichen Einbruch um die Wellenlänge von 1640 nm auf. Dieses Merkmal stimmte gut mit dem im beobachteten Spektrum überein. Das in Fig. 6b gezeigte Extinktionsverhältnisspektrum hat einen Spitzenwert von 15.000, was nahe am beobachteten Wert liegt. Somit stimmten die gemessenen Transmissions- und Extinktionsverhältnisspektren mit den Ergebnissen der numerischen Berechnung überein, was darauf hindeutet, dass wir erfolgreich das hohe Extinktionsverhältnis von über 20.000 beobachtet haben.

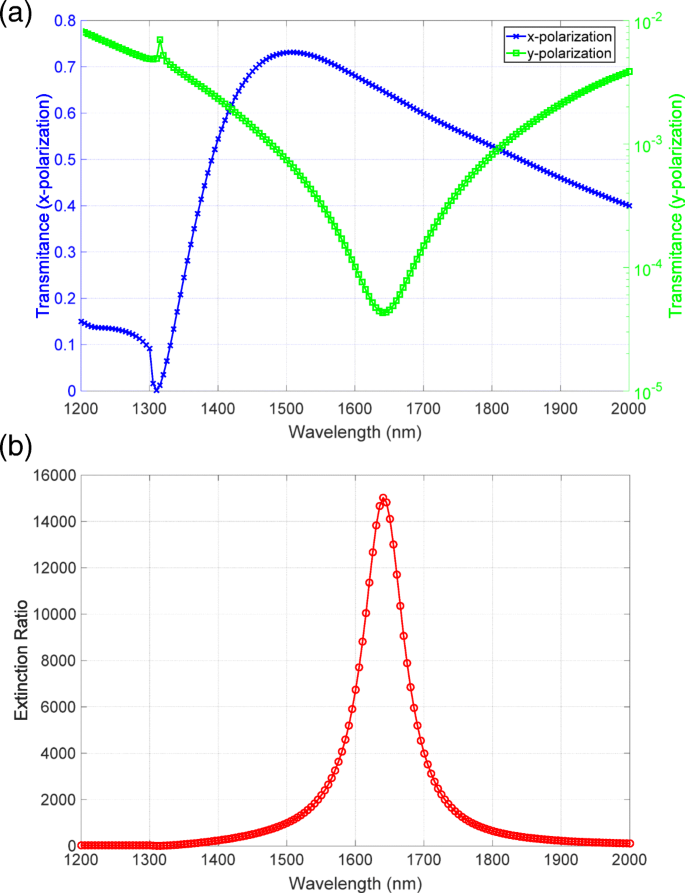
Numerische Berechnungsergebnisse von a Transmission und b Extinktionsverhältnisspektren. Die blauen und grünen Linien in a entsprechen dem x und y Polarisationen bzw.

Nach der experimentellen Demonstration der Metaoberfläche mit dem hohen Extinktionsverhältnis konzentrieren wir uns auf die Stabilität gegenüber zeitlichem Abbau, da die Metaoberfläche Ag enthält, das in der Atmosphäre einem Abbau unterliegt. Abbildung 7 zeigt den zeitlichen Abbau des Extinktionsverhältnisses. Die roten, grünen und blauen Linien sind die Extinktionsverhältnisspektren, die nach 6, 7 bzw. 9 Tagen nach der Metallabscheidung beobachtet wurden. Die rote Linie hat einen Spitzenwert von über 20.000. Nach einem einzigen Tag der Messung der roten Linie verschlechterte sich das Extinktionsverhältnis, hatte aber immer noch einen Spitzenwert von über 10.000. Zwei Tage nach der Messung der grünen Linie verschlechterte sich jedoch das Extinktionsverhältnis signifikant und hatte einen Spitzenwert von 500. Die blaue Linie hat eine verbreiterte Linienbreite, was darauf hindeutet, dass mit dieser Verschlechterung eine Zunahme des Verlustes verbunden wäre. Somit zeigte das Extinktionsverhältnis eine drastische Verschlechterung und die Leistung verschlechterte sich um eine Größenordnung. Wir fanden auch die blauverschobenen Peaks der Extinktionsverhältnisspektren nach dem Abbau. Es wird eine Studie zu einem entscheidenden Faktor beschrieben, der eine Leistungsminderung beinhaltet.

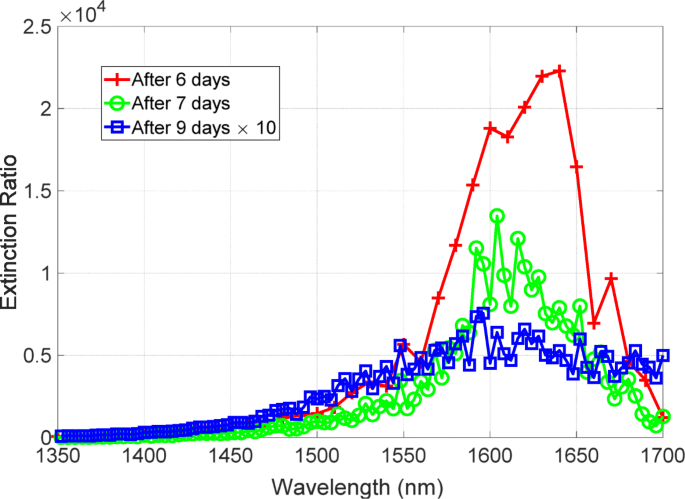
Zeitliche Verschlechterung des Extinktionsverhältnisses. Die roten, grünen und blauen Linien sind die Extinktionsverhältnisspektren für 6, 7 und 9 Tage nach der Metallabscheidung

Der Abbau schritt schnell voran und die Linienbreiten der Extinktionsspektren wurden breiter, was darauf hindeutet, dass einige strukturelle Veränderungen an diesem Abbauprozess beteiligt sind. Daher untersuchen wir, wie sich die Oberflächenmorphologie der metallischen Nanostruktur auf die Leistung des Polarisators auswirkt. Um die Morphologie zu beschreiben, führen wir zwei Modelle ein. Eine beschreibt die Oberfläche durch eine periodische Kurve mit einem Gaußschen weißen Rauschen und die andere durch zufällig verteilte Nanopartikel.

Zunächst untersuchen wir das Modell anhand der periodischen Kurve. Abbildung 8a zeigt die modellierte Oberfläche. Wir haben die Rauheit nur in der unteren Metallschicht eingeführt, um CPU-Zeit und Speicherressourcen zu sparen. Aufgrund der rauen Oberfläche variiert die effektive Dicke der metallischen Schicht. Daher variierten wir die Dicke der unteren Schicht, die durch den grünen Pfeil in Abb. 8b angezeigt wird. Abbildung 9a, b zeigen die Spektren des Transmissions- bzw. Extinktionsverhältnisses dieser Struktur. Selbst in Gegenwart von Rauheit weist der Metaoberflächen-Polarisator hohe Extinktionsverhältnisse in der Größenordnung von 10.000 auf, was anzeigt, dass Rauheit die Leistung nicht wesentlich verschlechtert. Die numerischen Berechnungen haben auch die rotverschobenen Spektren des Extinktionsverhältnisses mit der Abnahme der Dicke gezeigt. Diese Rotverschiebung wird durch die in Fig. 9a gezeigten spektralen Eigenschaften der Durchlässigkeit verdeutlicht. Die hohe Transmission hat eine sehr geringe Empfindlichkeit in Bezug auf die Veränderung der Metalldicke, während die niedrige Transmission die rotverschobene Eintauchposition mit der Abnahme der Dicke hat. Die Peakposition des Extinktionsverhältnisses hängt vom Einbruch der niedrigen Transmission ab, was zur Rotverschiebung führt. Die in der Berechnung aufgetretene Rotverschiebung stimmt nicht mit dem experimentell beobachteten Merkmal der Blauverschiebung überein.

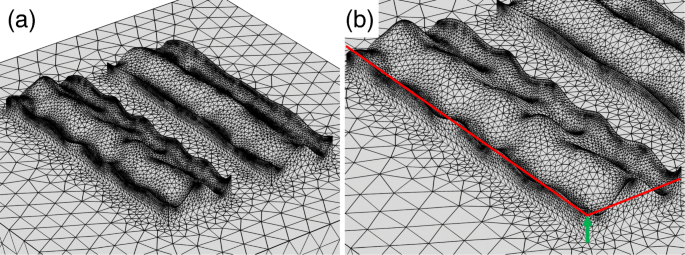
a Aufgeraute Oberfläche, modelliert unter Verwendung einer periodischen Kurve mit einem Gaußschen weißen Rauschen. b Die durch den grünen Pfeil gekennzeichnete Basisdicke wird bei der Berechnung variiert

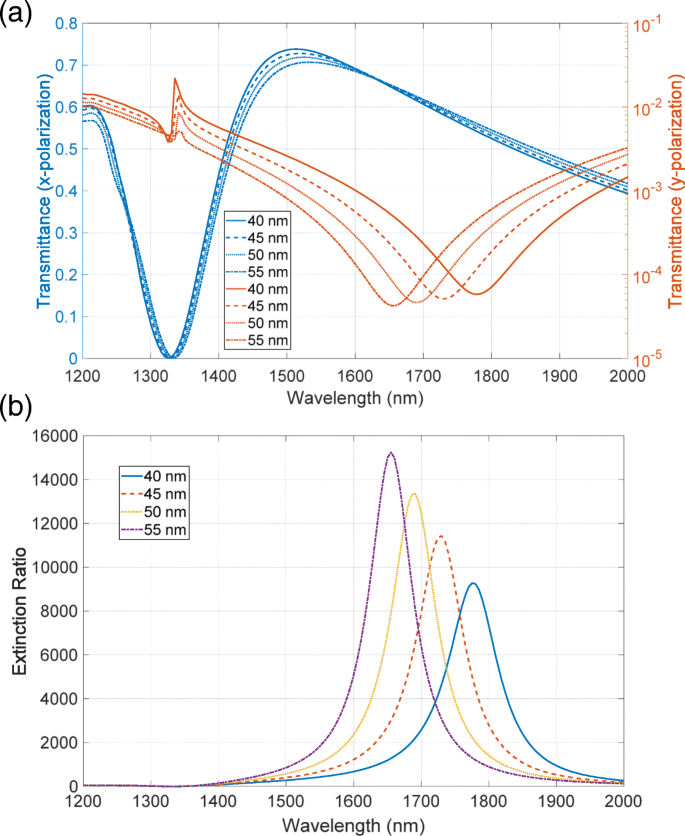
a Transmission und b Extinktionsverhältnisspektren des ersten in Abb. 8 gezeigten Modells. Die Basisdicke der unteren Metallschicht wird von 40 bis 55 nm mit einer Stufe von 5 nm variiert

Zweitens untersuchen wir das Modell anhand der Nanopartikel. Abbildung 10a zeigt die modellierte Oberfläche, bei der Nanopartikel mit Radien von 15, 20 und 25 nm zufällig auf der Oberfläche der unteren Metallstruktur verteilt sind, wie in Abbildung 10b gezeigt. Wir platzierten die halbkugelförmigen Nanopartikel nach gleichmäßig verteilten Zufallszahlen auf der Oberfläche. Unter der zufälligen Verteilung haben einige der Partikel eine leichte räumliche Überlappung und die Maschengröße zwischen den Partikeln wird extrem speicherintensiv. Um Speicher zu sparen, haben wir in diesem Fall eines der Partikel manuell verschoben und die Maschengröße verringert. Die Dicke der unteren Struktur haben wir auf 40 nm eingestellt. Abbildung 11a, b zeigt die Spektren des Transmissions- bzw. Extinktionsverhältnisses dieser Struktur. Ähnlich wie beim ersten Modell hat das Extinktionsverhältnisspektrum einen Spitzenwert in der Größenordnung von 10.000 und verschlechtert sich nicht wesentlich. Der rotverschobene Peak ist auch in Gegenwart der Nanopartikel aufgetreten. Diese Merkmale sind ebenfalls die gleichen wie die im ersten Modell beobachteten, stimmen jedoch nicht mit dem experimentellen Ergebnis der Degradationseigenschaften und der Blauverschiebung überein.

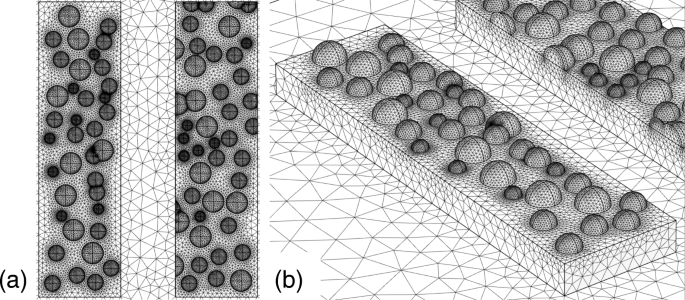
a Die Draufsicht und b Vogelperspektive der rauen Oberfläche, modelliert mit zufällig verteilten Nanopartikeln

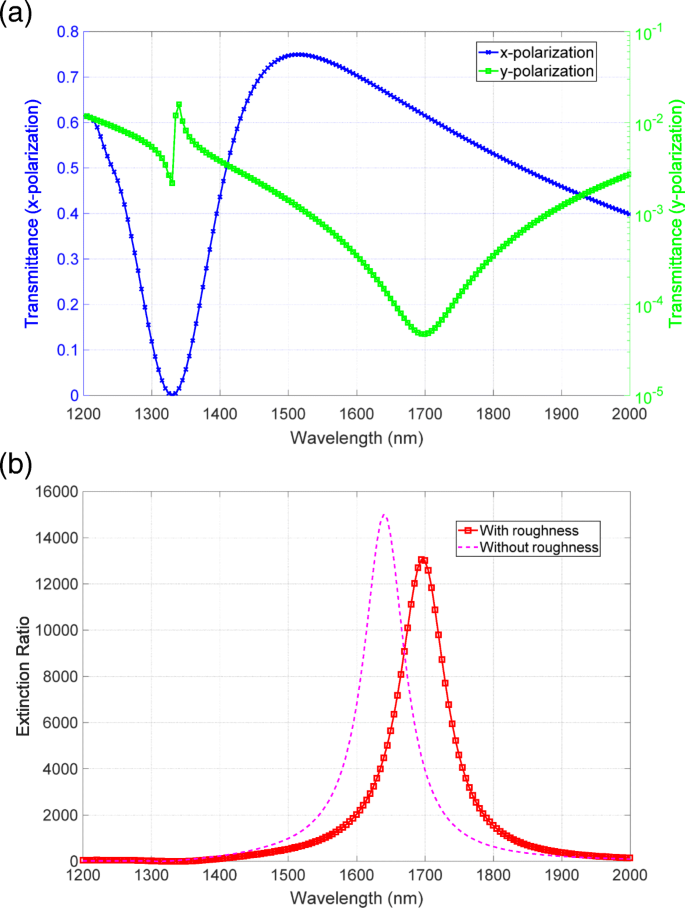
a Transmission und b Extinktionsspektren des zweiten Modells in Abb. 10

In diesem Stadium haben wir numerisch gezeigt, dass die Variation der Oberflächenmorphologie die Leistung des Metaoberflächen-Polarisators nicht signifikant verschlechtert. Diese Robustheit der Morphologie wird dem Babinetschen Prinzip zugeschrieben. Das Babinetsche Prinzip bezieht sich nicht auf die Oberflächenmorphologie, sondern auf die Schirme der komplementären Strukturen. Der auf diesem Prinzip basierende Hochleistungspolarisator wird nicht stark von der Morphologie beeinflusst, da die Schirme selbst bei Vorhandensein der Oberflächenrauhigkeit invariant sind, was zu einer Robustheit gegenüber der Morphologie führt. Daher müssen wir als Ursache des Abbaus einen anderen Effekt der Oberflächenmorphologie berücksichtigen. Hier konzentrieren wir uns auf den metallischen Verlust im Zusammenhang mit der Morphologie. Mit zunehmender Oberflächenrauhigkeit nimmt der Imaginärteil von Ag aufgrund von Oberflächenstreuung und Korngrenzeneffekten zu [36, 37]. Dieser Anstieg des Verlusts wird durch die Dämpfungskonstante des Drude-Modells erklärt, die als γ . beschrieben wird =ρ n e ² /m _e , wobei ρ , n , e , und m _e sind der spezifische elektrische Widerstand, die Elektronendichte, die Elektronenladung und die effektive Elektronenmasse. Der spezifische Widerstand besteht aus zwei Termen. Einer ist der spezifische Volumenwiderstand und der andere ist der Oberflächenwiderstand. Der Oberflächenwiderstand ρ _s ist umgekehrt proportional zur lateralen Korrelationslänge ξ , nämlich ρ _s ξ ⁻¹ [38]. Mit zunehmender Rauheit wird die laterale Korrelationslänge ξ sinkt, was zu einem höheren Oberflächenwiderstand und einem höheren Metallverlust führt. Dieser physikalische Mechanismus wurde nicht in die Berechnung einbezogen, da eine periodische Randbedingung verwendet und eine grobe periodische Struktur angenommen wurde. Wir betrachten die Auswirkungen dieser Erhöhung des Metallverlusts auf das Extinktionsverhältnis und modifizieren die Permittivität von Ag wie folgt:

wo ε _AG ist die Permittivität von Ag aus [32], C eine Konstante ist, die die Zunahme des Metallverlusts darstellt, und i eine imaginäre Einheit bezeichnet. Beachten Sie, dass der Realteil der Permittivität nach der Erhöhung des Imaginärteils geändert werden muss, da Real- und Imaginärteil durch die Kramers-Kronig-Beziehung verbunden sind. In dieser Studie haben wir nur den Imaginärteil modifiziert, um eine qualitative Diskussion zu führen. Unter Verwendung dieser modifizierten Permittivität berechnen wir das Extinktionsverhältnisspektrum. Dieses Ergebnis ist in Abb. 12 dargestellt, in der die Konstante C wird von 1 bis 5 variiert. Das Extinktionsverhältnis nimmt mit steigendem Metallverlust drastisch ab. Außerdem zeigte die Peakposition des Spektrums das blauverschobene Merkmal mit der Zunahme des Verlustes. Diese Merkmale der drastischen Verschlechterung und der Blauverschiebung stimmen gut mit den experimentell beobachteten Merkmalen überein. Der Ursprung dieser Blauverschiebung wird wie folgt aufgeklärt. Der Eintauchwert der niedrigen Transmission wird mit zunehmendem Metallverlust immer flacher. Als Ergebnis nimmt der Beitrag des Spitzenwertes der hohen Transmission zum Extinktionsverhältnis zu. Die Peakposition weist eine starke Unempfindlichkeit gegenüber dem Metallverlust auf und liegt bei der kürzeren Wellenlänge als die Dipposition, was zu einer Blauverschiebung des Extinktionsspektrums führt. Somit haben wir festgestellt, dass die Zunahme des Imaginärteils ein entscheidender Faktor ist, der für die Verschlechterung verantwortlich ist.

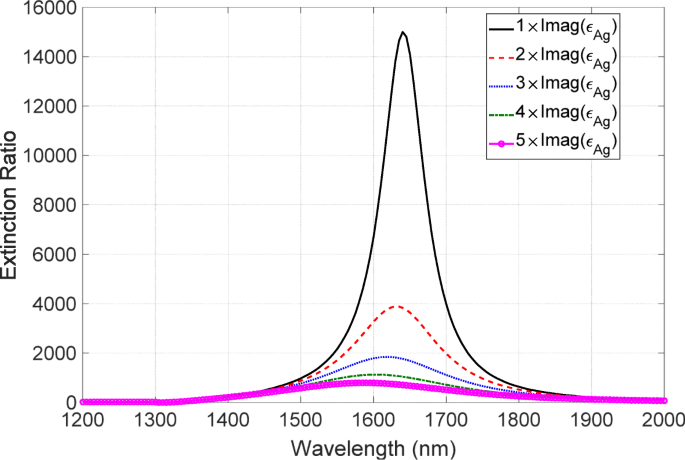
Metallverlustabhängigkeit der Extinktionsspektren. Die schwarzen, roten, blauen, grünen und magentafarbenen Linien entsprechen den Fällen von C =1,2,3,4 bzw. 5

Wir schlagen vor, dass das Extinktionsverhältnis durch Variation der Dicken der komplementären Metallschichten erhöht wird. Die Spitzenposition der hohen Durchlässigkeit liegt bei einer kürzeren Wellenlänge als die Neigungsposition der niedrigen Durchlässigkeit. Um das Extinktionsverhältnis zu verbessern, sollten diese Peak- und Dip-Positionen nahe beieinander liegen. Nach dem Babinet-Prinzip müssen Peak und Dip die gleiche Wellenlänge haben. Das Prinzip geht jedoch davon aus, dass komplementäre Strukturen einen perfekten elektrischen Leiter mit einer unendlich dünnen Dicke aufweisen, was im optischen Bereich selbst unter Näherung schwer zu validieren ist. Dadurch haben die komplementären Strukturen unterschiedliche Resonanzwellenlängen. Um die Wellenlängen einzustellen, betrachten wir die Eigenschaften der Eigenmoden, die für die Resonanzen verantwortlich sind. Fig. 13a, b zeigen die Verteilungsmuster des elektrischen und magnetischen Felds an den Spitzen- bzw. Einbruchstellen der in Fig. 6 gezeigten Durchlässigkeit. Diese Feldverteilungen sind im z . dargestellt −x Flugzeug um y =0 bei einer einfallenden Lichtintensität von 1 W. Die Eigenmode der hohen Transmission hat die Eigenschaft eines elektrischen Dipols in der oberen Metallstruktur, während die der niedrigen Transmission die Eigenschaft einer magnetischen Schleife in der unteren Struktur hat. Die Resonanzwellenlänge für die hohe Transmission wird durch die Breite des Luftlochs im z . bestimmt −x Flugzeug. Dies ist ein fester Parameter und kann nicht angepasst werden. Andererseits wird die Resonanzwellenlänge für die niedrige Transmission durch den Querschnitt der Bodenstruktur im z . bestimmt −x Flugzeug. Dies ist durch Variation der Metallstärke einstellbar. Diese Einstellungen stimmen mit der Dickenabhängigkeit der Durchlässigkeit überein, dass die Spitzenposition der hohen Durchlässigkeit eine geringe Empfindlichkeit gegenüber der Dicke der unteren Metallschicht aufweist, während die Eintauchposition der niedrigen Durchlässigkeit eine hohe Empfindlichkeit aufweist. Basierend auf dieser Analyse stellen wir die Wellenlänge wie folgt ein. Mit zunehmender Dicke nimmt der Querschnitt zu und die Resonanzwellenlänge der niedrigen Transmission verschiebt sich zu kürzeren Wellenlängen. Als Ergebnis nähern sich die Spitzen- und Einbruchpositionen und das Extinktionsverhältnis wird verbessert. Um dies zu bestätigen, berechnen wir die Abhängigkeit der Transmissions- und Extinktionsverhältnisspektren von der Dicke. In dieser Berechnung haben wir die Dicke der oberen Metallschicht auf 45 nm festgelegt. Abbildung 14a zeigt die Transmissionsspektren für das x und y Polarisationen. Mit der Zunahme der Dicke verschiebt sich die Neigungsposition der niedrigen Durchlässigkeit zu kürzeren Wellenlängen und die Neigung wird tiefer. Andererseits wird die Spitzenposition der hohen Durchlässigkeit durch das Variieren der Dicke nicht stark beeinflusst, selbst wenn der Spitzenwert um 5 % abnimmt. Abbildung 14b zeigt die Extinktionsverhältnisspektren. Wenn die Dicke 35 oder 40 nm beträgt, wird der Abfall der niedrigen Durchlässigkeit flacher als der von 45 nm, was zu einem niedrigeren Extinktionsverhältnis führt. Wenn die Dicke 50 oder 55 nm beträgt, gibt es fast keine Verstärkung. Dies liegt daran, dass die Verbesserung durch die Einstellung der Spitzen- und Einbruchspositionen durch die Abnahme des Spitzenwertes der hohen Durchlässigkeit aufgehoben wird. Wenn die Dicke 60 oder 65 nm beträgt, gibt es eine deutliche Verbesserung des Extinktionsverhältnisses. Dies liegt an der Kombination des tieferen Dip-Wertes und der Verbesserung durch die Positionsanpassung. Wie wir numerisch gezeigt haben, kann eine weitere Verbesserung des Extinktionsverhältnisses durch Anpassen der Dicken der komplementären Metallstrukturen realisiert werden. Solche variierenden Dicken könnten durch wiederholte Metallabscheidung realisiert werden. Zuerst Metallabscheidung mit einer Dicke von a wird auf einem strukturierten Substrat durchgeführt. Anschließend wird durch Abwischen mit einem sauberen Tuch nur die oberste Metallschicht mit einer Metalldicke von a . von der Oberfläche des Substrats entfernt . Anschließend Metallabscheidung mit einer Dicke von b wird an der Probe durchgeführt. Als Ergebnis werden die Dicken der oberen und unteren Schichten b und a +b , bzw.

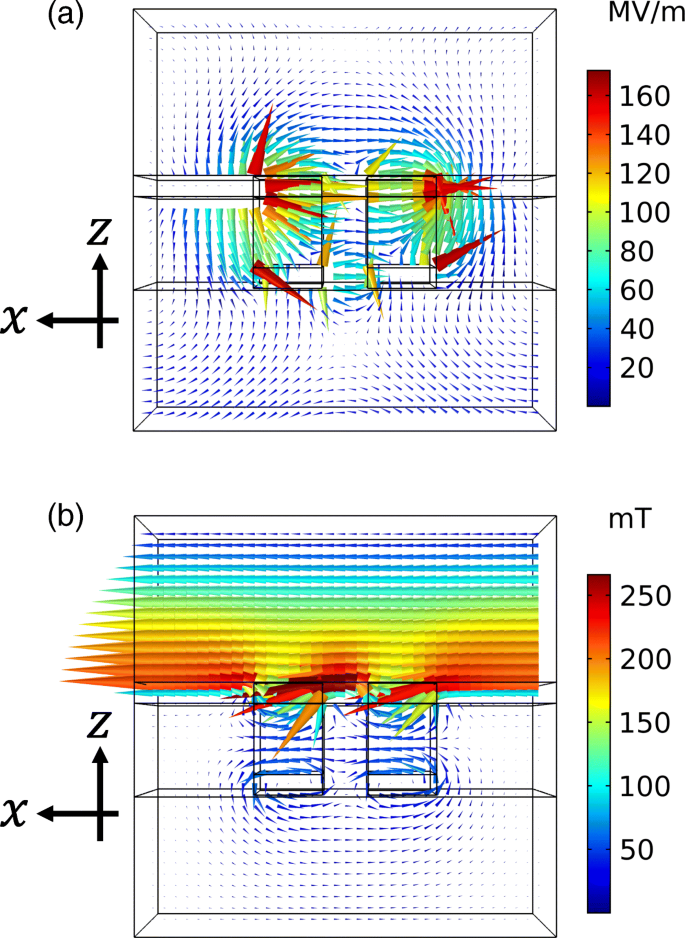
a Verteilungsmuster des elektrischen Felds an der Spitze der hohen Durchlässigkeit, wie in Abb. 6 gezeigt. b Verteilungsmuster des magnetischen Feldes an der Senke des niedrigen Transmissionsgrades, gezeigt in Abb. 6. Die Pseudofarbe zeigt die Intensität des Vektorfeldes an

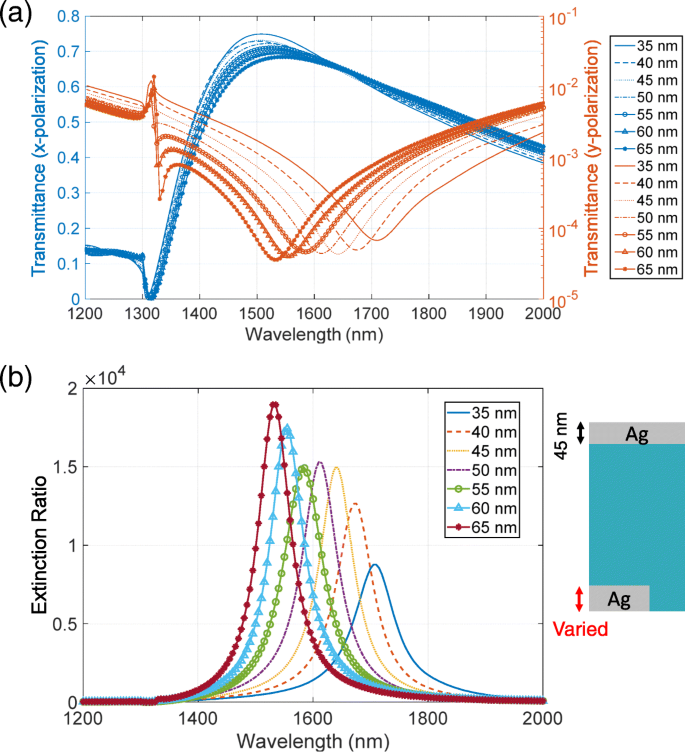
a Transmission und b Extinktionsverhältnisspektren, wenn die komplementären Metallschichten unterschiedliche Dicken aufweisen. Die Dicke der oberen Metallschicht ist auf 45 nm festgelegt, während die Dicke der unteren Schicht von 35 bis 65 nm in Schritten von 5 nm variiert wird (siehe Einschub in b )

Schlussfolgerungen

Wir haben die Degradationseigenschaften des Hochleistungs-Metasurface-Polarisators untersucht. Die präparierte Metaoberfläche zeigte ein hohes Extinktionsverhältnis in der Größenordnung von 10.000. Wir haben festgestellt, dass die hohe Leistung allmählich nachgelassen hat. Um den Ursprung dieser Degradation zu klären, haben wir die Auswirkungen der Oberflächenmorphologie auf das Extinktionsverhältnis untersucht. Zur Beschreibung der Oberflächenmorphologie wurden zwei Modelle vorgestellt. Einer modelliert eine raue Oberfläche durch eine Kombination aus einer periodischen Kurve und einem Gaußschen weißen Rauschen, während der andere die Oberfläche durch zufällig verteilte Nanopartikel modelliert. Beide Modelle zeigten, dass sich die hohe Leistung nicht durch die Oberflächenrauheit verschlechterte. Dies liegt daran, dass das hohe Extinktionsverhältnis durch das Babinet-Prinzip bestimmt wird, was zur Robustheit der Oberflächenmorphologie führt. We have also investigated the relation between the extinction ratio and the increase in metallic loss because of the surface roughness, which showed drastic degradation of the extinction ratio. The spectral feature of the blue-shift was also reproduced by the numerical calculation, indicating that the degradation is due to the increase in the metallic loss. From this result, we find that the metal deposition should be conducted to reduce the scattering and grain boundary losses that are related to the roughness. Throughout the numerical calculation, we have found that the low transmittance has a high sensitivity to the surface morphology, while the high transmittance does not have the high sensitivity. By utilizing these findings, we proposed that the extinction ratio can be enhanced by varying the thicknesses of the metallic layers. This study paves a way for the development of a metasurface with a high performance and stability toward time degradation.

Abkürzungen

BS:

Beam sampler

GLP:

Glan-laser prism

NDF:

Neural density filter

OPO:

Optical parametric oscillator

PhC:

Photonic crystal

SEM:

Rasterelektronenmikroskop

YAG:

Yttrium iron garnet