Spin und Orbitalrotation von plasmonischem Dimer, angetrieben durch zirkular polarisiertes Licht

Hintergrund

Die optische Bindung zweier Mikropartikel (MPs) oder Nanopartikel (NPs), die mit einem linear polarisierten (LP) Licht bestrahlt werden, ist ein wichtiges optomechanisches Verhalten, das das Ergebnis der Licht-Materie-Wechselwirkung ist [1,2,3,4]. Zwischen dem optisch gebundenen Dimer gibt es mehrere stabile Gleichgewichts-Interpartikel-Abstände; diese Abstände sind fast ganzzahlige Vielfache der Wellenlänge im Medium [3,4,5,6]. Außerdem ist die Orientierung des Dimers senkrecht zur Polarisation des LP-Lichts. Da der Abstand zwischen den Partikeln nahe bei ganzzahligen Vielfachen der Wellenlänge liegt, erzeugen die gestreuten Photonen zwischen den Partikeln eine konstruktive Interferenz, um eine Bindungskraft zu induzieren. Die Phänomene der optisch gebundenen Anordnung mehrerer Siliziumdioxid-MPs oder Ag-NPs wurden ebenfalls untersucht [7,8,9,10]. Für die Beleuchtung einer zirkular polarisierten (CP) ebenen Welle haben Haefner et al. berichteten, dass die Helizitäten des longitudinalen Spins und der Orbitalrotation der beiden gekoppelten Silica-NP mit einer Größe von 100–700 nm mit der Händigkeit des einfallenden Lichts identisch sind [11]. Vor kurzem haben Sule et al. experimentell festgestellt, dass die Helizität der Orbitalrotation zweier Ag-NPs mit einem Radius von 75 nm, die durch eine optische Kraft gebunden sind, der Händigkeit eines fokussierten CP-Gaußschen Strahls von 790 nm in Wasser entgegengesetzt ist [12]; d. h. Ag-Dimer erleidet ein negatives optisches Orbitaldrehmoment [13, 14]. Außerdem betrug die gemessene Umlaufbahnrotation etwa 4 kHz [12]. Andererseits wurde auch der Spin eines einzelnen Au-NP mit einem Radius von 100 nm, der durch einen CP-Gaußschen Strahl induziert wird, untersucht [15,16,17,18]. Die gemessene Spinrotation betrug 3,5 kHz [15]. In den letzten Jahrzehnten hat die longitudinale/transverse Spin-Bahn-Kopplung (SOC) des optischen Feldes viel Aufmerksamkeit auf sich gezogen [19,20,21,22,23]. Beispielsweise kann ein optischer Wirbelstrahl (z. B. Laguerre-Gauss-Strahlen höherer Ordnung mit azimutaler oder radialer Polarisation) oder ein hochfokussierter CP-Gaußscher Strahl verwendet werden, um den SOC zu induzieren [24,25,26,27,28,29,30 ,31,32,33,34]. Das verdrillte elektromagnetische (EM) Feld des optischen Wirbelstrahls trägt sowohl den Spindrehimpuls als auch den Bahndrehimpuls und induziert dadurch den longitudinalen/transversalen Spin und die Bahnrotation eines nahegelegenen Sondierungs-NP [18,19,20,21,22,23 ,24,25,26]. Insbesondere der SOC im Nahfeld von Au- oder Ag-NPs ist aufgrund der kollektiven Bewegung freier Elektronen in diesen NPs (Plasmoneneffekt) signifikanter [28,29,30,31].

In diesem Artikel untersuchen wir theoretisch das optomechanische Verhalten (optische Kräfte und Drehmomente) zweier gekoppelter Au-NPs (Dimer), die von einem Substrat getragen werden und durch die Beleuchtung eines CP-Gaußschen Strahls induziert werden. Das Substrat ist notwendig, um diese freistehenden NPs einzugrenzen, die sich in der Fokusebene bewegen, anstatt im 3D-Raum zu schweben. Die Multiple Multipole (MMP)-Methode wird verwendet, um das EM-Feld numerisch zu simulieren und dann die optischen Orbital- und Spin-Drehmomente auf dem optisch gebundenen Dimer zu analysieren [35, 36]. Durch die optomechanischen Reaktionen des Dimers wird der Längs-/Quer-SOC manifestiert. Insbesondere wird auch die Bedingung untersucht, ein negatives optisches Orbitaldrehmoment am Dimer zu erzeugen.

Methoden

Abbildung 1 zeigt die Konfiguration eines Paares identischer Au-NPs, die von einem Substrat getragen und mit einem normal einfallenden linkshändigen (LH) CP-Licht (ebene Welle oder Gaußscher Strahl) bestrahlt werden, wobei d repräsentiert den Partikelabstand. Die Taille des Gaußschen Strahls wird mit w . bezeichnet ₀ , und die Brennebene befindet sich im zentralen Querschnitt der Au-NPs. Die Formulierungen des elektrischen Feldes der ebenen Welle und des Gaußschen Strahls sind als Anhang beigefügt. Wir nehmen an, dass der Brechungsindex des Substrats gleich dem des umgebenden Mediums Wasser ist. Daher wird das reflektierte Licht nicht an der Grenzfläche zwischen dem Medium und dem Substrat induziert; das optische Feld wird durch das Vorhandensein des Substrats nicht gestört [37]. Andererseits dient die Existenz des Substrats als Einschränkung, um die NPs zu unterstützen, die sich auf dem Substrat bewegen. Zur Simulation des induzierten elektromagnetischen Feldes wird das Multiple Multipol (MMP)-Verfahren verwendet [17, 18, 35, 36]. Die optischen Kräfte F ^j ausgeübt auf die j NP (j = 1, 2) werden ausgedrückt durch

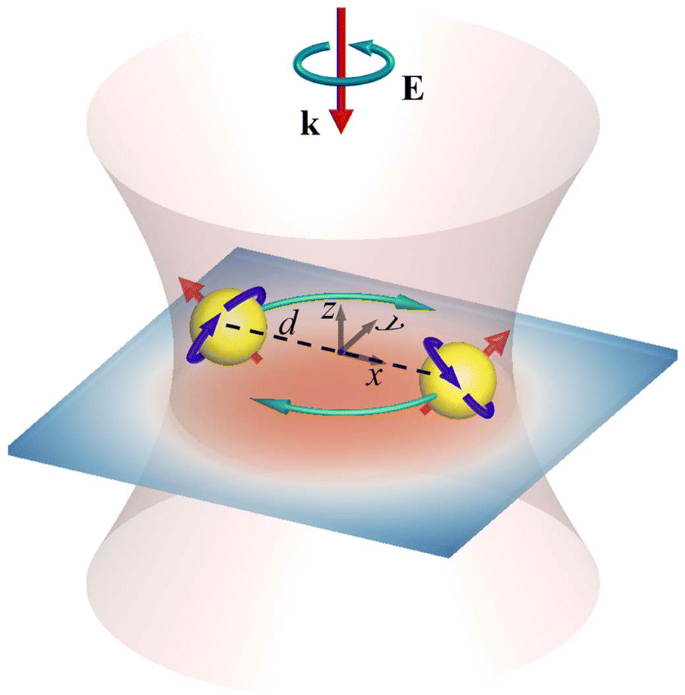
Konfiguration eines NP-Paares mit einem tragenden Substrat, bestrahlt mit einem normal einfallenden LH-CP-Gaußschen Strahl der Taille (w0). Die zentralen Querschnitte dieser NPs befinden sich in der Brennebene des Gaußschen Strahls, und d ist der Abstand zwischen den Zentren der NPs. Die optomechanischen Reaktionen sind die longitudinale Orbitalrotation und der longitudinale/quere Spin

Hier, n ist der nach außen gerichtete Normalenvektor auf der Oberfläche des j NP und T ist der zeitlich gemittelte Maxwell-Spannungstensor, ausgedrückt als

In Gl. (2), ich eine 3 × 3-Identitätsmatrix ist, bezeichnet der Überstrich die komplex Konjugierte und Re den Realteil [17, 18, 35, 36]. Hier, ε und μ sind die Permittivität und Permeabilität des umgebenden Mediums. Beachten Sie, dass das E und H sind das äußere Gesamtfeld, das für Gl. (2). Tatsächlich T ist auch der zeitlich gemittelte lineare Impulsfluss. In diesem Artikel werden die optischen Kräfte in den Zylinderkoordinaten ausgedrückt:radial, azimutal und z -Achsenkomponenten. Die Radialkraft kann die Anziehung oder Abstoßung zwischen den beiden NPs und die Azimutalkraft die Helizität der Umlaufbahn der NPs erklären.

Andererseits ist das optische Spin-Torque auf dem j NP (j = 1, 2) für das Spinnen einzelner NP ist gegeben durch,

In Gl. (3), x ^j × T ist der Drehimpulsfluss und x ^j ist der relative Positionsvektor eines Punktes x an der Oberfläche S _j bezogen auf den Massenschwerpunkt \({\mathbf{x}}_c^j\)von j NP; \( {\mathbf{x}}^j=\mathbf{x}-{\mathbf{x}}_c^j\). Die Längsrichtung wird als parallel zur optischen Achse bezeichnet (sagen wir z Richtung) des einfallenden Lichts und die Querrichtung ist senkrecht zur optischen Achse. Andererseits ist das longitudinale optische Orbitaldrehmoment im z Richtung auf jedem NP, verursacht durch die azimutale optische Kraft, ist definiert als F _θ d /2 in den Zylinderkoordinaten. Die relative Permittivität von Au bei λ = 800 nm, das in der Simulation verwendet wird, ist (− 24,062, 1,507) [38].

Ergebnisse und Diskussion

Wir untersuchen die optischen Kräfte und Drehmomente, die auf zwei identische Au-NPs mit Radien von 100 nm ausgeübt werden, die von einer normal einfallenden ebenen LH-CP-Welle oder einem fokussierten Gaußschen Strahl in der Brennebene bestrahlt werden. Das umgebende Medium ist Wasser. Die Fluenz der ebenen Welle oder des Gaußschen Strahls in der Mitte beträgt 25 MW/cm ² . Die Zentren der beiden freistehenden NPs, unterstützt von einem virtuellen Substrat, können sich in der xy . bewegen Ebene (Fokusebene). Die optischen Kräfte (F _r , F _θ ) gegen den Partikelabstand d für eine ebene CP-Welle oder einen fokussierten Gaußschen Strahl mit einer Taille von 500 nm von λ = 800 nm sind in Fig. 2a bzw. b gezeigt. Der zentrale Querschnitt dieser NPs liegt in der Brennebene des Gaußschen Strahls. Abbildung 2a zeigt, dass es für eine ebene Welle mehrere Teilchenabstände im stabilen Gleichgewicht mit F . gibt _r = 0 und eine negative Steigung; der erste d ₁ liegt bei 603 nm und der zweite d ₂ bei 1204 nm. Diese Abstände zwischen den Teilchen im „stabilen Gleichgewicht“ sind fast die ganzzahligen Vielfachen der Wellenlänge im Medium; d.h. d _m =mλ /n , wobei n ist der Brechungsindex des Mediums und m = 1, 2, 3... Dies ist das Ergebnis der weitreichenden Licht-Materie-Wechselwirkung, die durch die optische Bindungskraft verursacht wird. Es deutet darauf hin, dass es eine optische Feder gibt, die die beiden NPs verbindet; die Rückstellkraft F _r der optischen Feder hält die NPs bei diesen stabilen Gleichgewichts-Zwischenteilchen-Abständen voneinander entfernt. Im Fall des Gaußschen Strahls sind die ersten beiden stabilen Gleichgewichts-Zwischenteilchen-Abstände d ₁ und d ₂ sind 585 bzw. 1131 nm, wie in Abb. 2b gezeigt, etwas kleiner als die einer ebenen Welle aufgrund der durch den Gaußschen Strahl induzierten Gradientenkraft.

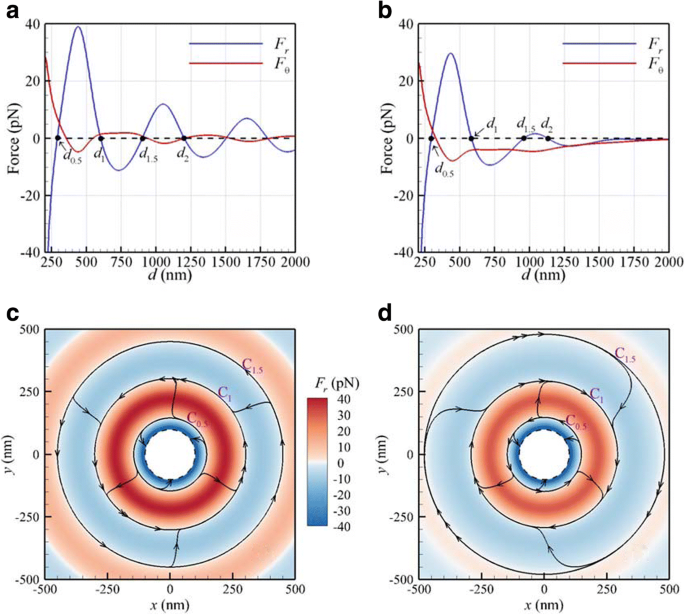
Optische Kräfte (F _r , F _θ ) gegen d für λ = 800 nm von CP a ebene Welle und b Gaußscher Strahl mit einer Taille von 500 nm in der Brennebene. Die 2D-Stromlinienkarten der optischen Kraft (F _r , F _θ ) durch CP induziert c ebene Welle und d Gaußscher Strahl. Der Farbbalken repräsentiert die Amplitude von F _r . Der gestrichelte Ring ist der Grenzkreis der Mittelpunkte zweier NPs, an denen sich die NPs berühren

Tatsächlich ist das longitudinale Orbitaldrehmoment F _θ d /2 wird diese NPs dazu bringen, sich in Umlaufbahnen mit Durchmessern von d . zu drehen ₁ und d ₂ . In den Fällen mit dem Gaußschen Strahl werden die Umlaufbahnen an der Strahlachse zentriert. Das Vorzeichen der azimutalen optischen Kraft (F _θ ). Dies zeigt, dass das negative F _θ des CP-Gaußschen Strahls erzeugt ein negatives Orbitaldrehmoment F _θ d ₁ /2 auf der ersten stabilen Gleichgewichtsbahn; noch wichtiger ist, dass die Helizität der Orbitalrotation des Au-Dimers der Händigkeit des einfallenden CP-Lichts entgegengesetzt ist [12]. Es ist auch von Interesse zu beachten, dass F _θ ist immer negativ als d> 300 nm für die Fälle mit dem Gaußschen Strahl; das Phänomen der umgekehrten Rotation (Umdrehung) der optisch gebundenen NPs aufgrund eines negativen Orbitaldrehmoments kann in optischen Pinzettensystemen leicht beobachtet werden. Das negative optische Orbitaldrehmoment könnte auf das verdrehte EM-Feld des Gaußschen Strahls zurückgeführt werden [23].

Nach dem Stokes’schen Gesetz einer von einer Kraft angetriebenen Kugel F um sich in einer viskosen Flüssigkeit zu bewegen, die Endgeschwindigkeit v _T ist v _T = F /(6πrη ), wobei η ist die dynamische Viskosität von Wasser (0,001 kg/m s). Dies ist das Ergebnis der aufgebrachten Kraft, die durch eine Widerstandskraft einer viskosen Flüssigkeit ausgeglichen wird [39]. Nach dem Stokes-Gesetz ist der Endgeschwindigkeitsvektor einer NP in einem viskosen Medium proportional zur aufgebrachten Kraft [39]. Daher haben wir das optische Kraftfeld verwendet, um die Stromlinien zu erhalten, die den Bahnen dieser NPs fast äquivalent sind. Darüber hinaus können die 2D-Stromlinienkarten direkt aus dem optischen Kraftvektorfeld (F _r , F _θ ), die auf NPs ausgeübt werden, sind in Abb. 2c, d für eine ebene Welle bzw. einen Gaußschen Strahl aufgetragen, wobei der Farbbalken die Amplitude von F . darstellt _r . Beachten Sie, dass die Tangente der Stromlinie an jedem Punkt dann parallel zum optischen Kraftvektor und damit auch parallel zur Geschwindigkeit von NP ist. Für kleinen Partikelabstandsbereich (d < d _0.5 ), die radiale optische Kraft F _r negativ ist, ziehen sich diese beiden NPs gegenseitig an, um schließlich zu kollidieren, wie in Abb. 2c, d gezeigt. Der gestrichelte Ring ist der Grenzkreis der Mittelpunkte zweier NPs, an denen sich die NPs berühren. Der innere Ring (blau) ist ein Bereich der Nahbereichswechselwirkung. Der innere Ring C _0.5 zwischen dem inneren Ring (blau, mit negativem F _r ) und der zweite Ring (rot, mit positivem F _r ) ist die Grenzlinie zwischen den Nah- und Fernwechselwirkungsregionen des Au-Dimers; der Durchmesser von C _0.5 ist d _0.5 = 291 nm in Abb. 2c und d _0.5 = 296 nm in Abb. 2d. Auf lange Sicht (d _0.5 < d < d _1.5 ) treiben die radialen und azimutalen optischen Kräfte die beiden gekoppelten NPs an, sich der ersten stabilen Gleichgewichtsbahn C . zu nähern ₁ mit einem Durchmesser d ₁ aufgrund der Wirkung der optischen Bindungskraft. Das optisch gebundene Au-Dimer rotiert gegen den Uhrzeigersinn (CCW) entlang der Umlaufbahn C ₁ (d ₁ = 603 nm) in Abb. 2c, während entlang C ₁ (d ₁ = 585 nm) im Uhrzeigersinn (CW) in Abb. 2d. Die erstgenannte Rotation entspricht der Händigkeit des einfallenden Lichts, die durch das positive Umlaufdrehmoment (F _θ > 0), und letztere ist wegen des negativen Umlaufdrehmoments (F _θ < 0). Gemäß unserer Analyse des Streuquerschnittsspektrums eines Dimers mit einem stabilen Gleichgewichtsabstand von 603 nm, das von einer ebenen CP-Welle (hier nicht gezeigt) bestrahlt wird, liegt die Kopplungsoberflächenplasmonenresonanz (SPR) des optisch gebundenen Dimers fast bei 800 nm entsprechend dem einfallenden Licht, das eine Off-Resonanz eines einzelnen NP ist (530 nm). Im Allgemeinen hängt die Kopplungs-SPR eines Dimers vom Partikelabstand ab; je größer der Abstand, desto rotverschobener ist die Kopplungs-SPR des Dimers. Wenn wir einen Gaußschen Strahl mit längerer Wellenlänge verwenden (z. B. 1064 nm), erhöht sich der Abstand zwischen den Teilchen im stabilen Gleichgewicht. Wenn jedoch der Abstand zwischen den beiden NPs zu groß wird, nimmt der optische Kopplungseffekt ab, so dass die Kopplungs-SPR allmählich verschwindet. Folglich wird die SPR eines einzelnen NP bei 530 nm dominant.

Für einen Au-NP mit einem Radius von 100 nm, der sich auf einer Umlaufbahn mit einem Durchmesser von d . bewegt und eine Winkelgeschwindigkeit Ω_z , die Geschwindigkeit beträgt Ω_z d /2 = F _θ /(6πrμ ). Wenn der Gaußsche Strahl angewendet wird (F _θ = − 4 pN), die Winkelgeschwindigkeit Ω_z (Zyklen pro Sekunde) entlang C ₁ beträgt etwa − 7 kHz. Die Größenordnung stimmt mit dem experimentellen Ergebnis überein [12]; die Winkelgeschwindigkeit der Orbitalrotation zweier Ag-NPs von r = 75 nm, die vom Gaußschen Strahl mit 14 mW bestrahlt wird, ist − 4 kHz. Wenn d _1.5 < d < d _2.5 , werden sich diese NPs der sekundären stabilen Gleichgewichtsbahn C . nähern und entlang dieser rotieren ₂ (hier nicht abgebildet). Beachten Sie, dass für diese Fälle die optische Kraft von F _z ist negativ, um diese NPs aufgrund des Strahlungsdrucks stromabwärts zu drücken; F _z = − 161.3 pN für die ebene Welle und − 117,2 pN für den Gaußschen Strahl. Daraus folgt, dass die Reaktionskraft des tragenden Substrats notwendig ist, um die treibende optische Kraft von F . auszugleichen _z . Folglich sind die resultierenden Kräfte in z Richtung auf diesen NPs sind null; diese beiden NPs sind darauf beschränkt, sich in der xy zu bewegen Ebene der Fokusebene.

Andererseits zeigen Abb. 3a, b die optischen Spindrehmomente (M _r , M _θ , M _z ) gegen d induziert durch eine ebene Welle bzw. einen Gaußschen Strahl in der Brennebene. Da die Ergebnisse dieser beiden NPs gleich sind, ist hier nur ein Satz optischer Spindrehmomente aufgetragen. Die ersten beiden (M _r , M _θ ) sind die transversalen Spindrehmomente, und letztere M _z ist der Längsschnitt. Es hat sich herausgestellt, dass die Helizität des longitudinalen Spin-Drehmoments in beiden Fällen gleich der Händigkeit des einfallenden Lichts ist. Dies liegt daran, dass der Drehimpuls absorbierter Photonen des einfallenden CP-Lichts auf diese NPs zum Drehen und Orbitalrotieren übertragen wird. Es ist von Interesse, darauf hinzuweisen, dass die transversalen optischen Spindrehmomente (M _r , M _θ ), die durch einen Gaußschen Strahl induziert werden, sind im Vergleich zu denen durch die ebene Welle signifikant groß. Dies könnte auf die transversalen Komponenten des verdrillten EM-Feldes in der Brennebene eines Gaußschen Strahls zurückgeführt werden. Darüber hinaus treten die maximalen Beträge der optischen transversalen Spindrehmomente ungefähr auf der ersten stabilen Gleichgewichtsbahn C . auf ₁ (d ₁ = 585 nm), wie in Abb. 3b gezeigt. Nach dem Stokes-Gesetz einer rotierenden Kugel, die durch ein Drehmoment M . gedreht wird in einer viskosen Flüssigkeit beträgt die Endwinkelgeschwindigkeit der Kugel ω _T = M /(8πr ³ μ ) [18]. Daher sind die Größen der longitudinalen/transversalen Spinwinkelgeschwindigkeiten von NP bei C ₁ sind etwa 10 kHz, von denen die Größenordnungen mit der gemessenen longitudinalen Spingeschwindigkeit [15], etwa 3,5 kHz, übereinstimmen. Zusammenfassend können die obigen Phänomene, wie in den Fign. 2b und 3b zeigen, dass die longitudinale Orbitalrotation von den longitudinalen/transversalen Spins begleitet wird. Die Bewegung der beiden gekoppelten NPs ähnelt der eines Doppelsternsystems, in dem die optischen Kräfte die Bindungs- und Bahnantriebskräfte für diese NPs bereitstellen sowie die optischen Spindrehmomente ihre Drehung verursachen.

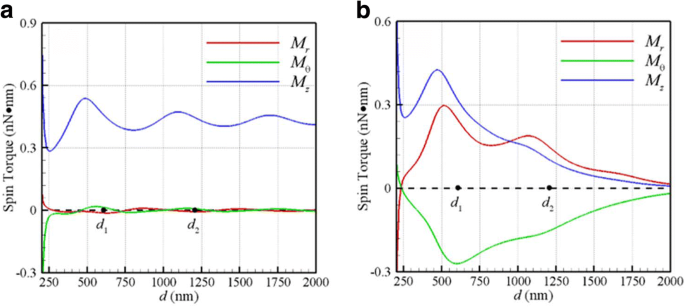
Optische Spin-Drehmomente (M _r , M _θ , M _z ) gegen d bei λ = 800 nm für a ebene Welle und b Gaußscher Strahl mit w ₀ = 500 nm in der Brennebene

Außerdem kann man die Iris des Objekts einer optischen Pinzette einstellen, um die Größe des einfallenden Strahls zu ändern, wodurch die numerische Apertur und die Taille eines Gaußschen Strahls geändert werden. Abbildung 4a zeigt das optische Orbitaldrehmoment F _θ d /2 auf zwei gekoppelten Au-NPs mit einem Radius von 100 nm, die auf der entsprechenden ersten Umlaufbahn im stabilen Gleichgewicht (d = d ₁ ) gegenüber der Taille eines CP-Gaußschen Strahls von λ = 800 nm. Der entsprechende erste stabile Gleichgewichtsabstand d ₁ ist auch in Abb. 4a aufgetragen (Skalenbalken rechts), wo eine ebene Welle als Spezialfall von w . behandelt werden kann ₀ → ∞. Der Wendepunkt für die Taille eines Gaußschen Strahls zwischen dem positiven und dem negativen Orbitaldrehmoment liegt bei 1150 nm, entsprechend F _θ = 0, wie in Fig. 4a gezeigt. Je kleiner die Taille eines Gaußschen Strahls ist, desto größer ist der Betrag des negativen Umlaufdrehmoments. Wenn die Taille zunimmt, wird das d ₁ eines Gaußschen Strahls nähert sich dem Wert (603 nm) einer ebenen Welle (w ₀ → ∞). Insbesondere wenn die Taille abnimmt, werden die Größen der Querspin-Drehmomente (M _r , M _θ ) um d ₁ deutlich ansteigen, während das Längsdrehmoment M _z abnimmt, wie in Abb. 4b gezeigt. Diese Ergebnisse veranschaulichen, dass die Taille eines Gaußschen Strahls der Schlüsselfaktor ist, um ein negatives longitudinales Orbitaldrehmoment und transversale Spindrehmomente aufgrund des Grades der Verzerrung des EM-Felds zu induzieren.

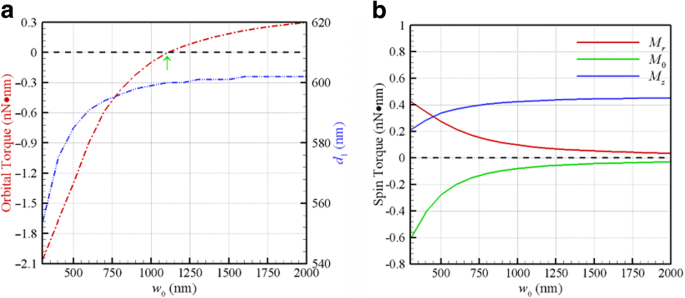
a Das optische Orbitaldrehmoment und d ₁ auf der ersten stabilen Gleichgewichtsbahn gegenüber der Taille eines Gaußschen Strahls von λ = 800 nm. Der Wendepunkt der Taille zur Erzeugung eines positiven oder negativen Umlaufdrehmoments liegt bei 1150 nm. b Die optischen Spin-Torques im Vergleich zur Taille bei d ₁

Der Mechanismus der negativen Orbitalrotation und des transversalen Spinnens dieser NPs könnte auch ohne den Beitrag des Bahndrehimpulses des Lichtstrahls auf die Drehung des Spindrehimpulses des Lichtfelds zurückgeführt werden [23]. Durch das Verhalten des negativen longitudinalen Orbitaldrehmoments und des transversalen Spindrehmoments auf Au-Dimer kann der plasmonenverstärkte SOC von Photonen manifestiert werden. Darüber hinaus hängen die Richtungen der Orbitalrotation des Dimers und der Spin einzelner NP von der Händigkeit des einfallenden Lichts ab.

Schlussfolgerungen

Die optomechanischen Reaktionen (optische Kräfte und Drehmomente) eines Paares von Au-NPs, die mit CP-Licht bestrahlt wurden, wurden theoretisch untersucht. Unsere Ergebnisse zeigten, dass die Umlaufbahnen des stabilen Gleichgewichts für ihre Rotation (Revolution) für die weitreichende Wechselwirkung induziert werden können; die Abstände zwischen den Teilchen im stabilen Gleichgewicht sind fast die ganzzahligen Vielfachen der Wellenlänge im Medium. Die azimutale optische Kraft verursacht die Orbitaldrehung dieser NPs, und das optische Spin-Drehmoment induziert ihre Drehung, insbesondere die transversalen Komponenten. Diese Bewegung ähnelt der von Doppelsternen gleicher Masse, die sich auf einer Kreisbahn um ihren gemeinsamen Schwerpunkt bewegen. Wenn die Taille eines Gaußschen Strahls kleiner als ein Wendepunkt ist, ist die Helizität der Orbitaldrehung des optisch gebundenen Au-Dimers der Händigkeit des einfallenden CP-Lichts entgegengesetzt. Darüber hinaus wird der Längs-/Quer-SOC signifikant, wenn die Taille eines Gaußschen Strahls abnimmt; daher wird der transversale Spin der beiden NPs tiefer. Bei der kurzreichweitigen Wechselwirkung bewirkt die optische Kraft die gegenseitige Anziehung. Folglich drehen sich die beiden gekoppelten plasmonischen NP nicht nur, sondern rotieren auch mit einer spiralförmigen Bahn und kollidieren schließlich. Darüber hinaus liegt die Grenze des interpartikulären Abstands zwischen den langreichweitigen und kurzreichweitigen Wechselwirkungen zweier gekoppelter NPs ungefähr bei einer halben Wellenlänge im Medium. Unsere Ergebnisse zeigten, dass die Größenordnung der optischen Kraft etwa pN beträgt, was mit den anderen Kräften (z. B. der ponderomotorischen Kraft) verglichen werden kann, um den Beitrag zur Bewegung der NPs zu identifizieren. Unsere Ergebnisse könnten den Weg für die Anwendung von SOC auf lichtmanipulierende NPs für die Nanowissenschaften und Nanotechnologie ebnen. Darüber hinaus lohnt es sich, die Korrelation zwischen den optischen Spin- und Bahndrehmomenten der beiden NPs und den Spin- und Bahndrehimpulsdichten des EM-Felds zu untersuchen; ersterer ist definiert durch \(\operatorname{Im}\left(\overline{\mathbf{E}}\times \mathbf{E}\right)/2\omega\) und letzterer in Lit. [23]. Darüber hinaus ist der SOC im verdrillten Nahfeld von Metamaterialien eine Untersuchung wert [40,41,42,43].

Abkürzungen

CP:

Zirkular polarisiert

EM:

Elektromagnetisch

LH:

Linkshänder

LP:

Linear polarisiert

MMP:

Mehrfach-Multipol

Abgeordneter:

Mikropartikel

NP:

Nanopartikel

SOC:

Spin-Bahn-Kopplung