Doppelte Nichtlinearitätskontrolle von Moden- und Dispersionseigenschaften in graphen-dielektrischen plasmonischen Wellenleitern

Hintergrund

Die Plasmonik von Graphen hat aufgrund der einzigartigen elektronischen und optischen Eigenschaften von Graphen im Vergleich zu Metallen breite Aufmerksamkeit auf sich gezogen [1,2,3,4]. Im THz- und Ferninfrarot-Frequenzbereich dominiert der Intraband-Übergang von Elektronen und Graphen verhält sich wie ein Metall. Daher könnten die Oberflächenplasmonenpolaritonen (SPPs) durch Graphen unterstützt werden. Für die Graphen-Dielektrikum-Mehrschicht-Verbundstruktur wurden die Moden Anregung, Kopplung und Ausbreitung von SPPs untersucht. Die quasi-transversale elektromagnetische Mode wurde in einem Graphen-Parallelplatten-Wellenleiter gefunden [5]. Die Kopplung von SPPs wurde in einer Graphen-Dielektrikum-Mehrschichtstruktur untersucht [6, 7]. Bei der periodischen Anordnung der einschichtigen Graphenblätter tritt eine starke Kopplung zwischen den SPPs auf, wenn die Graphenblätter eng angeordnet sind.

Es wurden beträchtliche Anstrengungen unternommen, um die optischen Eigenschaften von Graphen-Dielektrikum-nichtlinearen Verbundstrukturen [8,9,10,11,12] auf ihr großes Potenzial bei der Kontrolle der Lichtausbreitung im Mikro- und Nanobereich zu untersuchen. Für den Fall von einschichtigem Graphen wurden die Oberflächenplasmonen an der Grenzfläche zwischen Graphen und nichtlinearem Substrat vom Kerr-Typ diskutiert [8]. Es wird gezeigt, dass die Wellenlänge von Graphenplasmonen durch Einstellen der nichtlinearen Permittivität von Substraten abgestimmt werden kann. Für die graphen-nichtlineare dielektrische Mehrschichtstruktur wurden die Ausbreitungs- und Lokalisierungseigenschaften von Graphenplasmonen untersucht und die genauen Dispersionsbeziehungen für TM-Oberflächenplasmonen eines Graphen-Parallelplattenwellenleiters erhalten [11]. Die Ausbreitungs- und Lokalisierungslänge werden durch die Anpassung nichtlinearer Permittivitäten bemerkenswert beeinflusst. Kürzlich wurde die Dispersionsbeziehung für die symmetrischen und antisymmetrischen Plasmonenmoden in einer graphenbeschichteten Kerr-Plattenstruktur abgeleitet [12]. Außer dem typischen vorwärts ausbreitenden Modus wurden der symmetrische und der antisymmetrische Modus gefunden.

Basierend auf der starken Nichtlinearität des Graphens wurden mehrere nichtlineare optische Effekte vorhergesagt [13,14,15,16,17]. Nesterovet al. [15] untersuchten die nichtlineare Ausbreitung von Licht in einer Graphen-Monoschicht und fanden heraus, dass eine Graphen-Monoschicht aufgrund der intrinsischen Nichtlinearität von Graphen TE- und TM-räumliches optisches Soliton bei optischen Frequenzen unterstützen kann. In jüngerer Zeit haben Smirnova et al. [16] untersuchten die nichtlinearen Eigenschaften eines mehrschichtigen Stapels von Graphenschichten und leiteten die nichtlinearen Gleichungen ab, die die räumliche Dynamik der nichtlinearen Plasmonen beschreiben. Die bisherigen Studien konzentrierten sich hauptsächlich auf den Einfluss einzelner Nichtlinearitäten auf die Kontrolle der Lichteigenschaften in graphen-dielektrischen Strukturen. Die Idee der dualen Nichtlinearitätssteuerung wurde in den Graphen-basierten photonischen Übergittern [18, 19] eingeführt, in denen die elektrische und rein optische Steuerung photonischer Strahlen mit einer Genauigkeit im tiefen Subwellenlängenbereich erreicht wurde. Die duale Nichtlinearitätskontrolle von Moden- und Dispersionseigenschaften in einer Graphen-Dielektrikum-Plasmonenstruktur lässt jedoch noch viele Fragen offen. Daher betrachten wir in diesem Artikel die Nichtlinearität von Graphen und Dielektrikum gleichzeitig im Graphen-Dielektrikum-Graphen-Wellenleiter und untersuchen den Einfluss der dualen Nichtlinearität auf die Modenkopplungs- und Dispersionseigenschaften.

Methoden

Der Graphen-nichtlineare dielektrische plasmonische Wellenleiter ist in Abb. 1 schematisch dargestellt, eine Graphen-Parallelplatte mit einer Leitfähigkeit σ _g wird bei x . platziert = ± d /2, wobei das Dielektrikum ein Kerr-Medium mit einer Permittivität von ε . ist = ε _L + α |E | ² . In unserer Analyse wird das Graphen aufgrund seiner Dicke auf einer Atomskala als Grenze behandelt. Betrachtet man transversal-magnetische(TM) SPPs, die sich entlang z . ausbreiten Richtung mit einer Ausbreitungskonstante β und zerfällt exponentiell entlang der x Richtung in die Luft bzw. in das nichtlineare Medium.

Schematische Darstellung eines nichtlinearen plasmonischen Graphen-Dielektrikum-Graphen-Wellenleiters

Für die TM-Polarisation wissen wir, dass es drei Feldkomponenten E . gibt _x , E _z , und H _y . Das Magnetfeld H = H _y y und elektrisches Feld E = E _x x + E _z z erfüllen die Gleichungen

wo ε ₀ und μ ₀ sind die elektrische Permittivität und die magnetische Permeabilität des Vakuums. Aus Gl. (2) und ε = ε _L + α |E | ² wir können

Ersetzen von Gl. (5) in Gl. (4) wir haben

Für kubische Gleichung [20, 21]

Die Diskriminante von Gl. (7) ist

Einstellung \( b=-\left({\varepsilon}_L+\alpha {E}_z^2\right),\kern0.5em c=0\), und \( d=-\alpha {\beta}^2 {H}_y^2/\left({\omega}^2{\varepsilon}_0^2\right)\), lässt sich leicht zeigen, dass die Diskriminante von Gl. (6) trifft

Δ < 0 bedeutet, dass die Gl. (6) hat nur eine reelle Lösung. Aus Cardanos Methode [20] wissen wir, dass für die kubische Gleichung Gl. (7) seine echte Wurzel ist

wo p = c − b ² /3, q = d − bc /3 + 2b ³ /27. Unter Verwendung von Gl. (10) erhalten wir die ε . Ersetzen des ε in Gl. (2) und (3) durch die reelle Lösung können die gewöhnlichen Differentialgleichungen numerisch durch ein Relaxationsverfahren gelöst werden.

Ergebnisse und Diskussionen

Aus Kontinuitätsanforderungen von E _z und H _y , die Randbedingungen bei x = ± d /2 erfüllen E _1z = E _2z und H _2j − H _1j = σ _g E _z . Die Oberflächenleitfähigkeit von Graphen σ _g wird durch die Kubo-Formel [22] einschließlich der Interband- und Intraband-Übergangsbeiträge geregelt. Im THz- und Ferninfrarot-Frequenzbereich dominiert der Intraband-Übergangsbeitrag und die Oberflächenleitfähigkeit kann zu einem einfachen Drude-Typ vereinfacht werden als [23]

wo e ist die Elektronenladung, μ _c ist das chemische Potenzial von Graphen, ω ist die Frequenz und τ ist die Momentum-Relaxationszeit. Dieses Modell ist anwendbar bei niedrigen Temperaturgrenzen (k _B T < < μ _c ) bei niedriger Frequenz (ℏω μ _c ). Für die starke Feldbedingung muss der nichtlineare Teil der Leitfähigkeit berücksichtigt werden und die Gesamtleitfähigkeit von Graphen lautet [16]

wo E _τ ist die Tangentialkomponente des elektrischen Feldes und σ ^NL bezeichnet nichtlineare Leitfähigkeit [16]

wo ν _F = 0,95 × 10 ⁸ cm/s ist die Fermi-Geschwindigkeit.

Beim Graphen kann nur im THz- und fernen Infrarot-Frequenzbereich seine Oberflächenleitfähigkeit auf einen einfachen Drude-Typ vereinfacht werden; daher wählen wir die einfallende Wellenlänge als λ = 10 μm . Andere Parameter sind auf die Werte fixiert ε ₁ = 1, ε _L = 2.25, α = 5 × 10 ^− 16 (m/w) ² [24] E _F = 0,27 EV, τ = 1,5 ps. Es ist bekannt, dass es in linearen Graphen-Dielektrikum-Graphen-Strukturen zwei Moden gibt, nämlich symmetrische bzw. antisymmetrische Moden. Im Folgenden werden wir den Einfluss der Nichtlinearität auf die Modenverteilung in den Graphen-Dielektrikum-Verbundstrukturen diskutieren.

Einstellung H ₀ als anfängliche Magnetfeldkomponente an der einfallenden Grenzfläche, durch numerisches Lösen der Gleichungen (1, 2 und 3) die Abhängigkeit der anfänglichen Magnetfeldstärke H ₀ auf der Ausbreitungskonstante β ist in Abb. 2 angegeben. Die normierte Ausbreitungskonstante \({k}_F=\sqrt{\uppi n}\) ist in Einheiten des Fermi-Impulses [25] angegeben, wobei n = 6 × 10 ¹² cm ^− 2 ist die Trägerdichte. Die durchgezogenen Kurven stellen den Fall dar, dass nur die Nichtlinearität des Dielektrikums betrachtet wird, während die gestrichelten Kurven den Fall bezeichnen, dass die Nichtlinearität von Dielektrikum und Graphen gleichzeitig betrachtet wird. Aus Abb. 2 sehen wir, dass die Modeneigenschaften für beide Fälle gleich sind. Es gibt drei Zweige, was bedeutet, dass der nichtlineare plasmonische Wellenleiter drei Moden unterstützen kann. Verglichen mit dem Fall einer einzelnen Nichtlinearität verringerte sich die anfängliche Feldstärke jedoch offensichtlich für den Fall einer dualen Nichtlinearität. Obwohl der nichtlineare plasmonische Graphen-Wellenleiter drei Moden unterstützen kann, ist es unmöglich zu unterscheiden, welcher Zweig symmetrische, antisymmetrische oder asymmetrische Moden bezeichnet. Um die Modeneigenschaften jedes Zweigs zu bestimmen, zeichnen wir die Verteilung des elektrischen Felds und des magnetischen Felds in Verbindung mit A, B, C bzw. D in Abb. 3 auf.

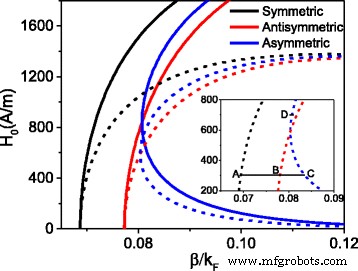
Die anfängliche magnetische Intensität gegenüber der Ausbreitungskonstante. Für die durchgezogenen Kurven :α = 5 × 10 ^− 16 (m /v ) ² , σ ^NL = 0; für die gestrichelten Kurven :α = 5 × 10 ^− 16 (m /v ) ² , σ ^NL = 2,19 × 10 ^− 20 i, die horizontale schwarze durchgehende Linie ist eine Hilfslinie

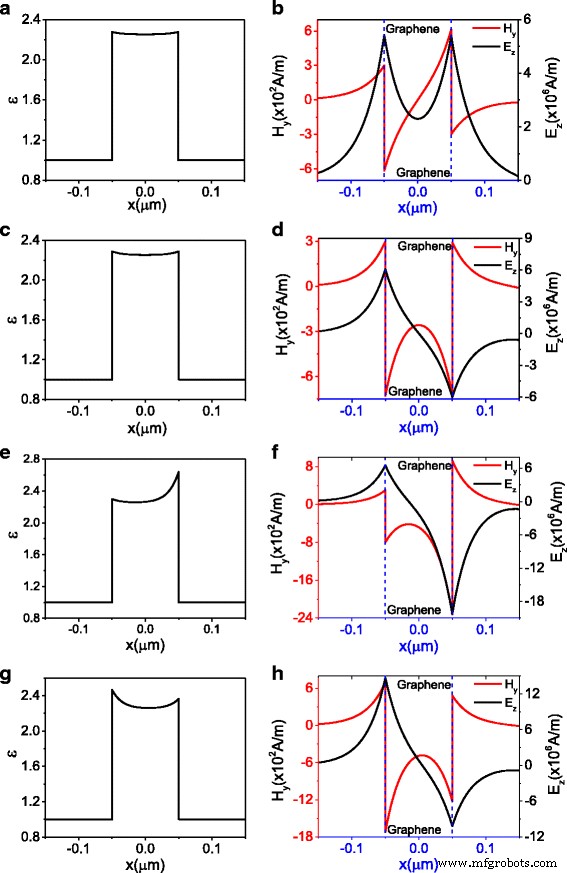
Die Permittivitäts- und Modenverteilung für die magnetische Komponente H _y und elektrische Komponente E _z . a und b entsprechen dem Punkt A (H ₀ = 300, β = 6.94 × 10 ^− 2 k _F ) markiert in Abb. 2 für symmetrische Moden, c und d entsprechen dem Punkt B (H ₀ = 300, β = 7,81 × 10 ^− 2 k _F ) markiert in Abb.2 für antisymmetrische Moden, e und f entsprechen dem Punkt C (H ₀ = 300, β = 8,36 × 10 ^− 2 k _F ) markiert in Abb. 2 für asymmetrische Moden und g und h entsprechen dem Punkt D (H ₀ = 700, β = 8,07 × 10 ^− 2 k _F )

Für den Ast der schwarz-gestrichelten Kurve sind die entsprechende Permittivität und die zu A gehörenden Felder in Abb. 3a, b aufgetragen, wobei die Verteilung der Permittivität und des elektrischen Feldes E _z ist symmetrisch. Daher repräsentiert dieser Zweig den symmetrischen Modus. Für den Zweig der rot gestrichelten Kurve sind die Permittivität und die Felder, die mit B verbunden sind, in Abb. 3c, d angegeben. Die Verteilung der Permittivität ist immer noch symmetrisch; jedoch die Verteilung des elektrischen Feldes E _z ist antisymmetrisch, was bedeutet, dass dieser Zweig ein antisymmetrischer Modus ist. Die Permittivitäts- und Feldverteilung von C und D sind in Abb. 3e–h aufgetragen. Es ist anzumerken, dass die Verteilung des entsprechenden magnetischen Felds und des elektrischen Felds, die C und D zugeordnet sind, asymmetrisch ist; daher repräsentiert der Zweig der blauen gestrichelten Kurve den asymmetrischen Modus. Unterdessen führt die asymmetrische Verteilung des elektrischen Feldes zu der asymmetrischen Verteilung der Permittivität.

Als nächstes wenden wir uns der Diskussion des Einflusses der Nichtlinearität von Dielektrikum und Graphen auf die Dispersionsbeziehung zu. Abbildung 4 zeigt die Dispersionsbeziehung für ein festes anfängliches Magnetfeld (H ₀ = 300 A/m) und unterschiedlichen chemischen Potentialen und nichtlinearen Dielektrizitätskoeffizienten. In Abb. 4a–c ist der Einfluss des nichtlinearen Dielektrikumskoeffizienten auf die Dispersionsrelation dargestellt, wobei nur die Nichtlinearität des Dielektrikums betrachtet wird. Wenn sowohl der nichtlineare Koeffizient als auch die nichtlineare Leitfähigkeit gleich Null sind (α = 0, σ ^NL = 0), entartet die nichtlineare Struktur in eine lineare Struktur. In Fig. 4a existieren für den linearen Fall nur symmetrische und antisymmetrische Moden. Die schwarze durchgehende Kurve und die rote durchgehende Kurve repräsentieren den symmetrischen bzw. antisymmetrischen Modus. Wenn der nichtlineare Koeffizient nicht null ist, erscheint in der Struktur ein asymmetrischer Modus wie der in Fig. 4b, c gezeigte Zweig III. Wenn der nichtlineare Koeffizient weiter ansteigt, wird der Einfluss des Koeffizienten auf die Dispersionseigenschaften schwach.

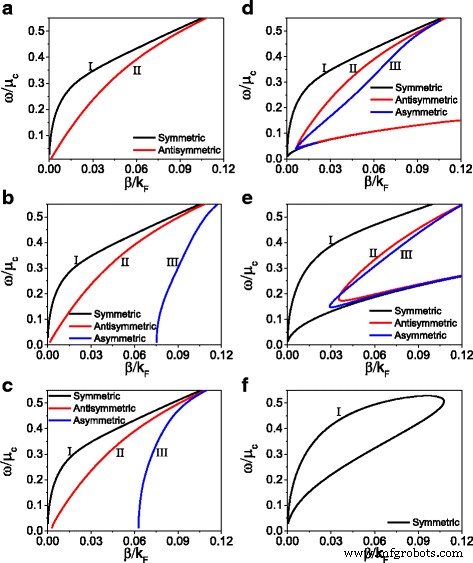
Die Dispersionsbeziehung für eine feste anfängliche magnetische Intensität (H ₀ = 300 A/m) und für verschiedene nichtlineare Koeffizienten(a –c ) und für verschiedene chemische Potenziale (d –f ). a α = 0, μ _c = 0.27eV, σ _NL = 0, b α = 5 × 10 ^− 17 (m/V) ² , μ _c = 0.27eV, σ _NL = 0, c α = 5 × 10 ^− 16 (m/V) ² , μ _c = 0.27eV, σ _NL = 0, d μ _c = 0,27eV, α = 5 × 10 ^− 16 (m/V) ² , (e ) μ _c = 0,16eV, α = 5 × 10 ^− 16 (m/V) ² , und f μ _c = 0,10eV, α = 5 × 10 ^− 16 (m/V) ²

Im Folgenden führen wir gleichzeitig die Nichtlinearität von Dielektrikum und Graphen ein und diskutieren den Einfluss der Nichtlinearität von Graphen auf die Dispersionsrelation mit einem festen nichtlinearen Dielektrizitätskoeffizienten α = 5 × 10 ^− 16 (m/V) ² . Die Ergebnisse sind in Fig. 4d-f gezeigt. Beim Vergleich von Fig. 4d mit Fig. 4c ist festzustellen, dass das Rückfaltungsphänomen der Dispersionsbeziehung in allen drei Zweigen auftritt. Aus Gl. (13) wissen wir, dass die Nichtlinearität des Graphens durch Anpassung des chemischen Potentials gesteuert werden kann. Da die Nichtlinearität von Graphen von μ . weiter zunimmt _c = 0,27 eV zu μ _c = 0,16 eV, wie in Fig. 4e gezeigt, bewegt sich der Rückfaltungspunkt der Dispersionsbeziehung nach oben. Für eine größere Nichtlinearität von Graphen (mit kleinem chemischen Potential μ _c = 0,10 eV), wie in Fig. 4f gezeigt, tritt nur die symmetrische Mode auf und bildet eine geschlossene Schleife. Aus Fig. 4 wissen wir, dass die Dispersionsbeziehung nur unter Berücksichtigung der Nichtlinearität des Dielektrikums drei Zweige aufweist, die mit zunehmendem nichtlinearen Dielektrizitätskoeffizienten nahezu unveränderlich sind. Wenn wir jedoch die Nichtlinearität von Graphen weiter einführen, tritt das Rückfaltungsphänomen der Dispersionsbeziehung auf. Für das angegebene Anfangsmagnetfeld H ₀ und chemischem Potential zeigt die Dispersionsrelation nur eine symmetrische Mode mit geschlossener Schleife.

Schlussfolgerungen

Zusammenfassend haben wir die Moden- und Dispersionseigenschaften von graphen-dielektrischen nichtlinearen plasmonischen Wellenleitern untersucht. Die Modenverteilung, Permittivität und Dispersionsbeziehungen wurden durch numerisches Lösen der Maxwell-Gleichung für die TM-Polarisation erhalten. Verglichen mit dem Fall, in dem nur die Nichtlinearität des Dielektrikums betrachtet wird, verringerte sich die anfängliche Feldstärke offensichtlich, wenn die Nichtlinearität von Dielektrikum und Graphen gleichzeitig berücksichtigt wird. Außerdem beeinflusst die duale Nichtlinearität die Dispersionseigenschaften des Wellenleiters erheblich. Insbesondere wenn die Nichtlinearität des Graphens zunimmt, verschmelzen die antisymmetrischen und asymmetrischen Moden zu einem und verschwinden allmählich. Daher kann bei starker Nichtlinearität nur die symmetrische Mode gefunden werden.