Oberflächenimpedanz von Metaoberflächen/Graphen-Hybridstrukturen

Einführung

In den letzten Jahren wurden in der früheren Literatur [1,2,3,4,5,6] neue künstliche Impedanzmetaoberflächen vorgeschlagen und untersucht, die anomale elektromagnetische Eigenschaften aufweisen. Inzwischen wurden viele Arten von Metaoberflächenanwendungen eingeführt, wie Holographie [1], hochauflösende Bildgebung [2], Teppichumhang [3] und Absorber [4, 5]. Metaoberflächen können eine bedeutende Rolle bei der Realisierung der dünnen Terahertz- und optischen Geräte spielen. Aufgrund der dispersiven Reaktion von Metaoberflächen können viele Geräte jedoch nur in einem einzigen Frequenzband arbeiten und das schmale Spektrum kann nicht abstimmbar sein. Vor kurzem kann die Leitfähigkeit durch Variation der angelegten Spannung in einem breiten Frequenzbereich wie Terahertz oder sogar optischen Frequenzen dynamisch gesteuert werden [7,8,9,10], weshalb Graphen bewiesen hat, dass es der beste Kandidat für die Abstimmung ist die Eigenschaften von plasmonischen und metasurfaces Strukturen [11]. Daher wurden viele Geräte vorgeschlagen, die von Metasurface und Graphen entworfen wurden [12,13,14].

Inzwischen wurden mehrere analytische Modelle zur Berechnung der äquivalenten Impedanz von Metaoberflächen oder Graphenschichten verwendet, um den physikalischen Mechanismus zu erklären [8, 15, 16, 17, 18, 19, 20]. Ebene Wellen zur Anregung von Graphen- oder Metaoberflächenmodellen, die in zwei verschiedene analytische und rechnerische Methoden unterteilt werden können. Die Berechnungsmethode ist die Arbeit am Floquet-Ausdruck [21, 22]. Der Vorteil dieser Methode besteht darin, dass sie nicht auf die Geometrie von Strukturen beschränkt ist und einer der wichtigsten Vorteile darin besteht, dass sie genaue Ergebnisse liefern kann. Dennoch verbraucht kommerzielle Software, die dieses Verfahren verwendet, beträchtliche Zeit und Rechenressourcen. Andererseits wird eine genauere und genauere Analysemethode entwickelt [23,24,25,26,27], die einfach zu handhaben ist und eine bessere Analyse physikalischer Phänomene ermöglicht. Trotz der oben genannten Vorteile stehen auch die Herausforderungen im Vordergrund, ein hochpräzises analytisches Modell für eine bestimmte Metaoberflächeneinheit zu erhalten. Glücklicherweise wurden erhebliche Anstrengungen und Arbeit unternommen, um die äquivalente Oberflächenimpedanz vorherzusagen und viele hervorragende Ergebnisse zu erzielen [16, 28]. Nach Kenntnis der Autoren ist jedoch das analytische Modell, das die Oberflächenimpedanz dieser Hybridkombination vorhersagen kann, noch nicht bekannt.

In diesem Artikel wurde ein künstlicher 3D-Absorber verwendet, um die Impedanz von Metaoberflächen/Graphen-Hybridstrukturen zu analysieren und vorherzusagen, der die Beziehung zwischen Metaoberflächen und Graphen berücksichtigt. Zur schnellen Berechnung der Oberflächenimpedanz von Metaoberflächen wurden zunächst die analytischen Formeln entwickelt. Diese einfachen und präzisen analytischen Formeln können eine vollständige Erläuterung und grundlegende Anforderungen an das Impedanzdesign ermöglichen. Dann werden die Impedanzen der Graphenschichten berechnet. Schließlich konzentrieren wir uns auf die Beziehung zwischen der Größe der Metaoberfläche, dem chemischen Potenzial μ _c und die Impedanz der Verbundstruktur. Hier wird die Oberflächenimpedanz von Metaoberflächen/Graphem-Hybridstruktur durch Berechnung ihrer Real- und Imaginärkomponenten diskutiert. Nach unserem besten Wissen gibt es fast keine Literatur, die diesen Mechanismus umfassend beschreibt.

Methoden

Impedanzen für Square Patches und Graphene Sheets

Eine übliche Struktur eines Metaoberflächen-Graphen-Absorbers ist in Abb. 1a dargestellt. Dieser Absorber mit einfacher Struktur kann leicht durch Oberflächenmikrobearbeitung hergestellt werden. In dieser Konfiguration werden eine dünne leitfähige Metaoberflächen-Graphen-Hybridschicht und die metallische Masseebene durch ein dielektrisches Substrat als Abstandshalter getrennt. Der Abstand zum Boden beträgt h . Für einen kleinen quadratischen Patch im Vergleich zur Wellenlänge (Periode des Arrays D λ ) und Patches werden durch einen schmalen Schlitz getrennt (Breite des Schlitzes D − w ≪ D ) gilt das vorliegende Modell. Gemäß der Übertragungsleitungstheorie kann ein Ersatzschaltungsmodell der absorbierenden Struktur konstruiert werden (in Fig. 1b gezeigt), das das Metaoberflächen-Graphen modellieren kann. Eine Übertragungsleitung, ein Kurzschluss und die Netzimpedanz Z _mg modellieren jeweils den dielektrischen Substratabschnitt, die Masseebene und die Oberflächenimpedanz der oberen strukturierten Hybridschicht. Gemäß der Übertragungsleitungstheorie beträgt die Eingangsimpedanz Z _in dieses Absorbers kann wie folgt festgestellt werden:

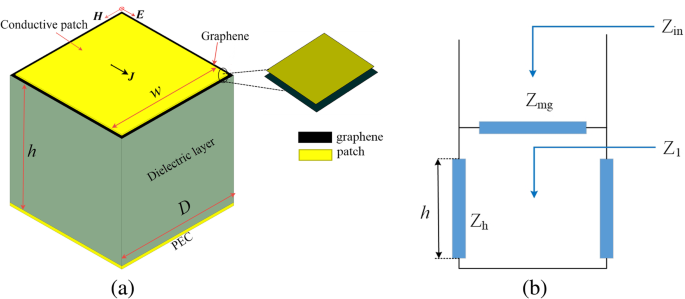
a Schema der Metaoberflächen-Graphen-Absorber-Elementarzelle. b Lokales Ersatzschaltbild

Wo Z _h und k _zh die Impedanz der Substratschichten bzw. die Ausbreitungskonstante in diesem Bereich sind. Dann kann der Absorptionsgrad bei senkrechtem Einfall berechnet werden durch

Es ist offensichtlich, dass die Impedanz der Metaoberflächen-Graphen-Schicht aus dem simulierten Reflexionskoeffizienten extrahiert werden kann. Die Beziehung zwischen der Größe des leitfähigen Flecks und dem chemischen Potential μ _c gefunden werden.

Impedanz für quadratische Patches

Wenn die ebene Welle senkrecht zur Metaoberfläche steht, wirkt die Anordnung planarer Flecken als kapazitives Gitter (wie in Fig. 1a gezeigt). Oberflächenimpedanz Z _m können als elektromagnetische Eigenschaften von quadratischen Feldern veranschaulicht werden, die die durchschnittliche Stromstärke 〈J . in Beziehung setzen 〉 und die gemittelte elektrische Feldstärke 〈E 〉 in der Patchebene:

Bei einer verlustbehafteten rein ohmschen Schichtimpedanz Z _s (im Z_s =0), bei senkrechtem Einfall wird die äquivalente Impedanz des Patches durch Z . dargestellt _m , und kann wie folgt ausgedrückt werden [9, 18]:

Wobei \( {\eta}_{\mathrm{eff}=}\sqrt{\mu_0/{\varepsilon}_0{\varepsilon}_{\mathrm{eff}}} \) die Wellenimpedanz des gleichförmigen Hosts darstellt mittel und D /w ist das geometrische Element. Die effektive relative Permittivität kann angenähert werden als

Außerdem ist der Gitterparameter α für ein elektrisch dichtes Array von ideal leitenden Patches kann geschrieben werden als

\({k}_{\textrm{eff}}={k}_0\sqrt{\varepsilon_{\textrm{eff}}}\) ist die Wellenzahl im effektiven Wirtsmedium. Im freien Speicherplatz μ ₀ , ε ₀ , und k ₀ sind Permeabilität, Permittivität bzw. Wellenzahl. Weiterhin ist darauf hinzuweisen, dass die Beziehung (4) gilt, wenn die Wellenlänge λ ist viel größer als D .

Gemäß Gleichung (2) können wir feststellen, dass die Äquivalenzimpedanz nicht nur durch den spezifischen Schichtwiderstand des Materials bestimmt wird, sondern auch durch die Arrayperiode D und Breite w der Strukturparameter. Um die Sicherheit solcher analytischer Formeln zu überprüfen, werden die Ergebnisse von Vollwellensimulationen präsentiert und mit den analytischen Lösungen verglichen. Die hier diskutierte Simulation wurde unter Verwendung der kommerziell erhältlichen Software Ansoft HFSS durchgeführt. Um die Reflexionseigenschaften der Metaoberflächen-Graphen-Absorber-Elementarzelle zu erhalten, wurden die periodischen Randbedingungen und Floquet-Ports implementiert. Bei seiner Simulation wird die reine ohmsche Schichtimpedanz mit Z _s = 35 Ω/sq wird auf dem Substrat mit der Dicke h . abgeschieden =20 μm, Länge D =20 μm und die relative Permittivität von ε _r = 3.2(1 − j 0,045). Um die Patchimpedanz Z . zu extrahieren _m , entsprechend der Beziehung zwischen der simulierten Eingangsimpedanz Z _in und die Oberflächenimpedanz der geerdeten dielektrischen Platte Z _{g d} , kann die Impedanz des Metaoberflächen-Patches wie folgt ausgedrückt werden:

Wo Z _gd = jZ _d braun(k _d h ), \( {Z}_d=\sqrt{\mu_0/{\varepsilon}_0{\varepsilon}_r}\) ist der Wellenwiderstand der Platte, \( {k}_d=\omega \sqrt{\mu_0 {\varepsilon}_0{\varepsilon}_r} \) ist die Ausbreitungskonstante orthogonal zur Oberfläche des Substrats für den TEM-Modus.

Die analytischen Ergebnisse werden durch Vergleich mit den simulierten basierend auf dem extrahierten Reflexionskoeffizienten verifiziert, wie in Abb. 2 gezeigt. Die schwarzen Kurven zeigen die simulierten Ergebnisse, während die roten Kurven unter Verwendung des vorgeschlagenen analytischen Ausdrucks berechnet werden. Obwohl zwischen den simulierten Ergebnissen und den theoretischen Vorhersagen ein kleiner Unterschied besteht, liegt dies an Gl. (3) ist eine Näherungsgleichung. Der allgemeine Trend ist der gleiche. Dies bestätigt die Gültigkeit und Genauigkeit unseres analytischen Ausdrucks für dieses Modell.

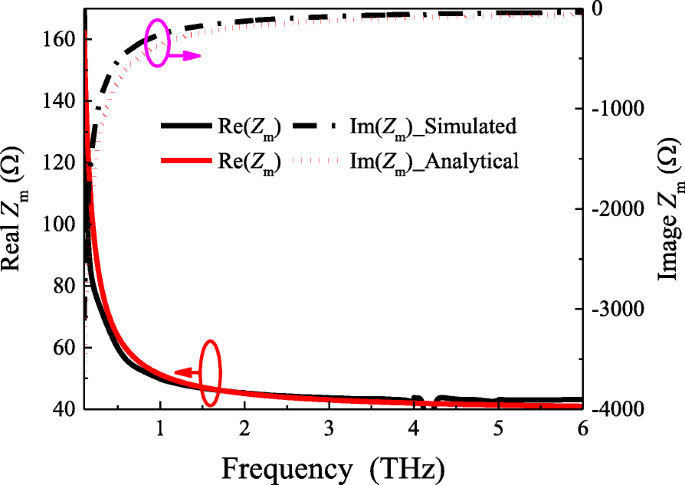
Simulierte und analytische Gitterimpedanzen von Patch-Arrays mit w =19 μm

Um den Einfluss der Patchgrößen auf die Impedanz zu untersuchen Z _m und die Wirksamkeit der Formel (2) validieren, führten wir die zusätzliche numerische Simulation durch. Abbildung 3 zeigt den Real- und Imaginärteil der Netzimpedanz Z _m für verschiedene geometrische Parameter der Elementarzelle. Aus Abb. 3a ist ersichtlich, dass die Realteile der Impedanz Z _m nimmt ab, wenn der Parameter w steigt von 17 auf 19,5 µm. Nach Gl.2 können wir feststellen, dass die Realteile von Z _m sind umgekehrt proportional zur Patchlänge w . Die imaginären Teile zeigen jedoch den entgegengesetzten Trend, wie in gestrichelten Linien gezeigt (in Fig. 3b gezeigt). Unter Berücksichtigung der Gl. (2) und (3) können die Imaginärteile gegeben werden durch

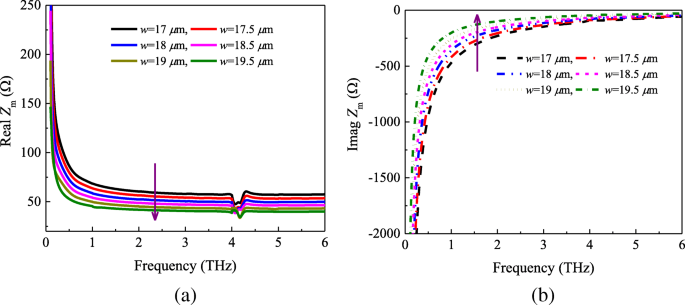
a Echt und b Imaginärteil der Impedanz Z _m mit verschiedenen Patchgrößen

Aus der Beziehung (8) wissen wir, dass wenn w steigt von 17 auf 19,5 µm, die Imaginärteile der Impedanz Z _m wird zunehmen.

Impedanz für Graphenplatten

Graphen kann als unendlich dünne Oberfläche angesehen werden. Wenn keine externe magnetostatische Vorspannung und räumliche Dispersion vorhanden ist, beträgt die Oberflächenleitfähigkeit σ _g , kann berechnet werden durch [29]

Wobei ℏ die reduzierte Planck-Konstante ist, e ist die Ladung eines Elektrons, k _B ist die Boltzmann-Konstante, während μ _c , ω , τ und T sind das chemische Potential, die Winkelfrequenz, die Relaxationszeit bzw. die Temperatur. Hier nehmen wir an T =300 K und τ =0,1 ps während dieser Studie. Die Schichtimpedanz von Graphen kann berechnet werden als

Wo R _g und X _g sind der Oberflächenwiderstand und die Reaktanz.

Die Schichtimpedanz von Graphen wird nach Gl. (9) und (10). Abbildung 4 zeigt die Real- und Imaginärkomponenten der Oberflächenimpedanz gegenüber dem chemischen μ _c . Wir können feststellen, dass der Oberflächenwiderstand und die Reaktanz mit zunehmendem μ . kontinuierlich abnehmen _c . Darüber hinaus bleiben die Realteile des Oberflächenwiderstands der Graphenschicht im Bereich von 0,2–6 THz fast unverändert, wenn das chemische Potenzial auf einen bestimmten Wert festgelegt ist.

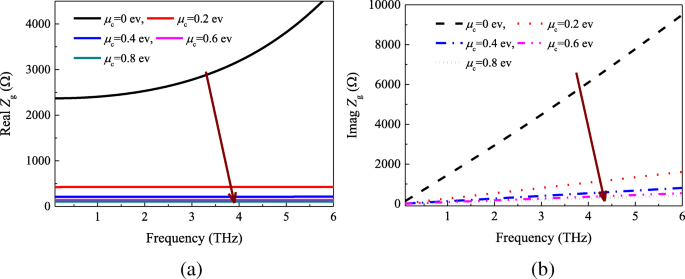
a Echt und b Imaginärteile der Oberflächenimpedanz als Funktion von Frequenz und chemischem Potential

Ergebnisse und Diskussion

Im Fall eines quadratischen Patches auf einer Graphenfolie sollte die Oberflächenimpedanz für diese Hybridstruktur bestimmt werden. In der früheren Literatur [8, 30,31,32,33,34,35,36,37] beträgt die Gesamtimpedanz an der Oberfläche dieser Hybridstruktur Z _mg gleich der Parallelkombination der quadratischen Patchimpedanz Z _m und die Graphenschichtimpedanz Z _g , d. h. Z _mg = Z _m ∥ Z _g . Durch unsere Simulation und Berechnung wird jedoch festgestellt, dass diese Beziehung nicht gültig ist. Um die Authentizität zu verifizieren, simulierten wir eine in Abb. 1a gezeigte Metaoberflächen-Graphen-Absorbereinheit und ermittelten dann die Oberflächenimpedanz des Films gemäß der Gleichung (1). Abbildung 5 zeigt die analytischen und simulierten Werte des Real- und Imaginärteils von Z _mg bei verschiedenen chemischen Potentialen mit w =19 μm.

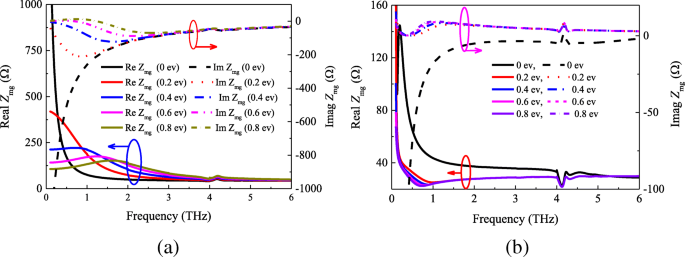
Metaoberflächen-Graphenfilm-Impedanz Z _mg mit unterschiedlichen chemischen Potentialen. a Analytisch und b simulierte Ergebnisse

Aus Abb. 5a, b ist ersichtlich, dass zwischen den analytischen und simulierten Ergebnissen große Unterschiede bestehen. Abbildung 5a zeigt, dass der Realteil der Analyseergebnisse hauptsächlich zwischen 40 und 500 Ω konzentriert war und der Imaginärteil der effektiven Impedanz im Bereich von − 210 bis 0 liegt. Trotzdem können wir gemäß Abb. 5b feststellen, dass die Werte des Realteils der Impedanz von 20 bis 140 Ω und des Imaginärteils nahe 0 liegen, indem wir μ . erhöhen _c von 0 bis 0,8 ev. Die analytischen und simulierten Ergebnisse zeigen jedoch den gleichen Trend, dass die Impedanz mit steigender Frequenz tendenziell stabil bleibt. Der Grund dafür ist, dass die Impedanzen der Graphenschicht und des quadratischen Patches kleiner werden, wenn die Frequenz ansteigt. Es ist bemerkenswert, dass beim Vergleich der Impedanz des Metaoberflächen-Graphenfilms bei 0 eV mit den anderen Ergebnissen die Impedanz Z _mg ist ganz anders. Dies liegt daran, dass sich die Werte der Graphenschichtimpedanz bei 0 eV stark von dem höheren chemischen Potenzial unterscheiden (siehe Abb. 4).

Somit können wir aus der berechneten und simulierten Impedanz in Abb. 5 die folgenden Schlüsse ziehen. Zuerst die Oberflächenimpedanz des Metaoberflächen-Graphenfilms Z _mg ist nicht genau gleich der Parallelkombination von Z _m und Z _g . Zweitens besteht jedoch eine gewisse Beziehung zwischen ihnen. Um diese Schlussfolgerungen zu demonstrieren, simulieren wir zunächst die Struktur des in Abb. 1 gezeigten Absorbers mit unterschiedlichen Patchgrößen. Der Reflexionskoeffizient des Metaoberflächen-Graphen-Absorbers mit dem chemischen Potential μ _c =0,4 ev ist in Abb. 6 dargestellt. Gemäß der Theorie und dem Modell der Übertragungsleitung beträgt die Impedanz Z _mg erhalten werden können. Abbildung 7 zeigt die Real- und Imaginärkomponenten der abgerufenen Impedanz Z _mg mit unterschiedlichen Patchgrößen. Gemäß Abb. 7a kann man sehen, dass der Realteil des Metaoberflächen-Graphen-Films zu Beginn mit der Patchlänge w . abnimmt steigt von 17 µm auf 19,5 µm an. Der gegenteilige Trend wird jedoch festgestellt, wenn die Frequenz höher als 0,31 THz ist. Andererseits zeigt Fig. 7b, dass der Trend des Imaginärteils der gleiche ist wie in der ersten Hälfte von Fig. 7a. Darüber hinaus vergleicht man die Abb. 4 und 5a stellten wir fest, dass in den Fign. 3 und 7. Es beweist auch direkt die obigen Schlussfolgerungen.

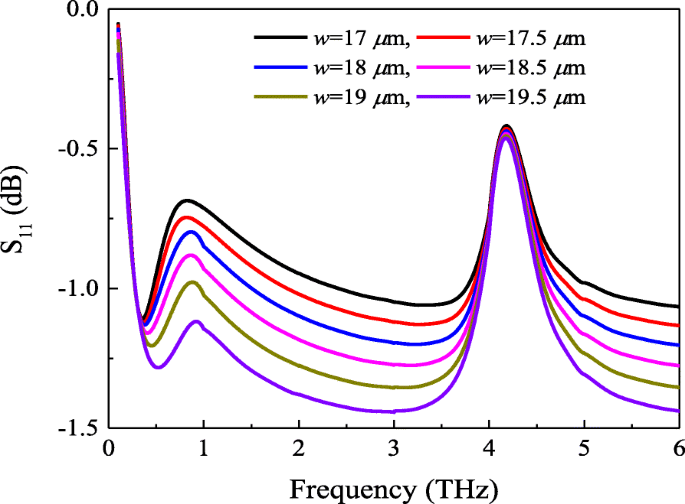
Reflexionskoeffizient des Metaoberflächen-Graphen-Absorbers mit dem chemischen Potential μ _c =0,4 eV

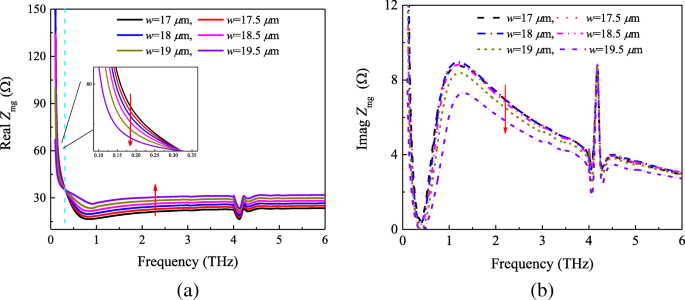
Metaoberflächen-Graphenfilm-Impedanz Z _mg abgerufen von S -Parameter mit dem chemischen Potential μ _c =0,4 ev. a Echt und b imaginäre Teile

Um die physikalischen Ursprünge des Oberflächenwiderstands als Funktion der Patchgröße weiter zu untersuchen, werden die Oberflächenstromverteilungen des Metaoberflächen-Graphenfilms bei senkrechtem Einfall bei 3 THz untersucht. Abbildung 8 zeigt die Variation der Stromstärke für w =17, 18 und 19 μm mit dem chemischen Potenzial μ _c =0,4 Ev. Die Farbe repräsentiert die Intensität des Feldes. Offensichtlich nimmt die Größe des Oberflächenstroms mit zunehmender Größe ab. Unter Berücksichtigung von Gl. 3 und 7a, wenn die elektrische Feldstärke ein fester Wert bei 3 THz ist, kann die Filmimpedanz von Metaoberflächen-Graphen durch $$ {Z}_{mg}\propto w\propto \frac{1}{J}\kern0.5em \left(f>0.32\ \mathrm{THz}\right) $$ (11)

Stärke des Oberflächenstroms bei unterschiedlichen Patch-Größen, aber bei gleicher Frequenz. a w =17 μm, b w =18 μm und c w =19 μm

Aus der Beziehung (11) können wir feststellen, dass die Länge des Flecks umgekehrt proportional zur Größe des Oberflächenstroms ist J . Die qualitative Übereinstimmung zwischen den simulierten und den theoretischen Ergebnissen ist deutlich zu beobachten. Um dieses physikalische Phänomen quantitativ zu analysieren, wird der Integralwert der Oberflächenstromverteilung auf dem Metaoberflächen-Graphenfilm unter Verwendung des HFSS-Feldrechners berechnet, und die Werte sind 1,10e-6, 1,07e-6 und 1,04e-6 A , bzw. Diese Ergebnisse stimmen mit Abb. 8 überein.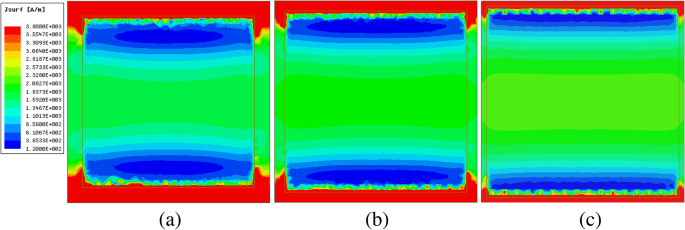

Schlussfolgerungen

Zusammenfassend wurden für einen Metaoberflächen-Graphen-Dünnfilm in der THz-Frequenz die fundamentalen und effektiven Oberflächenimpedanzen untersucht. Zur Berechnung der Impedanz eines quadratischen Patches wurden analytische Formeln abgeleitet und verifiziert. Was die Metaoberflächen-Graphen-Hybridstruktur betrifft, wurden die simulierten Ergebnisse basierend auf dem extrahierten Reflexionskoeffizienten mit den analytischen Ergebnissen verglichen, die aus der parallelen Kombination des quadratischen Patches und der Graphenblattimpedanzen erhalten wurden. Eine zusätzliche Analyse wurde durchgeführt, um den Effekt der Patchgröße auf die effektive Impedanz zu diskutieren. Weiterhin wurden die Zusammenhänge zwischen Patchgröße und Filmimpedanz durch Auftragen und Integrieren des Oberflächenstroms qualitativ und quantitativ erklärt. Diese Analysemethode kann erweitert werden, um das Impedanzproblem mit zwei anderen unterschiedlichen leitfähigen Schichten zu untersuchen. Darüber hinaus können durch unsere in dieser Arbeit durchgeführte Analyse umfangreiche numerische Simulationen sowie analytisch optimierte Verbundschichten für speziell auf Antenne und Absorber aufgebrachte Schichten vermieden werden.

Abkürzungen

HFSS:

Hochfrequenz-Struktursimulation

TEM:

Transversal elektromagnetisch

THz:

Terahertz