Das Design der leitfähigen AZO-Schicht auf einer Mikrokanalplatte

Zusammenfassung

Wenn der spezifische Widerstand der leitfähigen AZO-Schicht innerhalb der MCP-Widerstandsanforderung liegt, ist das Intervall des Zn-Gehalts sehr eng (70–73 %) und schwer zu kontrollieren. Mit Blick auf die Eigenschaften der leitfähigen AZO-Schicht auf der Mikrokanalplatte wurde ein Algorithmus entwickelt, um das Verhältnis des leitfähigen Materials ZnO und des hochohmigen Materials Al2O3 einzustellen. Wir stellen das Konzept des Arbeitswiderstands des MCP (d. h. des Widerstands während der Elektronenlawine im Mikrokanal) vor. Der Arbeitswiderstand von AZO-ALD-MCP (Al2O3/ZnO Atomic Layer Deposition Microchannel Plate) wurde erstmals mit dem MCP-Widerstandstestsystem gemessen. Im Vergleich zum herkömmlichen MCP haben wir festgestellt, dass der Widerstand von AZO-ALD-MCP im Arbeitszustand und im Nicht-Arbeitszustand sehr unterschiedlich ist und mit steigender Spannung der Arbeitswiderstand signifikant abnimmt. Daher haben wir eine Reihe analytischer Methoden für die leitfähige Schicht vorgeschlagen. Wir haben auch vorgeschlagen, das Verhältnis des leitenden Materials der leitenden ALD-MCP-Schicht zu dem hochohmigen Material unter den Arbeitswiderstandsbedingungen einzustellen, und haben erfolgreich AZO-ALD-MCP mit hoher Verstärkung hergestellt. Dieses Design öffnet den Weg, um bessere Materialien für die leitfähige Schicht von ALD-MCP zu finden, um die Leistung von MCP zu verbessern.

Einführung

Mikrokanalplatte (MCP) ist ein Elektronenvervielfacher, der aus zweidimensionalen Porenarrays durch Dünnglasplattenformintegration besteht, Länge von 0,5–5 mm, einen Durchmesser von 4–40 μm und mit einem Neigungswinkel von normalerweise 5°–13° zur Normalen der Plattenoberfläche; das Verhältnis der offenen Fläche der Platte beträgt bis zu 60 % und das hohe Verhältnis von Länge zu Durchmesser in jeder Pore beträgt etwa 20:1 bis 100:1 [1].

Wie in Fig. 1 gezeigt, kollidieren einfallende Elektronen, die in den Mikrokanal eintreten, mit den Wänden, wodurch Sekundärelektronen auf der Oberfläche der Mikrokanalwände erzeugt werden. Mehrfachkollisionen mit den Mikrokanalwänden führen zu einer zunehmenden Anzahl von Sekundärelektronen, was zu einer Elektronenlawine innerhalb des Mikrokanals und der Emission einer Elektronenwolke am Ausgang des Mikrokanals führt. Die Sekundärelektronenelektronen werden entlang des Mikrokanals durch eine Vorspannung weiter beschleunigt. Der MCP-Gewinn beträgt 10³ –10⁴ bei einer Arbeitsspannung von 700–900 V [2,3,4,5,6,7,8,9].

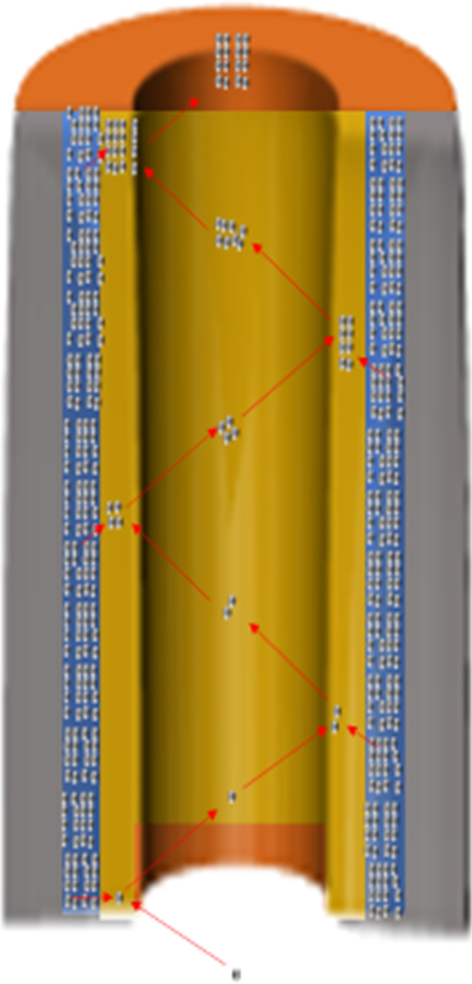
MCP-Arbeitszustandsdiagramm

Jeder Mikrokanal dient als Detektor und Elektronenvervielfacher. Da Millionen von Mikrokanälen unabhängig voneinander arbeiten, hat MCP die Eigenschaften einer hohen räumlichen Auflösung, einer hohen zeitlichen Auflösung und eines breiten Verstärkungsbereichs, der verwendet wird, um Photonen, Elektronen, Neutronen und Ionen zu identifizieren. MCP kann in verschiedene Arten von Instrumenten integriert werden, einschließlich photoelektrischer Detektoren, Photomultiplier-Röhren (PMTs), Ultraviolett-Spektrometer, Kathodenstrahlröhren, Rasterelektronenmikroskope, Feldemissionsanzeigen, Restgasanalysatoren, medizinische Bildgebung, Flugzeit-Massenspektrometrie, Nacht -Sehbrillen usw. [1, 4, 7,8,9]. Die Wasserstoffbefeuerung des traditionellen Prozesses macht den Mikrokanal zu einer geeigneten Leitfähigkeit und einem geeigneten Sekundärelektronenemissionskoeffizienten.

Das übliche Verfahren des Wasserstoffbrennens bei der Herstellung eines Mikrokanals weist viele Nachteile auf:Erstens kann das Wasserstofffeuerungsverfahren die leitfähige Schicht und die Emissionsschicht nicht unabhängig voneinander einstellen [10, 11]; zweitens führen die Schwermetallelemente (Pb, Bi) bei der Bleiglasschmelze zu einer Umweltverschmutzung; drittens verziehen sich große Bereiche des MCP aufgrund der hohen Temperatur [8]; viertens, Bleiglas, das verwendet wird, Wasserstoffreduktionsreaktion enthält K, Rb und andere radioaktive Elemente, was zu Hintergrundrauschen führt [8]; Schließlich wird Wasserstoff, der in den Poren zurückbleibt, aufgrund der Vorspannung zu Ionen, die in die entgegengesetzte Richtung des Elektrons fliegen, um die Kathode des Instruments zu zerstören [8, 12].

Frühe Wissenschaftler schlagen eine Lösung vor, um die leitfähige Schicht und die Emissionsschicht auf der Mikrokanalwand wachsen zu lassen, um den Wasserstoffbrennprozess zu ersetzen [3]. Viele Dünnfilm-Abscheidungsverfahren sind nicht in der Lage, einen gleichförmigen Film in dem Mikrokanal mit hohen Längen-zu-Durchmesser-Verhältnissen zu züchten. Das Argonne National Laboratory schlug vor, Atomic Layer Deposition (ALD) zu verwenden, um die leitfähige Schicht und die Emissionsschicht auf dem MCP wachsen zu lassen, um einen intakten und gleichmäßigen Film auf den Mikrokanalwänden zu erzielen [4, 13]. Darüber hinaus behebt ALD-MCP die oben genannten Mängel. Viele Forschungseinrichtungen sind bestrebt, wettbewerbsfähige Materialien zu finden, die die Leistung von MCP verbessern können.

Das Argonne National Laboratory wählt AZO-Materialien für die leitfähige ALD-MCP-Schicht unter Berücksichtigung der MCP-Widerstandsanforderungen aus. Wenn der Widerstand zu hoch ist, kann die leitfähige Schicht die Elektronen nicht rechtzeitig und kontinuierlich zur Emissionsschicht auffüllen, der MCP weist geringe Verstärkungen auf oder funktioniert sogar nicht. Andererseits, wenn der Widerstand zu niedrig ist, wird das MCP überhitzen, was schließlich zu einem Zusammenbruch führt [4, 9, 14, 15]. Daher ist das Design der leitfähigen Schicht für ein ALD-MCP von Bedeutung.

Wie in Abb. 2 gezeigt, liegt der zulässige Zn-Gehalt in einem sehr engen Bereich (70–73 %) [16], wenn der spezifische Widerstand der leitfähigen AZO-Schicht innerhalb der MCP-Widerstandsanforderung liegt. Daher ist die MCP-Verstärkung instabil und die MCP kann leicht zusammenbrechen. Alternative leitfähige Materialien wie W und Mo anstelle von Zn wurden untersucht [3, 4, 17, 18, 19]. Die chemische Reaktion von ${\text{WF}}_{6}$ (${\text{MoF}}_{6}$) und ${\text{H}}_{2} {\text{O}}$ wird verwendet, um W (Mo) durch ALD zu vergrößern. Die Verwendung von ${\text{WF}}_{6}$ oder ${\text{MoF}}_{6}$ hat jedoch zwei gravierende Nachteile:Sie sind stark korrosiv und enthalten Verunreinigungen, die während des Produktionsprozesses schwer zu entfernen. Aus diesen Gründen ist ALD-MCP mit diesen Materialien teuer.

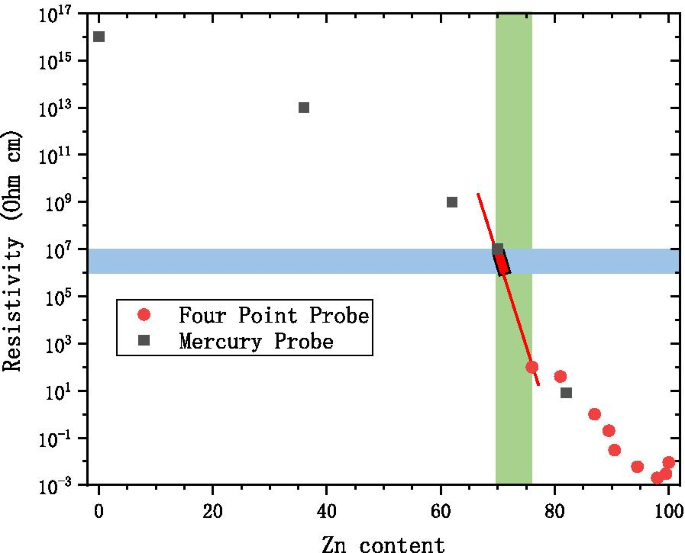
Zn-Gehalt, Zn/(Zn + A)*100(%), blauer Bereich als MCP-Widerstandsbereich, grüner Bereich als AZO-Änderungsbereich, roter Bereich als zu kontrollierender Bereich

In unserer Studie stellen wir fest, dass vernünftige Designs mit ZnO und ${\text{Al}}_{2} {\text{O}}_{3}$ für die leitfähige MCP-Schicht ohne die Herausforderungen wenn W oder Mo verwendet wird, und ist preislich wettbewerbsfähiger. Hier nennen wir das ALD-MCP mit einer AZO-Leitschicht als AZO-ALD-MCP.

Wir schlagen einen Algorithmus vor, um das Verhältnis von leitfähigem Material ZnO und hochohmigem Material ${\text{Al}}_{2} {\text{O}}_{3}$ einzustellen, um unsere gewünschten AZO-Leitschichteigenschaften zu erhalten.

Wir stellen das Konzept des Arbeitswiderstands des MCP (d. h. des Widerstands während der Elektronenlawine im Mikrokanal) vor. Wir haben den Arbeitswiderstand von AZO-ALD-MCP getestet und zwei Unterschiede zwischen AZO-ALD-MCPs und herkömmlichen MCPs gefunden. Wir beobachteten, dass die Arbeits- und Nicht-Arbeitswiderstände sowohl von AZO-ALD-MCPs als auch von konventionellen MCPs signifikant unterschiedlich sind. Außerdem korreliert der Widerstand von AZO-ALD-MLP negativ mit der Spannung. Unser Vorschlag (der Hinweis auf den Arbeitswiderstand) zur Anpassung des Verhältnisses des leitfähigen Materials und des hochohmigen Materials bietet eine Anleitung, die uns bei der Suche nach neuen Materialien zur Verwendung für die leitfähige ALD-MCP-Schicht zur Verbesserung der Leistung des MCP in der Zukunft.

Experiment und Methoden

Wachstum von ZnO und ${\text{Al}}_{2} {\text{O}}_{3}$ Atomfilm

Atomic Layer Deposition (ALD) ist eine Technologie, bei der Vorläufer und reaktive Gase mit einer kontrollierten Geschwindigkeit an der Oberfläche des Substrats zur physikalischen oder chemischen Adsorption oder Oberflächensättigungsreaktion alterniert werden. Das Material wird auf dem Substrat in Form einer monoatomaren Filmoberfläche abgeschieden. ALD kann einen kontinuierlichen Film ohne Pinholes mit ausgezeichneter Abdeckung erzeugen und kann die Dicke und Zusammensetzung des Atomfilms steuern [1, 2, 4, 11, 13, 19, 20].

Im Folgenden sind die chemischen Reaktionsgleichungen für die Verwendung von ALD zum Züchten von Al₂ . aufgeführt O₃ :

$$\begin{ausgerichtet} &{\text{A}}:{\text{Substrat}} - {\text{OH}}^{*} + {\text{Al}}\left( {{\text {CH}}_{3} } \right)_{3} \\ &\quad \to {\text{Substrat}} - {\text{O}} - {\text{Al}}\left( { {\text{CH}}_{3} } \right)_{2}^{*} + {\text{CH}}_{4} \uparrow \\ &{\text{B}}:{\ text{Substrat}} - {\text{O}} - {\text{Al}}\left( {{\text{CH}}_{3} } \right)_{2}^{*} + 2 {\text{H}}_{2} {\text{O}} \\ &\quad \to {\text{Substrat}} - {\text{O}} - {\text{Al}}\left ( {{\text{OH}}} \right)_{2}^{*} + 2{\text{CH}}_{4} \uparrow \\ &{\text{C}}:{\text {Al}} - {\text{OH}}^{*} + {\text{Al}}\left( {{\text{CH}}_{3} } \right)_{3} \\ { } &\quad \to {\text{Al}} - {\text{O}} - {\text{Al}}\left( {{\text{CH}}_{3} } \right)_{ 2}^{*} + {\text{CH}}_{4} \uparrow \\ &{\text{D}}:{\text{Al}} - {\text{CH}}_{3} ^{*} + {\text{H}}_{2} {\text{O}} \to {\text{Al}} - {\text{OH}}^{*} + 2{\text{ CH}}_{4} \uparrow \\ \end{aligned}$$

Die Reaktionstemperatur beträgt 60–150 °C. Wie in Abb. 3 gezeigt, sind die Zeit und die Reihenfolge des Wachsens einer Schicht aus Al₂ O₃ Atom ist:

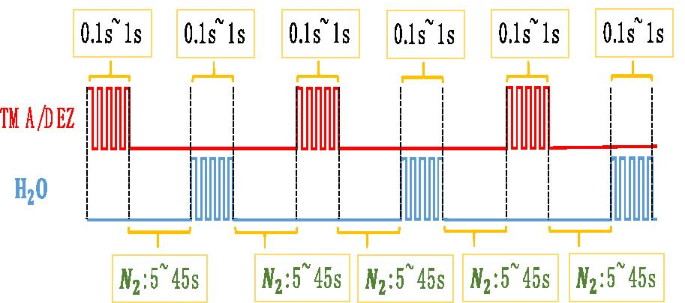
Wachsendes Al₂ O₃ und ZnO-Diagramm

${\text{TMA}}/{\text{N}}_{2} /{\text{H}}_{2} {\text{O}}/{\text{N}}_{ 2} =0,1\sim1{\text{s}}/5\sim45{\text{s}}/0,1\sim1{\text{s}}/5\sim45{\text{s}}$.

Im Folgenden sind die chemischen Reaktionsgleichungen für die Verwendung von ALD zum ZnO-Züchten aufgeführt:

$$\begin{ausgerichtet} &{\text{E}}:{\text{Substrat}} - {\text{OH}}^{*} + {\text{Zn}}\left( {{\text {CH}}_{2} {\text{CH}}_{3} } \right)_{2} \\ &\quad \to {\text{Substrat}} - {\text{O}} - {\text{ZnCH}}_{2} {\text{CH}}_{3}^{*} + {\text{CH}}_{3} {\text{CH}}_{3} \ nach oben \\ &{\text{F}}:{\text{Substrat}} - {\text{O}} - {\text{ZnCH}}_{2} {\text{CH}}_{3} ^{*} + {\text{H}}_{2} {\text{O}} \\ &\quad \to {\text{Substrat}} - {\text{O}} - {\text{ ZnOH}}^{*} + {\text{CH}}_{3} {\text{CH}}_{3} \uparrow \\ &{\text{G}}:{\text{Zn}} - {\text{OH}}^{*} + {\text{Zn}}\left( {{\text{CH}}_{2} {\text{CH}}_{3} } \right) _{2} \\ &\quad \to {\text{Zn}} - {\text{O}} - {\text{ZnCH}}_{2} {\text{CH}}_{3}^ {*} + {\text{CH}}_{3} {\text{CH}}_{3} \uparrow \\ &{\text{H}}:{\text{Zn}} - {\text {CH}}_{2} {\text{CH}}_{3}^{*} + {\text{H}}_{2} {\text{O}} \to {\text{Zn} } - {\text{OH}}^{*} + {\text{CH}}_{3} {\text{CH}}_{3} \uparrow \\ \end{aligned}$$

Die Reaktionstemperatur beträgt 60–150 °C. Wie in Abb. 3 gezeigt, ist der Zeitpunkt und die Reihenfolge des Wachstums einer Schicht aus ZnO-Atom:

$${\text{DEZ}}/{\text{N}}_{2} /{\text{H}}_{2} {\text{O}}/{\text{N}}_{ 2} =0,1\sim1{\text{s}}/5\sim45{\text{s}}/0,1\sim1{\text{s}}/5\sim45{\text{s}}{.}$ $

Design der AZO-Leitschicht

Die Dicke des AZO reicht normalerweise von 300 bis 1000 Atomlagen. Wir definieren eine neue mathematische Operationsregel, um die atomaren Schichtordnungen von Al2O3 und ZnO zu entwerfen, um das Verhältnis des leitfähigen Materials ZnO und des hochohmigen Materials Al2O3 anzupassen.

$$\left(\begin{array}{*{20}c} {{\text{mA}}} \\ {{\text{mB}}} \\ \vdots \\ \end{array} \right )={\text{m}}\left(\begin{array}{*{20}c} {\text{A}} \\ {\text{B}} \\ \vdots \\ \end{array }\right)$$ (1) $$\begin{aligned} &{\text{A}}\left(\begin{array}{*{20}c} {\text{a}} \\ {\ text{b}} \\ \vdots \\ \end{array}\right) + {\text{B}}\left(\begin{array}{*{20}c} {\text{c}} \ \ {\text{d}} \\ \vdots \\ \end{array}\right) + {\text{C}}\left(\begin{array}{*{20}c} {\text{e }} \\ {\text{f}} \\ \vdots \\ \end{array}\right) \ldots \\ &\quad =\left(\begin{array}{*{20}c} {\ text{A}} \\ {\text{B}} \\ \vdots \\ \end{array}\right) \left[ \left(\begin{array}{*{20}c} {\text{ a}} \\ {\text{b}} \\ \vdots \\ \end{array}\right) \left(\begin{array}{*{20}c} {\text{c}} \\ {\text{d}} \\ \vdots \\ \end{array}\right) \left(\begin{array}{*{20}c} {\text{e}} \\ {\text{f }} \\ \vdots \\ \end{array}\right) \ldots \right] =\left(\begin{array}{*{20}c} {{\text{Aa}} + {\text{ Bc}} + {\text{Ce}} + \ldots} \\ {{\text{Ab}} + {\text{Bd}} + {\text{Cf}} + \ldots } \\ \vdots \\ \end{array}\right) \\ \end{aligned}$$ (2)

Die mathematische Operation wurde als WYM-Operation bezeichnet. Die WYM-Operation hat zwei Eigenschaften und eine Formel.

WYM-Eigenschaft 1:

$$\begin{aligned} &\left( {\begin{array}{*{20}c} {\text{m}} \\ {\text{n}} \\ \end{array} } \right )\left[ {\left( {\begin{array}{*{20}c} {\text{a}} \\ {\text{b}} \\ \end{array} } \right)\left ( {\begin{array}{*{20}c} {\text{c}} \\ {\text{d}} \\ \end{array} } \right)} \right]\left[ {\ left( {\begin{array}{*{20}c} {\text{e}} \\ {\text{f}} \\ \end{array} } \right)\left( {\begin{array }{*{20}c} {\text{g}} \\ {\text{h}} \\ \end{array} } \right)} \right]\left[ {\left( {\begin{ array}{*{20}c} {\text{i}} \\ {\text{j}} \\ \end{array} } \right)\left( {\begin{array}{*{20} c} {\text{k}} \\ {\text{l}} \\ \end{array} } \right)} \right] \ldots \\ &\quad =\left( {\begin{array} {*{20}c} {\text{m}} \\ {\text{n}} \\ \end{array} } \right)\left\{ {\left( {\begin{array}{* {20}c} {\text{a}} \\ {\text{b}} \\ \end{array} } \right)\left[ {\left( {\begin{array}{*{20} c} {\text{e}} \\ {\text{f}} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\text{g }} \\ {\text{h}} \\ \end{array} } \right)} \right],\left( {\beg in{array}{*{20}c} {\text{c}} \\ {\text{d}} \\ \end{array} } \right)\left[ {\left( {\begin{array }{*{20}c} {\text{e}} \\ {\text{f}} \\ \end{array} } \right)\left( {\begin{array}{*{20}c } {\text{g}} \\ {\text{h}} \\ \end{array} } \right)} \right]} \right\}\left[ {\left( {\begin{array} {*{20}c} {\text{i}} \\ {\text{j}} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\text{k}} \\ {\text{l}} \\ \end{array} } \right)} \right] \ldots \\ &\quad =\left( {\begin{array}{* {20}c} {\text{m}} \\ {\text{n}} \\ \end{array} } \right)\left[ {\left( {\begin{array}{*{20} c} {\text{a}} \\ {\text{b}} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\text{c }} \\ {\text{d}} \\ \end{array} } \right)} \right]\left\{ {\left( {\begin{array}{*{20}c} {\text {e}} \\ {\text{f}} \\ \end{array} } \right)\left[ {\left( {\begin{array}{*{20}c} {\text{i} } \\ {\text{j}} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\text{k}} \\ {\text{ l}} \\ \end{array} } \right)} \right],\left( {\begin{array}{*{20}c} {\te xt{g}} \\ {\text{h}} \\ \end{array} } \right)\left[ {\left( {\begin{array}{*{20}c} {\text{i }} \\ {\text{j}} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\text{k}} \\ {\text {l}} \\ \end{array} } \right)} \right]} \right\} \ldots \\ \end{aligned}$$

WYM-Eigenschaft 2:

$$\begin{ausgerichtet} &{\text{A}}\left( {\begin{array}{*{20}c} {\text{m}} \\ {\text{n}} \\ \ end{array} } \right)\left[ {\left( {\begin{array}{*{20}c} {\text{a}} \\ {\text{b}} \\ \end{array } } \right)\left( {\begin{array}{*{20}c} {\text{c}} \\ {\text{d}} \\ \end{array} } \right)} \ rechts]\left[ {\left( {\begin{array}{*{20}c} {\text{e}} \\ {\text{f}} \\ \end{array} } \right)\ left( {\begin{array}{*{20}c} {\text{g}} \\ {\text{h}} \\ \end{array} } \right)} \right] \ldots \\ &\quad =\left( {\begin{array}{*{20}c} {{\text{Am}}} \\ {{\text{An}}} \\ \end{array} } \right )\left[ {\left( {\begin{array}{*{20}c} {\text{a}} \\ {\text{b}} \\ \end{array} } \right)\left ( {\begin{array}{*{20}c} {\text{c}} \\ {\text{d}} \\ \end{array} } \right)} \right]\left[ {\ left( {\begin{array}{*{20}c} {\text{e}} \\ {\text{f}} \\ \end{array} } \right)\left( {\begin{array }{*{20}c} {\text{g}} \\ {\text{h}} \\ \end{array} } \right)} \right] \ldots \\ &\quad =\left( {\begin{array}{*{20}c} {\text{m}} \\ {\text{n}} \\ \end{a rray} } \right)\left[ {{\text{A}}\left( {\begin{array}{*{20}c} {\text{a}} \\ {\text{b}} \ \ \end{array} } \right),{\text{A}}\left( {\begin{array}{*{20}c} {\text{c}} \\ {\text{d}} \\ \end{array} } \right)} \right]\left[ {\left( {\begin{array}{*{20}c} {\text{e}} \\ {\text{f} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\text{g}} \\ {\text{h}} \\ \end{array } } \right)} \right] \ldots \\ &\quad =\left( {\begin{array}{*{20}c} {\text{m}} \\ {\text{n}} \ \ \end{array} } \right)\left[ {\left( {\begin{array}{*{20}c} {\text{a}} \\ {\text{b}} \\ \end {array} } \right)\left( {\begin{array}{*{20}c} {\text{c}} \\ {\text{d}} \\ \end{array} } \right) } \right]\left[ {{\text{A}}\left( {\begin{array}{*{20}c} {\text{e}} \\ {\text{f}} \\ \ end{array} } \right),{\text{A}}\left( {\begin{array}{*{20}c} {\text{g}} \\ {\text{h}} \\ \end{array} } \right)} \right] \ldots \\ \end{aligned}$$

WYM-Formel:

$$\begin{aligned} &\left(\begin{array}{*{20}c} {\text{a}} \\ {\text{b}} \\ \vdots \\ \end{array} \right) =\left(\begin{array}{*{20}c} {{\text{A}} + \frac{{\text{X}}}{{\text{Y}}}} \ \ {\text{b}} \\ \vdots \\ \end{array}\right) \propto {\text{Y}}\left(\begin{array}{*{20}c} {{\text {A}} + \frac{{\text{X}}}{{\text{Y}}}} \\ {\text{b}} \\ \vdots \\ \end{array}\right) =\left( {\begin{array}{*{20}c} {{\text{Y}} - {\text{X}}} \\ {\text{X}} \\ \end{array} } \right)\left[ \left(\begin{array}{*{20}c} {\text{A}} \\ {\text{b}} \\ \vdots \\ \end{array}\right ) \left(\begin{array}{*{20}c} {{\text{A}} + 1} \\ {\text{b}} \\ \vdots \\ \end{array} \right) \right] \\ &\left(\begin{array}{*{20}c} {\text{a}} \\ {\text{b}} \\ \vdots \\ \end{array}\right ) =\left(\begin{array}{*{20}c} {\text{a}} \\ {{\text{B}} + \frac{{\text{X}}}{{\text {Y}}}} \\ \vdots \\ \end{array}\right) \propto {\text{Y}}\left(\begin{array}{*{20}c} {\text{a} } \\ {{\text{B}} + \frac{{\text{X}}}{{\text{Y}}}} \\ \vdots \\ \end{array}\right) =\left( {\begin{array}{*{20}c} {{\text{Y}} - {\text{X}}} \\ {\text{X}} \\ \end{array} } \right)\left[ \left(\begin{array}{*{20}c} {\text{a}} \\ {\text{B}} \\ \vdots \\ \end{array}\right ) \left(\begin{array}{*{20}c} {\text{a}} \\ {{\text{B}} + 1} \\ \vdots \\ \end{array}\right) \right] \\ \end{aligned}$$

Beachten Sie, dass Kleinbuchstaben reelle Zahlen darstellen, während Großbuchstaben ganze Zahlen darstellen. In den Beispielen 1 und 2 zeigen wir eine Ausführung der Operation.

Beispiel 1

$$\left( {\begin{array}{*{20}c} {{\text{ZnO}}} \\ {{\text{Al}}_{2} {\text{O}}_{ 3} } \\ \end{array} } \right) =\left( {\begin{array}{*{20}c} {4 + \frac{1}{2}} \\ 1 \\ \end {array} } \right) \propto \left( {\begin{array}{*{20}c} 1 \\ 1 \\ \end{array} } \right)\left[ {\left( {\begin {array}{*{20}c} 4 \\ 1 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} 5 \\ 1 \\ \end{ array} } \right)} \right] =\left( {\begin{array}{*{20}c} 4 \\ 1 \\ \end{array} } \right) + \left( {\begin{ array}{*{20}c} 5 \\ 1 \\ \end{array} } \right)$$

Die Operation wird so interpretiert, dass sie zwei Schemata hat:$\left( {\begin{array}{*{20}c} 4 \\ 1 \\ \end{array} } \right)$ und $\left( {\begin{array}{*{20}c} 5 \\ 1 \\ \end{array} } \right)$. Wachsen Sie für das erste Schema viermal eine ZnO-Atomschicht und eine Al2O3-Atomschicht. Für das zweite Schema wachsen fünfmal eine ZnO-Atomschicht und eine Al2O3-Atomschicht. Wenn wir diese beiden Schemata zweimal wiederholen, erhalten wir die in Abb. 4 gezeigte Struktur.

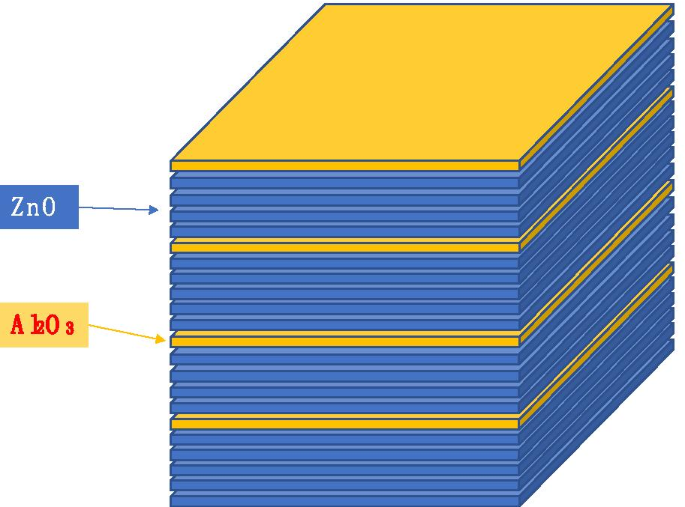
Schematische Darstellung von ZnO und Al₂ O₃ Wachstumssequenz

Eine kompliziertere Verwendung der Operationsregeln wird in Beispiel 2 wie folgt gezeigt:

$$\begin{ausgerichtet} &\left( {\begin{array}{*{20}c} {{\text{ZnO}}} \\ {{\text{Al}}_{2} {\text {O}}_{3} } \\ \end{array} } \right) =\left( {\begin{array}{*{20}c} {4.71} \\ 1 \\ \end{array} } \right) =\left( {\begin{array}{*{20}c} {4 + 0,71} \\ 1 \\ \end{array} } \right) \\ &\frac{2}{3 } =0,666 <0,71 <\frac{3}{4} =0,75 \\ &\left( {\begin{array}{*{20}c} E \\ F \\ \end{array} } \right) \left[ {\left( {\begin{array}{*{20}c} {4 + \frac{2}{3}} \\ 1 \\ \end{array} } \right)\left( { \begin{array}{*{20}c} {4 + \frac{3}{4}} \\ 1 \\ \end{array} } \right)} \right] \\ &\quad =E\ left( {\begin{array}{*{20}c} {4 + \frac{2}{3}} \\ 1 \\ \end{array} } \right) + F\left( {\begin{ array}{*{20}c} {4 + \frac{3}{4}} \\ 1 \\ \end{array} } \right) =\left( {\begin{array}{*{20} c} {4E + 4F + \frac{2}{3}E + \frac{3}{4}F} \\ {E + F} \\ \end{array} } \right) \\ &\quad =E + F\left( {\begin{array}{*{20}c} {4 + \frac{{\frac{2}{3}E + \frac{3}{4}F}}{E + F}} \\ 1 \\ \end{array} } \right) \propto \left( {\begin{array}{* {20}c} {4 + \frac{{\frac{2}{3}E + \frac{3}{4}F}}{E + F}} \\ 1 \\ \end{array} } \right) =\left( {\begin{array}{*{20}c} {4.71} \\ 1 \\ \end{array} } \right) \\ &\frac{{\frac{2}{ 3}E + \frac{3}{4}F}}{E + F} =0,71 \Rightarrow {\text{E}} =12,{\text{F}} =13 \\ &\left( { \begin{array}{*{20}c} E \\ F \\ \end{array} } \right) =\left( {\begin{array}{*{20}c} {12} \\ { 13} \\ \end{array} } \right) =12\left( {\begin{array}{*{20}c} 1 \\ {1\frac{1}{12}} \\ \end{ array} } \right) =\left( {\begin{array}{*{20}c} {11} \\ 1 \\ \end{array} } \right)\left[ {\left( {\begin {array}{*{20}c} 1 \\ 1 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} 1 \\ 2 \\ \end{ array} } \right)} \right] \\ &\left( {\begin{array}{*{20}c} E \\ F \\ \end{array} } \right)\left[ {\left ( {\begin{array}{*{20}c} {4 + \frac{2}{3}} \\ 1 \\ \end{array} } \right),\left( {\begin{array} {*{20}c} {4 + \frac{3}{4}} \\ 1 \\ \end{array} } \right)} \right] \\ &\quad =\left( {\begin{ array}{*{20}c} E \\ F \\ \end{array} } \right)\left[ { \left( {\begin{array}{*{20}c} 1 \\ 2 \\ \end{array} } \right)\left[ {\left( {\begin{array}{*{20}c } 4 \\ 1 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} 5 \\ 1 \\ \end{array} } \right)} \right ],\left( {\begin{array}{*{20}c} 1 \\ 3 \\ \end{array} } \right)\left[ {\left( {\begin{array}{*{20 }c} 4 \\ 1 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} 5 \\ 1 \\ \end{array} } \right)} \right]} \right] \\ &\left( {\begin{array}{*{20}c} {4.71} \\ 1 \\ \end{array} } \right) \propto \left( {\ begin{array}{*{20}c} {12} \\ {13} \\ \end{array} } \right)\left[ {\left( {\begin{array}{*{20}c} 1 \\ 2 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} 1 \\ 3 \\ \end{array} } \right)} \right] \left[ {\left( {\begin{array}{*{20}c} 4 \\ 1 \\ \end{array} } \right)\left( {\begin{array}{*{20}c } 5 \\ 1 \\ \end{array} } \right)} \right] =\left( {\begin{array}{*{20}c} {11} \\ 1 \\ \end{array} } \right)\left[ {\left( {\begin{array}{*{20}c} 1 \\ 1 \\ \end{array} } \right)\left( {\begin{array}{* {20}c } 1 \\ 2 \\ \end{array} } \right)} \right]\left[ {\left( {\begin{array}{*{20}c} 1 \\ 2 \\ \end{array } } \right)\left( {\begin{array}{*{20}c} 1 \\ 3 \\ \end{array} } \right)} \right]\left[ {\left( {\begin {array}{*{20}c} 4 \\ 1 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} 5 \\ 1 \\ \end{ array} } \right)} \right] \\ \end{aligned}$$

Plan 1 :$\left( {\begin{array}{*{20}c} {4.71} \\ 1 \\ \end{array} } \right) \propto 12\left[ {\left( {\begin{ array}{*{20}c} 4 \\ 1 \\ \end{array} } \right) + 2\left( {\begin{array}{*{20}c} 5 \\ 1 \\ \end {array} } \right)} \right] + 13\left[ {\left( {\begin{array}{*{20}c} 4 \\ 1 \\ \end{array} } \right) + 3 \left( {\begin{array}{*{20}c} 5 \\ 1 \\ \end{array} } \right)} \right]$.

Plan 2 $\left( {\begin{array}{*{20}c} {4.71} \\ 1 \\ \end{array} } \right) \propto 11\left[ {\left[ {\left( { \begin{array}{*{20}c} 4 \\ 1 \\ \end{array} } \right) + 2\left( {\begin{array}{*{20}c} 5 \\ 1 \ \ \end{array} } \right)} \right] + \left[ {\left( {\begin{array}{*{20}c} 4 \\ 1 \\ \end{array} } \right) + 3\left( {\begin{array}{*{20}c} 5 \\ 1 \\ \end{array} } \right)} \right]} \right] + \left[ {\left[ { \left( {\begin{array}{*{20}c} 4 \\ 1 \\ \end{array} } \right) + 2\left( {\begin{array}{*{20}c} 5 \\ 1 \\ \end{array} } \right)} \right] + 2\left[ {\left( {\begin{array}{*{20}c} 4 \\ 1 \\ \end{array } } \right) + 3\left( {\begin{array}{*{20}c} 5 \\ 1 \\ \end{array} } \right)} \right]} \right]$.

In Beispiel 2 kann die Operation in Plan 1 wie folgt interpretiert werden:

Schema 1 ALD wachsen viermal ZnO-Atomschicht-Wachstumsprozess und ein ${\text{Al}}_{2} {\text{O}}_{3}$ Atomschicht-Wachstumsprozess; ALD wachsen 5-mal ZnO-Atomschicht-Wachstumsprozess und einen ${\text{Al}}_{2} {\text{O}}_{3}$ Atomschicht-Wachstumsprozess und wiederholen Sie zweimal.

Schema 2 ALD wachsen viermal ZnO-Atomschicht-Wachstumsprozess und ein ${\text{Al}}_{2} {\text{O}}_{3}$ Atomschicht-Wachstumsprozess; ALD wachsen 5-mal ZnO-Atomschicht-Wachstumsprozess und einen ${\text{Al}}_{2} {\text{O}}_{3}$ Atomschicht-Wachstumsprozess und wiederholen Sie dreimal.

Wiederholen Sie Schema 1 12-mal und Schema 2 13-mal.

Die Interpretation der Operation in Plan 2 entspricht der von Plan 1.

Mikrokanal-Plattenwiderstandstest

Wie in Abb. 5a gezeigt, verwenden wir die Atomlagenabscheidungstechnologie, um die AZO-leitfähige Schicht und die ${\text{Al}}_{2} {\text{O}}_{3}$-Emissionsschicht auf Mikrokanalwände der zweidimensionalen Porenanordnungen. Und dann verwenden wir die thermische Verdampfungstechnologie, um die Ni-Cr-Elektrodenschicht auf beiden Seiten des MCP aufzubringen [2, 4] und den Elektrodenring auf beiden Seiten des MCP anzubringen. Als Vorbereitung darauf testen wir direkt die ALD-MCP-Resistenz. In dieser Bedingung definieren wir den entsprechenden MCP-Widerstand als den Nichtgebrauchswiderstand des MCP. Wir verwenden ein Elektrometer des Modells 6517B von Keithley, um den Ruhewiderstand des MCP in einem 10^-3 . zu messen –10⁻⁵ Pa Vakuum [1, 4, 13].

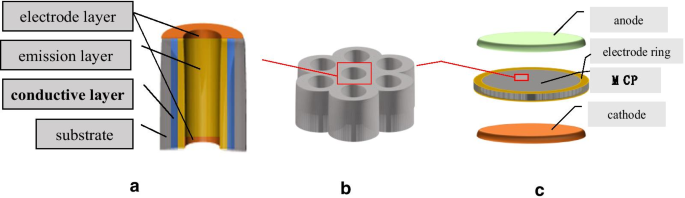
Schematische Darstellung des ALD-MCP-Widerstandstests

Wie in Abb. 5c gezeigt, verwenden wir eine Elektronenkanone als Kathode und einen Phosphorschirm als Anode. Die Elektronenkanone liefert einfallende Elektronen an das MCP, und der Leuchtstoffschirm empfängt die vom MCP ausgegebenen Elektronen. Wenn das MCP in Betrieb ist, emittiert der Hochspannungs-Phosphorschirm außerdem grünes Licht, um die Gleichmäßigkeit des MCP zu erkennen [1, 21].

Wie in Abb. 1 gezeigt, verwenden wir eine Elektronenkanone, die 100 pA als Eingang des MCP bereitstellt, um den Strom zu messen. Aufgrund einer zunehmenden Anzahl von Sekundärelektronen wird es einen Zustand geben, in dem die Emissionsschicht eine große Menge an Ladungen verliert und die leitfähige Schicht kontinuierlich einen Ladungsstrom an die Emissionsschicht liefert. In dieser Bedingung definieren wir den entsprechenden MCP-Widerstand als Arbeitswiderstand des MCP. Die Vakuumumgebung des Arbeitswiderstands beträgt 10^–3 –10⁻⁵ Pa.

Ergebnis und Diskussion

Das Querschnitts-REM-Bild der AZO-ALD-MCP-Probe ist in Abb. 6 dargestellt. Wir haben eine Reihe von AZO-leitfähigen Schichten wie in Tabelle 1 gezeigt und ihre entsprechenden Arbeits- und Nicht-Arbeitswiderstände in Abb. 7 entworfen In der gleichen Abbildung zeigen wir auch die Arbeits- und Nicht-Arbeitswiderstände eines herkömmlichen MCP. Im Vergleich zum Nichtgebrauchswiderstand von AZO-ALD-MCP ist der Gebrauchswiderstand des AZO-ALD-MCP deutlich reduziert. Es gibt jedoch keinen signifikanten Unterschied zwischen dem Arbeitswiderstand und dem Nicht-Arbeitswiderstand eines herkömmlichen MCP. Mit steigender Spannung ist der Arbeitswiderstand von AZO-ALD-MCP deutlich geringer als der eines herkömmlichen MCP. Unter den gleichen Spannungsbedingungen sind die Arbeits- und Ruhewiderstände des AZO-ALD-MCP stabil. Wir glauben, dass es zwei Hauptgründe für die oben genannten Eigenschaften gibt.

Querschnitts-REM-Aufnahme des AZO-ALD-MCP

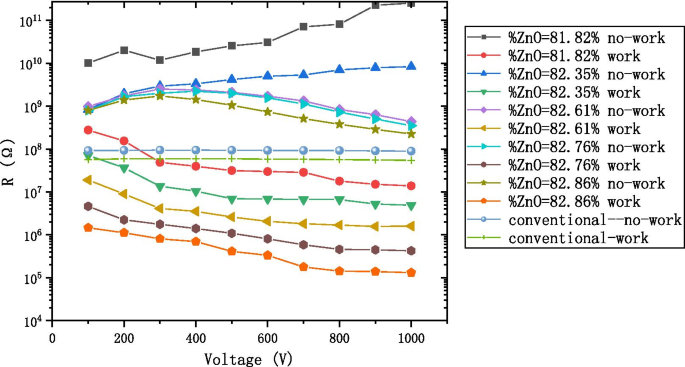
Der Arbeitswiderstand und der Ruhewiderstand mit dem Spannungsdiagramm am AZO-ALD-MCP im unterschiedlichen Verhältnis und konventionellem-MCP

Nach Formel [21],

$$R_{{{\text{MCP}}}} =R_{0} \exp \left[ { - \beta_{T} \left( {T_{{{\text{MCP}}}} - T_{ 0} } \right)} \right]$$

Im Vergleich zu Bleiglas ist AZO ein Material mit einem höheren negativen Temperaturkoeffizienten (NTC), sodass der Widerstand bei gleicher Temperatur und gleichem Anfangswiderstand geringer ist. Bei der Erzeugung von Verstärkung wird AZO von einfallenden Elektronen mit hoher Spannung beschossen, wodurch mehr Elektron-Loch-Paare erzeugt werden, was zu einem Anstieg des Stroms führt.

Wir definieren das Verhältnis von Nichtgebrauchswiderstand zu Gebrauchswiderstand, um die Stabilität des Materialwiderstands zu beschreiben:

$$\kappa_{R} =\frac{{R_{n} }}{{R_{w} }}$$

Abbildung 8 zeigt, dass $\kappa_{R}$ von AZO-ALD-MCP etwa 10² . beträgt –10³ mal, und der $\kappa_{R}$ von konventionellem-MCP ist ungefähr 2–3 mal. Dies zeigt, dass die Widerstandsänderung von AZO-ALD-MCP offensichtlicher ist; Daher sollte das alte Konzept des Nichtgebrauchswiderstands als Definition für den MCP-Widerstand stattdessen durch den Gebrauchswiderstand ersetzt werden.

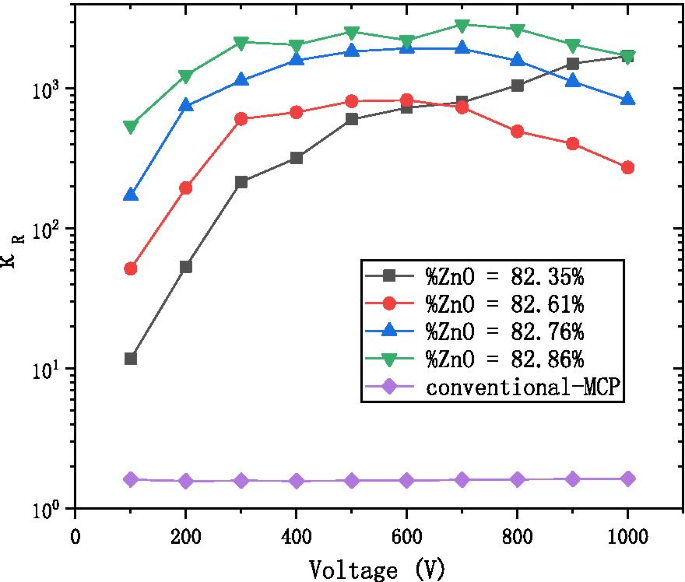
Die K _R mit dem Spannungsdiagramm bei dem unterschiedlichen Verhältnis von AZO-ALD-MCP

Abbildung 9 zeigt das Verhältnis $L_{R}$ des Widerstands aus „benachbartem“ Materialdesign in Bezug auf die Betriebsspannung. Das Verhältnis $L_{R}$ ist definiert als:

$$L_{R} =\frac{{R\left( {4 + \frac{N - 1}{N}} \right)}}{{R\left( {4 + \frac{N}{N + 1}} \right)}}$$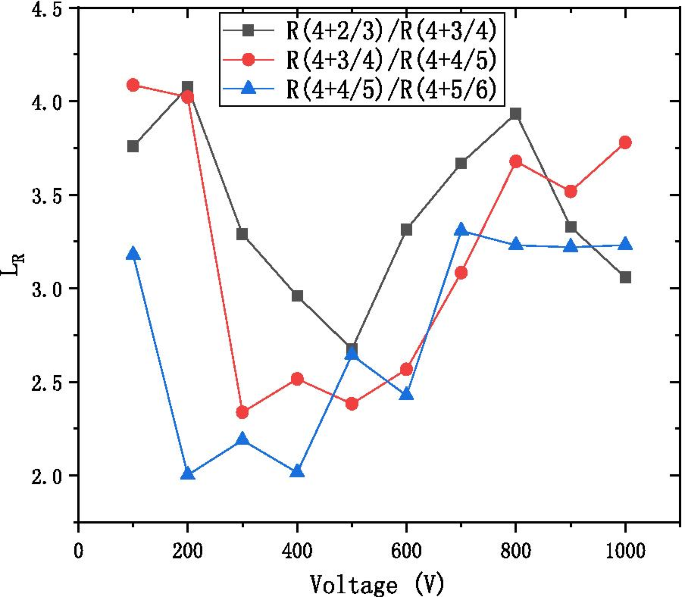

The resistance of the step length L_R with the voltage diagram at the different ratio of the working resistance of neighbor formula

where

$$\left( {\begin{array}{*{20}c} {{\text{ZnO}}} \\ {{\text{Al}}_{2} {\text{O}}_{3} } \\ \end{array} } \right) =\left( {\begin{array}{*{20}c} {4 + \frac{N - 1}{N}} \\ 1 \\ \end{array} } \right) =\left( {\begin{array}{*{20}c} 1 \\ {N - 1} \\ \end{array} } \right)\left[ {\left( {\begin{array}{*{20}c} 4 \\ 1 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} 5 \\ 1 \\ \end{array} } \right)} \right]$$

and

$$\left( {\begin{array}{*{20}c} {{\text{ZnO}}} \\ {{\text{Al}}_{2} {\text{O}}_{3} } \\ \end{array} } \right) =\left( {\begin{array}{*{20}c} {4 + \frac{N}{N + 1}} \\ 1 \\ \end{array} } \right) =\left( {\begin{array}{*{20}c} 1 \\ N \\ \end{array} } \right)\left[ {\left( {\begin{array}{*{20}c} 4 \\ 1 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} 5 \\ 1 \\ \end{array} } \right)} \right]$$

As can be observed from Fig. 9, the L_R value ranges from 2 to 4.5 to adjust ratio of conductive material ZnO and high resistance material ${\text{Al}}_{2} {\text{O}}_{3}$. And it proves the feasibility of WYM operation to design laminated materials.

Figure 10 shows the working resistance with respect to the percentage of ZnO cycles (%ZnO), where %ZnO is defined to be:

$${\text{\% ZnO}} =\frac{{{\text{ZnO}}}}{{{\text{ZnO}} + {\text{Al}}_{2} {\text{O}}_{3} }}{*}100\left( {\text{\% }} \right)$$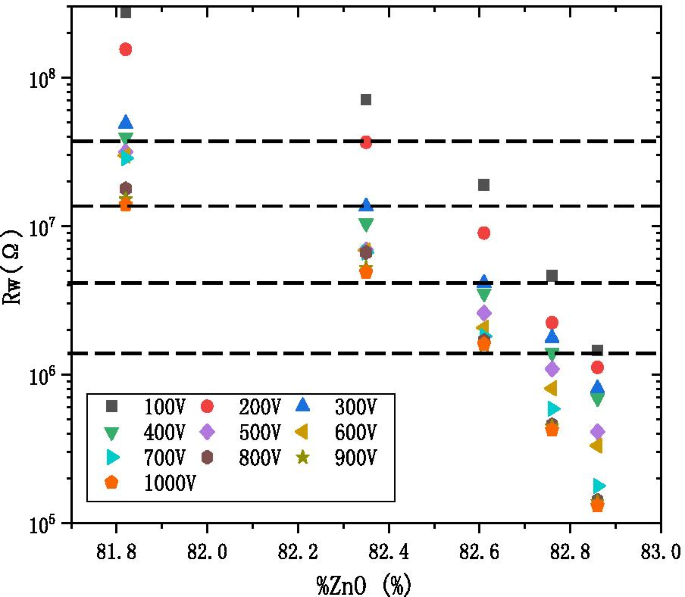

The working resistance with the percentage of ZnO cycles diagram at the different voltage

under various voltage conditions, ranging from 100 to 1000 V. It decreases that the working resistance under the same voltage with the increase in the percentage of ZnO cycles. It can be the same that the working resistance under different the percentage of ZnO cycles and under the different condition of voltage. Therefore, the AZO-ALD-MCP of different formulations works under its specific voltage to meet the MCP resistance index.

We define the ratio of the resistance difference under the different condition of voltage and the voltage difference to describe the effect of the voltage on the resistance of MCP:

$$r =\left| {\frac{{R_{U} - R_{V} }}{U - V}} \right| =\left| {\frac{{R_{1000v} - R_{100v} }}{1000 - 100}} \right|$$

Figure 11 shows that the effect of the voltage on the resistance of AZO-ALD-MCP decreased and gradually stabilized with the increase in the percentage of ZnO cycles. Therefore, the preparation of AZO-ALD-MCP should try to choose a formula with a large percentage of ZnO cycles.

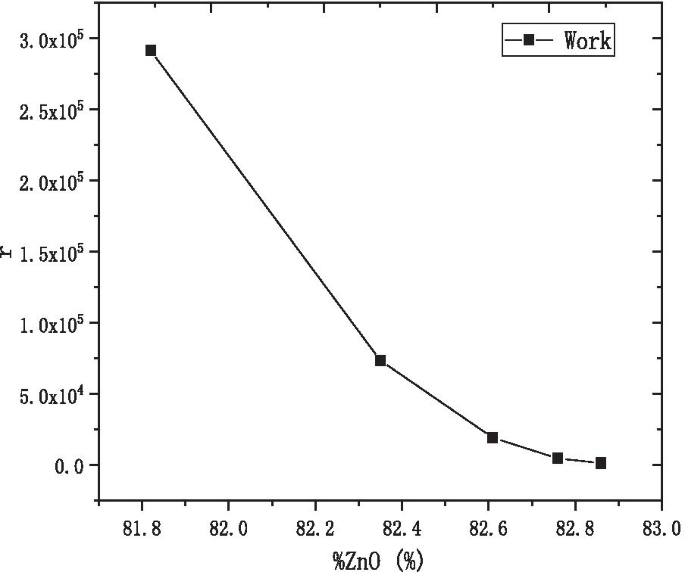
The r with the percentage of ZnO cycles diagram at the working state

Based on the above analysis, we have put forward the reference to the working resistance for the conductive layer of ALD-MCP. As shown in Fig. 5a, we design the AZO conductive layer of AZO-MCP by using the WYM operation and temperature adjustment based on the working resistance. We use atomic layer deposition technology to grow the ${\text{Al}}_{2} {\text{O}}_{3}$ emission layer on microchannel wall of the two-dimensional pore arrays [3, 11, 22]. In Fig. 12a, the gain from our AZO-ALD-MCP is compared to that of a conventional MCP under different voltages. As can be observed, our preparation method of the AZO-ALD-MCP provides a larger gain than that of a conventional MCP. Figure 12b shows the phosphor screen with uniform green light under high pressure, thus proving the uniformity of the material deposited on the wall of each microchannel and the uniformity of the AZO-ALD-MCP field of view.

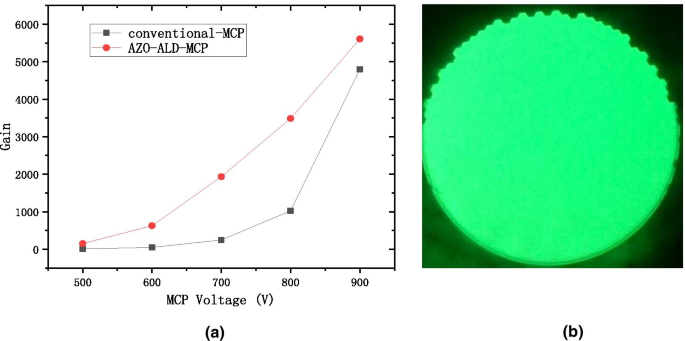
The gain with the voltage diagram at the AZO-ALD-MCP and conventional-MCP

Schlussfolgerung

We defined the working and non-working resistance of the microchannel plate. Aiming at the required resistivity of the microchannel plate in the region with extremely narrow zinc content requirement (70–73%), an algorithm for growing the AZO conductive layer is proposed. Compared with the conventional MCP, we found a large difference between the working and non-working resistance and there is also a huge difference under different voltages. Therefore, we analyze the data by defining $\kappa_{R} ,L_{R} ,\% {\text{ZnO}},r$. MCP should try to choose a formula with a large percentage of ZnO cycles. We recommend using the working resistance as an ALD-MCP resistance indicator in industrial production. Building on our results as described in this work, our studies will help to find even better materials as the conductive layer for the ALD-MCP.