Grundprinzipien der PID-Regelung und Schleifenabstimmung

Der Industriesektor ist stark von PID-Reglern abhängig für alle Arten von Automatisierungsanforderungen. Ein Regelkreis ist ein grundlegender Rückkopplungsmechanismus, der eingesetzt wird, um die Lücke zwischen der gemessenen Prozessvariablen und dem gewünschten Sollwert zu schließen. Controller werden verwendet, um die entsprechenden Korrekturbemühungen über Schnittstellen anzuwenden, die Aktuatoren genannt werden, die die Variable nach oben oder unten treiben können. Der Controller wendet den Korrekturaufwand in einer Schleife an, bis der Fehler bis zur gewünschten Genauigkeit beseitigt ist.

Geschichte

Als die ersten Rückkopplungsregler in Produktion kamen, wurden sie nur mit dem proportionalen Begriff entworfen. Es wurde jedoch bald erkannt, dass Nur-P-Controller den Fehler nur auf einen vernachlässigbaren, aber immer noch einen Wert ungleich Null heruntertreiben konnten. Dazu mussten die Bediener die Verstärkung manuell einstellen, bis die letzte Fehlerspur beseitigt war.

Um diese letzte Aktion automatisch auszuführen, wurde der integrale Begriff eingeführt und oft als automatischer Reset bezeichnet aufgrund seiner Fähigkeit, die Proportionalwirkung einzustellen. Kurz danach wurde der Ableitungsbegriff eingeführt und als Ratenkontrolle beschrieben, die als grober Prädiktor für Fehler fungiert, die basierend auf der aktuellen Fehlersteigung auftreten können.

PID-Grundlagen

Ein PID-Controller verwendet die folgende Formel, um seinen Ausgang zu berechnen, d. h. u(t), wobei e(t) das Fehlersignal ist, das die Differenz zwischen der Prozessvariablen und dem Sollwert ist.

Mit PID-Controllern sind einige Begriffe verbunden; dazu gehören:

• Gewinn – bezieht sich auf den Prozentsatz, um den das Fehlersignal an Stärke gewinnt oder verliert, während es die verschiedenen Blöcke der Controller bis zum Ausgang durchläuft. Wenn beispielsweise ein PID-Regler auf hohe Verstärkung eingestellt ist, würde er auf aggressive Weise Korrekturbemühungen zur Beseitigung des Fehlers durchführen.
• Integralzeit – Eine hypothetische Reihe von Ereignissen kann dazu führen, dass das Fehlersignal abrupt auf einen festen Wert springt, was eine sofortige Reaktion des Proportionalterms des Controllers sowie eine stetig zunehmende Reaktion des Integralterms verhindern würde. Die Zeit, die der Integralterm benötigt, um die unveränderliche Proportionalzeit einzuholen, ist die Integralzeit und wird mit TI bezeichnet.
• Vorhaltezeit – Wenn ein Fehler bei Null beginnt und mit einer festen Rate zunimmt, würde der proportionale Term ebenfalls bei null beginnen, während der derivative Term einen festen Wert annehmen würde. Die Differentialzeit TD ist ein Maß für den relativen Einfluss des Differentialterms, was bedeutet, dass ein PID-Regler mit einer langen Differentialzeit eine stärkere Differentialaktion ausführen würde als ein proportionaler.

Loop-Tuning

Schleifenabstimmung eines PID-Reglers, oft als Kunst bezeichnet, bedeutet die Auswahl von Werten für die Abstimmungsparameter, d. h. P, TI und TD, so dass der Regler in der Lage ist, den Fehler in einer respektablen Zeit zu eliminieren, ohne zu viele Schwankungen zu verursachen .

Der Tempomat eines Autos ist ein gutes Beispiel dafür. Jedes Mal, wenn ein Auto startet, fügt seine Trägheit eine Verzögerung zwischen dem Zeitpunkt hinzu, an dem das Gaspedal gedrückt wird, und dem Zeitpunkt, an dem die gewünschte Geschwindigkeit erreicht wird. Die abgeleiteten und proportionalen Aktionen des Controllers dürfen in diesem Fall nicht sofort eingreifen, sondern auf eine Weise, die für die Passagiere nicht zu unangenehm oder die internen Maschinenteile belasten würde. Wenn die Verzögerung bis zum Erreichen der gewünschten Geschwindigkeit zu lang ist, würde auch die Integralaktion eingreifen und den Ausgang des Reglers dominieren.

Das Einstellen der drei Parameter ist nicht einfach, da alle drei voneinander abhängig sind, was bedeutet, dass die Änderung eines Parameters auch die Leistung der anderen beiden beeinflussen würde.

Ziegler-Nichols-Stimmung

Im Jahr 1942 entwickelten John G. Ziegler und Nathaniel B. Nicholas, die bei Taylor Instruments arbeiteten, eine interessante Methode zur Lösung von Schleifenstimmungsproblemen.

Ihre Open-Loop-Technik besteht darin, den Controller einem Offline-Stufentest zu unterziehen, wonach eine Kurve namens Reaktionskurve entsteht wird basierend auf den Ergebnissen aufgetragen. Am steilsten Punkt der Kurve wird eine Tangente eingezeichnet, die Aufschluss darüber gibt, wie schnell der Prozess auf einen Sprung reagiert. Beide kamen zu folgendem Schluss:

• Die Prozesszeitkonstante T ist der Kehrwert der Steigung der Tangente.
• Die Totzeit d ist die Zeit, die der Prozess benötigt, um seine anfängliche Reaktion auf den Schritt zu demonstrieren.
• Die Prozessverstärkung K gibt an, wie stark die Prozessvariable in Bezug auf die Schrittgröße zunimmt.

Letztendlich entwickelten Ziegler &Nicholas Formeln, die ihnen Werte für die drei Parameter lieferten, d. h. P, TI und TD von T, d und K. Die Formeln lauten:

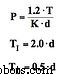
Sobald diese Parameter in die PID-Formel geladen sind und der Regler in den automatischen Zustand versetzt wird, sind keine weiteren Unterbrechungen erforderlich, um Fehler oder Schwankungen zu beseitigen.

Dennoch ist die Abstimmung des PID-Regelkreises kein einfacher Prozess und erfordert Wiederholungen, wann immer sich die Art des Prozesses in irgendeiner Weise ändert. Aus diesem Grund wird Loop-Tuning als Kunst bezeichnet und erfordert eher eine Kombination aus Erfahrung und Glück als rohe mathematische Fähigkeiten!

Möchten Sie mehr erfahren? Sprechen Sie mit einem unserer Experten unter PanelShop.com .

All-In-One-Panels vs. PACs:Was ist das Richtige für Ihre Anwendung? Industrielle Schalttafeln verstehen