Boolesche algebraische Eigenschaften

Eine andere Art von mathematischer Identität, die als „Eigenschaft“ oder „Gesetz“ bezeichnet wird, beschreibt, wie sich unterschiedliche Variablen in einem Zahlensystem zueinander verhalten.

Die Kommutativeigenschaft

Eine dieser Eigenschaften ist als commutative Eigenschaft bekannt , und es gilt gleichermaßen für Addition und Multiplikation.

Im Wesentlichen sagt uns die Kommutativeigenschaft, dass wir die Reihenfolge von Variablen umkehren können, die entweder addiert oder miteinander multipliziert werden, ohne die Wahrheit des Ausdrucks zu ändern:

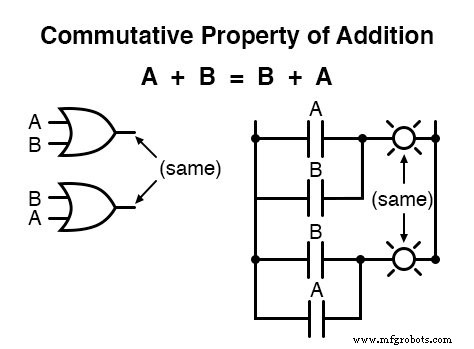
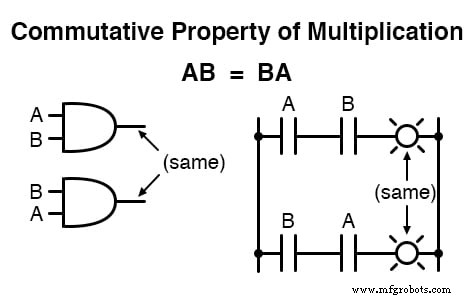
Die assoziative Eigenschaft

Neben den Kommutativeigenschaften der Addition und Multiplikation haben wir die Assoziativeigenschaft , gilt wiederum gleichermaßen für Addition und Multiplikation.

Diese Eigenschaft sagt uns, dass wir Gruppen addierter oder multiplizierter Variablen mit Klammern verbinden können, ohne die Wahrheit der Gleichungen zu ändern.

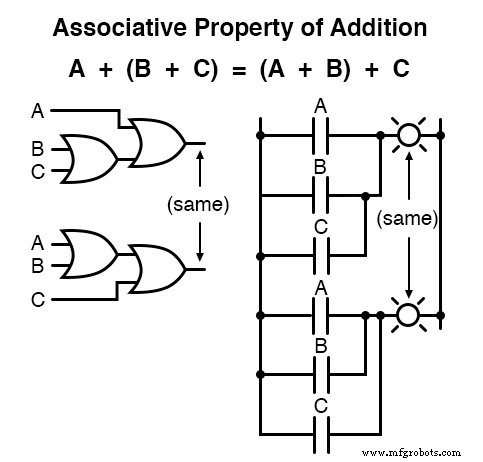
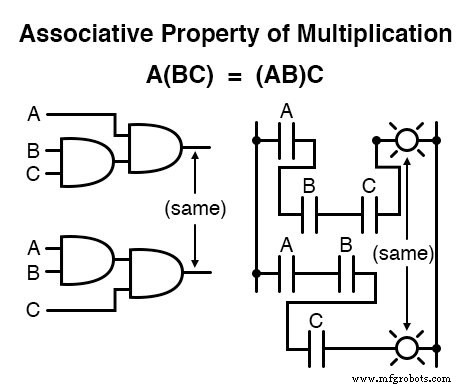
Die Verteilungseigenschaft

Schließlich haben wir die Verteilungseigenschaft , zeigt, wie man einen booleschen Ausdruck erweitert, der durch das Produkt einer Summe gebildet wird, und zeigt uns umgekehrt, wie Terme aus booleschen Produktsummen herausgefiltert werden können:

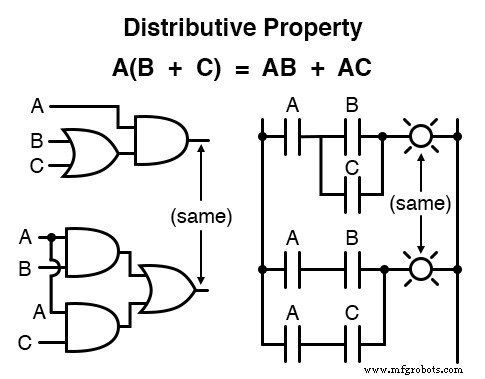
Zusammenfassend sind hier die drei grundlegenden Eigenschaften:kommutativ, assoziativ und distributiv.

VERWANDTE ARBEITSBLÄTTER:

• Arbeitsblatt zur Booleschen Algebra