Boolesche Arithmetik

Beginnen wir unsere Erforschung der Booleschen Algebra, indem wir Zahlen addieren:

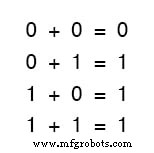
Die ersten drei Summen machen für jeden, der mit elementarer Addition vertraut ist, durchaus Sinn.

Die letzte Summe ist jedoch möglicherweise für mehr Verwirrung verantwortlich als jede andere Einzelaussage in der Digitalelektronik, da sie den Grundprinzipien der Mathematik zu widersprechen scheint.

Nun, es widerspricht den Prinzipien der Addition für reelle Zahlen, aber nicht für boolesche Zahlen.

Denken Sie daran, dass es in der Welt der Booleschen Algebra nur zwei mögliche Werte für jede Größe und für jede arithmetische Operation gibt:1 oder 0.

Es gibt keine „2“ im Bereich boolescher Werte. Da die Summe „1 + 1“ sicherlich nicht 0 ist, muss sie durch Eliminierungsverfahren 1 sein.

Es spielt auch keine Rolle, wie viele oder wenige Begriffe wir zusammenzählen. Betrachten Sie die folgenden Summen:

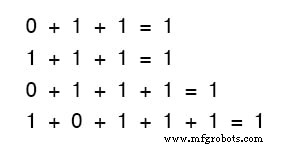
ODER-Gatter

Schauen Sie sich die Zweitermsummen im ersten Gleichungssatz genau an.

Kommt Ihnen dieses Muster bekannt vor? Es sollte! Es ist das gleiche Muster von Einsen und Nullen wie in der Wahrheitstabelle für ein ODER-Gatter.

Mit anderen Worten, die boolesche Addition entspricht der logischen Funktion eines „ODER“-Gatters sowie parallelen Schaltkontakten:

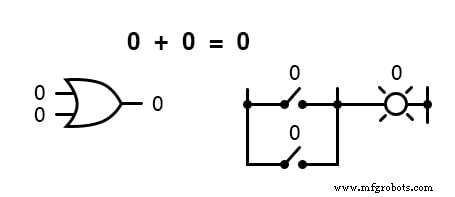
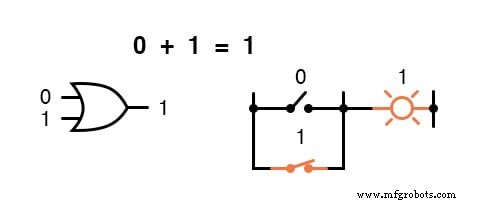
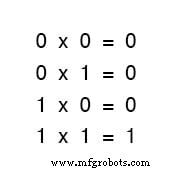
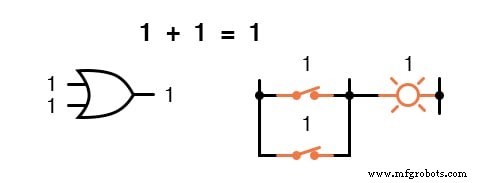
Im Bereich der Booleschen Mathematik gibt es keine Subtraktion.

Subtraktion impliziert die Existenz negativer Zahlen:5 - 3 ist dasselbe wie 5 + (-3) , und in der Booleschen Algebra sind negative Mengen verboten.

Auch in der Booleschen Mathematik gibt es keine Division, da Division eigentlich nichts anderes ist als zusammengesetzte Subtraktion , genauso wie Multiplikation eine zusammengesetzte Addition . ist .

UND-Gatter

Multiplikation ist in der Booleschen Algebra gültig, und glücklicherweise ist sie dasselbe wie in der Algebra mit reellen Zahlen:alles, was mit 0 multipliziert wird ist 0 , und alles multipliziert mit 1 bleibt unverändert:

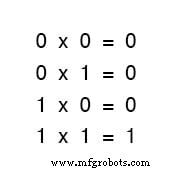
Dieser Satz von Gleichungen sollte Ihnen auch bekannt vorkommen:Es ist das gleiche Muster, das in der Wahrheitstabelle für ein UND-Gatter gefunden wird.

Mit anderen Worten, die boolesche Multiplikation entspricht der logischen Funktion eines „UND ” Tor, sowie zu Reihenschaltkontakten:

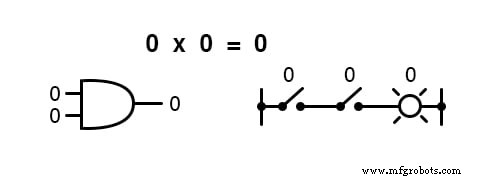
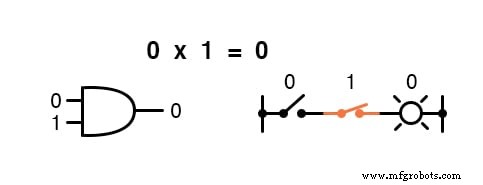
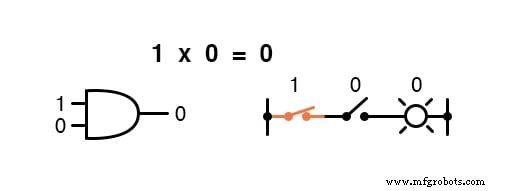
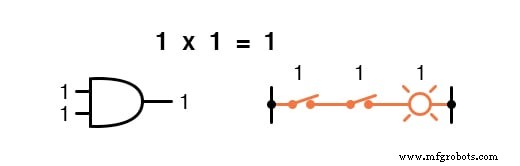
Wie die „normale“ Algebra verwendet die Boolesche Algebra alphabetische Buchstaben, um Variablen zu bezeichnen.

Im Gegensatz zur „normalen“ Algebra sind Boolesche Variablen jedoch immer GROSSBUCHSTABEN, niemals Kleinbuchstaben.

Da sie nur einen von zwei möglichen Werten besitzen dürfen, entweder 1 oder 0 , jede einzelne Variable hat ein Komplement :das Gegenteil von seinem Wert.

Wenn beispielsweise die Variable „A ” hat einen Wert von 0 , dann das Komplement von A hat einen Wert von 1 .

Die boolesche Notation verwendet einen Strich über dem variablen Zeichen, um die Komplementation anzuzeigen, wie folgt:

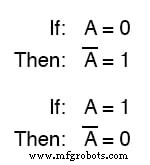
NICHT Tor

In schriftlicher Form die Ergänzung „A “ bezeichnet als „A-nicht “ oder „A-Balken “. Manchmal wird ein „Prime“-Symbol verwendet, um die Komplementation darzustellen.

Beispiel:A ’ wäre die Ergänzung von A , ähnlich wie bei der Verwendung eines Primsymbols, um die Differenzierung in der Infinitesimalrechnung anzugeben, anstatt der Bruchschreibweise d/dt .

Normalerweise findet das „Balken“-Symbol jedoch eine weiter verbreitete Verwendung als das „Prime . ”-Symbol, aus Gründen, die später in diesem Kapitel noch deutlicher werden.

Boolesche Komplementierung findet Äquivalenz in Form des NOT-Gatters , oder ein Öffner oder Relaiskontakt:

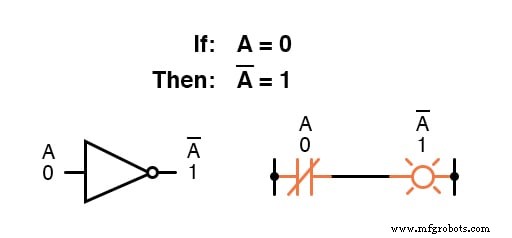
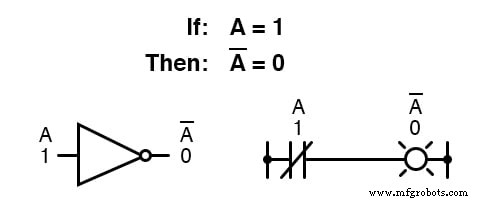
Die grundlegende Definition boolescher Größen hat zu den einfachen Regeln der Addition und Multiplikation geführt und sowohl Subtraktion als auch Division als gültige arithmetische Operationen ausgeschlossen.

Wir haben eine Symbologie zum Bezeichnen von Booleschen Variablen und ihren Komplementen. Im nächsten Abschnitt werden wir Boolesche Identitäten entwickeln.

RÜCKBLICK:

• Boolesche Addition entspricht dem ODER Logikfunktion, sowie parallele Schaltkontakte.
• Boolesche Multiplikation entspricht dem UND Logikfunktion, sowie Reihenschaltkontakte.
• Boolesche Komplementierung ist äquivalent zu NICHT Logikfunktion, sowie stromlos geschlossen Relaiskontakte.

VERWANDTE ARBEITSBLÄTTER:

• Arbeitsblatt zur Booleschen Algebra