Finite State Machines

Bisher war jede vorgestellte Schaltung eine kombinatorische Schaltkreis. Das bedeutet, dass sein Ausgang nur von seinen aktuellen Eingängen abhängig ist. Vorherige Eingänge für diese Art von Schaltungen haben keinen Einfluss auf den Ausgang.

Es gibt jedoch viele Anwendungen, bei denen unsere Schaltkreise ein „Gedächtnis“ haben müssen; sich an frühere Eingaben zu erinnern und ihre Ausgaben entsprechend zu berechnen. Eine Schaltung, deren Ausgang nicht nur von der aktuellen Eingabe abhängt, sondern auch von der Vorgeschichte der Eingabe, wird als sequentielle Schaltung bezeichnet .

In diesem Abschnitt lernen wir, wie man solche sequentiellen Schaltungen entwirft und baut. Um zu sehen, wie dieses Verfahren funktioniert, verwenden wir ein Beispiel, an dem wir unser Thema studieren.

Nehmen wir also an, wir haben ein digitales Quizspiel, das mit einer Uhr arbeitet und eine Eingabe von einer manuellen Taste liest. Wir möchten jedoch, dass der Schalter nur einen HIGH-Impuls an die Schaltung sendet. Wenn wir die Taste direkt in die Spielschaltung einhaken, sendet sie HIGH für so wenige Taktzyklen, wie unser Finger erreichen kann. Auf einer gemeinsamen Taktfrequenz kann unser Finger nie schnell genug sein.

Das Designverfahren umfasst bestimmte Schritte, die befolgt werden müssen, um die Arbeit zu erledigen:

Schritt 1

Der erste Schritt des Entwurfsverfahrens besteht darin, mit einfachen, aber klaren Worten zu definieren, was unsere Schaltung tun soll:

"Unsere Mission ist es, einen Sekundärkreis zu entwickeln, der beim Drücken der manuellen Taste einen HIGH-Impuls mit einer Dauer von nur einem Zyklus sendet und keinen weiteren Impuls sendet, bis der Knopf gedrückt und erneut gedrückt wird."

Schritt 2

Der nächste Schritt besteht darin, ein Zustandsdiagramm zu entwerfen.

Dies ist ein Diagramm, das aus Kreisen und Pfeilen besteht und die Funktionsweise unserer Schaltung visuell beschreibt. Mathematisch gesehen handelt es sich bei diesem Diagramm, das den Betrieb unserer sequentiellen Schaltung beschreibt, um eine endliche Zustandsmaschine. Beachten Sie, dass dies eine Moore-Finite-State-Maschine ist.

Seine Ausgabe hängt nur von seinem aktuellen Zustand ab, nicht von seiner Eingabe. Dies steht im Gegensatz zur Mealy Finite State Machine, bei der die Eingabe die Ausgabe beeinflusst. In diesem Tutorial wird nur die Moore Finite State Machine untersucht.

Das Zustandsdiagramm unserer Schaltung ist wie folgt:(Abbildung unten)

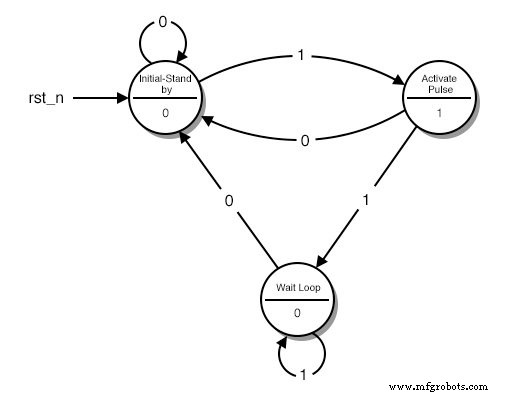
Ein Zustandsdiagramm

Jeder Kreis repräsentiert einen „Zustand“, einen genau definierten Zustand, in dem sich unsere Maschine befindet. In der oberen Hälfte des Kreises beschreiben wir diesen Zustand. Die Beschreibung hilft uns, uns daran zu erinnern, was unsere Schaltung in diesem Zustand tun soll.

• Der erste Kreis ist der „Stand-by“-Zustand. Hier beginnt unsere Schaltung und wartet auf einen weiteren Tastendruck.
• Der zweite Kreis ist der Zustand, in dem die Taste gerade gedrückt wurde und unsere Schaltung einen HIGH-Impuls senden muss.
• Der dritte Kreis ist der Zustand, in dem unsere Schaltung auf das Loslassen der Taste wartet, bevor sie in den "Stand-by"-Zustand zurückkehrt.

Im unteren Teil des Kreises befindet sich der Ausgang unserer Schaltung. Wenn wir möchten, dass unsere Schaltung ein HIGH in einem bestimmten Zustand überträgt, setzen wir eine 1 in diesen Zustand. Ansonsten setzen wir eine 0.

Jeder Pfeil repräsentiert einen „Übergang“ von einem Zustand in einen anderen. Ein Übergang findet einmal in jedem Taktzyklus statt. Abhängig von der aktuellen Eingabe können wir jedes Mal in einen anderen Zustand wechseln. Beachten Sie die Zahl in der Mitte jedes Pfeils. Dies ist die aktuelle Eingabe.

Wenn wir uns zum Beispiel im „Initial-Stand by“-Zustand befinden und eine 1 „lesen“, sagt uns das Diagramm, dass wir in den „Activate Pulse“-Zustand gehen müssen. Wenn wir eine 0 lesen, müssen wir im Zustand „Initial-Stand by“ bleiben.

Was also macht unsere „Maschine“ genau? Er startet aus dem Zustand „Initial - Stand by“ und wartet, bis am Eingang eine 1 gelesen wird. Danach geht er in den Zustand „Activate Pulse“ und sendet an seinem Ausgang einen HIGH-Puls. Wird die Taste weiter gedrückt, geht die Schaltung in den dritten Zustand, die „Warteschleife“.

Dort wartet er, bis der Taster losgelassen wird (Eingang geht auf 0) und sendet dabei ein LOW am Ausgang. Dann ist es wieder vorbei!

Dies ist möglicherweise der schwierigste Teil des Entwurfsverfahrens, da er nicht mit einfachen Schritten beschrieben werden kann. Es braucht Erfahrung und ein bisschen scharfes Denken, um ein Zustandsdiagramm zu erstellen, aber der Rest ist nur eine Reihe von vorgegebenen Schritten.

Schritt 3

Als nächstes ersetzen wir die Wörter, die die verschiedenen Zustände des Diagramms beschreiben durch binär Zahlen. Wir beginnen die Aufzählung bei 0, die dem Anfangszustand zugewiesen wird. Dann setzen wir die Aufzählung mit jedem beliebigen Staat fort, bis alle Staaten ihre Nummer haben. Das Ergebnis sieht in etwa so aus:(Abbildung unten)

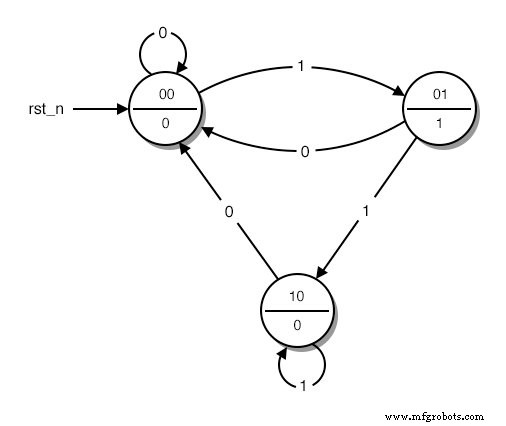
Ein Zustandsdiagramm mit codierten Zuständen

Schritt 4

Danach füllen wir die State Table . Diese Tabelle hat eine ganz bestimmte Form. Ich gebe die Tabelle unseres Beispiels an und verwende sie, um zu erklären, wie man sie ausfüllt. (Abbildung unten)

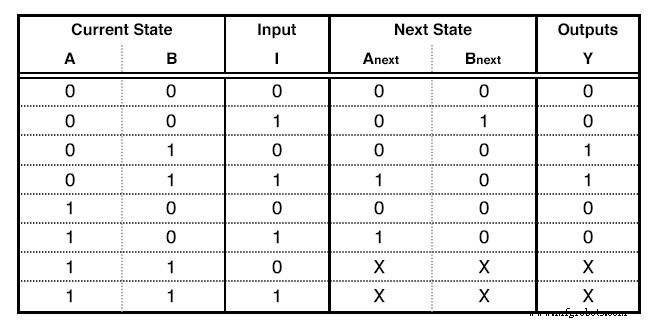
Eine Zustandstabelle

Die ersten Spalten sind so viele wie die Bits der höchsten Zahl, die wir dem Zustandsdiagramm zugewiesen haben. Wenn wir 5 Zustände hätten, hätten wir bis zur Zahl 100 aufgebraucht, was bedeutet, dass wir 3 Spalten verwenden würden. In unserem Beispiel haben wir bis zur Zahl 10 verwendet, sodass nur 2 Spalten benötigt werden. Diese Spalten beschreiben den aktuellen Zustand unserer Schaltung.

Rechts neben den aktuellen Statusspalten schreiben wir die Eingabespalten . Dies sind so viele wie unsere Eingabevariablen. Unser Beispiel hat nur einen Eingang.

Als nächstes schreiben wir die Next State Columns . Dies sind so viele wie die Spalten Aktueller Status.

Schließlich schreiben wir die Ausgabespalten . Das sind so viele wie unsere Outputs. Unser Beispiel hat nur einen Ausgang. Da wir eine More Finite State Machine gebaut haben, hängt die Ausgabe nur von den aktuellen Eingangszuständen ab. Aus diesem Grund enthält die Ausgabespalte zwei 1:um eine boolesche Ausgabefunktion zu erhalten, die unabhängig von Eingabe I ist. Lesen Sie weiter, um weitere Details zu erfahren. Die Spalten Aktueller Status und Eingabe sind die Eingaben unserer Tabelle. Wir füllen sie mit allen Binärzahlen von 0 bis:

2 ^{(Anzahl der Spalten für den aktuellen Status + Anzahl der Eingabespalten)} -1

Es ist zum Glück einfacher als es klingt. Normalerweise gibt es mehr Zeilen als die tatsächlichen Zustände, die wir im Zustandsdiagramm erstellt haben, aber das ist in Ordnung.

Jede Zeile der Next State-Spalte wird wie folgt gefüllt:Wir füllen sie mit dem Zustand, den wir erreichen, wenn wir im State-Diagramm aus dem Current State derselben Zeile der Eingabe derselben Zeile folgen. Wenn Sie eine Zeile ausfüllen müssen, deren aktuelle Statusnummer keinem tatsächlichen Status im Statusdiagramm entspricht, füllen wir sie mit Don’t Care-Begriffen (X). Schließlich ist es uns egal, wohin wir von einem Staat gehen können, der nicht existiert. Wir wären gar nicht da! Auch hier ist es einfacher als es sich anhört.

Die Spalte Ausgaben wird durch die Ausgabe des entsprechenden aktuellen Zustands im Zustandsdiagramm gefüllt.

Die Zustandstabelle ist fertig! Es beschreibt das Verhalten unserer Schaltung genauso vollständig wie das Zustandsdiagramm.

Schritt 5a

Der nächste Schritt besteht darin, diese theoretische „Maschine“ zu nehmen und in eine Schaltung zu implementieren. Meistens beinhaltet diese Implementierung Flip-Flops. Diese Anleitung ist dieser Art der Implementierung gewidmet und beschreibt die Vorgehensweise sowohl für D - Flip Flops als auch für JK - Flip Flops. T - Flip Flops werden nicht aufgenommen, da sie den beiden vorherigen Fällen zu ähnlich sind. Die Auswahl des zu verwendenden Flip-Flops ist willkürlich und wird normalerweise durch Kostenfaktoren bestimmt. Die beste Wahl besteht darin, sowohl eine Analyse durchzuführen als auch zu entscheiden, welcher Flip-Flop-Typ zu einer minimalen Anzahl von Logikgattern und geringeren Kosten führt.

Zuerst werden wir untersuchen, wie wir unsere „Maschine“ mit D-Flip-Flops implementieren.

Wir benötigen so viele D - Flip Flops wie die State-Spalten, in unserem Beispiel 2. Für jedes Flip-Flop fügen wir unserer Zustandstabelle (Abbildung unten) eine weitere Spalte mit dem Namen des Flip-Flops-Eingangs hinzu, in diesem Fall „D“. Die Spalte, die jedem Flip-Flop entspricht, beschreibt welche Eingaben wir dem Flip-Flop geben müssen, um vom aktuellen Zustand zum nächsten Zustand zu gelangen . Für das D - Flip Flop ist das einfach:Der notwendige Input ist gleich dem Next State. In den Zeilen, die X enthalten, füllen wir auch in dieser Spalte Xs aus.

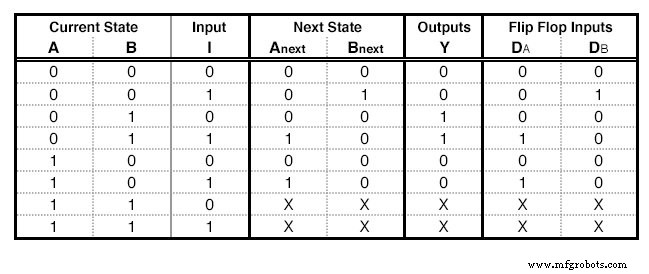
Eine Zustandstabelle mit D - Flip-Flop-Anregungen

Schritt 5b

Wir können die gleichen Schritte mit JK - Flip Flops machen. Es gibt jedoch einige Unterschiede. Ein JK - Flip Flop hat zwei Eingänge, daher müssen wir für jedes Flip Flop zwei Spalten hinzufügen. Der Inhalt jeder Zelle wird durch die Erregungstabelle des JK bestimmt:

Diese Tabelle sagt, dass, wenn wir von State Q zu State Q _nächstes gehen wollen, , müssen wir die spezifische Eingabe für jedes Terminal verwenden. Um beispielsweise von 0 auf 1 zu gehen, müssen wir J mit 1 füttern und es ist uns egal welche Eingabe wir dem Terminal K zuführen.

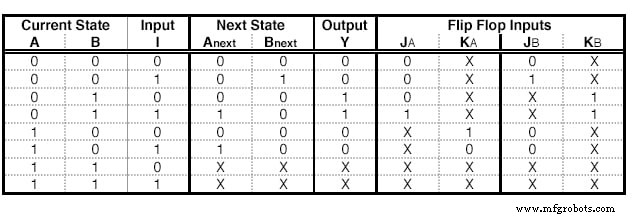
Eine Zustandstabelle mit JK - Flip-Flop-Anregungen

Schritt 6

Wir befinden uns in der letzten Phase unseres Verfahrens. Was bleibt, ist, die booleschen Funktionen zu bestimmen, die die Eingaben unserer Flip-Flops und die Ausgabe erzeugen. Wir extrahieren eine boolesche Funktion für jeden Flip-Flop-Eingang, den wir haben. Dies kann mit einer Karnaugh-Karte erfolgen. Die Eingabevariablen dieser Karte sind die aktuellen Statusvariablen sowie die Eingänge.

Die Eingabefunktionen für unsere D - Flip Flops sind jedoch die folgenden:(Abbildung unten)

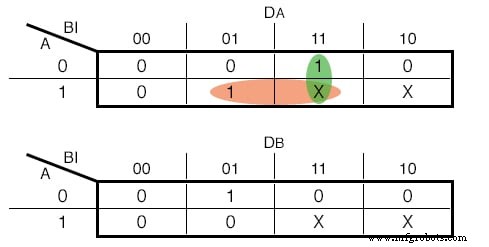
Karnaugh Maps für die D - Flip Flop Eingaben

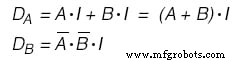
Wenn wir JK - Flip Flops verwenden würden, wären unsere Funktionen die folgenden:(Abbildung unten)

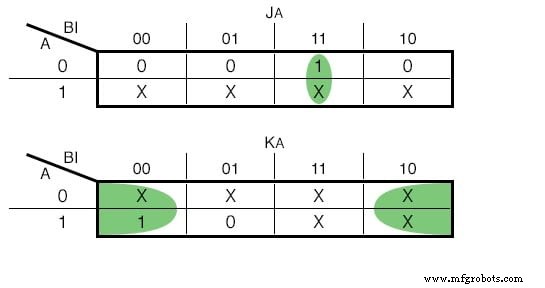
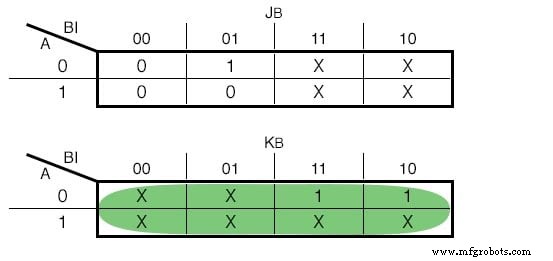
Karnaugh-Karte für den JK - Flip-Flop-Eingabe

Eine Karnaugh-Map wird auch verwendet, um die Funktion des Outputs zu bestimmen:(Abbildung unten)

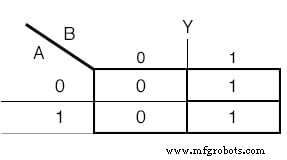
Karnaugh-Map für die Ausgabevariable Y

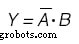
Schritt 7

Wir entwerfen unsere Schaltung. Wir platzieren die Flip-Flops und verwenden logische Gatter, um die von uns berechneten booleschen Funktionen zu bilden. Die Gates nehmen Eingang vom Ausgang der Flip-Flops und vom Eingang der Schaltung an. Vergessen Sie nicht, die Uhr mit den Flip-Flops zu verbinden!

Die D - Flip Flop-Version:(Abbildung unten)

Der fertige D - Flip Flop Sequential Circuit

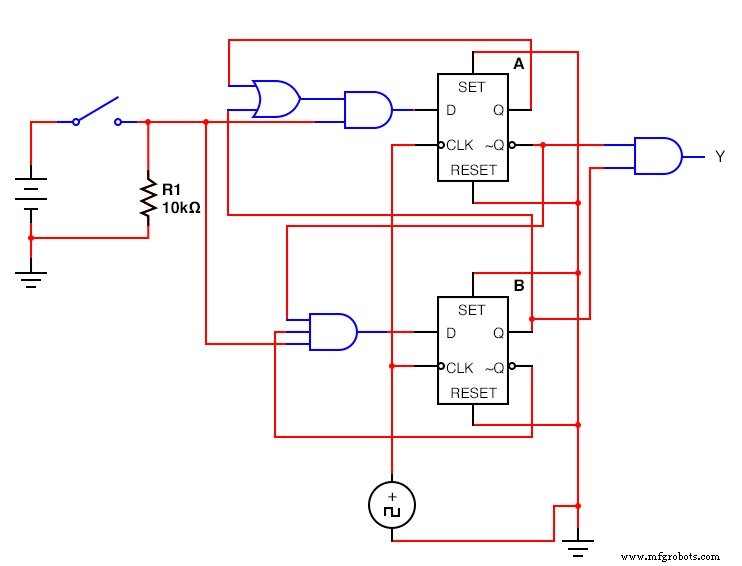
Die JK - Flip Flop Version:(Abbildung unten)

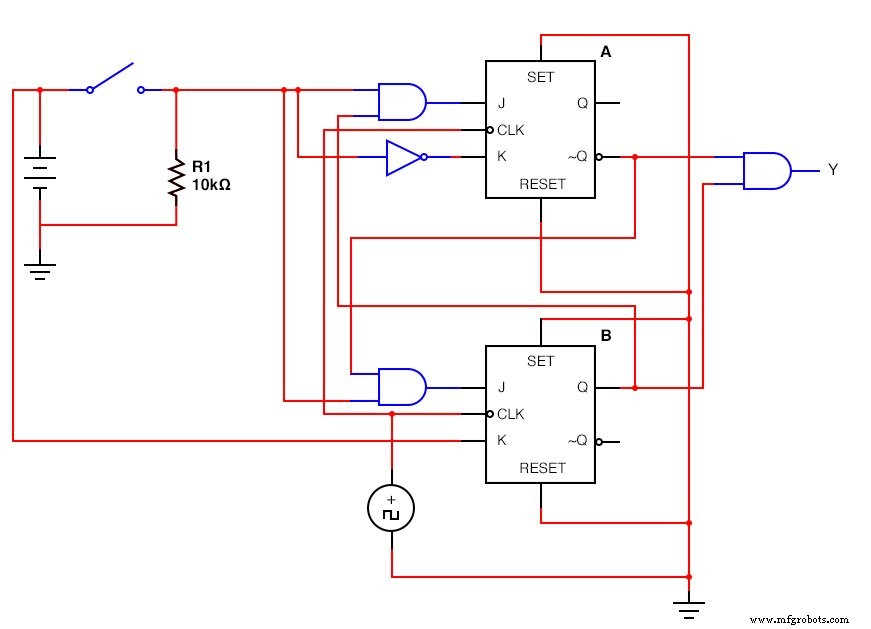
Der fertige JK - Flip Flop Sequential Circuit

Das ist es! Wir haben erfolgreich einen sequentiellen Schaltkreis entworfen und gebaut. Auf den ersten Blick mag es eine entmutigende Aufgabe sein, aber nach Übung und Wiederholung wird das Verfahren trivial. Sequentielle Schaltkreise können sich als Steuerungsteile größerer Schaltkreise als nützlich erweisen und können jede erdenkliche sequentielle Logikaufgabe ausführen. Der Himmel ist die Grenze! (oder zumindest die Platine)

RÜCKBLICK:

• Eine sequentielle Logikfunktion hat eine „Speicher“-Funktion und berücksichtigt vergangene Eingaben, um über die Ausgabe zu entscheiden.
• Die Finite State Machine ist ein abstraktes mathematisches Modell einer sequentiellen Logikfunktion. Es hat endliche Eingänge, Ausgänge und eine Anzahl von Zuständen.
• FSMs werden durch die Verwendung von Flip-Flops in realen Schaltungen implementiert
• Das Implementierungsverfahren benötigt eine bestimmte Reihenfolge von Schritten (Algorithmus), um ausgeführt zu werden.