Einige Beispiele mit Wechselstromkreisen

Lassen Sie uns drei Wechselspannungsquellen in Reihe schalten und komplexe Zahlen verwenden, um additive Spannungen zu bestimmen.

Alle Regeln und Gesetze, die man im Studium von Gleichstromkreisen gelernt hat, gelten auch für Wechselstromkreise (Ohmsches Gesetz, Kirchhoffsche Gesetze, Netzanalyseverfahren), mit Ausnahme von Leistungsberechnungen (Joulesches Gesetz).

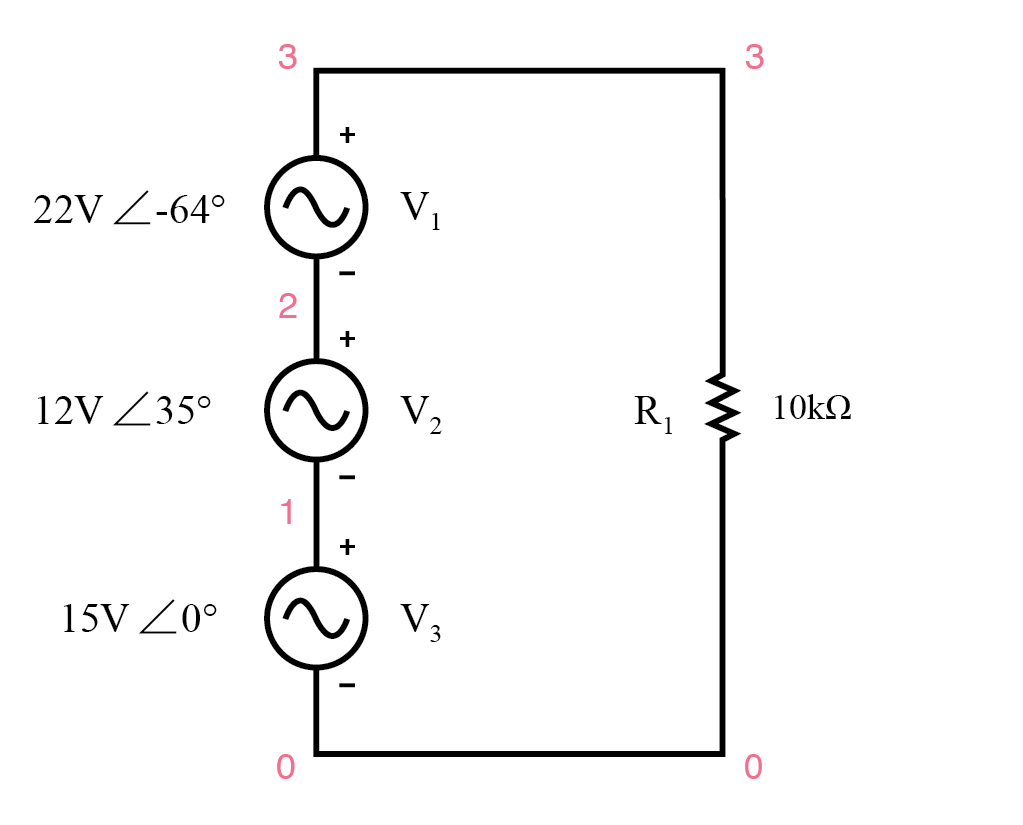
Die einzige Einschränkung besteht darin, dass alle Variablen müssen komplex ausgedrückt werden, wobei sowohl Phase als auch Betrag berücksichtigt werden, und alle Spannungen und Ströme müssen die gleiche Frequenz haben (damit ihre Phasenbeziehungen konstant bleiben). (Abbildung unten)

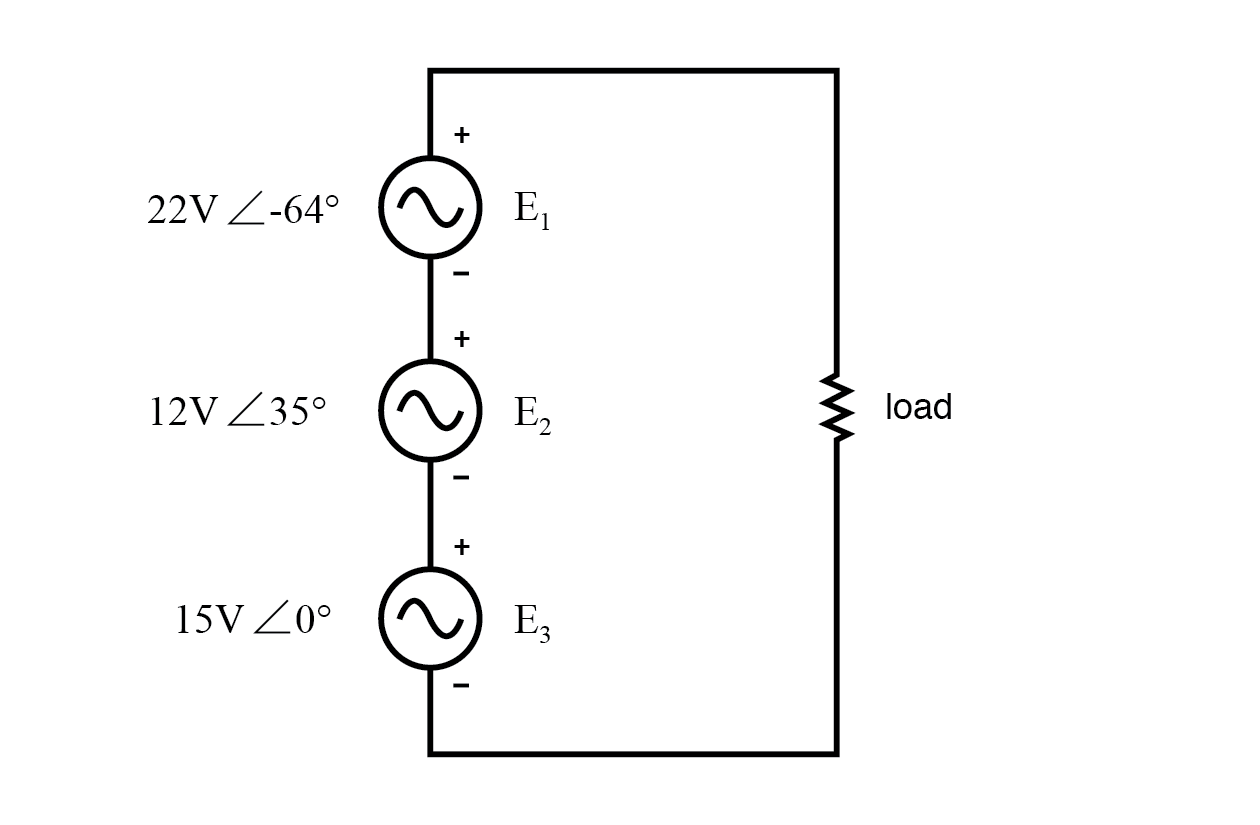
KVL ermöglicht die Addition komplexer Spannungen.

Die Polaritätsmarkierungen für alle drei Spannungsquellen sind so ausgerichtet, dass sich ihre angegebenen Spannungen addieren sollten, um die Gesamtspannung am Lastwiderstand zu ergeben.

Beachten Sie, dass, obwohl für jede AC-Spannungsquelle Betrag und Phasenwinkel angegeben sind, kein Frequenzwert angegeben ist. Wenn dies der Fall ist, wird davon ausgegangen, dass alle Frequenzen gleich sind, wodurch unsere Voraussetzungen erfüllt sind, DC-Regeln auf einen AC-Kreis anzuwenden (alle Zahlen in komplexer Form, alle mit der gleichen Frequenz).

Der Aufbau unserer Gleichung zum Ermitteln der Gesamtspannung sieht wie folgt aus:

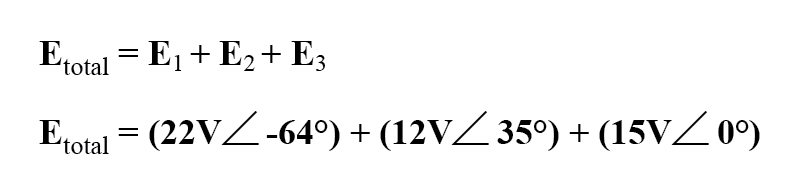
Grafisch addieren sich die Vektoren wie in der Abbildung unten gezeigt.

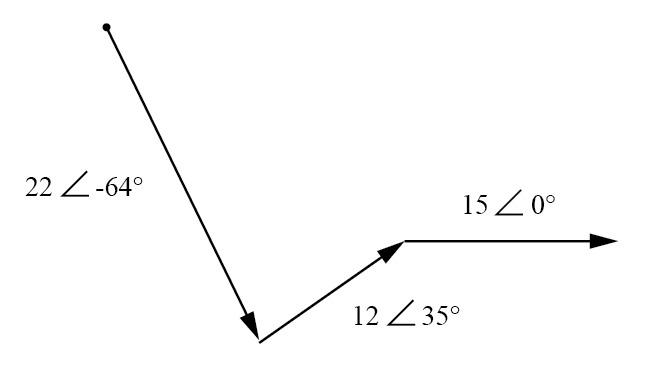
Grafische Addition von Vektorspannungen.

Die Summe dieser Vektoren ist ein resultierender Vektor, der am Startpunkt des 22-Volt-Vektors (der Punkt oben links im Diagramm) beginnt und am Endpunkt des 15-Volt-Vektors endet (Pfeilspitze in der Mitte -rechts im Diagramm):(Abbildung unten)

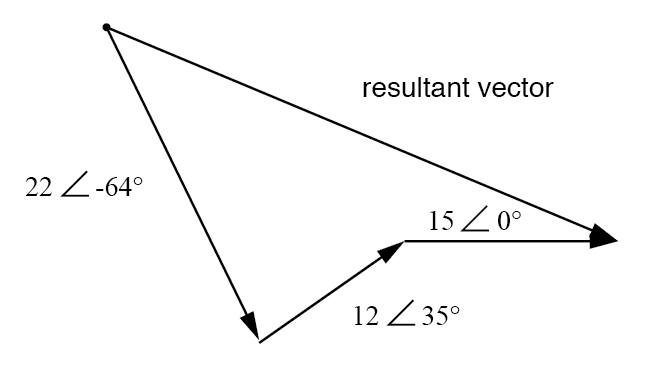
Ergebnis entspricht der Vektorsumme der drei ursprünglichen Spannungen.

Um die Größe und den Winkel des resultierenden Vektors zu bestimmen, ohne auf grafische Bilder zurückgreifen zu müssen, können wir jede dieser komplexen Zahlen in Polarform in eine rechteckige Form umwandeln und addieren.

Denken Sie daran, wir hinzufügen diese Zahlen zusammen, weil die Polaritätsmarkierungen für die drei Spannungsquellen additiv ausgerichtet sind:

In Polarform entspricht dies 36,8052 Volt ∠ -20,5018°. Konkret bedeutet dies, dass die an diesen drei Spannungsquellen gemessene Spannung 36,8052 Volt beträgt und den 15 Volt (0° Phasenreferenz) um 20,5018° nacheilt.

Ein an diesen Punkten angeschlossenes Voltmeter in einem realen Stromkreis würde nur die polare Größe der Spannung (36,8052 Volt) anzeigen, nicht den Winkel. Ein Oszilloskop könnte verwendet werden, um zwei Spannungswellenformen anzuzeigen und somit eine Phasenverschiebungsmessung bereitzustellen, aber kein Voltmeter.

Das gleiche Prinzip gilt für Wechselstrom-Amperemeter:Sie zeigen die polare Größe des Stroms an, nicht den Phasenwinkel.

Dies ist äußerst wichtig, um berechnete Spannungs- und Stromwerte mit realen Stromkreisen in Beziehung zu setzen.

Obwohl die rechteckige Schreibweise für Addition und Subtraktion praktisch ist und tatsächlich der letzte Schritt in unserem Beispielproblem hier war, ist sie für praktische Messungen nicht sehr anwendbar.

Rechteckige Figuren müssen in Polarfiguren umgewandelt werden (insbesondere polare Größe ) bevor sie mit tatsächlichen Stromkreismessungen in Verbindung gebracht werden können.

Wir können SPICE verwenden, um die Genauigkeit unserer Ergebnisse zu überprüfen. In dieser Testschaltung ist der Widerstandswert von 10 kΩ ziemlich willkürlich. Es ist da, damit SPICE keinen Leerlauffehler deklariert und die Analyse abbricht.

Auch die Wahl der Frequenzen für die Simulation (60 Hz) ist recht willkürlich, da Widerstände für alle Frequenzen von Wechselspannung und -strom gleichförmig ansprechen. Es gibt andere Komponenten (insbesondere Kondensatoren und Induktivitäten), die nicht gleichmäßig auf unterschiedliche Frequenzen reagieren, aber das ist ein anderes Thema! (Abbildung unten)

Spice-Schaltplan.

v1 1 0 ac 15 0 sin v2 2 1 ac 12 35 sin v3 3 2 ac 22 -64 sin r1 3 0 10k .ac link 1 60 60 Ich verwende eine Frequenz von 60 Hz .print ac v(3,0) vp(3,0) als Standardwert .Ende Frequenz v(3) vp(3) 6.000E+01 3.681E+01 -2.050E+01 

Tatsächlich erhalten wir eine Gesamtspannung von 36,81 Volt ∠ -20,5° (bezogen auf die 15-Volt-Quelle, deren Phasenwinkel willkürlich auf null Grad als „Referenz“-Wellenform angegeben wurde).

Auf den ersten Blick ist dies kontraintuitiv. Wie ist es möglich, bei in Reihe geschalteten 15-Volt-, 12-Volt- und 22-Volt-Versorgungen eine Gesamtspannung von knapp über 36 Volt zu erreichen? Bei Gleichstrom wäre dies unmöglich, da sich die Spannungswerte je nach Polarität entweder direkt addieren oder subtrahieren.

Aber bei Wechselstrom kann unsere „Polarität“ (Phasenverschiebung) überall zwischen Vollunterstützung und Vollentgegensetzung variieren, und dies ermöglicht solch eine paradoxe Summierung.

Was wäre, wenn wir den gleichen Stromkreis nehmen und einen der Anschlüsse der Versorgung vertauschen? Sein Beitrag zur Gesamtspannung wäre dann das Gegenteil von dem, was er vorher war:(Abbildung unten)

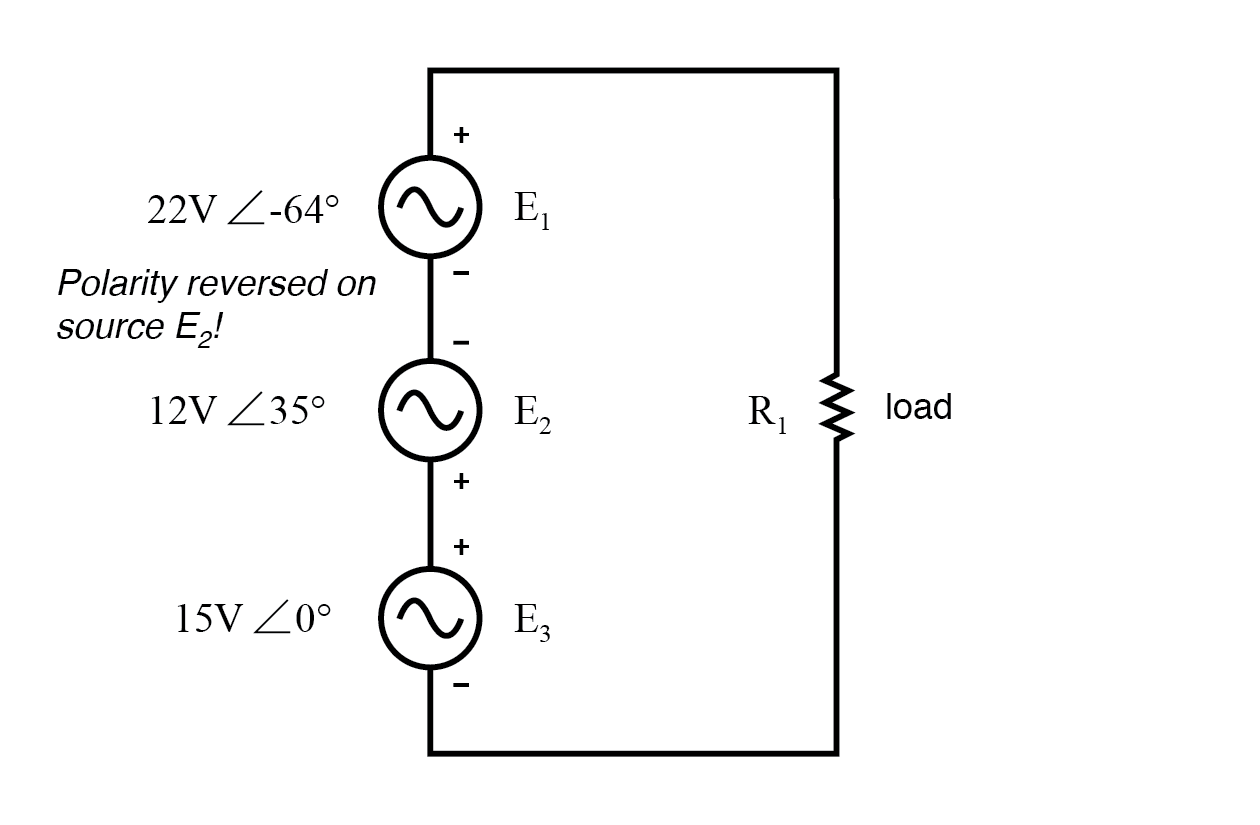
Die Polarität von E₂ (12V) ist umgekehrt.

Beachten Sie, dass der Phasenwinkel der 12-Volt-Versorgung immer noch mit 35° bezeichnet wird, obwohl die Leitungen vertauscht wurden. Denken Sie daran, dass der Phasenwinkel eines Spannungsabfalls in Bezug auf seine angegebene Polarität angegeben wird. Obwohl der Winkel immer noch als 35° angegeben ist, wird der Vektor um 180° entgegengesetzt zu dem gezeichnet, was er vorher war:(Abbildung unten)

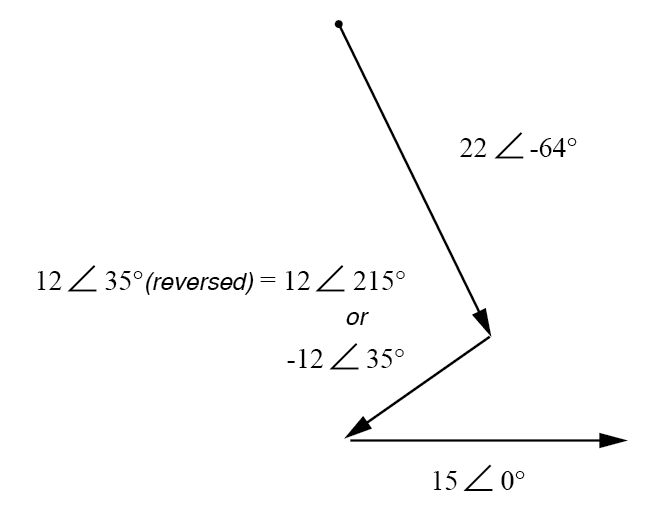
Die Richtung von E₂ ist umgekehrt.

Der resultierende (Summen-)Vektor sollte am oberen linken Punkt (Ursprung des 22-Volt-Vektors) beginnen und an der rechten Pfeilspitze des 15-Volt-Vektors enden:(Abbildung unten)

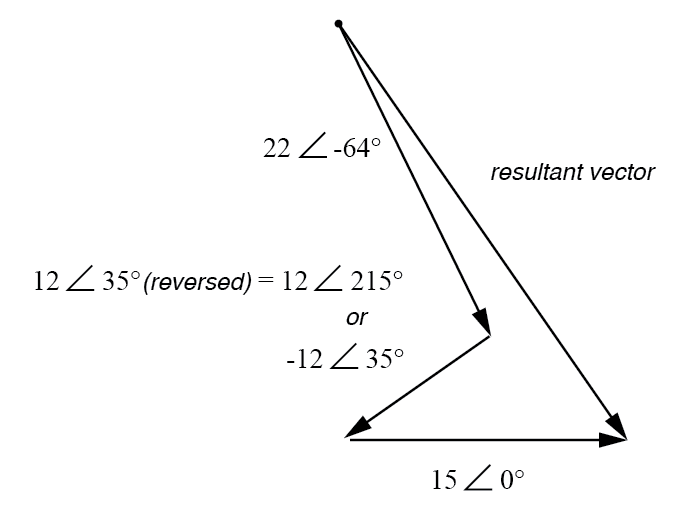
Ergebnis ist die Vektorsumme der Spannungsquellen.

Die Anschlussumkehr an der 12-Volt-Versorgung kann auf zwei verschiedene Arten in Polarform dargestellt werden:durch Addition von 180° zu ihrem Vektorwinkel (also 12 Volt ∠ 215°) oder eine Vorzeichenumkehr der Größe (also - 12 Volt ∠ 35°). In beiden Fällen führt die Umwandlung in eine rechteckige Form zum gleichen Ergebnis:

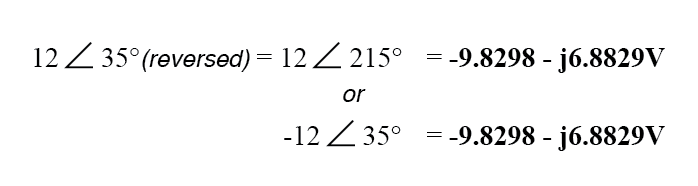
Die resultierende Addition von Spannungen in Rechteckform, dann:

In Polarform entspricht dies 30,4964 V ∠ -60,9368 °. Wir werden wieder SPICE verwenden, um die Ergebnisse unserer Berechnungen zu überprüfen: