Kirchhoffs Strom- und Spannungsgesetz (KCL &KVL) | Beispiel gelöst

KCL &KVL – Kirchhoffs erstes und zweites Gesetz mit gelöstem Beispiel

Ein deutscher Physiker „Robert Kirchhoff“ führte 1847 zwei wichtige elektrische Gesetze ein, mit denen wir leicht den äquivalenten Widerstand eines komplexen Netzwerks und fließender Ströme in verschiedenen Leitern finden können. Sowohl Wechselstrom- als auch Gleichstromkreise können gelöst und vereinfacht werden, indem diese einfachen Gesetze verwendet werden, die als Kirchhoffs Stromgesetz (KCL) und Kirchhoffs Spannungsgesetz (KVL) bekannt sind.

Beachten Sie auch, dass KCL von der Ladungskontinuitätsgleichung im Elektromagnetismus abgeleitet wird, während KVL von der Maxwell-Faraday-Gleichung für statische Magnetfelder abgeleitet wird (die zeitliche Ableitung von B ist 0 ).

Kirchhoff’s Current Law (KCL):

Laut KCL:

In jedem elektrischen Netzwerk ist die algebraische Summe der eingehenden Ströme zu einem Punkt und der ausgehenden Ströme von diesem Punkt Null. Oder die an einem Punkt eintretenden Ströme sind gleich den an diesem Punkt austretenden Strömen.

Mit anderen Worten, die Summe der Ströme, die zu einem Punkt fließen, ist gleich der Summe der Ströme, die von ihm wegfließen. Oder die algebraische Summe der in einen Knoten eintretenden Ströme ist gleich der algebraischen Summe der ihn verlassenden Ströme.

Erklärung von KCL:

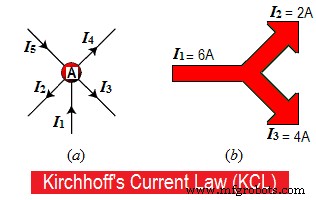
Angenommen, einige Leiter treffen sich an einem Punkt „A“, wie in Abb. 1.a gezeigt. In einigen Leitern fließen Ströme zum Punkt „A“, während in anderen Leitern Ströme von Punkt „A“ abgehen oder abgehen.

Betrachten Sie die eingehenden oder eingehenden Ströme als „positiv (+) in Richtung Punkt „A“, während die ausgehenden oder ausgehenden Ströme von Punkt „A“ „negativ (-)“ sind.
dann:

Ich ₁ + (–Ich ₂ ) + (–Ich ₃ ) + (–Ich ₄ ) + ich ₅ =0

ODER

Ich ₁ + ich ₅ – ich ₂ – ich ₃ – ich ₄ =0

ODER

Ich ₁ + ich ₅ =ich ₂ + ich ₃ + ich ₄ =0

also

Ankommende oder eintretende Strömungen =austretende oder austretende Strömungen

Oder

ΣIch Eingabe =ΣI Verlassen

Beispielsweise nähert sich 8A einem Punkt und 5A plus 3A verlassen diesen Punkt in Abb. 1.b, daher

8A =5A + 3A

8A =8A.

Kirchhoffsches Spannungsgesetz (KVL):

Das zweite Gesetz von Kirchhoff oder KVL besagt, dass;

Mit anderen Worten, in jedem geschlossenen Regelkreis (auch bekannt als Mesh) ist die algebraische Summe der angelegten EMF gleich der algebraischen Summe der Spannungsabfälle in den Elementen . Kirchhoffs zweites Gesetz ist auch als Spannungsgesetz oder Maschengesetz bekannt.

ΣIR=ΣE

Erklärung von KVL:

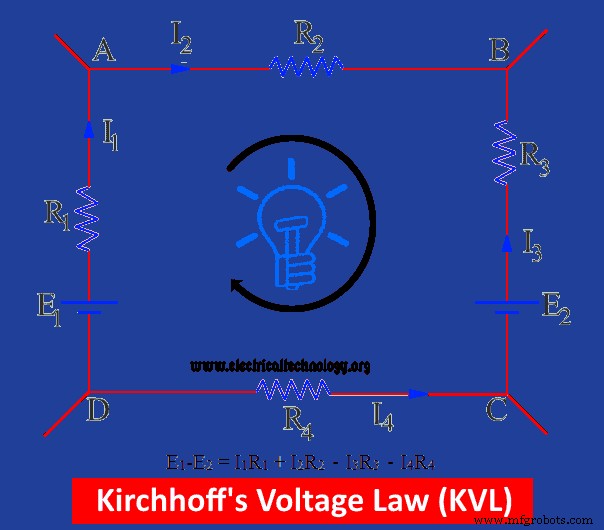
In Abb. ist ein geschlossener Stromkreis dargestellt, der zwei Anschlüsse von Batterien E₁ enthält und E₂ . Die Gesamtsumme der E.M.F’s der Batterien wird durch E₁ angezeigt -E₂ . Die imaginäre Stromrichtung ist ebenfalls in der Abbildung dargestellt.

E₁ treibt den Strom in eine solche Richtung, die positiv sein soll, während E₂ in die Stromrichtung eingreift (d.h. in die entgegengesetzte Richtung der angenommenen Stromrichtung), daher wird es als negativ angenommen. Der Spannungsabfall in diesem geschlossenen Stromkreis hängt vom Produkt aus Spannung und Strom ab.

Der Spannungsabfall in der angenommenen Stromrichtung wird als positiver Spannungsabfall bezeichnet, während der andere als negativer Spannungsabfall bezeichnet wird.

In der obigen Abbildung I₁ R₁ und I₂ R₂ sind positive Spannungsabfälle und I₃ R₃ und I₄ R₄ sind negative V.D.

Wenn wir den geschlossenen Stromkreis (oder jede Masche) umgehen und den Widerstand des Leiters und den darin fließenden Strom multiplizieren, dann ist die Summe der IR gleich Summe der angelegten EMF-Quellen, die an den Stromkreis angeschlossen sind.

Die Gesamtgleichung für die obige Schaltung lautet:

E₁ – E₂ =ich ₁ R₁ + ich ₂ R₂ – ich ₃ R₃ – ich ₄ R₄

Wenn wir in die angenommene Richtung des Stroms gehen, wie in der Abbildung gezeigt, dann wird das Produkt des IR als positiv angenommen, ansonsten negativ.

Gut zu wissen:

Richtung des Stroms:

Es ist sehr wichtig, die Stromrichtung zu bestimmen, wann immer Schaltungen mit den Kirchhoffschen Gesetzen gelöst werden. Dasselbe wie im Fall von Wahlstrom und konventionellem Strom.

Die Stromrichtung kann als Rechts- oder Linkslauf angenommen werden. Sobald Sie die benutzerdefinierte Richtung des Stroms ausgewählt haben, müssen Sie die gleiche Richtung für den gesamten Stromkreis bis zur endgültigen Lösung des Stromkreises anwenden und beibehalten.

Wenn wir den Endwert als positiv erhalten haben, bedeutet dies, dass die angenommene Richtung des Stroms korrekt war. Bei negativen Werten wird die Stromrichtung gegenüber der dann angenommenen umgekehrt.

Schaltungsanalyse nach den Kirchhoffschen Gesetzen

Gelöstes Beispiel für KCL und KVL (Kirchhoffsche Gesetze)

Beispiel:

Widerstände von R₁ =10Ω, R₂ =4Ω und  R₃ =8Ω werden wie abgebildet an zwei Batterien (mit vernachlässigbarem Widerstand) angeschlossen. Finden Sie den Strom durch jeden Widerstand.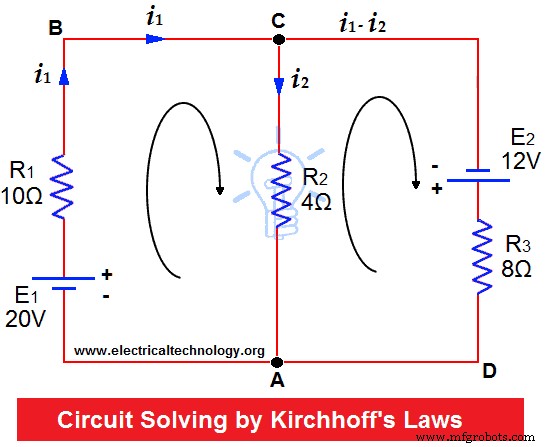

Lösung:

Nehmen Sie an, dass Ströme in die durch Pfeile angezeigte Richtung fließen.

Wenden Sie KCL auf die Kreuzungen C und A an.

Daher Strom im Netz ABC =i ₁

Aktuell in Mesh CA =i ₂

Dann aktuell in Mesh CDA =i ₁ – ich ₂

Nun wenden Sie KVL auf Mesh ABC an, 20V wirken im Uhrzeigersinn. Wenn wir die Summe der IR-Produkte gleichsetzen, erhalten wir:

10i ₁ + 4ich ₂ =20   …   (1)

Im Mesh-ACD wirken 12 Volt im Uhrzeigersinn, dann:

8(i ₁ – ich ₂ ) – 4i ₂ =12

8i ₁ – 8ich ₂ – 4ich ₂ =12

8i ₁ – 12i ₂ =12   …   (2)

Gleichung (1) mit 3 multiplizieren;

30i ₁ + 12i ₂ =60

Auflösen nach i ₁

30i ₁ + 12i ₂ =60

8i ₁ – 12i ₂ =12

___________
38i ₁ =72

Die obige Gleichung kann auch durch Elimination oder Cramers Regel vereinfacht werden.

ich ₁ =72 ÷ 38 =1,895 Ampere =Strom in 10 Ohm Widerstand

Indem wir diesen Wert in (1) einsetzen, erhalten wir:

10 (1,895) + 4i ₂ =20

4i ₂ =20 – 18,95

ich ₂ =0,263 Ampere =Strom in 4-Ohm-Widerständen.

Jetzt

ich ₁ – ich ₂ =1,895 – 0,263 =1,632 Ampere

Anwendungen der Kirchhoffschen Gesetze

• Die Kirchhoffschen Gesetze können verwendet werden, um die Werte unbekannter Größen wie Strom und Spannung sowie die Richtung der fließenden Werte dieser Quintette in der Schaltung zu bestimmen.
• Diese Gesetze können auf jeden Schaltkreis* angewendet werden (siehe die Einschränkung der Kirchhoffschen Gesetze am Ende des Artikels), aber nützlich, um die unbekannten Werte in komplexen Schaltkreisen und Netzwerken zu finden.
• Wird auch in der Knoten- und Maschenanalyse verwendet, um die Werte von Strom und Spannung zu finden.
• Der Strom durch jede unabhängige Schleife wird durch Anlegen von KVL (jeder Schleife) und der Strom in jedem Element eines Stromkreises durch Zählen des gesamten Stroms geführt (anwendbar bei der Schleifenstrommethode).
• Strom durch jeden Zweig wird durch Anwenden von KCL (jeder Verbindung) KVL in jeder Schleife eines Stromkreises geführt (anwendbar bei der Schleifenstrommethode).
• Die Kirchhoffschen Gesetze sind hilfreich, um die Energieübertragung durch einen Stromkreis zu verstehen.

Gut zu wissen:

Diese Faustregeln müssen bei der Vereinfachung und Analyse elektrischer Schaltungen nach den Kirchhoffschen Gesetzen berücksichtigt werden:

• Der Spannungsabfall in einer Schleife aufgrund von Strom im Uhrzeigersinn wird als positiver (+) Spannungsabfall betrachtet.
• Der Spannungsabfall in einer Schleife aufgrund des Stroms gegen den Uhrzeigersinn wird als negativer (-) Spannungsabfall betrachtet.
• Der von der Batterie abgeleitete Strom im Uhrzeigersinn wird als positiv (+) angenommen.
• Der von der Batterie abgeleitete Strom gegen den Uhrzeigersinn wird als positiv (-) angenommen.

Einschränkungen der Kirchhoffschen Gesetze:

• KCL ist unter der Annahme anwendbar, dass Strom nur in Leitern und Drähten fließt. Während in Hochfrequenzschaltungen parasitäre Kapazitäten nicht mehr ignoriert werden können. In solchen Fällen kann Strom in einem offenen Stromkreis fließen, da Leiter oder Drähte in diesen Fällen als Übertragungsleitungen fungieren.
• KVL ist unter der Annahme anwendbar, dass es kein fluktuierendes Magnetfeld gibt, das die geschlossene Schleife verbindet. In Gegenwart eines sich ändernden Magnetfelds in Wechselstromkreisen mit hoher Frequenz, aber kurzer Wellenlänge, ist das elektrische Feld kein konservatives Vektorfeld. Das elektrische Feld kann also nicht der Gradient irgendeines Potentials sein und das Linienintegral des elektrischen Felds um die Schleife herum ist nicht Null, was KVL direkt widerspricht. Deshalb ist KVL in einem solchen Zustand nicht anwendbar.
• Während der Übertragung von Energie vom Magnetfeld zum elektrischen Feld, wo Fudge in KVL eingeführt werden muss, um den P.d (Potenzialunterschied) um den Stromkreis gleich 0 zu machen.

Verwandte Beiträge über Theoreme zur Analyse elektrischer Schaltungen:

• Der Satz von Thevenin. Schritt-für-Schritt-Anleitung mit gelöstem Beispiel
• Theorem von Norton. Einfaches Schritt-für-Schritt-Verfahren mit Beispiel (Bildansichten)
• SUPERNODE Schaltungsanalyse | Schritt für Schritt mit gelöstem Beispiel
• SUPERMESH-Schaltungsanalyse | Schritt für Schritt mit gelöstem Beispiel
• Maximum Power Transfer Theorem for AC &DC Circuits
• Kompensationssatz – Beweis, Erklärung und gelöste Beispiele
• Substitutionssatz – Schritt-für-Schritt-Anleitung mit gelöstem Beispiel
• Theorem von Millman – Analysieren von AC- und DC-Schaltungen – Beispiele
• Überlagerungssatz – Schaltungsanalyse mit gelöstem Beispiel
• Theorem von Tellegen – Gelöste Beispiele &MATLAB-Simulation
• Spannungsteilerregel (VDR) – Gelöste Beispiele für R-, L- und C-Schaltungen
• Current Divider Rule (CDR) – Gelöste Beispiele für AC- und DC-Schaltungen
• Ohmsches Gesetz:Einfache Erklärung mit Aussage und Formeln
• Konvertierung von Stern zu Delta und von Delta zu Stern. Y-Δ-Transformation