home Herstellungstechnologie Produktionsanlagen
Industrielle Fertigung
Industrielles Internet der Dinge | Industrielle Materialien | Gerätewartung und Reparatur | Industrielle Programmierung |
home  MfgRobots >> Industrielle Fertigung >  >> Manufacturing Technology >> Herstellungsprozess

Wellenverzahnungen und -verzahnungen - Dimensionierung und Anwendungen von Keilverzahnungen

Was sind Splines und Serrations?

Wellenverzahnungen und -verzahnungen sind Grate oder zahnartige Keile, die ein integraler Bestandteil der Welle sind und mit Nuten in einer passenden Nabe kämmen, um Drehmoment und Drehbewegung zu übertragen. Beispielsweise könnte ein auf einer Welle montiertes Kegelrad eine männliche Wellenverzahnung verwenden, die mit der weiblichen Verzahnung auf dem Zahnrad übereinstimmt, wie in Abbildung 1 gezeigt.

Obwohl eine Keilwelle so aussieht, als hätte sie eine Reihe von Wellenkeilnuten mit eingedrückten Keilen, sind Keilnuten erheblich stärker als die Keilverbindung, da die Keilnuten die Welle schwächen und ihre Drehmomenttragfähigkeit verringern.

Anwendung von Splines und Zacken

Obwohl sie wie Zahnräder aussehen, werden Splines nur verwendet, um Drehmoment und Rotation auf derselben Achse zu übertragen. Sie werden hauptsächlich aus den folgenden Gründen verwendet.

  1. Mechanische Übertragungselemente wie Zahnräder und Riemenscheiben müssen möglicherweise aufgrund von Design for Manufacturing and Assembly (DFMA), dh während der Montage oder zur Unterstützung der Fertigung, von der Welle entfernt werden.
  2. Eine axiale Relativbewegung des mechanischen Übertragungselements ist für funktionelle Zwecke wie Untersetzungsgetriebe und Kupplungen erforderlich.
  3. Eine hohe Drehmomentübertragung ist erforderlich.

Eine gute Keilverbindung bietet eine sehr sichere Drehmomentübertragung, wenig Spiel, minimales Spiel, gute Zentrierung zwischen den gekoppelten Komponenten, geringe Geräuschentwicklung, geringen Verschleiß und geringe oder keine Axialkräfte.

Oberflächenverschleiß, Reibkorrosion, Zahnbruch und Ermüdungsbruch sind die häufigsten Ausfallarten im Zusammenhang mit Keilwellenverbindungen.

Arten von Splines und Serrations

Der Begriff „Spline“ stellt einen Überbegriff für alle Profile dar und die Splines lassen sich anhand ihrer Flankenform in die folgenden drei Gruppen einteilen.

Keile und Verzahnungen können je nach ihrer relativen axialen Bewegung auch als feste Keile oder flexible Keile gruppiert werden. Fixed Spline ist, wie der Name schon sagt, ein Gelenk, das sich nicht axial bewegt, wie z. B. Zahnräder, Abzieher, Turbinenräder usw.

Flexible Keilwellen gleiten axial, werden hauptsächlich zwischen Wellenkupplungen verwendet und übertragen als feste Keilverbindungen nicht viel Drehmoment.

Parallel-Sided- oder Straight-Sided-Spline

Diese haben gerade und parallele Zahnflanken, wie in der Abbildung unten gezeigt, und gemäß verschiedenen Standards kann die Anzahl der Zähne zwischen 4 und 12 variieren. Sie können aufgrund ihrer großen Zahndicke von klein nach groß ein höheres Drehmoment übertragen als Evolventenkeile und Verzahnungen Durchmesser des Profils. Kann aber aufgrund von Ermüdung aufgrund von Spannungskonzentration im Fuß der Flanken ausfallen.

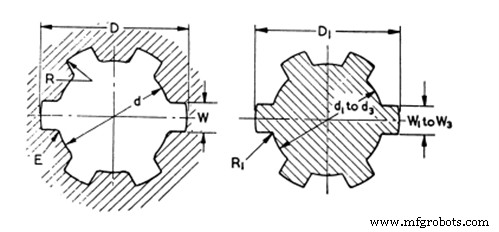
Aufgrund der geraden Flanken fehlt ihm natürlich die Zentrierfähigkeit, wodurch es gezwungen ist, sich auf Passungen mit größerem und kleinerem Durchmesser zu verlassen, um die Zentrierung zu bewältigen. Aufgrund der geraden Schlagfläche entsteht eine Kontaktlinie und ein Oberflächenkontakt wird erst nach einiger Abnutzung bestehen.

Evolvente

Evolventenverzahnungen sind weit verbreitet und den internen und externen Evolventenverzahnungen sehr ähnlich. Sie sind aufgrund des geringeren Spannungskonzentrationsfaktors vergleichbar fester als die parallele Spline und haben eine bessere Oberflächenqualität. Evolventenverzahnungen können durch Zahnradherstellungstechniken hergestellt werden und haben die Fähigkeit, sich unter Last selbst zu zentrieren.

Evolventenverzahnungen werden mit Eingriffswinkeln von 30° hergestellt , 37,5 und 45 o und kann zwischen 60 und 100 Splines gemäß dem American National Standard enthalten. Evolventenverzahnungen können entweder Seitenpassung oder Durchmesserpassung sein.

Zahnungen

Zacken haben auch gerade Flanken, aber sie sind abgewinkelt, wie in der Abbildung unten gezeigt. Der größte Vorteil der Verzahnung besteht darin, dass die Winkelflanken die Wellen und die Nabe zentrieren, was zu einer selbstzentrierenden Verzahnung führt. Flankenwinkel liegen im Allgemeinen zwischen 50° und 90 o .

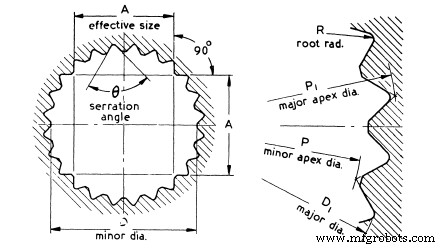
Die Hauptnachteile von Verzahnungen liegen darin, dass sie aufgrund vergleichsweise kleiner Zähne nur für Anwendungen mit niedrigem Drehmoment verwendet werden können. Diese werden nur für die nicht axial bewegte Anwendung verwendet. Wie bei Splines mit geraden Seiten kommt es zu Linienkontakt und Verschleiß.

Berechnung der Spline-Stärke

Bei der Auslegung von Wellenverzahnungen und -verzahnungen müssen die folgenden Belastungen berücksichtigt werden, um die Eignung der Keilverbindungsfestigkeit zu bewerten.

  1. Scherspannung der Keilwelle
  2. Scherspannung der Spline-Zähne
  3. Druckspannung der Keilzähne

Im Allgemeinen wird der Wellendurchmesser durch die Gesamtkonstruktion wie Lageranordnungen, Dichtungen, Elemente usw. vorgegeben.  In diesem Fall können die Berechnungen der Keilwellenfestigkeit auf die folgenden zwei Arten verwendet werden

  1. Die Spannungsberechnung kann verwendet werden, um den Sicherheitsfaktor zu finden, indem die beteiligte Spannung berechnet und mit den zulässigen Spannungen gemäß den Versagensarten verglichen wird.
  2. Anhand des Sicherheitsfaktors kann die Spline-Verbindung über Spline-Länge, Spline-Typ, Anzahl der Splines etc. definiert werden

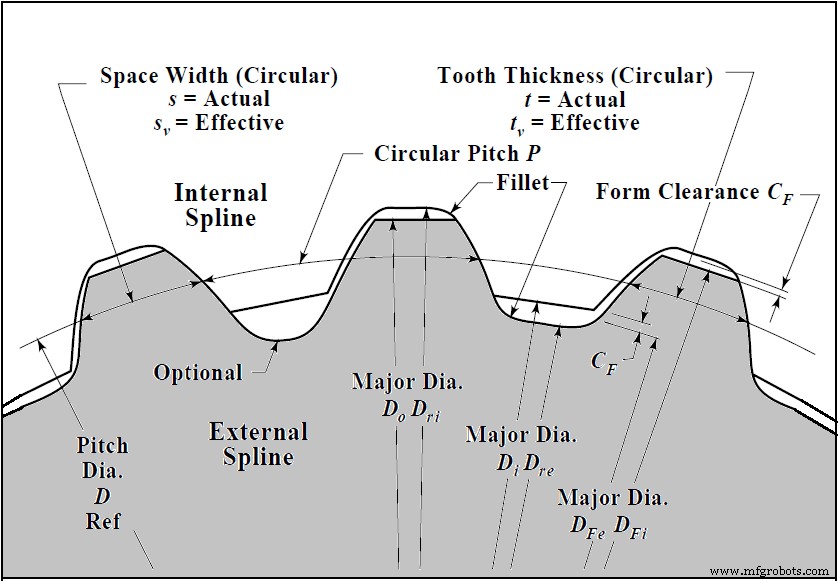
Scherspannung der Keilwelle

Vollwellenspannungen Hohlwellenspannungen
\( S_s =\frac{16T}{\pi{D_{re}}^ {3}} \)  \( S_s =\frac{16T{D_{re}}}{\pi ({D_{re}}^4-D_h^4)} \)
Wo
\(S_s\)   Scherspannung
\({D_{re}}\)   Durchmesser des Splines
\(T\)   Drehmoment
\({D_{h}}\)   Bohrungsdurchmesser der Hohlwelle
[Tabelle „“ nicht gefunden /]

Die mit den obigen Gleichungen berechnete Spannung darf die zulässige Spannung (\(S^a\)) des Spline-Materials nicht überschreiten und kann wie folgt angezeigt werden

\(S^a_s \geq S_s \frac{{K_{a}}}{{L_{f}}}\)

Normalerweise wird der Sicherheitsfaktor unter Verwendung der zulässigen Spannung für verschiedene Materialien unter Verwendung der folgenden Gleichungen berechnet

Zulässige Wellenbelastung
\(S^a_s ={N_{sf}}S_s \frac{{K_{ a}}}{{L_{f}}}\) \(S^a_s \geq S_s \frac{{K_{a}}}{{L_{f}}}\)
Wo
\(S_s\)   Scherspannung
\(S^a_{s}\)   Zulässige Scherspannung
\(T\)   Drehmoment
\({L_{f}}\)   Lebensfaktor
\({N_{sf}}\)   Sicherheitsfaktor
\({K_{a}}\)   Anwendungsfaktor

Scherspannung der Spline-Zähne

Scherspannung in Keilzähnen
\(S_s =\frac{4T{K_{m}} }{DN{F_{e}}{t_{e}}}\) 
\(S_s\)   Induzierte Scherspannung in Stacheln
\(D\)   Teilungsdurchmesser
\(T\)   Drehmoment
\({K_{m}}\)   Lastverteilungsfaktor
\({F_{e}}\)   Effektive Gesichtsbreite
\({t_{e}}\)   Sehnendicke an der Tonhöhe (ungefähr gleich D/2N)
\(N\)   Anzahl der Spline-Zähne

Druckspannung der Spline-Zähne

Druckspannung an Keilzähnen
\( S_c =\frac{2T{K_{m}} }{DN{F_{e}h}} \) 
\(S_c\)   Druckspannung
\({K_{m}}\)   Lastverteilungsfaktor
\(T\)   Drehmoment
\({F_{e}}\)   Effektive Gesichtsbreite
\(h\)   Radiale Höhe des Kontaktzahns

Ähnlich wie bei Scherspannungen sollten berechnete Druckspannungen mit zulässigen Druckspannungen verglichen werden und dürfen diese nicht überschreiten, um ein Versagen zu vermeiden.

\(S^a_s \geq S_s \frac{{K_{a}}}{{L_{f}}}\) – Flexible Splines

\(S^a_s \geq S_s \frac{{K_{a}}}{{L_{f}}}\) – Feste Splines

Zulässige Wellenbelastung
Flexible Splines Feste Splines
\(S^a_c ={N_{sf}}S_c \frac{{K_{a}}}{{L_{w} }}\) \(S^a_c ={N_{sf}}S_c \frac{{K_{a}}}{{9L_{f}}}\)
Wo
\(S_s\) Scherspannung
\({S^a_{s}}\) Zulässige Scherspannung
\(T\) Drehmoment
\({L_{f}}\) Lebensfaktor
\({N_{sf}}\)  Sicherheitsfaktor
\({K_{a}}\)  Anwendungsfaktor

Spline-Stressfaktoren

Zulässiger Stress

Das Verhältnis zwischen zulässiger Spannung und spezifizierter Mindeststreckgrenze gemäß dem AISC-Code.

Zulässige Spannungen vs. Streckgrenze
Zulässige Zugspannung \({0.45}S_{y}\leq S^a_{t}\leq {0.6}S_{y}\)
Zulässige Scherspannung (\({S^a_{s}}\)) \(S^a_{s}=0,4S_{y }\)
Zulässige Druck-/Lagerspannung (\({S^a_{c}}\)) \(0.45S_{y}\leq S^a_{c} \leq 0.6S_{y}\)
Zulässige Biegespannung (\({S^a{b}}\)) \(0.6S_{y} \leq S^a_{b} \leq 0.75S_{y} \)
Wo
\({S_{y}}\) Streckgrenze des Materials

Lastverteilungsfaktor für Splines Km

Die Last wird gleichmäßig verteilt, wenn die übertragende Last eine reine radiale Torsion ist und die Torsionsradiallast in der Mitte der Keilwellenlänge liegt. Aber wenn zum Beispiel ein Kegelrad verwendet wird, bringt dies einige unerwünschte axiale Belastungen in die Verzahnung ein.

Eine Fehlausrichtung von Keilkupplungen wurde als schädlich für Keile erkannt, da sie eine erhebliche Belastungskonzentration auf Keilzähne verursacht und den Verschleiß und die Reibermüdung von Keilen beschleunigt.

Lastverteilungsfaktor für Splines Km
Effektive Breite (Fe)
Fehlausrichtung ½ Zoll. (12,7 mm) 1 Zoll. (25,4 mm) 2 Zoll. (50,8 mm) 4 Zoll. (101.6)
0,001 Zoll / Zoll
(mm/mm)		 1 1 1 1 ½
0,002 Zoll / Zoll
(mm/mm)		 1 1 1 ½ 2
0,004 Zoll / Zoll
(mm/mm)		 1 1 ½ 2 2 ½
0,008 Zoll / Zoll
(mm/mm)		 1 ½ 2 2 ½ 3

Die folgenden zwei Artikel diskutieren den Lastverteilungsfaktor und wie er die Lebensdauer der Keilverbindung beeinflussen kann.

Lebensdauerfaktor für Splines- Lf

Anzahl der Drehmomentzyklen Ermüdungslebensfaktor, Lf
Unidirektional Vollständig - umgekehrt
1.000 1.8 1.8
10.000 1.0 1.0
100.000 0,5 0,4
1.000.000 0,4 0,3
10.000.000 0,3 0,2

Spline-Anwendungsfaktor – Ka

Wenn auf das verbundene Element axiale oder radiale Stoßbelastungen einwirken, sollte darauf geachtet werden, die äußeren axialen und radialen Stoßbelastungen abzustützen, um die Lebensdauer der Verbindung zu verlängern. Dies sollte auch bei den Berechnungen mit dem Spline-Anwendungsfaktor berücksichtigt werden .

Der Anwendungsfaktor kompensiert alle Unsicherheiten bei Belastungen und Stößen, wobei, wenn alles glatt und gleichmäßig ist, Ka gleich 1 ist.

Eingangsquellenkategorie
(Antriebseingang oder -maschine)		 Art der Belastung
Einheitlich Leichte Erschütterung Intermittierender Schock schwerer Schock
Generatoren, Ventilatoren Oszillierende Pumpen Aktuatoren Pressen, Scheren
Uniform (Turbine, Motor) 1 1.2 1,5 1.8
leichter Schock, (Hydraulikmotor) 1.2 1.3 1.8 2.1
Mittlerer Schock, (Verbrennungsmotor 2 2.2 2.4 2.8

Tabelle 1 Spline-Anwendungsfaktor (Ka)

Lebensdauerfaktor für Splines Lw

Lebensdauerfaktoren für Keile unter Verschleißbedingungen basieren auf der Anzahl der Umdrehungen der Keilverbindung, nicht auf reversiblen Zyklen. Der Verschleißlebensdauerfaktor gilt nur für Berechnungen der Druckspannung von flexiblen oder gleitenden Splines, da jedes Mal, wenn die Splines hin und her gleiten, die Zähne abgenutzt werden.

Anzahl der Umdrehungen des Splines Lebensdauerfaktor für Verzahnungen (Lw )
10.000 4
100.000 2.8
1.000.000 2
10.000.000 1.4
100.000.000 1
1.000.000.000 0,7
10.000.000.000 0,5

#Produktdesigntipp Ein fester Spline kann 9-mal mehr Druckspannungen aufnehmen als ein flexibler Spline

Standards


Herstellungsprozess

  • Herstellungsprozess
  • 3d Drucken
  • Automatisierungssteuerung System
  • Industrietechnik
    1. Roll Pin Punches:Verwendung und Anwendungen
    2. Unterschiede und Anwendungen von Senkerodieren und Drahterodieren
    3. Industriepumpen-Kategorien:Einführung und Anwendungen
    4. Frässpindel und die bemerkenswerten Anwendungen
    5. Hartmetallwerkzeuge und Hartmetallhalter - Vorteile und Anwendungen
    6. 9 Arten von Gewindeschneidwerkzeugen und die Anwendungen
    7. Verschiedene Arten von Druckguss und ihre Anwendungen
    8. Anwendungen, Vor- und Nachteile des WIG-Schweißens
    9. Anwendungen, Vor- und Nachteile des UP-Schweißens
    10. Anwendungen, Vor- und Nachteile des Plasmalichtbogenschweißens