Theoretische Studie zur Trägermobilität von hydriertem Graphen/hexagonalem Bornitrid-Heterobilayer

Einführung

Hydriertes Graphen (HG) [1, 2] ist eines der vielversprechendsten Materialien auf Graphenbasis. Es hat aufgrund seiner umfangreichen Anwendungen, wie Wasserstoffspeicherung [3], Ferromagnetismus [4], Fluoreszenz [5] und thermische Gleichrichtung [6], breite Aufmerksamkeit erregt. Im Gegensatz zu metallischem Graphen ist HG der Halbleiter mit einer einstellbaren Bandlücke [7, 8]. Somit kann es als Kanalmaterial von Feldeffekttransistoren (FET) verwendet werden [9]. Ausgezeichnete FETs sollten eine ultrahohe Ladungsträgerbeweglichkeit des Kanalmaterials aufweisen. Bekanntlich ist das traditionelle SiO₂ Substrat hat einen signifikant negativen Einfluss auf die FET-Leistung [10]. Kürzlich haben die Studien gezeigt, dass einschichtiges hexagonales Bornitrid (h-BN) [11, 12] ein vielversprechender Kandidat für das Substrat von Graphen-basierten FETs ist. Monolayer h-BN und HG sind gitterangepasste Strukturen, was auf eine bessere Kontaktleistung hinweist. Daher ist die HG/h-BN-Heterodoppelschicht eine ideale Struktur des FET-Kanals. Leider gibt es nur wenige verwandte Studien zu den elektronischen Eigenschaften der HG/h-BN-Heterodoppelschichtstruktur. Die Trägermobilitätsleistung der HG/h-BN-Heterodoppelschicht ist noch eine offene Frage.

Die meisten aktuellen Studien zu HG widmen sich der Entwicklung der gewünschten elektronischen Eigenschaften durch Hydrierung [13,14,15,16,17,18]. Gaoet al. [13] untersuchten die Wasserstoffbedeckung und die Konfigurationsabhängigkeit der Bandlücke von HG. Sahinet al. [14] verglichen die Wirkung von Graphen-Nanomaschen mit Adatom-Muster (Hydrierung) und mit Lochmuster (Entfernung von Kohlenstoffatomen) auf die Bandstruktur. Shkrebtii et al. [15] untersuchten die Bandstruktur von HG, wobei die Struktur von HG in C₁₆ . begrenzt ist H_n System (n = 0,2,8,16). Songet al. [16] berechneten die Bandlücke von HGs mit unterschiedlichen Hexagon-Leerstellen. Bruzzoneet al. [17] berechneten die Mobilitäten von HG mit unterschiedlicher Wasserstoffbedeckung (100%, 75%, 25%) durch Ab-initio-Simulationen und fanden heraus, dass 25% HG die höchste Mobilität aufweisen. Es gibt auch einige Studien zur Anwendung der Hydrierung in h-BN. Chenet al. [19] nutzten die Hydrierung, um einen Übergang von Halbleiter zu Metall in h-BN zu realisieren. Lianget al. [20] untersuchten die Wechselwirkungen zwischen 100 % HG und 100 % hydriertem h-BN. Es zeigt, dass die Elektronenmobilität von HG/hydriertem h-BN nur 50 cm ² . beträgt /(V s), was weit von dem von Graphen entfernt ist.

Kurz gesagt, die aktuellen Studien zur Trägermobilität der HG/h-BN-Heterodoppelschicht reichen noch nicht aus. Die Hauptfaktoren, die die Trägermobilität der HG/h-BN-Heterodoppelschicht beeinflussen, nämlich Wasserstoffbedeckung, Hydrierungsmuster und das Stapelmuster zwischen HG und h-BN, sollten geklärt werden. In dieser Arbeit wurden die Trägermobilitäten von HG/h-BN-Heterodoppelschichtstrukturen basierend auf den First-Principles-Rechnungen untersucht. Zunächst wurde die Wirkung des h-BN-Substrats auf die Mobilitäten von HG untersucht. Zweitens wurden die elektronischen Eigenschaften von HG mit unterschiedlicher Wasserstoffbedeckung verglichen. Schließlich wurden verschiedene Hydrierungsmuster bei 25 % und 6,25 % HG angewendet, um den Einfluss des Hydrierungsmusters aufzuzeigen.

Methoden

Alle Berechnungen wurden in Atomistix ToolKit (ATK) [21] basierend auf der Dichtefunktionaltheorie (DFT) implementiert. Die Austauschkorrelation ist die generalisierte Gradienten-Approximation (GGA) mit dem Perdew-Burke-Ernzerhof (PBE)-Funktional. Die Van-der-Waals-Korrektur (vdW) verwendet die Grimme DFT-D2-Methode [22] für die Heterodoppelschichtstrukturen. Die Zellenlänge in z Richtung (senkrecht zur HG-Ebene) beträgt 20 Å, um den Effekt der periodischen Bilder zu eliminieren. Die k-Punkt-Abtastung beträgt 33 × 33 × 1 Monkhorst-Pack-Gitter.

Die Methode der Deformationspotential-Approximation (DPA) [23] wird verwendet, um die Trägermobilität zu untersuchen; der Ausdruck der Trägermobilität von 2D-Material [24, 25] ist:

wo e ist die Elektronenladung, ћ ist die reduzierte Planck-Konstante, k _B ist Boltzmann-Konstante, T ist die Temperatur (in den Fällen ist sie auf 300 K eingestellt) und C _2D ist der Elastizitätsmodul der Ausbreitungsrichtung. E ₁ ist die Deformationspotentialkonstante definiert durch E ₁ = ΔV /(Δl /l ₀ ). V ist die Energieänderung bei richtiger Zellkompression und -dilatation. Für Elektronen wird die Änderung des Leitungsbandminimums (CBM) und für Löcher das Valenzbandmaximum (VBM) verwendet. l ₀ ist die Gitterlänge in Transportrichtung und Δl ist seine Verformung (Δl /l ₀ auf –  0,01, –  0,005, 0, 0,005, 0,01) eingestellt ist). m ^* ist die effektive Masse in Transportrichtung, berechnet nach:

wo k ist der Wellenvektor und E ist die Energie. m _d ist die äquivalente Zustandsdichte, definiert als m _d = (m _x m _y ) ^0,5 . Die Deformationspotentialkonstante und die effektive Masse können aus Bandstrukturen abgeleitet werden, während der Elastizitätsmodul aus den Phononendispersionsbeziehungen gewonnen wird. Es sollte betont werden, dass die DPA-Methode die Beweglichkeiten von Arsenen, Antimonen [26] und Silicen [27] überschätzen kann, da sie die Wirkung von biegeakustischen (ZA) Phononen nicht berücksichtigt. Shuaiet al. [28, 29] diskutierten die Anwendbarkeit von DPA und fanden heraus, dass damit die elektronischen Eigenschaften von Graphen und Graphin gut abgeschätzt werden können. Die ZA-Phononen spielen eine untergeordnete Rolle bei Elektron-Phonon-Wechselwirkungen für zweidimensionale Kohlenstoffmaterialien. Die elektronische Mobilität von Graphen [28] bei Raumtemperatur wird auf 3,4 × 10 ⁵ . geschätzt cm ² /(V s) nach DPA-Methode und 3.2 × 10 ⁵ cm ² /(V s) [28] unter Berücksichtigung aller Elektron-Phonon-Wechselwirkungen. Was HG betrifft, werden wir die Wirkung von ZA-Phononen im nächsten Teil erneut analysieren.

Ergebnisse und Diskussion

Zunächst wurden verschiedene Stapelmuster zwischen h-BN und HG untersucht, wobei das HG zu 100 % hydriert ist. Es sollte betont werden, dass die Wechselwirkung zwischen HG und h-BN eine vdW-Kraft ist, die viel schwächer ist als die kovalente Bindung. Daher ist es unnötig, die anderen HG/h-BN-Heterodoppelschichten zu analysieren. Es gibt vier mögliche Stapelmuster für die Heterodoppelschicht, wie in Abb. 1a–d zu sehen, wobei „a ” ist ein Gitterparameter und “d “ ist der Zwischenschichtabstand. Der Zwischenschichtabstand ist definiert als der Abstand zwischen den geometrischen Zentren der HG-Schicht und der h-BN-Schicht, wie in Fig. 1a markiert. In den Mustern I und II befinden sich die beiden Skelette in AA-Stapelung, während sich in den Mustern III und IV in AB-Stapelung befinden. Die Strukturen wurden zunächst mit der LBFGS-Optimierermethode geometrieoptimiert. Die Konvergenzkriterien für die Krafttoleranz liegen unter 0,001 eV/Å. Nach der Geometrieoptimierung beträgt der Elementarzellenparameter für alle Stapelmuster 2,52 Å, während der Zwischenschichtabstand vom Stapelmuster abhängt. Der Zwischenschichtabstand von Muster I ist am niedrigsten und Muster III ist am höchsten. Die vdW-Korrekturen der vier Muster betragen – 651,69 meV, – 658.14 meV, – 658.22 meV bzw. – 651,54 meV. Offensichtlich stimmt die Tendenz der vdW-Wechselwirkung mit der des Zwischenschichtabstands überein.

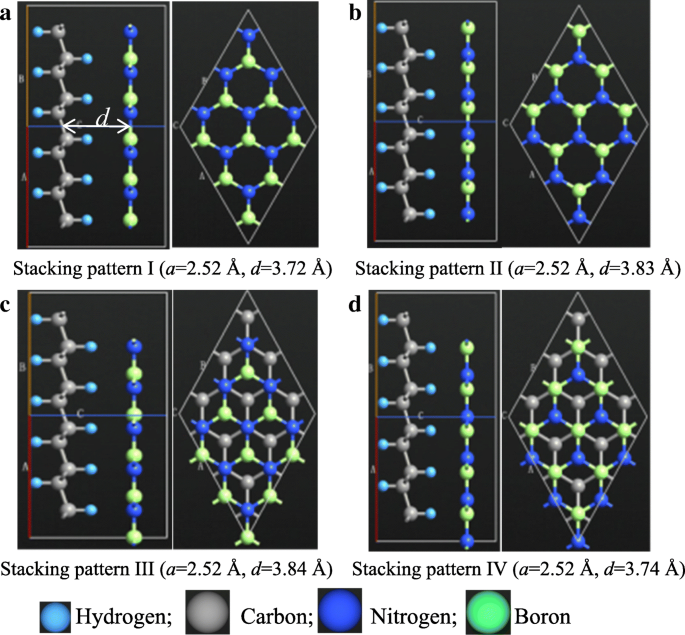
a –d Mögliche Stapelmuster der 100 %-HG/h-BN-Heterodoppelschicht

Die Bandstruktur ist eine der wichtigsten elektronischen Eigenschaften. Die entsprechenden Bandstrukturen der Stapelmuster I–IV sind in Abb. 2 dargestellt. Die beiden fetten Linien in jeder Figur stellen die Bänder dar, einschließlich CBM (nach oben) bzw. VBM (nach unten). Γ (0,0,0), M (0,0.5,0), K (0.333,0.333,0) sind die Symmetriepunkte in der Brillouin-Zone. Die wichtigsten Bandstrukturinformationen, einschließlich der direkten Bandlücke (DBG), der indirekten Bandlücke (IBG), der CBM- und VBM-Positionen, sollten beachtet werden. Im Allgemeinen haben die vier Muster ähnliche Bandstrukturen. Für die Muster I–IV befinden sich CBM und VBM jeweils am Punkt K und Γ. Muster I und IV haben ähnliche DBG (4,35 eV) und IBG (3,25 eV), während DBG und IBG der Muster II und III etwa 4,22 eV und 2,98 eV betragen. Durch den Vergleich ihres Zwischenschichtabstands kann geschlossen werden, dass die stärkere Wechselwirkung zwischen den Schichten zu einer größeren Bandlücke führt. Es sollte betont werden, dass die Bandstruktur von einlagigem h-BN auch mit PBE berechnet wird. Die Bandlücke von h-BN beträgt 4,65 eV, was gut mit dem in [30] angegebenen Wert übereinstimmt. Insgesamt ist die Methode für h-BN geeignet.

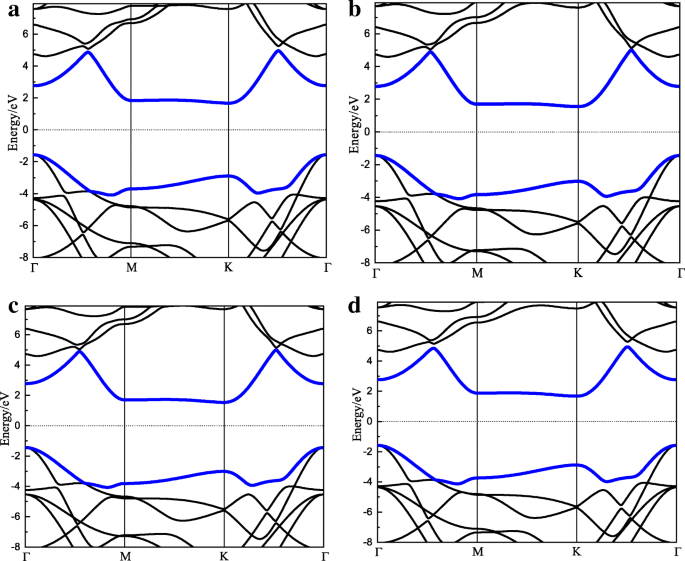
a –d Die Bandstrukturen der 100 %-HG/h-BN-Heterodoppelschicht-Stapelmuster I–IV

Zweitens werden die Einflüsse der Wasserstoffbedeckung und des Hydrierungsmusters betrachtet, während der Einfluss der Hydrierung von der Änderung kovalenter Bindungen herrührt, die viel stärker ist als die vdW-Kraft. Daher wird in diesem Teil nur die HG-Monoschicht untersucht. Die betrachteten Strukturen sind in Abb. 3 dargestellt, wobei „ " und " ”bezeichnet die Kohlenstoffatome, die an verschiedenen Seiten mit Wasserstoffatomen verbunden sind. Aus Gründen der Stabilität der Gesamtstruktur sind Wasserstoffatome gleichmäßig auf jeder Seite verteilt. Für 100 % HG hat es nur ein stabiles Muster. Fünfundzwanzig Prozent HG, zusammengesetzt aus 8C und 2H, haben drei verschiedene Muster. Für 6,25% HG hat es 32C und 2H in der primitiven Zelle. Es werden nur zwei Muster von 6,25% HG berücksichtigt. Wie in Fig. 3b, c gezeigt, sind zwei hydrierte Kohlenstoffatome in Muster I aneinander angrenzend und in Muster II voneinander entfernt. Es sollte beachtet werden, dass 6,25 % Muster I, 25 % Muster I und 100 % HG vom gleichen Typ sind (zwei hydrierte Kohlenstoffatome sind benachbart). In Abb. 3, E _f ist die Bildungsenergie pro Atom

wo E _Gesamt ist die Gesamtenergie von HG, E _Graphen bezieht sich auf die Energie von reinem Graphen, E _H ist die Energie pro Atom des H₂ Molekül und n _H ist die Zahl der adsorbierten Wasserstoffatome. E _f wird verwendet, um die Stabilität der Struktur zu überprüfen, und das negative E _f weist auf thermodynamische Stabilität hin. Die Ergebnisse in Abb. 3 implizieren, dass alle aufgeführten HGs stabil sind. η bezeichnet den prozentualen Anstieg des Gitterparameters von HG im Gegensatz zu Graphen (die minimale Elementarzellenlänge von Graphen beträgt 2,47 Å). Insgesamt nimmt die Gitterverstärkung mit abnehmender Wasserstoffbedeckung ab. Für 6,25% HG, η ist fast vernachlässigbar. Neben der Wasserstoffbedeckung beeinflusst auch das Hydrierungsmuster das Gitter. Für 25% HG ist Muster I von den drei Mustern am wenigsten vergrößert, hauptsächlich weil die hydrierten Kohlenstoffatome benachbart sind. Δ ist der Knickparameter, der als Standardabweichung der Verschiebungen der Kohlenstoffatome außerhalb der Ebene definiert ist. Im Allgemeinen nimmt der Knickparameter mit zunehmender Wasserstoffbedeckung zu.

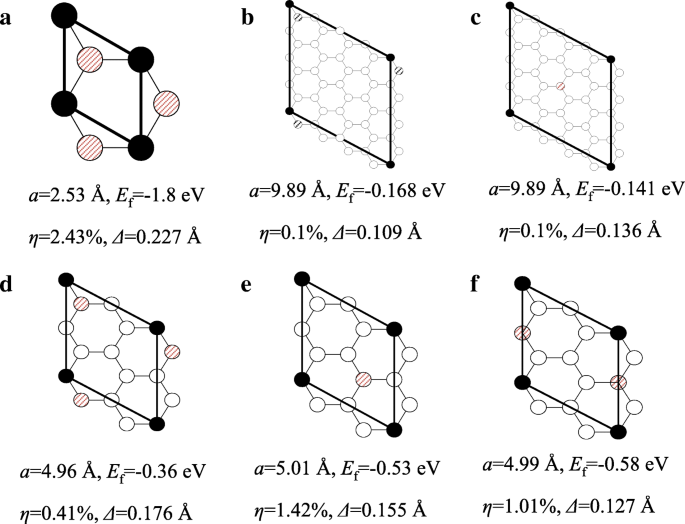
Schema einer primitiven Zelle von HGs mit unterschiedlicher Wasserstoffbedeckung und Muster. a 100%. b , c 6,25% Muster I und II. d , f 25 % Muster I–III

Die Bandstrukturen der obigen HGs sind in Abb. 4 dargestellt. Die Bandlücke von 100 % HG beträgt etwa 4,14 eV, in guter Übereinstimmung mit der bisherigen Literatur [16, 31]. Bei 25 % HG wird die Bandlücke stark durch das Hydrierungsmuster beeinflusst. Muster II hat einen IBG von 3,0 eV, während der IBG von Muster III 0 eV beträgt. Der IBG von null auf ungleich null zeigt einen Übergang von metallisch zu Halbleiter an. Darüber hinaus weist Muster II unterschiedliche DBG und IBG auf, was darauf hindeutet, dass sich seine CBM und VBM an unterschiedlichen Punkten befinden. Für 6,25% HG liegen VBM und CBM für beide der beiden Muster an den gleichen Punkten, wobei Muster I (0,153, 0,423, 0) und Muster II (0,24, 0,24, 0) ist. Die Bandlücke von zwei 6,25 % HG beträgt 0 eV und 0,49 eV, die beide im Gegensatz zu 100 % HG deutlich reduziert sind. Im Allgemeinen sind sowohl die Wasserstoffbedeckung als auch die Hydrierungsmuster wirksame Methoden, um die Bandlücke zu modulieren.

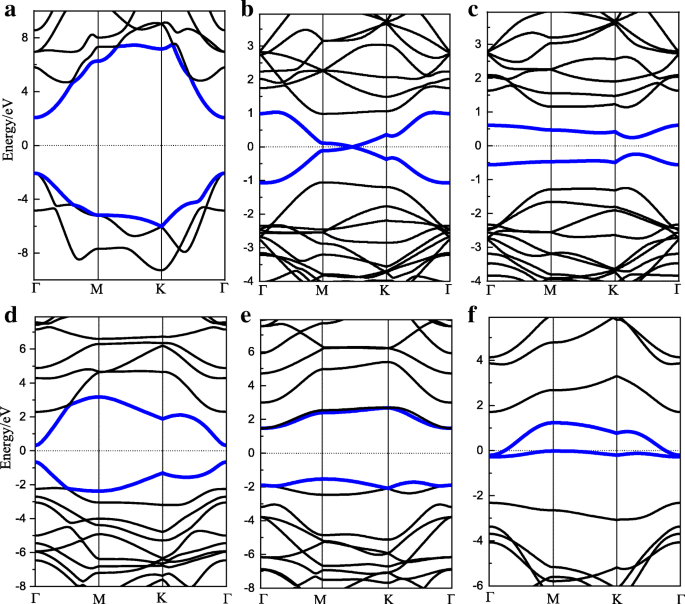
Bandstrukturen von HGs. a 100%. b , c 6,25% Muster I und II. d , f 25 % Muster I–III

Tabelle 1 zeigt die geschätzten Werte des Elastizitätsmoduls C _2D , effektive Masse m ^* und Verformungspotentialkonstante E ₁ . C _2D und m ^* sind richtungsabhängige Parameter. Von allen Richtungen sind ΓM und ΓK am meisten betroffen. Daher C _2D (ΓM/ΓK) und m * (ΓM/ΓK) sind in Tabelle 1 aufgeführt. C _2D = ρv _g ² , wobei ρ ist die Dichte und v _g bezeichnet die Gruppengeschwindigkeit des akustischen Phonons. Da die Hydrierung nur wenige Auswirkungen auf die Gruppengeschwindigkeit hat, ist C _2D verschiedener HGs sind einander ähnlich. Die HG v _g beträgt etwa 23 km/s in K-Richtung und 19,4 km/s in ΓM, also C _2D (ΓK) ist viel höher als C _2D (ΓM). Die Verformungspotentialkonstante weist bei den verschiedenen Mustern keine regelmäßige Tendenz auf. Im Allgemeinen erhöht die vdW-Wechselwirkung zwischen HG und h-BN die Deformationspotentialkonstante.

Die effektive Masse ist komplizierter, da sie von Träger und Richtung abhängt. Bei der effektiven Masse sind drei Punkte zu beachten. Erstens sind die effektive Elektronenmasse von 100 % HG und 100 %-HG/h-BN-Heterodoppelschicht isotrop, d. h. m *(ΓM) = m *(ΓK). Die Heterodoppelschichtstruktur führt zu einem leichten Abfall der effektiven Elektronenmasse im Vergleich zu 100 % HG-Monoschicht. Das Stapelmuster hat einen geringen Einfluss auf die effektive Elektronenmasse (alle vier Stapelmuster sind ungefähr 0,90). Zweitens, unter dem gleichen Hydrierungsmuster (d. h. 100 %, 25 % Muster I und 6,25 % Muster I) ist das Elektron m *(ΓK) nimmt mit der verringerten Wasserstoffbedeckung ab. Es wird gezeigt, dass die Grenze 0,024 (die effektive Masse von Graphen) beträgt, wenn die Wasserstoffbedeckung auf Null sinkt. Drittens wird die effektive Masse bei derselben Wasserstoffbedeckung auch durch das Hydrierungsmuster beeinflusst. Für 25% HG ist die effektive Elektronenmasse des Musters I viel geringer als die der anderen beiden. Kurz gesagt, es ist wahrscheinlicher, dass die effektive Masse durch Hydrierung beeinflusst wird, nicht jedoch der Elastizitätsmodul und die Verformungspotentialkonstante.

In Tabelle 2 werden die Elektronen- und Lochmobilitäten basierend auf den obigen Parametern berechnet. Da die effektive Masse eher betroffen ist, ist die Mobilitätstendenz ähnlich der der effektiven Masse. Im Allgemeinen verringert die Hydrierung die Mobilität von Graphen dramatisch. Die theoretische Mobilität von Graphen (3,2 × 10 ⁵ cm ² /(V s)[28]) ist mehrere Größenordnungen höher als die von HG. Darüber hinaus haben HGs asymmetrische (μ_e ≠ μ_h ) und anisotrop (μ (ΓM) ≠ μ (ΓK)) Mobilitäten. Es gibt drei Details, die beachtet werden sollten. Erstens nimmt bei demselben Hydrierungsmuster die Elektronenmobilität mit zunehmender Wasserstoffbedeckung monoton ab. Wenn jedoch ein anderes Hydrierungsmuster verwendet wird, ist die Schlussfolgerung nicht immer bestätigt. Beispielsweise sind die Beweglichkeiten von 25 % Muster II niedriger als die von 100 % HG. Zweitens hat Muster I für 25 % und 6,25 % HG einen höheren μ _e im Vergleich zu den anderen Mustern. Die μ _e (ΓK) von 25 % Muster I ist 8985,85 cm ² /(V s) und von 6,25% Muster I ist 23.470,98 cm ² /(V s), viel höher als schwarzes Phosphoren [24] und MoS₂ [32]. Drittens beeinflusst das h-BN-Substrat die Lochmobilitäten signifikant, während es nur geringe Auswirkungen auf die Elektronenmobilitäten hat. Dies zeigt an, dass die Lochbeweglichkeiten der Stapelmuster I und II nahe der von HG-Monoschichten sind, aber viel niedriger als die der Stapelmuster III und IV. Daher haben unterschiedliche Stapelmuster signifikante Auswirkungen auf die Beweglichkeit der Löcher, aber nur geringe Auswirkungen auf die Beweglichkeit der Elektronen.

Darüber hinaus wurde die Mobilität von 100 % HG neu berechnet, indem alle Elektron-Phonon-Wechselwirkungen berücksichtigt wurden, nämlich akustische Längen- (LA), transversale akustische (TA) und ZA-Phononen. Die Ergebnisse zeigen, dass die Elektronenmobilität 105 cm ² . beträgt /(V s) in K-Richtung. Abbildung 5 zeigt die Matrixelemente der Elektron-Phonon-Wechselwirkung |g | von LA-, TA- und ZA-Phononen. Es zeigt, dass die LA-Phononen bei Elektron-Phonon-Wechselwirkungen dominieren. Insgesamt haben LA-Phononen eine größere Wechselwirkungsstärke mit Elektronen als die TA- und ZA-Phononen. Obwohl der Mobilitätswert etwas niedriger ist als der nach der DPA-Methode berechnete, ist der Unterschied der beiden Methoden bei HG viel geringer als bei Arsen, Antimonen und Silicen. Im Allgemeinen ist die DPA-Methode in unserer Studie machbar.

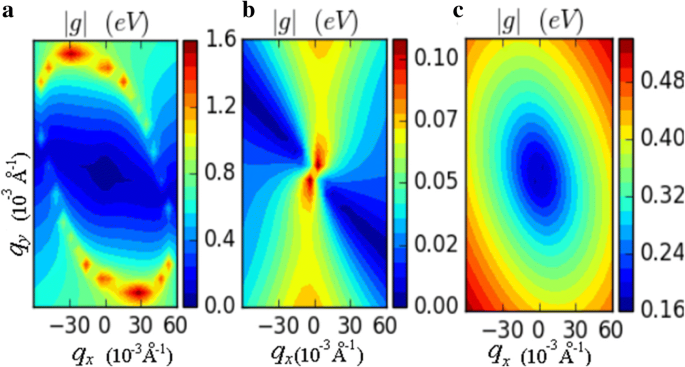
Die Matrixelemente der Elektron-Phonon-Wechselwirkung |g | von a LA, b TA und c ZA-Phononen

Schlussfolgerungen

Zusammenfassend wurden die Trägermobilitäten der HG/h-BN-Heterodoppelschicht basierend auf den First-Principles-Rechnungen in dieser Arbeit untersucht. Der Einfluss auf die Mobilitäten wird anhand der Stapelmuster der HG/h-BN-Heterodoppelschicht, der Wasserstoffbedeckung und des Hydrierungsmusters diskutiert. Der Elastizitätsmodul C _2D , effektive Masse m ^* , und Verformungspotentialkonstante E ₁ berechnet, um die Mobilitäten zu analysieren. Die Verformungspotentialkonstante weist bei den verschiedenen Mustern keine regelmäßige Tendenz auf. Der Elastizitätsmodul und die wirksame Masse in HGs sind richtungsabhängig. Die Ergebnisse zeigen, dass die ΓK-Richtung einen höheren Elastizitätsmodul hat. Die effektive Masse wird eher durch unterschiedliche Hydrierungen und Stapelmuster beeinflusst. Bei gleichem Hydrierungsmuster nimmt die Elektronenmobilität mit zunehmender Wasserstoffbedeckung monoton ab. Bei gleicher Wasserstoffbedeckung führen unterschiedliche Muster zu einer signifikanten Veränderung der Mobilitäten. Für 25 % und 6,25 % HGs beträgt der μ_e (ΓK) von 25 % Muster I ist 8985,85 cm ² /(V s) und der μ _e (ΓK) 6,25 % Muster I entspricht 23.470,98 cm ² /(V s); beide sind viel höher als die anderen Muster. Was den Einfluss des h-BN-Substrats betrifft, so beeinflussen unterschiedliche Stapelmuster die Lochbeweglichkeiten signifikant, aber kaum die Elektronenbeweglichkeiten. Die Lochbeweglichkeiten der Stapelmuster I und II sind ähnlich denen der HG-Monoschicht, aber viel niedriger als die der Stapelmuster III und IV. Insgesamt weist die HG/h-BN-Heterodoppelschicht eine beträchtliche Ladungsträgermobilität und Bandlücke unter einem spezifischen Hydrierungsmuster auf, was vielversprechende Anwendungsperspektiven in der Elektronik und Photonik bietet.

Abkürzungen

ATK:

Atomistix ToolKit

CBM:

Leitungsband-Minimum

DBG:

Direkte Bandlücke

DFT:

Dichtefunktionaltheorie

DPA:

Näherung des Verformungspotentials

FET:

Feldeffekttransistor

GGA:

Verallgemeinerte Gradienten-Approximation

h-BN:

Hexagonales Bornitrid

HG:

Hydriertes Graphen

IBG:

Indirekte Bandlücke

PBE:

Perdew-Burke-Ernzerhof

VBM:

Valenzband-Maximum

vdW:

van der Waals