Minterm vs. Maxterm-Lösung

Bisher haben wir Sum-Of-Product (SOP)-Lösungen für Logikreduktionsprobleme gefunden. Für jede dieser SOP-Lösungen gibt es auch eine Product-of-Sums-Lösung (POS), die je nach Anwendung sinnvoller sein könnte.

Bevor wir an einer Product-of-Sums-Lösung arbeiten, müssen wir einige neue Terminologien einführen. Das folgende Verfahren zum Zuordnen von Produktbegriffen ist in diesem Kapitel nicht neu.

Wir wollen nur ein formales Verfahren für Minterms zum Vergleich mit dem neuen Verfahren für Maxterms etablieren.

Minterm

Ein Minterm ist ein boolescher Ausdruck, der zu 1 . führt für die Ausgabe einer einzelnen Zelle und 0 s für alle anderen Zellen in einer Karnaugh-Karte oder Wahrheitstabelle. Wenn ein Minterm eine einzelne 1 hat und die restlichen Zellen als 0 s, es scheint eine Mindestfläche von 1 abzudecken s.

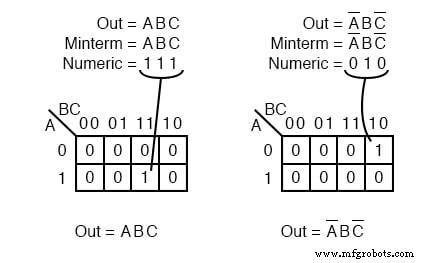
Die Abbildung oben links zeigt den Minterm ABC , ein einzelner Produktbegriff, als einzelner 1 in einer Karte, die ansonsten 0 ist S. Wir haben die 0 nicht angezeigt s in unseren Karnaugh-Karten bis zu diesem Punkt, da es üblich ist, sie wegzulassen, es sei denn, dies wird ausdrücklich benötigt. Ein weiterer Minterm A’BC’ wird oben rechts angezeigt.

Der zu überprüfende Punkt ist, dass die Adresse der Zelle direkt dem zugeordneten Minterm entspricht. Das heißt, die Zelle 111 entspricht dem Minterm ABC oben links.

Oben rechts sehen wir, dass der Minterm A’BC’ entspricht direkt der Zelle 010 . Ein boolescher Ausdruck oder eine Karte kann mehrere Minterms haben.

Unter Bezugnahme auf die obige Abbildung fassen wir das Verfahren zum Platzieren eines Minterms in einer K-Map zusammen:

• Identifizieren Sie den zuzuordnenden Minterm (Produktbegriff).
• Schreibe den entsprechenden binären numerischen Wert.
• Verwenden Sie einen Binärwert als Adresse, um eine 1 . zu platzieren in der K-Karte
• Wiederholen Sie die Schritte für andere Minterms (P-Terme innerhalb einer Summe von Produkten).

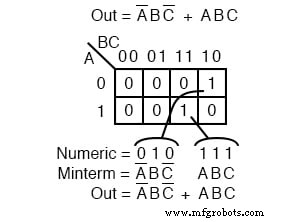
Ein boolescher Ausdruck besteht meistens aus mehreren Minterms, die mehreren Zellen in einer Karnaugh-Map entsprechen, wie oben gezeigt. Die mehreren Minterms in dieser Karte sind die einzelnen Minterms, die wir in der vorherigen Abbildung oben untersucht haben.

Der Punkt, den wir als Referenz überprüfen, ist, dass die 1 s kommen aus der K-Map als binäre Zellenadresse, die direkt in einen oder mehrere Produktbegriffe umgewandelt wird.

Mit direkt meinen wir, dass eine 0 entspricht einer komplementierten Variable und einer 1 entspricht einer wahren Variablen. Beispiel:010 konvertiert direkt in A’BC’ .

In diesem Beispiel gab es keine Reduktion. Allerdings haben wir ein Sum-Of-Products-Ergebnis aus den Minterms.

Unter Bezugnahme auf die obige Abbildung fassen wir das Verfahren zum Schreiben der Sum-Of-Products-reduzierten booleschen Gleichung aus einer K-Abbildung zusammen:

• Bilden Sie die größten Gruppen von 1 Es ist möglich, alle Minterms abzudecken. Gruppen müssen eine Potenz von 2 haben.
• Schreibe binären numerischen Wert für Gruppen.
• Binärwert in einen Produktbegriff umwandeln.
• Wiederholen Sie die Schritte für andere Gruppen. Jede Gruppe ergibt einen p-Term innerhalb einer Sum-Of-Products.

Bisher nichts Neues, ein formales Verfahren für den Umgang mit Minterms wurde festgeschrieben. Dies dient als Muster für den Umgang mit maxterms.

Als nächstes greifen wir die boolesche Funktion an, die 0 ist für eine einzelne Zelle und 1 s für alle anderen.

Maxterm

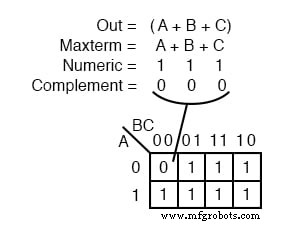
Ein maxterm ist ein boolescher Ausdruck, der zu einer 0 . führt für die Ausgabe eines einzelnen Zellenausdrucks und 1 s für alle anderen Zellen in der Karnaugh-Karte oder Wahrheitstabelle. Die Abbildung oben links zeigt den maxterm (A+B+C) , ein einzelner Summenterm, als einzelne 0 in einer Karte, die ansonsten 1 ist s.

Wenn ein Maxterm eine einzelne 0 hat und die restlichen Zellen als 1 s, es scheint eine maximale Fläche von 1 abzudecken s.

Es gibt jetzt einige Unterschiede, da wir es mit etwas Neuem zu tun haben, maxterms. Der maxterm ist eine 0 , keine 1 auf der Karnaugh-Karte. Ein maxterm ist ein Summenterm, (A+B+C) in unserem Beispiel kein Produktbegriff. Es sieht auch seltsam aus, dass (A+B+C) wird der Zelle 000 zugeordnet .

Für die Gleichung Out=(A+B+C)=0 , alle drei Variablen (A, B, C) muss individuell gleich 0 sein . Nur (0+0+0)=0 entspricht 0 . Somit setzen wir unsere einzige 0 für minterm (A+B+C) in Zelle A,B,C=000 in der K-Map, wo die Eingaben alle 0 sind .

Dies ist der einzige Fall, der uns eine 0 gibt für unsere maxterm. Alle anderen Zellen enthalten 1 s weil alle Eingabewerte außer ((0,0,0) für (A+B+C) ergibt 1 s nach Auswertung.

Mit Bezug auf die obige Abbildung ist das Verfahren zum Platzieren eines Maxterms in der K-Abbildung:

• Identifizieren Sie den zuzuordnenden Summenterm.
• Schreiben Sie den entsprechenden binären numerischen Wert.
• Bilden Sie das Komplement
• Verwenden Sie die Ergänzung als Adresse, um eine 0 . zu platzieren in der K-Karte
• Wiederholen Sie sich für andere Maxterms (Summenterme innerhalb des Product-of-Sums-Ausdrucks).

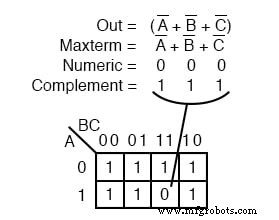
Ein weiterer maxterm A’+B’+C’ ist oben abgebildet. Numerisch 000 entspricht A’+B’+C’ . Das Komplement ist 111 . Platziere eine 0 für maxterm (A’+B’+C’) in dieser Zelle (1,1,1) der K-Map wie oben gezeigt.

Warum sollte (A’+B’+C’) eine 0 . verursachen in Zelle 111 sein ? Wenn A’+B’+C’ ist (1’+1’+1’) , alle 1 s in, das ist (0+0+0) Nachdem wir Komplemente genommen haben, haben wir die einzige Bedingung, die uns eine 0 gibt . Alle 1 s werden durch alle 0 . ergänzt s, das ist 0 wenn ODER Hrsg.

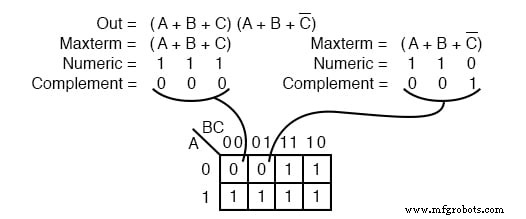
Ein boolescher Product-of-Sums-Ausdruck oder eine boolesche Zuordnung kann mehrere maxterms haben, wie oben gezeigt. Maxterm (A+B+C) ergibt numerische 111 das ergänzt 000 , Platzieren einer 0 in Zelle (0,0,0) . Maxterm (A+B+C’) ergibt numerische 110 das ergänzt 001 , Platzieren einer 0 in Zelle (0,0,1) .

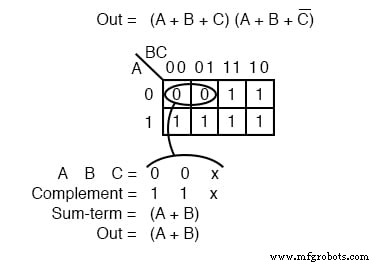
Jetzt, da wir das k-map-Setup haben, interessiert uns wirklich, wie man eine Product-of-Sums-Reduktion schreibt. Bilden Sie die 0 s in Gruppen. Das wäre eine Gruppe von zwei unten. Schreiben Sie den Binärwert, der dem Summenterm entspricht, der (0,0,X) . ist .

Sowohl A als auch B sind 0 für die Gruppe. Aber C ist beides 0 und 1 also schreiben wir ein X als Platzhalter für C . Bilden Sie das Komplement (1,1,X) . Schreiben Sie den Summenterm (A+B) das C verwerfen und das X die ihren Platz hielt.

Erwarten Sie im Allgemeinen, dass im Ergebnis des Produkts der Summen mehr Summenterme miteinander multipliziert werden. Allerdings haben wir hier ein einfaches Beispiel.

Fassen wir das Verfahren zum Schreiben der booleschen Product-of-Sums-Reduktion für eine K-Map zusammen:

• Bilden Sie die größten Gruppen von 0 s möglich und deckt alle maxterms ab. Gruppen müssen eine Potenz von 2 haben.
• Schreibe einen binären numerischen Wert für die Gruppe.
• Komplementiere den binären numerischen Wert für die Gruppe.
• Konvertieren Sie den Komplementwert in einen Summenterm.
• Wiederholen Sie die Schritte für andere Gruppen. Jede Gruppe ergibt einen Summenterm innerhalb eines Produkt-von-Summen-Ergebnisses.

Beispiele

Beispiel:

Vereinfachen Sie den booleschen Ausdruck Product-of-Sums unten, um ein Ergebnis in POS-Form bereitzustellen.

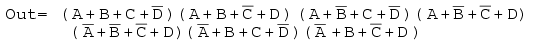
Lösung:

Übertragen Sie die sieben maxterms in die Karte unten als 0 S. Achten Sie darauf, die Eingabevariablen zu ergänzen, um die richtige Zellenposition zu finden.

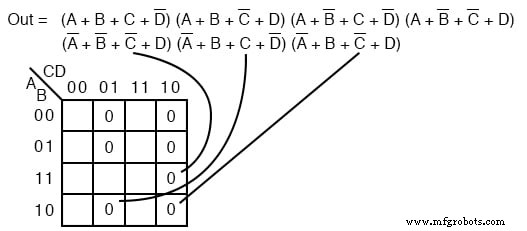
Wir kartieren die 0 s, wie sie auf der obigen Karte von links nach rechts von oben nach unten erscheinen. Wir lokalisieren die letzten drei maxterms mit Führungslinien..

Sobald die Zellen oben platziert sind, bilden Sie Gruppen von Zellen wie unten gezeigt. Größere Gruppen ergeben einen Summenterm mit weniger Eingaben. Weniger Gruppen ergeben weniger Summenterme im Ergebnis.

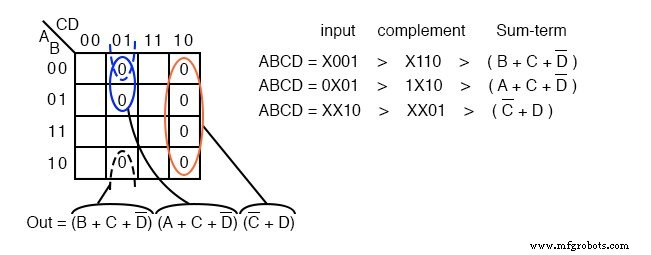
Wir haben drei Gruppen, daher erwarten wir in unserem obigen POS-Ergebnis drei Summenterme. Die Gruppe von 4 Zellen ergibt einen 2-variablen Summenterm. Die beiden Gruppen von 2-Zellen geben uns zwei 3-Variablen-Summenterme.

Details dazu, wie wir zu den Sum-Bedingungen gekommen sind, werden oben gezeigt. Schreiben Sie für eine Gruppe die binäre Gruppeneingangsadresse, ergänzen Sie sie und wandeln Sie diese in den booleschen Summenterm um. Das Endergebnis ist das Produkt der drei Summen.

Beispiel:

Vereinfachen Sie den booleschen Ausdruck Product-of-Sums unten, um ein Ergebnis in SOP-Form bereitzustellen.

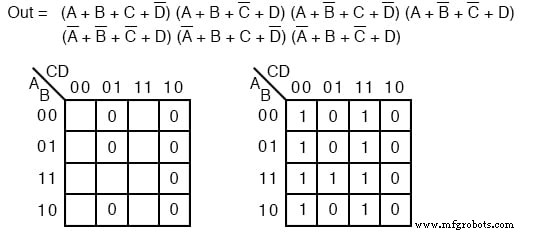
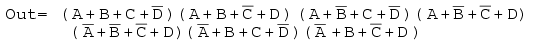
Lösung: Dies sieht aus wie eine Wiederholung des letzten Problems. Es ist nur, dass wir nach einer Sum-Of-Products-Lösung anstelle des Product-Of-Sums fragen, das wir gerade fertiggestellt haben. Maxterm 0 zuordnen s aus dem Product-Of-Sums, das wie in der vorherigen Aufgabe unten links angegeben ist.

Geben Sie dann die implizierte 1 ein s in den restlichen Zellen der Karte oben rechts.

Bilde Gruppen von 1 s, um alle 1 abzudecken S. Schreiben Sie dann das vereinfachte Ergebnis der Summe der Produkte wie im vorherigen Abschnitt dieses Kapitels. Dies ist identisch mit einem früheren Problem.

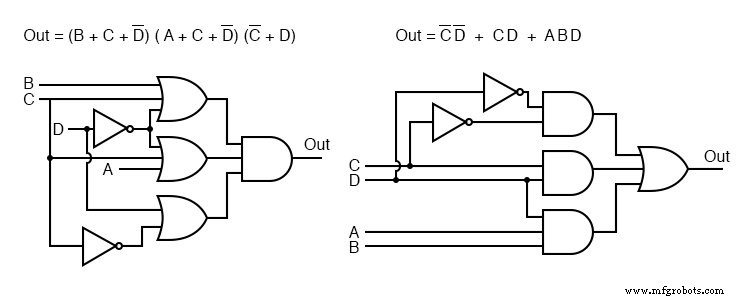
Oben zeigen wir zum Vergleich sowohl die Product-of-Sums-Lösung aus dem vorherigen Beispiel als auch die Sum-of-Products-Lösung aus dem aktuellen Problem.

Welche ist die einfachere Lösung? Der POS verwendet 3-ODER-Gatter und 1-UND-Gatter, während der SOP 3-UND-Gatter und 1-ODER-Gatter verwendet. Beide verwenden jeweils vier Tore.

Bei näherer Betrachtung zählen wir die Anzahl der Gate-Eingänge. Der POS verwendet 8 Eingänge; die SOP verwendet 7-Eingänge. Durch die Definition einer Lösung mit minimalen Kosten ist die SOP-Lösung einfacher.

Dies ist ein Beispiel für eine technisch korrekte Antwort, die in der realen Welt wenig nützt.

Die bessere Lösung hängt von der Komplexität und der verwendeten Logikfamilie ab. Die SOP-Lösung ist normalerweise besser, wenn die TTL-Logikfamilie verwendet wird, da NAND-Gatter der grundlegende Baustein sind, der gut mit SOP-Implementierungen funktioniert.

Andererseits wäre eine POS-Lösung bei Verwendung der CMOS-Logikfamilie akzeptabel, da alle Größen von NOR-Gattern verfügbar sind.

Die Gate-Diagramme für beide Fälle sind oben gezeigt, Produkt-von-Summen links und Summe-von-Produkten rechts.

Unten sehen wir uns die Sum-Of-Products-Version unserer Beispiellogik genauer an, die links wiederholt wird.

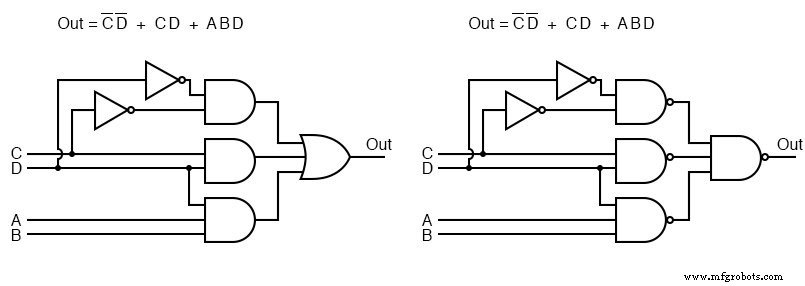
Vor allem die UND-Gatter links wurden durch NAND-Gatter rechts ersetzt. Das ODER-Gatter am Ausgang wird durch ein NAND-Gatter ersetzt. Um zu beweisen, dass die UND-ODER-Logik der NAND-NAND-Logik äquivalent ist, bewegen Sie die Umkehrblasen des Inverters am Ausgang der 3-NAND-Gatter zum Eingang des endgültigen NAND, wie in von oben rechts nach unten links gezeigt.

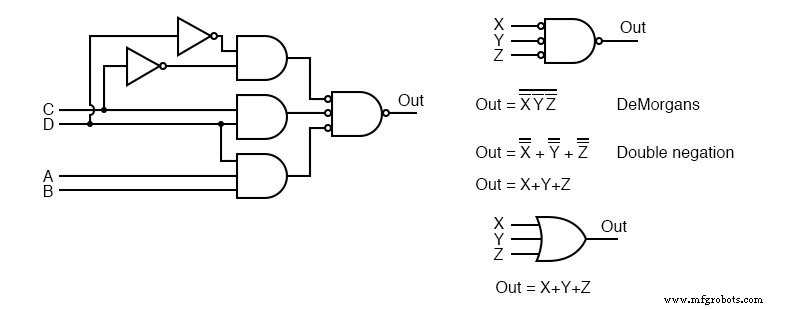
Oben rechts sehen wir, dass das Ausgangs-NAND-Gatter mit invertierten Eingängen nach DeMorgans Theorem und doppelter Negation logisch einem ODER-Gatter entspricht.

Diese Informationen sind beim Aufbau digitaler Logik in einer Laborumgebung nützlich, in der NAND-Gatter der TTL-Logikfamilie in einer Vielzahl von Konfigurationen leichter verfügbar sind als andere Typen.

Das Verfahren zum Konstruieren der NAND-NAND-Logik anstelle der UND-ODER-Logik ist wie folgt:

• Erstellen Sie ein Logikdesign mit reduzierter Summe der Produkte.
• Ersetzen Sie beim Zeichnen des Schaltplans der SOP alle Gatter (sowohl UND als auch ODER) durch NAND-Gatter.
• Nicht verwendete Eingänge sollten mit logisch High verbunden werden.
• Im Falle einer Fehlersuche stimmen interne Knoten auf der ersten Ebene der NAND-Gatter-Ausgänge NICHT mit den Logikpegeln des UND-ODER-Diagramms überein, sondern werden invertiert. Verwenden Sie das NAND-NAND-Logikdiagramm. Eingaben und Endausgabe sind jedoch identisch.
• Beschriften Sie mehrere Pakete mit U1, U2,.. usw.
• Verwenden Sie das Datenblatt, um den Ein- und Ausgängen aller Gates Pin-Nummern zuzuweisen.

Beispiel:

Lassen Sie uns ein früheres Problem erneut aufgreifen, das eine SOP-Minimierung beinhaltet. Erstellen Sie eine Product-of-Sums-Lösung. Vergleichen Sie die POS-Lösung mit der vorherigen SOP.

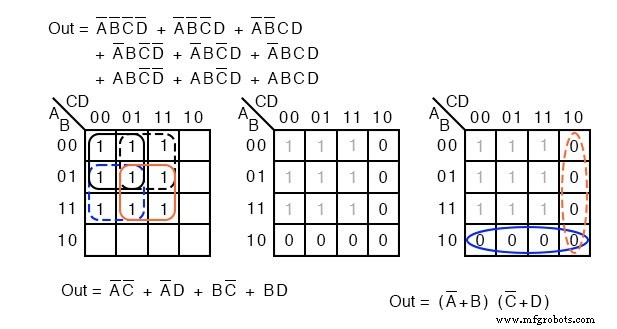
Lösung:

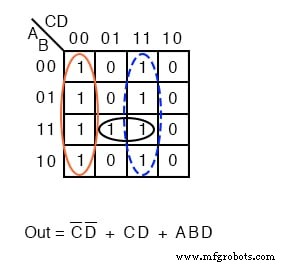
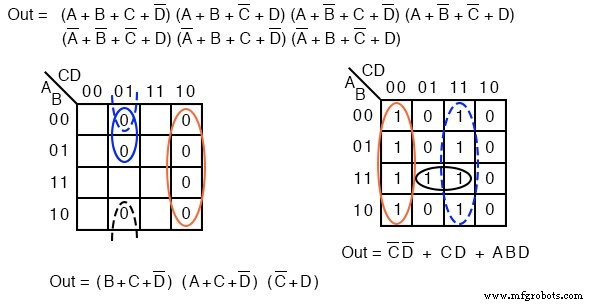
Oben links haben wir das ursprüngliche Problem, das mit einem 9-minterm-booleschen, nicht vereinfachten Ausdruck beginnt. Bei der Überprüfung bildeten wir vier Gruppen von 4 Zellen, um ein 4-Produkt-Term-SOP-Ergebnis zu erhalten, unten links.

In der mittleren Abbildung oben füllen wir die leeren Felder mit der implizierten 0 S. Die 0 s bilden zwei Gruppen von 4 Zellen. Die durchgezogene blaue Gruppe ist (A’+B) , die gestrichelte rote Gruppe ist (C’+D) . Dies ergibt zwei Summenterme im Produkt-von-Summen-Ergebnis, oben rechts Out =(A’+B)(C’+D)

Ein Vergleich der vorherigen SOP-Vereinfachung links mit der POS-Vereinfachung rechts zeigt, dass der POS die kostengünstigste Lösung ist. Die SOP verwendet insgesamt 5 Gates, die POS verwendet nur 3 Gates.

Diese POS-Lösung sieht aufgrund der Einfachheit des Ergebnisses sogar bei Verwendung von TTL-Logik attraktiv aus. Wir finden UND-Gatter und ein ODER-Gatter mit 2 Eingängen.

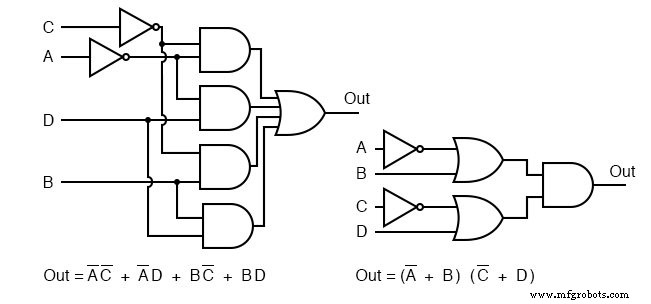
Die SOP- und POS-Gate-Diagramme sind oben für unser Vergleichsproblem gezeigt.

Angesichts der Pinbelegung für die Gatter der integrierten Schaltung der TTL-Logikfamilie unten, beschriften Sie das Maxterm-Diagramm oben rechts mit Schaltungsbezeichnungen (U1-a, U1-b, U2-a usw.) und Pin-Nummern.

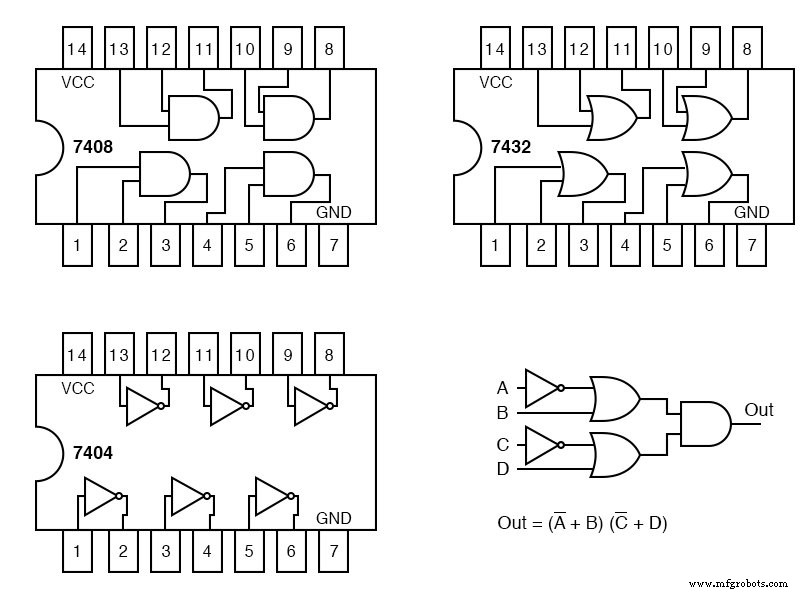
Jedes von uns verwendete integrierte Schaltungspaket erhält einen Schaltungsbezeichner:U1, U2, U3. Zur Unterscheidung der einzelnen Gates innerhalb des Pakets werden diese mit a, b, c, d usw. gekennzeichnet.

Das 7404 Hex-Inverter-Paket ist U1. Die einzelnen Inverter darin sind U1-a, U1-b, U1-c usw. U2 ist dem 7432 Quad-ODER-Gatter zugeordnet. U3 ist dem 7408 Quad-UND-Gatter zugeordnet.

Unter Bezugnahme auf die Pin-Nummern im obigen Gehäusediagramm weisen wir allen Gate-Ein- und Ausgängen im folgenden Schaltplan Pin-Nummern zu.

Wir können diese Schaltung jetzt in einer Laborumgebung aufbauen. Oder wir könnten eine Leiterplatte entwerfen dafür. Eine Leiterplatte enthält eine „Verdrahtung“ aus Kupferfolie, die von einem nicht leitfähigen Substrat aus Phenol- oder Epoxid-Glasfaser unterstützt wird.

Leiterplatten werden zur Massenproduktion elektronischer Schaltungen verwendet. Erden Sie die Eingänge nicht verwendeter Gates.

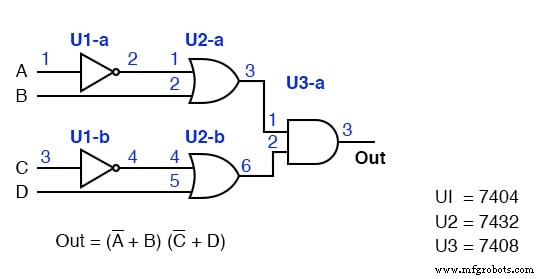
Beschriften Sie das vorherige POS-Lösungsdiagramm oben links (dritte Abbildung hinten) mit Schaltungsbezeichnungen und Pin-Nummern. Dies wird ähnlich sein, was wir gerade getan haben.

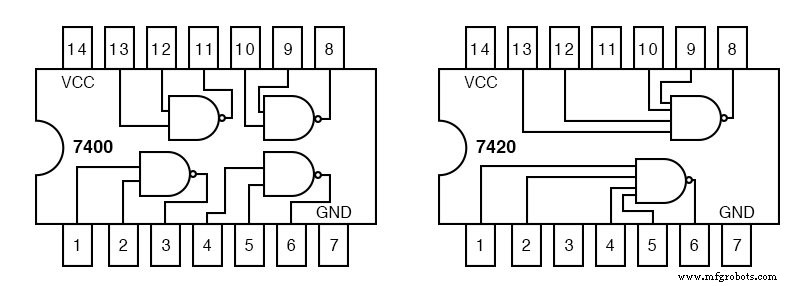
Wir finden UND-Gatter mit 2 Eingängen, 7408 im vorherigen Beispiel. Wir haben jedoch Probleme, in unserem TTL-Katalog ein ODER-Gatter mit 4 Eingängen zu finden.

Die einzige Art von Gatter mit 4 Eingängen ist das 7420 NAND-Gatter oben rechts.

Wir können das NAND-Gatter mit 4 Eingängen in ein ODER-Gatter mit 4 Eingängen verwandeln, indem wir die Eingänge des NAND-Gatters wie unten gezeigt invertieren. Wir werden also das 7420 NAND-Gatter mit 4 Eingängen als ODER-Gatter verwenden, indem wir die Eingänge invertieren.

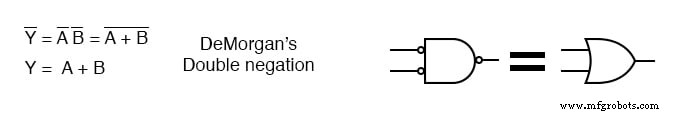
Wir werden keine diskreten Inverter verwenden, um die Eingänge des 7420 4-Eingangs-NAND-Gatters zu invertieren, sondern es mit 2-Eingangs-NAND-Gattern anstelle der UND-Gatter ansteuern, die in der SOP-Minterm-Lösung erforderlich sind.

Die Invertierung am Ausgang der NAND-Gatter mit 2 Eingängen liefert die Invertierung für das ODER-Gatter mit 4 Eingängen.

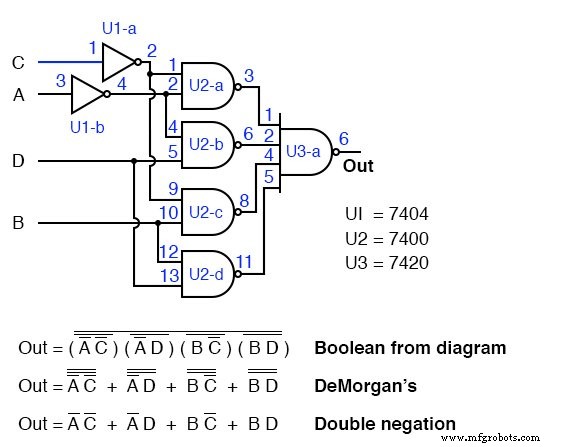
Das Ergebnis ist oben dargestellt. Es ist die einzige praktische Möglichkeit, es tatsächlich mit TTL-Gattern aufzubauen, indem die NAND-NAND-Logik verwendet wird, die die UND-ODER-Logik ersetzt.

VERWANDTE ARBEITSBLÄTTER:

• Karnaugh-Mapping-Arbeitsblatt